Deck 10: Categorical Data Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/59
Play
Full screen (f)
Deck 10: Categorical Data Analysis
1
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. As part of that analysis, a 90% confidence interval for the multinomial probability associated with the "Disagree Somewhat" response was desired. Which of the following confidence intervals should be used?
A) (0.206, 0.327)
B) (0.201, 0.332)
C) (0.225, 0.309)
D) (0.216, 0.317)
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. As part of that analysis, a 90% confidence interval for the multinomial probability associated with the "Disagree Somewhat" response was desired. Which of the following confidence intervals should be used?
A) (0.206, 0.327)
B) (0.201, 0.332)
C) (0.225, 0.309)
D) (0.216, 0.317)
(0.225, 0.309)
2
A drug company developed a honey-based liquid medicine designed to calm a child's cough at night. To test the drug, 105 children who were ill with an upper respiratory tract infection were randomly selected to participate in a clinical trial. The children were randomly divided into three groups - one group was given a dosage of the honey drug, the second was given a dosage of liquid DM (an over-the-counter cough medicine), and the third (control group) received a liquid placebo (no dosage at all). After administering the medicine to their coughing child, parents rated their children's cough diagnosis as either better or worse. The results are shown in the table below:
In order to determine whether the treatment group is independent of the coughing diagnosis, a two-way chi-square test was conducted. Use the chi-square distribution to determine the rejection region for this test when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
In order to determine whether the treatment group is independent of the coughing diagnosis, a two-way chi-square test was conducted. Use the chi-square distribution to determine the rejection region for this test when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
Reject if
3
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
Specify the null hypothesis for testing whether the true proportions of Internet users in each response category are equal.
A) , where represents the proportion of Internet users in one of the four response categories
B) , where represents the proportion of Internet users in one of the four response categories
C) , where represents the average number of Internet users in one of the found response categories
D) : Internet users and Government scanning are independent
Specify the null hypothesis for testing whether the true proportions of Internet users in each response category are equal.
A) , where represents the proportion of Internet users in one of the four response categories
B) , where represents the proportion of Internet users in one of the four response categories
C) , where represents the average number of Internet users in one of the found response categories
D) : Internet users and Government scanning are independent
, where represents the proportion of Internet users in one of the four response categories
4
The data below show the age and favorite type of music of 779 randomly selected people.
Test the claim that age and preferred music type are independent. Use
Test the claim that age and preferred music type are independent. Use

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
5
A business professor conducted a campus survey to estimate demand among all students for a protein supplement for smoothies and other nutritional drinks. Each of 113 students, randomly selected from all students on campus, provided the following information:
(1) How health conscious are you? (Very, Moderately, Slightly, Not very)
(2) Do you prefer protein supplements in your smoothies? (Yes, No)
As part of his analysis, the professor claims that whether or not the student prefers a protein supplement in smoothies is independent of health consciousness level (Very, Moderate, Slightly, or not very). Use the chi-square distribution to determine the rejection region for this test when
Testing at
A) Reject if
B) Reject if
C) Reject if
D) Reject if
(1) How health conscious are you? (Very, Moderately, Slightly, Not very)
(2) Do you prefer protein supplements in your smoothies? (Yes, No)
As part of his analysis, the professor claims that whether or not the student prefers a protein supplement in smoothies is independent of health consciousness level (Very, Moderate, Slightly, or not very). Use the chi-square distribution to determine the rejection region for this test when
Testing at
A) Reject if
B) Reject if
C) Reject if
D) Reject if

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
6
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Use the chi-square distribution to determine the rejection region when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Use the chi-square distribution to determine the rejection region when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
7
A survey of entrepreneurs focused on their job characteristics, work habits, social activities, leisure time, etc. One question put to each entrepreneur was, "What make of car (U.S., Europe, or Japan)
Do you drive?" The responses (number in each category) for a sample of 100 entrepreneurs are summarized below. The goal of the analysis is to determine if the proportions of entrepreneurs who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. Use the chi-square distribution to determine the rejection region when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
Do you drive?" The responses (number in each category) for a sample of 100 entrepreneurs are summarized below. The goal of the analysis is to determine if the proportions of entrepreneurs who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. Use the chi-square distribution to determine the rejection region when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
8
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Which of the following statements is not necessary for the analysis to be valid?
A) The expected cell counts all must be 30 or more.
B) The probabilities for the four response outcomes remain the same from one internet user to the next.
C) The 300 internet users sampled are independent from one another.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Which of the following statements is not necessary for the analysis to be valid?
A) The expected cell counts all must be 30 or more.
B) The probabilities for the four response outcomes remain the same from one internet user to the next.
C) The 300 internet users sampled are independent from one another.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
9
A survey of entrepreneurs focused on their job characteristics, work habits, social activities, leisure time, etc. One question put to each entrepreneur was, "What make of car (U.S., Europe, or Japan) do you drive?" The responses (number in each category) for a sample of 100 entrepreneurs are
Summarized below. The goal of the analysis is to determine if the proportions of entrepreneur who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)
Summarized below. The goal of the analysis is to determine if the proportions of entrepreneur who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
10
Economists at USF are researching the problem of absenteeism at U.S. firms. A random sample of 100 U.S. organizations was selected to participate in a 1-year study. As part of the study, the economists had collected data on the following two variables for each company: shiftwork available (Yes or No), and union-management relationship (Good or Poor). As part of their analyses, the economists wanted to determine whether or not a company makes shiftwork available depends on the relationship between union and management. The collected data are
Shown below:
In order to determine whether the shiftwork responses depend on the relationship responses, a two-way chi-square analysis should be conducted. Calculate the value of the test statistic for the desired analysis.
A)
B)
C)
D)
Shown below:
In order to determine whether the shiftwork responses depend on the relationship responses, a two-way chi-square analysis should be conducted. Calculate the value of the test statistic for the desired analysis.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
11
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table. In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. As part of that analysis, a 95% confidence interval for the multinomial probability associated with the "Agree Strongly" response was desired. Which of the following confidence intervals should be used?
A) (0.141, 0.259)
B) (0.162, 0.238)
C) (0.145, 0.255)
D) (0.155, 0.245)
A) (0.141, 0.259)
B) (0.162, 0.238)
C) (0.145, 0.255)
D) (0.155, 0.245)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
12
A survey of entrepreneurs focused on their job characteristics, work habits, social activities, leisure time, etc. One question put to each entrepreneur was, "What make of car (U.S., Europe, or Japan) do you drive?" The responses (number in each category) for a sample of 100 entrepreneurs are summarized below. The goal of the analysis is to determine if the proportions of entrepreneurs who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. As part of that analysis, a 95% confidence interval for the multinomial probability associated with the "Europe" response was desired. Which of the following
Confidence intervals should be used?
A) (0.257, 0.443)
B) (0.271, 0.428)
C) (0.265, 0.440)
D) (0.227, 0.473)
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. As part of that analysis, a 95% confidence interval for the multinomial probability associated with the "Europe" response was desired. Which of the following
Confidence intervals should be used?
A) (0.257, 0.443)
B) (0.271, 0.428)
C) (0.265, 0.440)
D) (0.227, 0.473)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
13
An adverse drug effect (ADE) is an unintended injury caused by prescribed medication. The table summarizes the proximal cause of 95 ADEs that resulted from a dosing error at a Boston hospital. 


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
14
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Calculate the value of the test statistic for the desired analysis.
A)
B)
C)
D)
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. Calculate the value of the test statistic for the desired analysis.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
15
A survey of entrepreneurs focused on their job characteristics, work habits, social activities, leisure time, etc. One question put to each entrepreneur was, "What make of car (U.S., Europe, or Japan)do you drive?" The responses (number in each category) for a sample of 100 entrepreneurs are summarized below. The goal of the analysis is to determine if the proportions of entrepreneurs Who drive American, European, and Japanese cars differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. Suppose the p-value for the test was calculated to be . What is the appropriate conclusion to make when testing at ?
A) There is sufficient evidence to indicate the proportion of entrepreneurs driving Japanese cars is less than the proportion driving U.S. cars.
B) There is sufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car differ.
C) There is sufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car are equal.
D) There is insufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car differ.
In order to determine whether the true proportions in each response category differ, a one-way chi-square analysis should be conducted. Suppose the p-value for the test was calculated to be . What is the appropriate conclusion to make when testing at ?
A) There is sufficient evidence to indicate the proportion of entrepreneurs driving Japanese cars is less than the proportion driving U.S. cars.
B) There is sufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car differ.
C) There is sufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car are equal.
D) There is insufficient evidence to indicate the proportion of entrepreneurs driving the three makes of car differ.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
16
A drug company developed a honey-based liquid medicine designed to calm a child's cough at night. To test the drug, 105 children who were ill with an upper respiratory tract infection were randomly selected to participate in a clinical trial. The children were randomly divided into three groups - one group was given a dosage of the honey drug, the second was given a dosage of liquid DM (an over-the-counter cough medicine), and the third (control group) received a liquid placebo (no dosage at all). After administering the medicine to their coughing child, parents rated their children's cough diagnosis as either better or worse. The results are shown in the table below:
In order to determine whether the treatment group is independent of the coughing diagnosis, a two-way chi-square test was conducted. Suppose the -value for the test was calculated to be . What is the appropriate conclusion to make when testing at ?
A) There is insufficient evidence to indicate the treatment group is dependent on the coughing diagnosis.
B) There is sufficient evidence to indicate the treatment group is independent of the coughing diagnosis.
C) There is insufficient evidence to indicate the treatment group is independent of the coughing diagnosis.
D) There is sufficient evidence to indicate the treatment group is dependent on the coughing diagnosis.
In order to determine whether the treatment group is independent of the coughing diagnosis, a two-way chi-square test was conducted. Suppose the -value for the test was calculated to be . What is the appropriate conclusion to make when testing at ?
A) There is insufficient evidence to indicate the treatment group is dependent on the coughing diagnosis.
B) There is sufficient evidence to indicate the treatment group is independent of the coughing diagnosis.
C) There is insufficient evidence to indicate the treatment group is independent of the coughing diagnosis.
D) There is sufficient evidence to indicate the treatment group is dependent on the coughing diagnosis.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
17
A business professor conducted a campus survey to estimate demand among all students for a protein supplement for smoothies and other nutritional drinks. Each of 113 students, randomly
Selected from all students on campus, provided the following information:
(1) How health conscious are you? (Very, Moderately, Slightly, Not very)
(2) Do you prefer protein supplements in your smoothies? (Yes, No)
As part of his analysis, the professor claims that whether or not the student prefers a protein
Supplement in smoothies is independent of health consciousness level (Very, Moderate, Slightly, or
Not very). Identify the appropriate alternative hypothesis that the professor should use in the test
Of hypothesis he desires.
A) : Preference and Health Consciousness level are independent variables.
B) : There is interaction between the Preference and Health Consciousness variables.
C) : Preference and Health Consciousness level are dependent variables.
D) : Preference and Health Consciousness level are mutually exclusive variables.
Selected from all students on campus, provided the following information:
(1) How health conscious are you? (Very, Moderately, Slightly, Not very)
(2) Do you prefer protein supplements in your smoothies? (Yes, No)
As part of his analysis, the professor claims that whether or not the student prefers a protein
Supplement in smoothies is independent of health consciousness level (Very, Moderate, Slightly, or
Not very). Identify the appropriate alternative hypothesis that the professor should use in the test
Of hypothesis he desires.
A) : Preference and Health Consciousness level are independent variables.
B) : There is interaction between the Preference and Health Consciousness variables.
C) : Preference and Health Consciousness level are dependent variables.
D) : Preference and Health Consciousness level are mutually exclusive variables.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
18
Inc. Technology reported the results of consumer survey in which 300 Internet users indicated their level of agreement with the following statement: "The government needs to be able to scan Internet messages and user communications to prevent fraud and other crimes." The possible responses were "agree strongly", "agree somewhat", "disagree somewhat", and "disagree strongly". The number of Internet users in each category is summarized in the table.
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)
In order to determine whether the true proportions of Internet users in each response category differ, a one-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
19
Economists at USF are researching the problem of absenteeism at U.S. firms. A random sample of 100 U.S. organizations was selected to participate in a 1-year study. As part of the study, the economists had collected data on the following two variables for each company: shiftwork available (Yes or No), and union-management relationship (Good or Poor). As part of their analyses, the economists wanted to determine whether or not a company makes shiftwork available depends on the relationship between union and management. The collected data are
Shown below:
In order to determine whether the shiftwork responses depend on the relationship responses, a two-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)
Shown below:
In order to determine whether the shiftwork responses depend on the relationship responses, a two-way chi-square analysis should be conducted. When calculating the test statistic, what values for the expected counts should be used in the calculation?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
20
Economists at USF are researching the problem of absenteeism at U.S. firms. A random sample of 100 U.S. organizations was selected to participate in a 1-year study. As part of the study, the economists had collected data on the following two variables for each company: shiftwork available (Yes or No), and union-management relationship (Good or Poor). As part of their analyses, the economists wanted to determine whether or not a company makes shiftwork available depends on the relationship between union and management. The collected data are
Shown below:
Use the chi-square distribution to determine the rejection region for this test when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if
Shown below:
Use the chi-square distribution to determine the rejection region for this test when testing at .
A) Reject if
B) Reject if
C) Reject if
D) Reject if

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
21
The contingency table below shows the results of a random sample of 200 state representatives that was conducted to see whether their opinions on a bill are related to their party affiliations.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
22
A sports researcher is interested in determining if there is a relationship between the number of home team and visiting team wins and different sports. A random sample of 526 games is selected and the results are given below. Find the rejection region used to test the claim that the number of home team and visiting team wins is independent of the sport. Use
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
23
A professor chose a random sample of 50 recent graduates of an MBA program and recorded the gender of each graduate (M or F) and whether the graduate chose to complete his or her degree requirements by completing a research project (RP) or by taking comprehensive exams (CE). The results are shown below.
a. Create a contingency table for the data.
b. Perform a -test to determine if there is any evidence that gender and choice of research project or comprehensive exams are not independent. Use .
a. Create a contingency table for the data.
b. Perform a -test to determine if there is any evidence that gender and choice of research project or comprehensive exams are not independent. Use .

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
24
A new coffeehouse wishes to see whether customers have any preference among 5 different brands of coffee. A sample of 200 customers provided the data below. Test the claim that the probabilities show no preference. Us

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
25
What is categorical data?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
26
A sports researcher is interested in determining if there is a relationship between the number of home team and visiting team wins and different sports. A random sample of 526 games is selected and the results are given below. Assuming the row and column classifications are independent, find an estimate for the expected cell count of cell
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
27
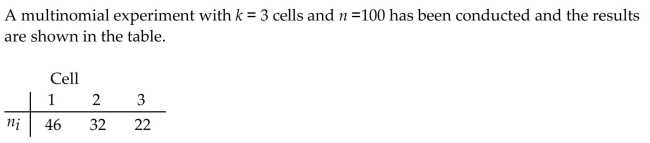 Construct a 99% confidence interval for the multinomial probability associated with cell 2.
Construct a 99% confidence interval for the multinomial probability associated with cell 2.
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the accompanying contingency table. a. Convert the values in row 1 to percentages by calculating the percentage of each column total falling in row 1.
b. Create a bar graph with row 1 percentage on the vertical axis and column number on the horizontal axis.
c. What pattern do you expect to see if the rows and columns are not independent? Is this pattern present in your graph?
b. Create a bar graph with row 1 percentage on the vertical axis and column number on the horizontal axis.
c. What pattern do you expect to see if the rows and columns are not independent? Is this pattern present in your graph?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
29
The null hypothesis for a test of data resulting from a multinomial experiment is given as 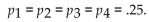 What is the alternative hypothesis for the test?
What is the alternative hypothesis for the test?
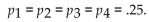 What is the alternative hypothesis for the test?
What is the alternative hypothesis for the test?
Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
30
Many track runners believe that they have a better chance of winning if they start in the inside lane that is closest to the field. For the data below, the lane closest to the field is Lane 1, the next lane is Lane 2, and so on until the outermost lane, Lane 6. The table displays the starting positions for the winners of 240 competitions. Test the claim that the probability of winning is the same regardless of starting position. Use . The results are based on 240 wins.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
31
When using any procedure to perform a hypothesis test, the user should always be certain that the
experiment satisfies the assumptions given with the procedure.
experiment satisfies the assumptions given with the procedure.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
32
A random sample of 160 car accidents are selected and categorized by the age of the driver determined to be at fault. The results are listed below. The age distribution of drivers for the given categories is 18% for the under 26 group, 39% for the 26-45 group, 31% for the 46-65 group, and 12% for the group over 65. Test the claim that all ages have crash rates proportional to their number of drivers. Use

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
33


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
34
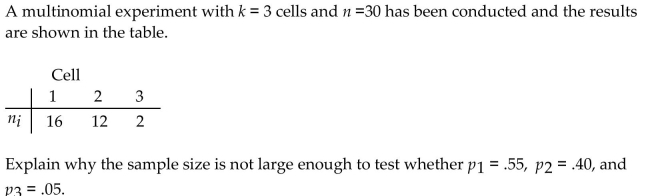

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
35
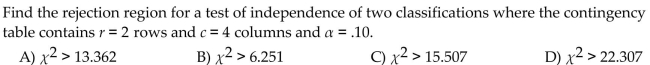

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
36


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
37
Describe probabilities of the k outcomes of the multinomial experiment trials.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
38
A teacher finds that final grades in the statistics department are distributed as: A, 25%; B, 25%; C, 40%; D, 5%; F, 5%. At the end of a randomly selected semester, the following grades were recorded. Determine if the grade distribution for the department is different than expected. Use

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
39
A sports researcher is interested in determining if there is a relationship between the
number of home team and visiting team wins and different sports. A random sample of
526 games is selected and the results are given below. Test the claim that the number of
home team and visiting team wins is independent of the sport. Use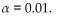

number of home team and visiting team wins and different sports. A random sample of
526 games is selected and the results are given below. Test the claim that the number of
home team and visiting team wins is independent of the sport. Use
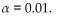


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
40
What are characteristics of the trials in a multinomial experiment?

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
41

A) 48.91
B) 37.45
C) 55.63
D) 45.91

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
42


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
43
The contingency table below shows the results of a random sample of 200 state representatives that was conducted to see whether their opinions on a bill are related to their party affiliations.
Assuming the row and column classifications are independent, find an estimate for the expected Cell count
A) 17.48
B) 27.6
C) 22.8
D) 46.92
Assuming the row and column classifications are independent, find an estimate for the expected Cell count
A) 17.48
B) 27.6
C) 22.8
D) 46.92

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
44
The contingency table below shows the results of a random sample of 200 state representatives that was conducted to see whether their opinions on a bill are related to their party affiliation. 
A) 7.662
B) 11.765
C) 9.483
D) 8.030

A) 7.662
B) 11.765
C) 9.483
D) 8.030

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
45
A random sample of 160 car accidents are selected and categorized by the age of the driver determined to be at fault. The results are listed below. The age distribution of drivers for the giver categories is for the under 26 group, for the group, for the 45 - 65 group, and for the group over 65 . Find the rejection region used to test the claim that all ages have crash rates proportional to their number of drivers. Use .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
46
Use the appropriate table to find the following probabili 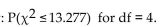
A) 0.995
B) 0.005
C) 0.010
D) 0.990
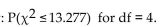
A) 0.995
B) 0.005
C) 0.010
D) 0.990

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
47

A) 2.919
B) 4.192
C) 3.290
D) 5.391

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
48
Many track runners believe that they have a better chance of winning if they start in the inside lane that is closest to the field. For the data below, the lane closest to the field is Lane 1 , the next lane is Lane 2, and so on until the outermost lane, Lane 6. The table displays the starting positions for the winners of 240 competitions. Find the rejection region used to test the claim that the probability of winning is the same regardless of starting position. Use . The results are based on 240 wins.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
49


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
50
The contingency table below shows the results of a random sample of 200 state representatives that was conducted to see whether their opinions on a bill are related to their party affiliations. Use .
Find the rejection region used to test the claim of independence.
A)
B)
C)
D)
Find the rejection region used to test the claim of independence.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
51
A teacher finds that final grades in the statistics department are distributed as: A, 25\%; B, 25\%; C, . At the end of a randomly selected semester, the following grades were recorded. Calculate the chi-square test statistic used to determine if the grade distribution for the department is different than expected. Use .
A) 6.87
B) 5.25
C) 3.41
D) 4.82
A) 6.87
B) 5.25
C) 3.41
D) 4.82

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
52
In a test of independence, it is safe to conclude that the events are independent when the value of is very small.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
53
A multinomial experiment with cells and produced the data shown in the following table.
Previous studies in this area have shown that . Construct a confidence interval for the multinomial probability associated with cell 2
A) (0.491, 0.574)
B) (0.490, 0.575)
C) (0.093, 0.157)
D) (0.484, 0.581)
Previous studies in this area have shown that . Construct a confidence interval for the multinomial probability associated with cell 2
A) (0.491, 0.574)
B) (0.490, 0.575)
C) (0.093, 0.157)
D) (0.484, 0.581)

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
54
The test for independence is a useful tool for establishing a causal relationship between two factors.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
55
Use the appropriate table to find the following
A) 7.815
B) 5.991
C) 9.488
D) 0.352
A) 7.815
B) 5.991
C) 9.488
D) 0.352

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
56


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
57
The sampling distribution for ?² works well when expected counts are very small.

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
58
A random sample of 160 car accidents are selected and categorized by the age of the driver determined to be at fault. The results are listed below. The age distribution of drivers for the given categories is for the under 26 group, for the 26-45 group, for the group, and for the group over 65 . Calculate the chi-square test statistic used to test the claim that all ages have crash rates proportional to their driving rates.
A) 85.123
B) 95.431
C) 75.101
D) 101.324
A) 85.123
B) 95.431
C) 75.101
D) 101.324

Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck
59


Unlock Deck
Unlock for access to all 59 flashcards in this deck.
Unlock Deck
k this deck


