Deck 2: Set
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/71
Play
Full screen (f)
Deck 2: Set
1
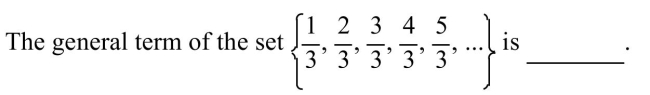
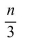
2

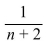
3
Which statement is false? 

C
4
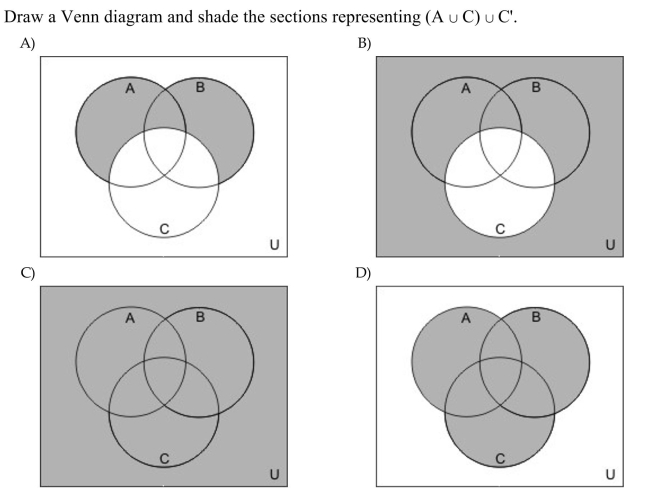

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
5
Show that the set is an infinite set. {-8, -6, -4, -2, 0, . . .}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
6
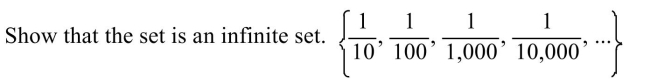

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
7
Show that the set is an infinite set. {3, 6, 9, 12, 15, . . .}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
8
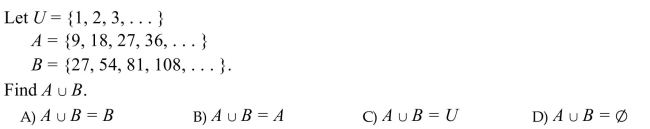

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
9
Classify each pair of sets as equal, equivalent, or neither. {1, 3, 5} and {2, 4, 6, 8}
A) equivalent
B) neither
C) equal and equivalent
A) equivalent
B) neither
C) equal and equivalent

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
10
Write the set using the descriptive method: {97, 98, 99, . . . , 110}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
11
Which statement is true? 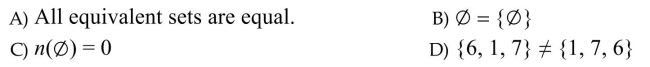
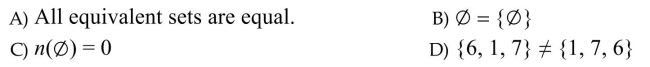

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
12
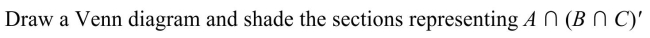

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
13
Find all subsets of the set. {2, 4, 11}.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
14
List the elements in the set: {8, 11, 14, . . . , 32}.

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
15
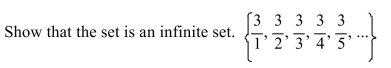

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
16
Which set is infinite? 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
17
Which set is finite? 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
18


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
19
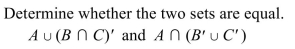

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
20


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
21


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
22
Find the number of proper subsets the set has. {m, n, p, q, r, s, t, u, v, w}
A) 1023
B) 10
C) 1022
D) 1024
A) 1023
B) 10
C) 1022
D) 1024

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
23
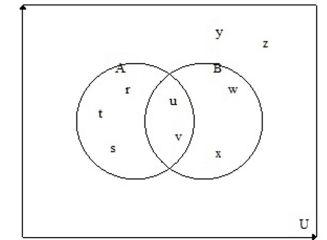
A) B? = {r, s, t}
B) B? = {r, s, t, y, z}
C) B? = {r, s, t, u, v, y, z}
D) B? = {r, s, t, u, v}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
24


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
25
Find the general term of the set. {-10, -20, -30, -40, -50, . . .}
A) -10n
B) n - 11
C) -9n - 1
D) -11n + 1
A) -10n
B) n - 11
C) -9n - 1
D) -11n + 1

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
26
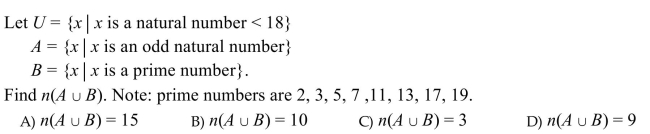

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
27
In a group of 48 children, 25 had a dog, 35 had a cat, and 15 had both a dog and a cat. How many children had neither a dog nor a cat as a pet?
A) 23
B) 20
C) 38
D) 3
A) 23
B) 20
C) 38
D) 3

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
28
Write the set using the descriptive method: {7, 14, 21, 28, 35} 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
29
A) False
B) True

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
30


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
31
Determine whether the two sets are equal. and
A) equal
B) not equal
A) equal
B) not equal

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
32
Find the cardinal number for the set. = {eleven}
A) n() = 1
B) n() = 0
C) n() = 6
D) n() = 11
A) n() = 1
B) n() = 0
C) n() = 6
D) n() = 11

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
33
State whether the collection is well-defined or not well-defined. {5, . . . }
A) Not well-defined
B) Well-defined
A) Not well-defined
B) Well-defined

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
34
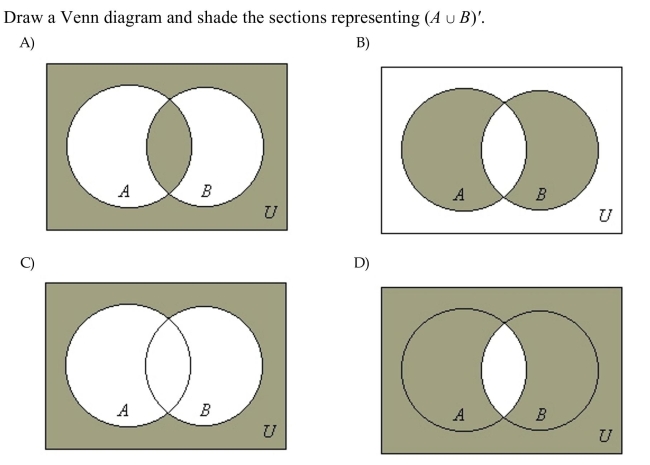

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
36
Write the set using roster notation: The set of even natural numbers less than 10. 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
37
The graph below displays the median housing prices for all houses sold in Anywhere, US between 2003 and 2008.
Median Home Prices in Anywhere
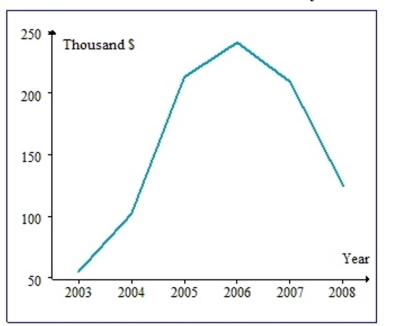
List the set of years in which the median price was above .
A) (2005, 2006, 2007, 2008}
B) (2003, 2004}
C) (2005, 2006, 2007}
D) (2003, 2004, 2008}
Median Home Prices in Anywhere

List the set of years in which the median price was above .
A) (2005, 2006, 2007, 2008}
B) (2003, 2004}
C) (2005, 2006, 2007}
D) (2003, 2004, 2008}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
38
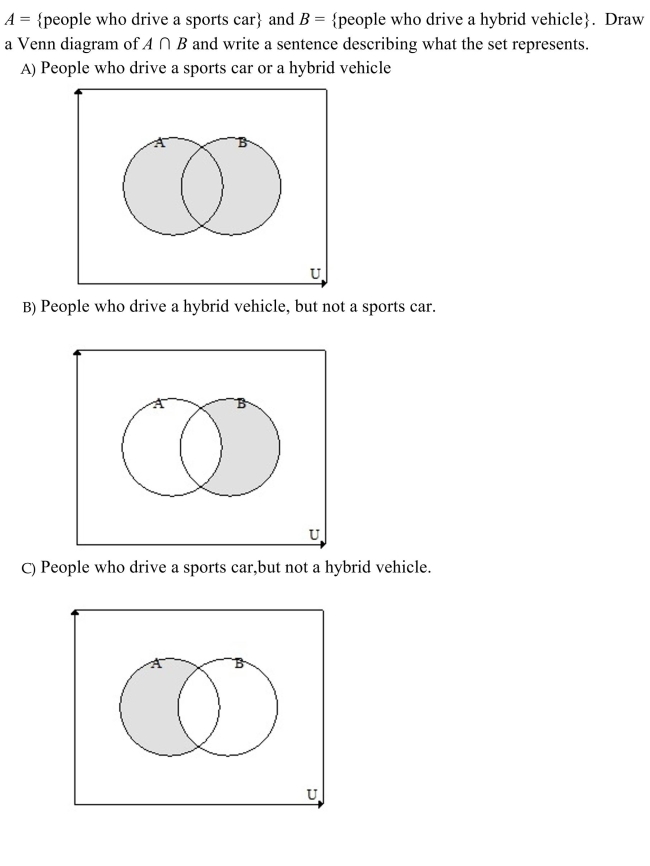
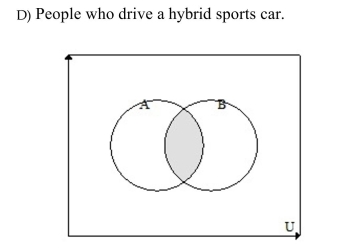

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
39
Classify each pair of sets as equal, equivalent, or neither. {a, b, c, d, e} and {5, 4, 3, 2, 1}
A) equal and equivalent
B) neither
C) equivalent
A) equal and equivalent
B) neither
C) equivalent

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
40
In a survey of 22 instructors, it was found that 5 liked whiteboards, 15 liked blackboards, and 2 liked both. How many instructors did not like whiteboards?
A) 13
B) 4
C) 19
D) 17
A) 13
B) 4
C) 19
D) 17

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
41
Let U = {3, 6, 9, 12, 15, 18, 21, 24} and A = {9, 12, 15, 21}. A' 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
42
One weekend, there were 91 pizzas ordered for the sophomore dorm. That weekend 20 customers ordered their pizza with just pepperoni, 17 customers ordered their pizza with just sausage, 10 ordered theirs with just onions, 15 ordered theirs with pepperoni and sausage, 5 ordered theirs with sausage and onions, 12 ordered theirs with pepperoni and onions, and 4 ordered theirs with all three items. The remaining pizzas were cheese pizzas with no toppings. How many customers ordered at most two toppings on their pizza?
A) 87
B) 32
C) 79
D) 26
A) 87
B) 32
C) 79
D) 26

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
43


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
44
Let X = {4, 6}. Find X × X.
A) X × X = {16, 36}
B) X × X = {16, 24, 36}
C) X × X = {(4, 4), (4, 6), (6, 4), (6, 6)}
D) X × X = {(4, 6), (6, 4)}
A) X × X = {16, 36}
B) X × X = {16, 24, 36}
C) X × X = {(4, 4), (4, 6), (6, 4), (6, 6)}
D) X × X = {(4, 6), (6, 4)}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
45
Write the set using set-builder notation: {1, 3, 5, . . . , 23} 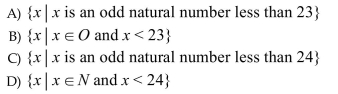
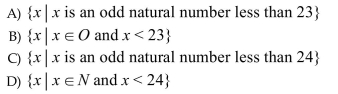

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
46
Let U = {s, t, u, v, w, x, y, z} A = {s, t, u, v} B = {s, u, w, y}. Find B - A. 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
47
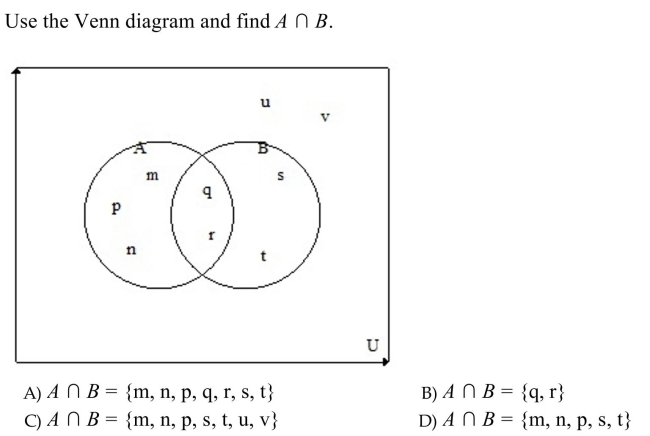

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
48
One weekend, there were 88 pizzas ordered for the sophomore dorm. That weekend 15 customers ordered their pizza with just pepperoni, 20 customers ordered their pizza with just sausage, 18 ordered theirs with just onions, 12 ordered theirs with pepperoni and sausage, 11 ordered theirs with sausage and onions, 6 ordered theirs with pepperoni and onions, and 2 ordered theirs with all three items. How many customers ordered their pizza with pepperoni or sausage (or both)?
A) 35
B) 60
C) 47
D) 10
A) 35
B) 60
C) 47
D) 10

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
49
Write the set using set-builder notation: The set of natural numbers greater than 11. 


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
50
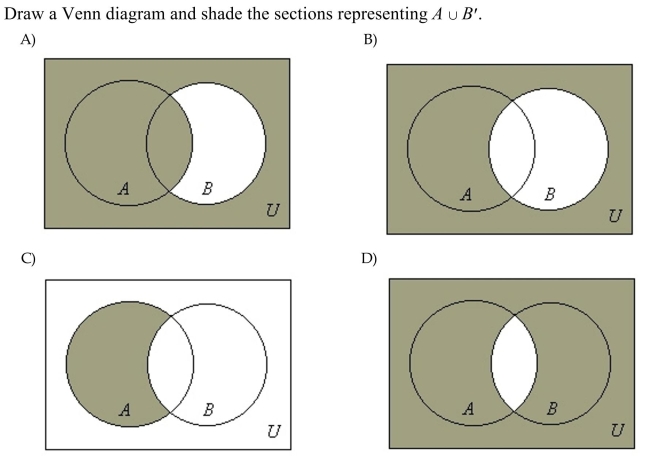

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
51


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
52
Find the general term of the set. {3, 8, 13, 18, 23, . . .}
A) 4n - 1
B) 3n
C) 5n - 2
D) 6n - 3
A) 4n - 1
B) 3n
C) 5n - 2
D) 6n - 3

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
53
Find the number of subsets the set has. {1, 2, 3, 4, 5}
A) 32
B) 31
C) 5
D) 16
A) 32
B) 31
C) 5
D) 16

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
54
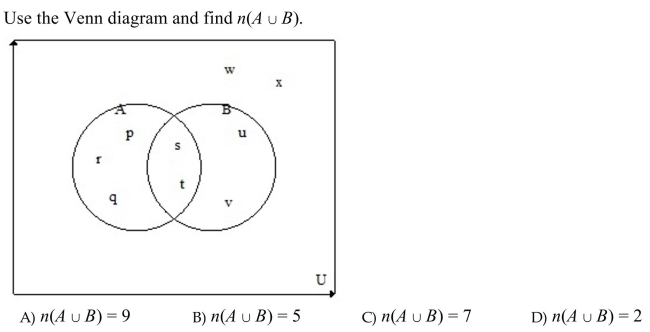

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
55
Since the student union is being remodeled, there is a limited choice of foods and drinks a student can buy for a snack between classes. Students can choose none, some, or all of these items: diet soft drink, hamburger, fries. How many different selections can be made?
A) 8
B) 9
C) 7
D) 3
A) 8
B) 9
C) 7
D) 3

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
56
Find the cardinal number for the set. = {5, 10, 15, . . . , 45}
A) n() = 9
B) n() = 45
C) The set is infinite.
D) n() = 4
A) n() = 9
B) n() = 45
C) The set is infinite.
D) n() = 4

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
57


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
58


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
59
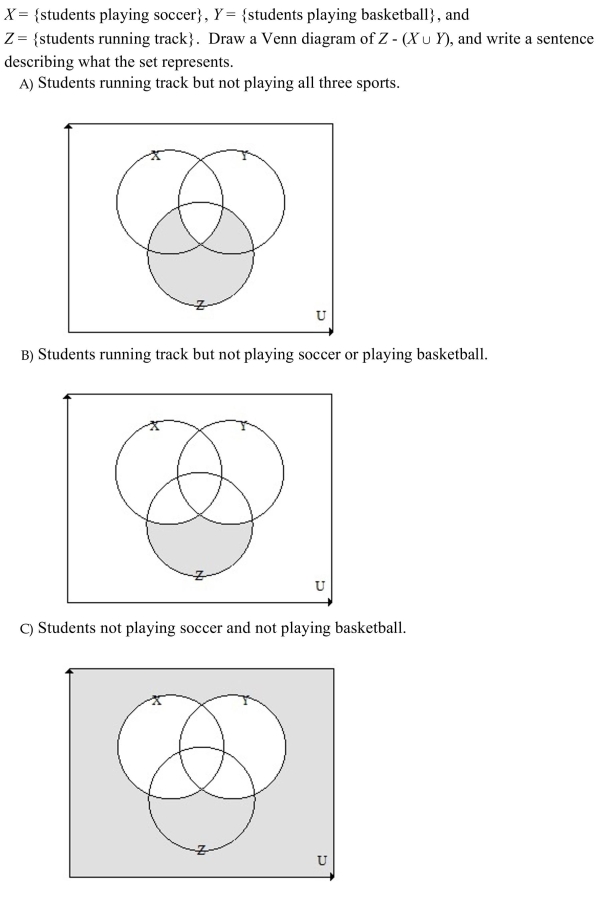
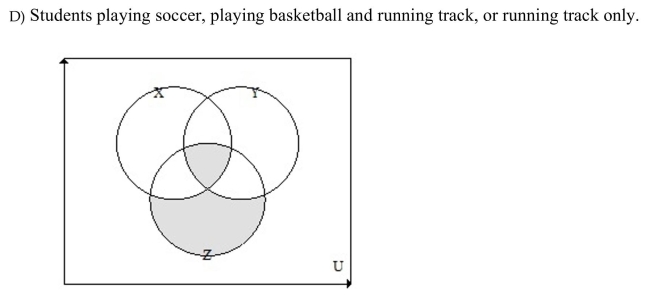

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
60
In a survey of 20 college students, it was found that 9 were taking an English class, 3 were taking a math class, and 2 were taking both English and math. How many students were taking a math class only?
A) 13
B) 11
C) 10
D) 1
A) 13
B) 11
C) 10
D) 1

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
61
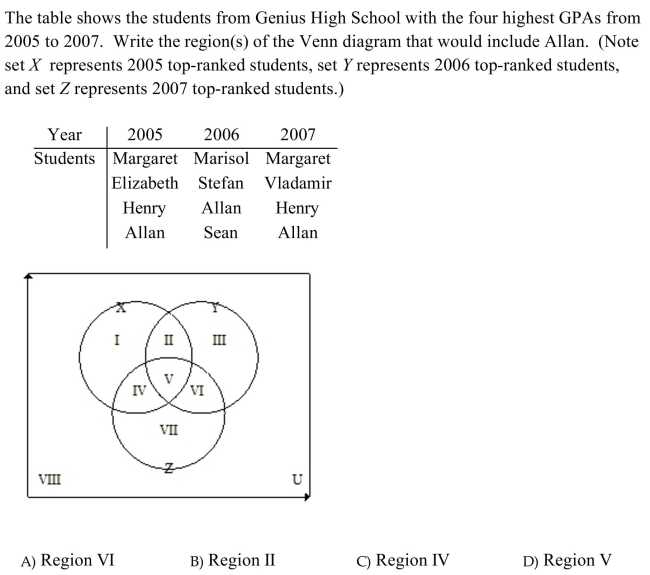

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
62
Let .
State whether the following statement true or false:
State whether the following statement true or false:

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
63
Let A = {4, 5, 6} B = {12, 16, 20}. Find B × A.
A) B × A = {(4, 12), (4, 16), (4, 20), (5, 12), (5, 16), (5, 20), (6, 12), (6, 16), (6, 20)}
B) B × A = {(12, 4), (12, 5), (12, 6), (16, 4), (16, 5), (16, 6), (20, 4), (20, 5), (20, 6)}
C) B × A = {48, 60, 72, 64, 80, 96, 80, 100, 120}
D) B × A = {48, 80, 120}
A) B × A = {(4, 12), (4, 16), (4, 20), (5, 12), (5, 16), (5, 20), (6, 12), (6, 16), (6, 20)}
B) B × A = {(12, 4), (12, 5), (12, 6), (16, 4), (16, 5), (16, 6), (20, 4), (20, 5), (20, 6)}
C) B × A = {48, 60, 72, 64, 80, 96, 80, 100, 120}
D) B × A = {48, 80, 120}

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
64
Classify each pair of sets as equal, equivalent, or neither. {1, 2, 3, . . ., 10} and {10, 9, 8, . . ., 1}
A) equal and equivalent
B) neither
C) equivalent
A) equal and equivalent
B) neither
C) equivalent

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
65
Upon examining the contents of 38 backpacks, it was found that 23 contained a black pen, 27 contained a blue pen, and 21 contained a pencil, 15 contained both a black pen and a blue pen, 12 contained both a black pen and a pencil, 18 contained both a blue pen and a pencil, and 10 contained all three items. How many backpacks contained exactly two of the three writing instruments?
A) 15
B) 11
C) 3
D) 2
A) 15
B) 11
C) 3
D) 2

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
66
Upon examining the contents of 38 backpacks, it was found that 23 contained a black pen, 27 contained a blue pen, and 21 contained a pencil, 15 contained both a black pen and a blue pen, 12 contained both a black pen and a pencil, 18 contained both a blue pen and a pencil, and 10 contained all three items. How many backpacks contained none of the three writing instruments?
A) 11
B) 15
C) 2
D) 3
A) 11
B) 15
C) 2
D) 3

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
67
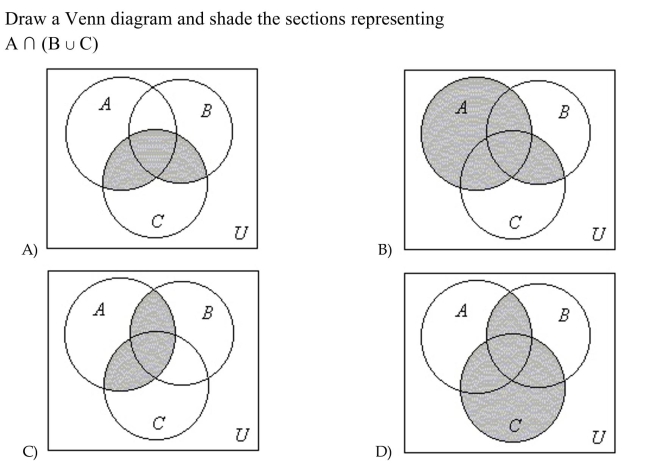

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
68


Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
69
Let U = {5, 10, 15, 20, 25, 30, 35, 40} A = {5, 10, 15, 20} B = {25, 30, 35, 40} C = {10, 20, 30, 40}. Find C'. 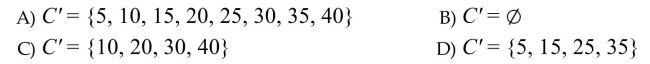
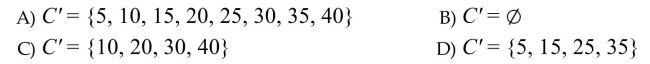

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
70
Upon examining the contents of 38 backpacks, it was found that 23 contained a black pen, 27 contained a blue pen, and 21 contained a pencil, 15 contained both a black pen and a blue pen, 12 contained both a black pen and a pencil, 18 contained both a blue pen and a pencil, and 10 contained all three items. How many backpacks contained exactly one of the three writing instruments?
A) 2
B) 3
C) 11
D) 15
A) 2
B) 3
C) 11
D) 15

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck
71
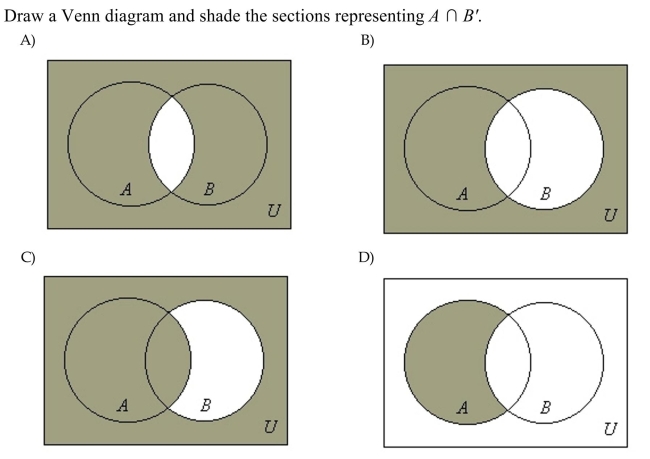

Unlock Deck
Unlock for access to all 71 flashcards in this deck.
Unlock Deck
k this deck


