Deck 3: Logic
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/80
Play
Full screen (f)
Deck 3: Logic
1
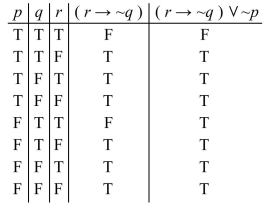
2


3
Which of the following is a simple statement?
A) February is the shortest month.
B) If you don't use sunblock, you'll get burned.
C) His eyes are neither blue nor brown.
D) He has a dog and a cat.
A) February is the shortest month.
B) If you don't use sunblock, you'll get burned.
C) His eyes are neither blue nor brown.
D) He has a dog and a cat.
A
4
Let p = "Sally is three years old." Let q = "Sally's mom is thirty." Write the following statement in words. 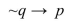
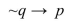

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
5


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
6
Which sentence is not a statement?
A) It's raining.
B) Jan and Ella are neighbors.
C) Who is your instructor?
D) 5 × 5 = 10
A) It's raining.
B) Jan and Ella are neighbors.
C) Who is your instructor?
D) 5 × 5 = 10

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
7


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
8
Let p = "My homework is finished." Write the following statement in symbols. It is not true that my homework is finished.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
9
Let p = "Daphne speaks Spanish." Let q = "Daphne speaks French." Write the following statement in symbols. Daphne speaks Spanish if and only if Daphne speaks French.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
10
Let p = "Ed plays the guitar." Let q = "Ed plays the piano." Write the following statement in symbols. It is false that Ed does not play the guitar or Ed plays the piano.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
11
Decide if the statement is simple or compound. I will go with you if and only if we are on time.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
12


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
13


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
14
Let p = "Paolo bicycles to school." Let q = "Roberto drives to school." Write the following statement in symbols. Paolo does not bicycle to school, or Roberto drives to school.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
15
Draw an Euler circle diagram for the statement. Some teachers are nice people.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
16
Let p = "Paolo bicycles to school." Let q = "Roberto drives to school." Write the following statement in symbols. If Paolo does not bicycle to school, then Roberto does not drive to school.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
17

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
18
Decide whether each statement is simple or compound. 


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
19


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
20
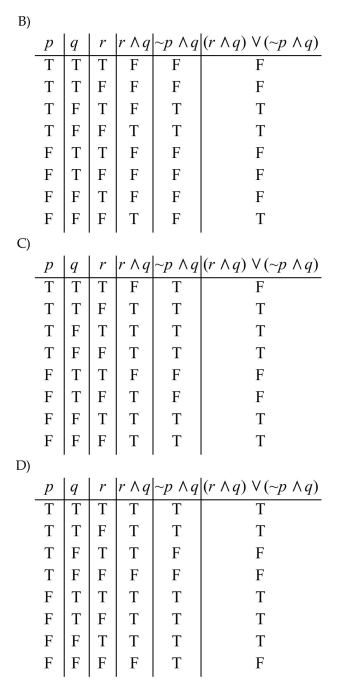
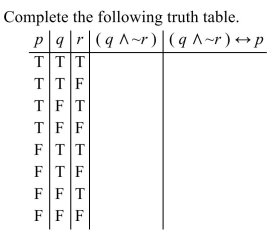
Let p = "Sally is three years old." Let q = "Sally's mom is thirty." Write the following statement in words. 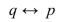
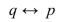

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
21
A new weight loss supplement claims that if you take this product daily and you cut your calorie intake by 10%, you will lose at least 10 pounds in the next 4 months. If you use the product daily and you don't cut your calorie intake by 10%, and then don't lose 10 pounds, is the claim made by the advertiser true or false?

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
22
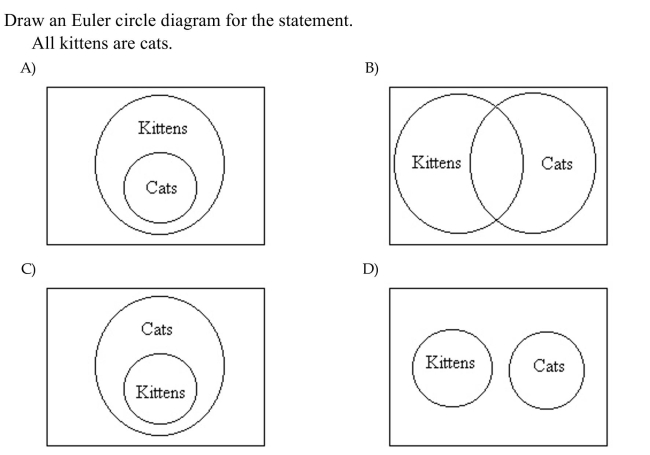

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
23
Let p = "Paolo bicycles to school." Let q = "Roberto drives to school." Write the following statement in symbols. It is not true that Paolo does not bicycle to school and Roberto does not drive to school.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
24
Determine if the two statements are logically equivalent, negations, or neither.
A) Neither
B) Logically equivalent
C) Negations
A) Neither
B) Logically equivalent
C) Negations

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
25
Write the negation of the statement. She is not angry.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
26


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
27
Is the following sentence a statement? Neither Ben nor Alonzo is going camping.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
28
Let p = "Ed plays the guitar." Let q = "Ed plays the piano." Write the following statement in symbols. Ed plays the guitar, and Ed does not play the piano.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
29
Determine whether the statement is a tautology, a self-contradiction, or neither.
A) Self-contradiction
B) Tautology
C) Neither
A) Self-contradiction
B) Tautology
C) Neither

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
30
Identify the statement as a conjunction, disjunction, conditional, or biconditional. If Jon fails this test, then he will fail the course.
A) Biconditional
B) Disjunction
C) Conditional
D) Conjunction
A) Biconditional
B) Disjunction
C) Conditional
D) Conjunction

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
31


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
32
Let p = "I am hungry." Let q = "I am going to have a snack." Write the following statement in words. 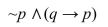
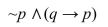

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
33
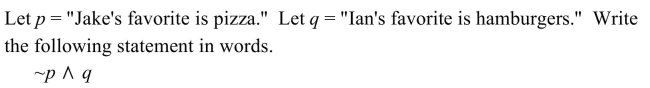

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
34
Draw an Euler circle diagram for the statement. No math classes are easy.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
36
State whether the sentence is a statement or not. Close the door.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
37


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
38


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
39


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
40
Determine whether the argument is valid or invalid. Some fizzbangers are breakdancers.
No breakdancers are jealous.
Some fizzbangers are not jealous.
A) Invalid
B) Valid
No breakdancers are jealous.
Some fizzbangers are not jealous.
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
41
Determine the validity of the following argument.
A) Valid
B) Invalid
A) Valid
B) Invalid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
42
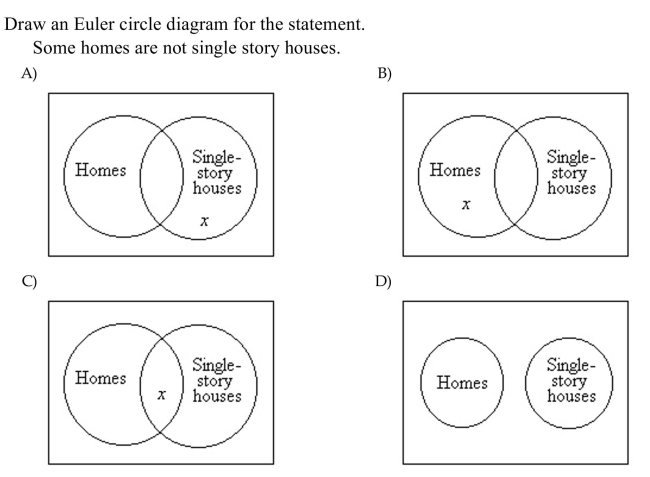

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
43
Write the negation of the statement. Everyone at my house got the flu.
A) Not everyone at my house got the flu.
B) No one at my house got the flu.
C) Someone at my house got the flu.
A) Not everyone at my house got the flu.
B) No one at my house got the flu.
C) Someone at my house got the flu.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
44


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
45
Determine whether the statement is a tautology, a self-contradiction, or neither.
A) Self-contradiction
B) Tautology
C) Neither
A) Self-contradiction
B) Tautology
C) Neither

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
46
Determine whether the following argument is valid, using the given forms of valid arguments and fallacies.
A) Valid
B) Invalid
A) Valid
B) Invalid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
47
Identify the quantifier in the statement as either universal or existential. At least one of the children was blond.
A) Universal
B) Existential
A) Universal
B) Existential

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
48
Write the converse of the conditional statement. If I get a speeding ticket, my parents do not pay for my insurance.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If my parents pay for my insurance, I do not get a speeding ticket.
C) If I get a speeding ticket, my parents pay for my insurance.
D) If I do not get a speeding ticket, my parents pay for my insurance.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If my parents pay for my insurance, I do not get a speeding ticket.
C) If I get a speeding ticket, my parents pay for my insurance.
D) If I do not get a speeding ticket, my parents pay for my insurance.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
49


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
50
Determine whether the argument is valid or invalid.
Some children are energetic.
Some children are not polite.
Some polite people are not energetic.
A) Invalid
B) Valid
Some children are energetic.
Some children are not polite.
Some polite people are not energetic.
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the argument is valid or invalid.
Some is not .
No is .
Some is not .
A) Valid
B) Invalid
Some is not .
No is .
Some is not .
A) Valid
B) Invalid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
52
Determine whether the argument is valid or invalid.
All is .
All is .
All is .
A) Invalid
B) Valid
All is .
All is .
All is .
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
53
Determine the validity of the following argument.
A) Invalid
B) Valid
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
54
Determine whether the argument is valid or invalid.
Some items are non-sale items.
No non-sale item is affordable.
Some items are not affordable.
A) Invalid
B) Valid
Some items are non-sale items.
No non-sale item is affordable.
Some items are not affordable.
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
55
Construct a truth table for the following statement.
How many T's are in the final column?
A) 2
B) 3
C) 4
D) 1
How many T's are in the final column?
A) 2
B) 3
C) 4
D) 1

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
56
A new intelligence enhancing supplement claims that if you take this product daily and you get 8 hours of sleep per night, you will increase your score by 5 points on a standard IQ test. Let p be "you take this product daily," q be "you get 8 hours of sleep per night," and r be "you will increase your score by 5 points on a standard IQ test." Write the compound statement in symbolic form, using conjunctions and the conditional. 


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
57
Determine the validity of the following argument.
A) Invalid
B) Valid
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
58
Determine whether the following argument is valid, using the given forms of valid arguments and fallacies.
A) Valid
B) Invalid
A) Valid
B) Invalid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
59
Identify the statement as a conjunction, disjunction, conditional, or biconditional. We will build a pool if and only if we win the lottery.
A) Conditional
B) Conjunction
C) Biconditional
D) Disjunction
A) Conditional
B) Conjunction
C) Biconditional
D) Disjunction

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
60
Identify the quantifier in the statement as universal or existential. Then write the negation of the statement. At least one breed of cat is hairless.
A) Existential, All breeds of cat are hairless.
B) Universal, All breeds of cat are hairless.
C) Universal, Some breeds of cat have hair.
D) Existential, No breed of cat is hairless.
A) Existential, All breeds of cat are hairless.
B) Universal, All breeds of cat are hairless.
C) Universal, Some breeds of cat have hair.
D) Existential, No breed of cat is hairless.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
61
Determine if the two statements are logically equivalent, negations, or neither.
A) Negations
B) Logically equivalent
C) Neither
A) Negations
B) Logically equivalent
C) Neither

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
62
Determine whether each sentence is a statement or not.
i.
ii. Please don't yell.
iii. She went to Spain.
iv. Kel studied for hours.
A) Yes, Yes, No, Yes
B) Yes, No, Yes, Yes
C) No, No, No, Yes
D) No, Yes, Yes, Yes
i.
ii. Please don't yell.
iii. She went to Spain.
iv. Kel studied for hours.
A) Yes, Yes, No, Yes
B) Yes, No, Yes, Yes
C) No, No, No, Yes
D) No, Yes, Yes, Yes

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
63
Determine if the two statements are logically equivalent, negations, or neither.
A) Neither
B) Negations
C) Logically equivalent
A) Neither
B) Negations
C) Logically equivalent

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
64
Determine if the two statements are logically equivalent, negations, or neither.
A) Negations
B) Neither
C) Logically equivalent
A) Negations
B) Neither
C) Logically equivalent

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
65
Write the contrapositive of the conditional statement. If I get a speeding ticket, my parents do not pay for my insurance.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If I get a speeding ticket, my parents pay for my insurance.
C) If I do not get a speeding ticket, my parents pay for my insurance.
D) If my parents pay for my insurance, I do not get a speeding ticket.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If I get a speeding ticket, my parents pay for my insurance.
C) If I do not get a speeding ticket, my parents pay for my insurance.
D) If my parents pay for my insurance, I do not get a speeding ticket.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
66
Write the converse of the conditional statement. I will buy a new computer if my laptop breaks.
A) If my laptop doesn't break, then I won't buy a new computer.
B) If I don't buy a new computer, then my laptop will break.
C) If I buy a new computer then my laptop will break
D) If I don't buy a new computer, then my laptop won't break.
A) If my laptop doesn't break, then I won't buy a new computer.
B) If I don't buy a new computer, then my laptop will break.
C) If I buy a new computer then my laptop will break
D) If I don't buy a new computer, then my laptop won't break.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
67


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
68
Write the inverse of the conditional statement. If I get a speeding ticket, my parents do not pay for my insurance.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If I get a speeding ticket, my parents pay for my insurance.
C) If I do not get a speeding ticket, my parents pay for my insurance.
D) If my parents pay for my insurance, I do not get a speeding ticket.
A) If my parents do not pay for my insurance, I get a speeding ticket.
B) If I get a speeding ticket, my parents pay for my insurance.
C) If I do not get a speeding ticket, my parents pay for my insurance.
D) If my parents pay for my insurance, I do not get a speeding ticket.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
69
Use De Morgan's laws to write the negation of the statement. The towel is wet or it isn't striped.
A) The towel is not wet and it is striped.
B) The towel is not wet or it is striped.
C) The towel is not wet or it isn't striped.
D) The towel is not wet and it isn't striped.
A) The towel is not wet and it is striped.
B) The towel is not wet or it is striped.
C) The towel is not wet or it isn't striped.
D) The towel is not wet and it isn't striped.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
70
Determine whether the statement is a tautology, a self-contradiction, or neither.
A) Tautology
B) Neither
C) Self-contradiction
A) Tautology
B) Neither
C) Self-contradiction

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
71


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
72
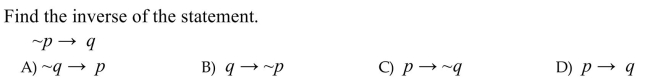

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
73
Determine whether the following argument is valid, using the given forms of valid arguments and fallacies.
A) Valid
B) Invalid
A) Valid
B) Invalid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
74
Determine if the two statements are logically equivalent, negations, or neither.
A) Neither
B) Logically equivalent
C) Negations
A) Neither
B) Logically equivalent
C) Negations

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
75
Use De Morgan's laws to write the negation of the statement. The towel is wet and it isn't striped.
A) The towel is not wet or it is striped.
B) The towel is not wet or it isn't striped.
C) The towel is not wet and it isn't striped.
D) The towel is not wet and it is striped.
A) The towel is not wet or it is striped.
B) The towel is not wet or it isn't striped.
C) The towel is not wet and it isn't striped.
D) The towel is not wet and it is striped.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
76
Write the contrapositive of the conditional statement. I will buy a new computer if my laptop breaks.
A) If my laptop doesn't break, then I won't buy a new computer.
B) If I don't buy a new computer, then my laptop won't break.
C) If I don't buy a new computer, then my laptop will break.
D) If I buy a new computer then my laptop will break
A) If my laptop doesn't break, then I won't buy a new computer.
B) If I don't buy a new computer, then my laptop won't break.
C) If I don't buy a new computer, then my laptop will break.
D) If I buy a new computer then my laptop will break

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
77
Classify each statement as simple or compound.
i. Jeff's brother is two years old.
ii. is over six feet tall.
iii. His parents own two houses.
iv. He likes cats and dogs.
A) Simple, Simple, Simple, Compound
B) Compound, Simple, Compound, Simple
C) Simple, Compound, Simple, Compound
D) Compound, Simple, Simple, Simple
i. Jeff's brother is two years old.
ii. is over six feet tall.
iii. His parents own two houses.
iv. He likes cats and dogs.
A) Simple, Simple, Simple, Compound
B) Compound, Simple, Compound, Simple
C) Simple, Compound, Simple, Compound
D) Compound, Simple, Simple, Simple

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
78
Determine the validity of the following argument.
A) Invalid
B) Valid
A) Invalid
B) Valid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
79
Write the negation of the statement. It is not true that my mother is from outer space
A) My mother is from outer space.
B) My mother is not from outer space.
C) It is true that my mother is not from outer space.
A) My mother is from outer space.
B) My mother is not from outer space.
C) It is true that my mother is not from outer space.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
80
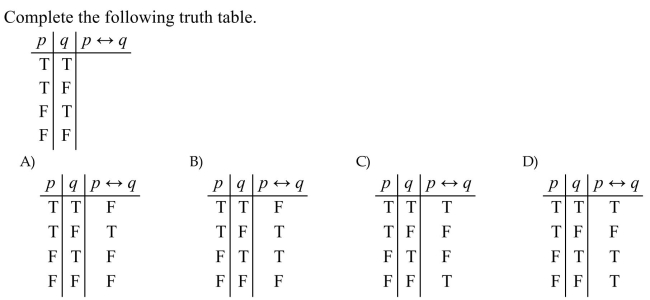

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck


