Deck 1: Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/425
Play
Full screen (f)
Deck 1: Equations and Inequalities
1
Graph the equation.
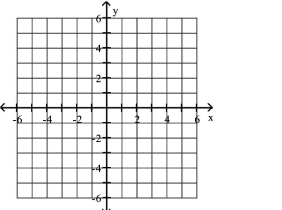
A)
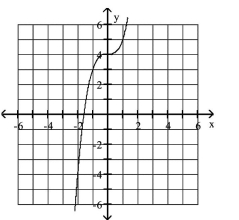
B)
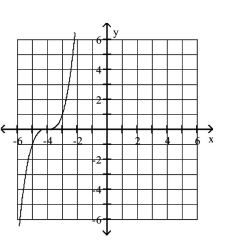
C)
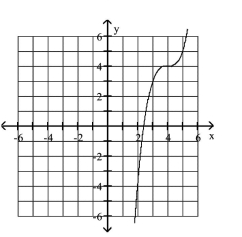
D)
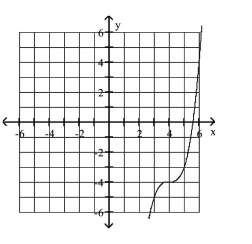

A)

B)

C)

D)

A
2
Plot the given point in a rectangular coordinate system
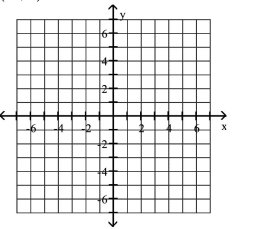
A)
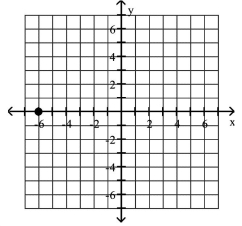
B)
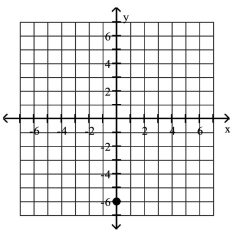
C)
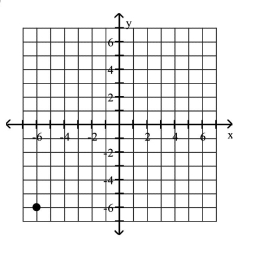
D)
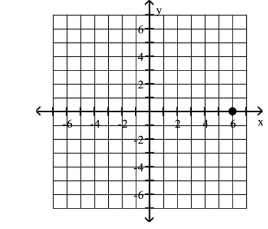

A)

B)

C)

D)

A
3
Plot the given point in a rectangular coordinate system
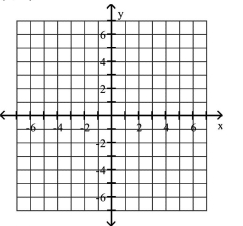
A)
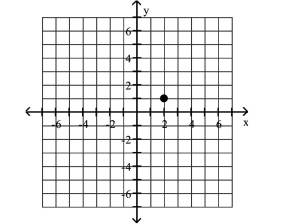
B)
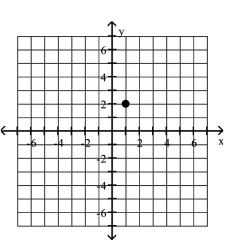
C)
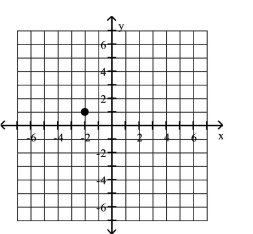
D)
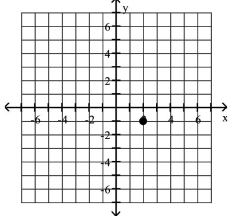

A)

B)

C)

D)

A
4
Graph the equation.
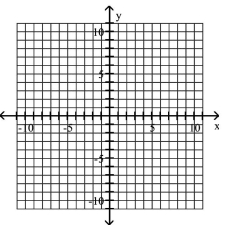
A)
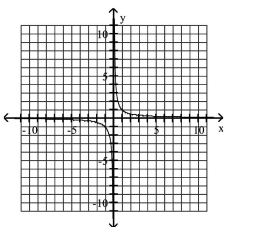
B)
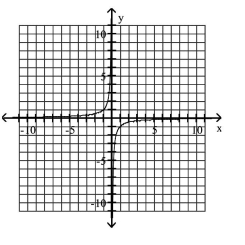
C)
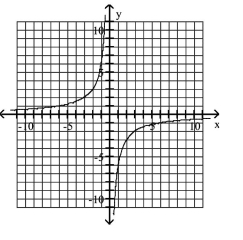
D)
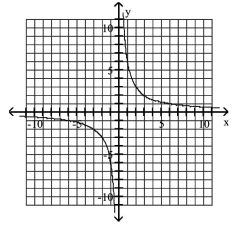
Write the English sentence as an equation in two variables. Then graph the equation.

A)

B)

C)

D)

Write the English sentence as an equation in two variables. Then graph the equation.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
5
Interpret Information About a Graphing Utility's Viewing Rectangle or Table
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 10,10,2 ] by [ - 10,10,2 ] B) [ - 2,2,2 ] by [ - 2,2,2 ] C) [ - 20,10,2 ] by [ - 20,10,2 ] D) [ - 10,10,4 ] by [ - 10,10,4 ]](https://storage.examlex.com/TB7044/11ecb7e3_e08c_68b8_b9c9_4bf0d9344334_TB7044_00.jpg)
A) by
B) by
C) by
D) by
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 10,10,2 ] by [ - 10,10,2 ] B) [ - 2,2,2 ] by [ - 2,2,2 ] C) [ - 20,10,2 ] by [ - 20,10,2 ] D) [ - 10,10,4 ] by [ - 10,10,4 ]](https://storage.examlex.com/TB7044/11ecb7e3_e08c_68b8_b9c9_4bf0d9344334_TB7044_00.jpg)
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the equation.
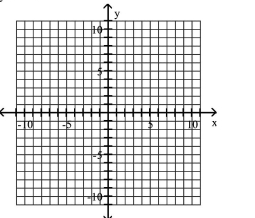
A)
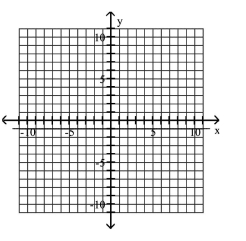
B)
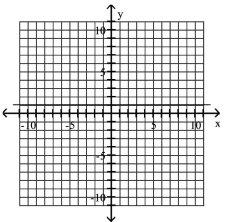
C)
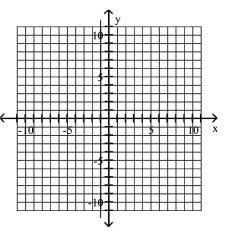
D)

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
7
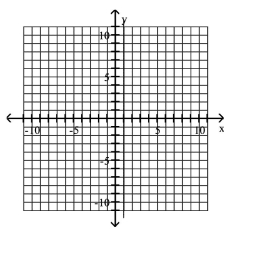
Graph the equation.
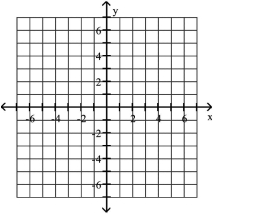
A)
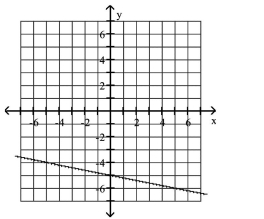
B)
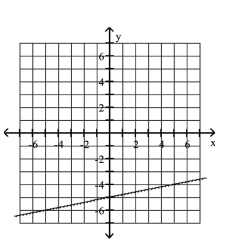
C)
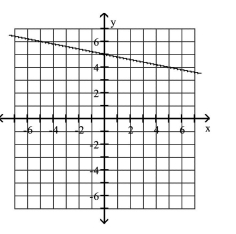
D)
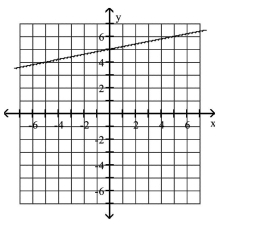

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
8
Graph the equation.
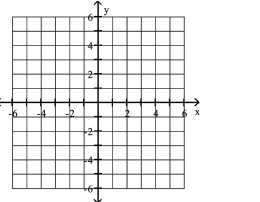
A)
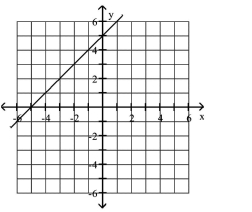
B)
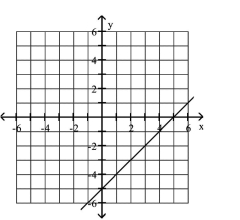
C)
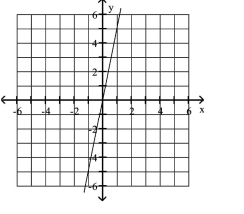
D)
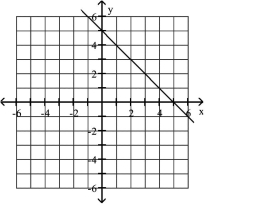

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the equation.
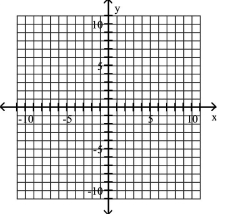
A)
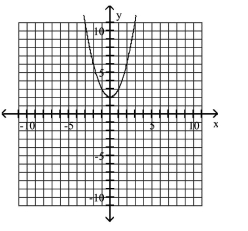
B)
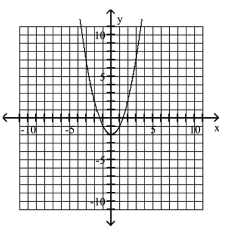
C)
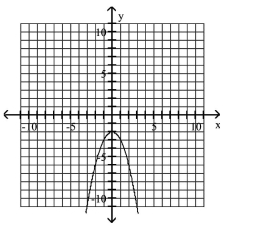
D)
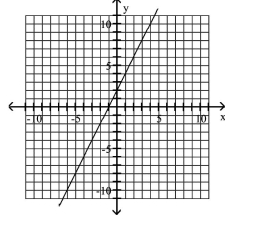

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
10
Plot the given point in a rectangular coordinate system
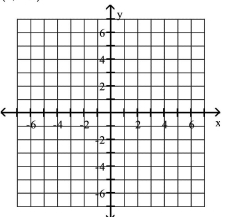
A)
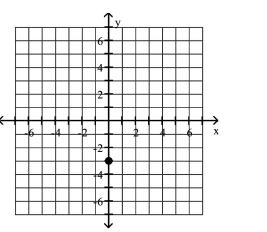
B)
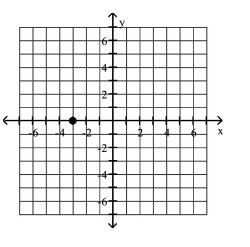
C)
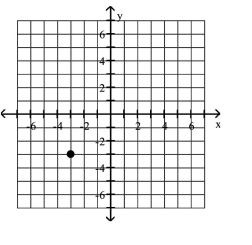
D)

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
11
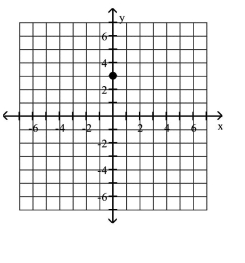
Plot the given point in a rectangular coordinate system
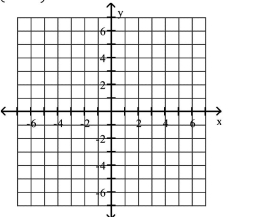
A)
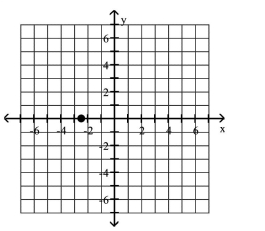
B)
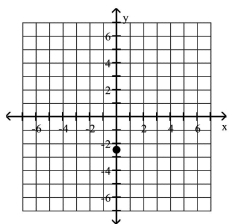
C)
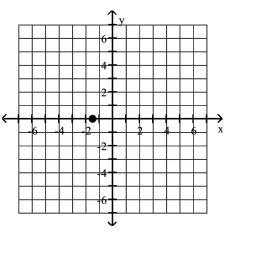
D)
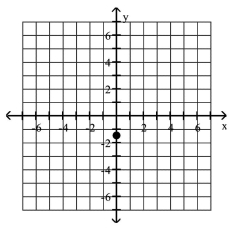

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
12
Plot the given point in a rectangular coordinate system
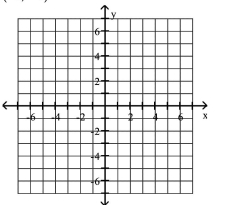
A)
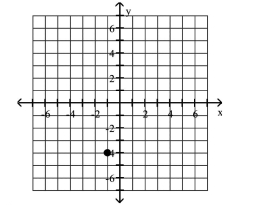
B)
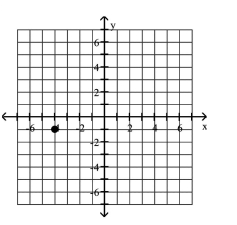
C)
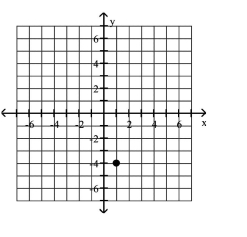
D)
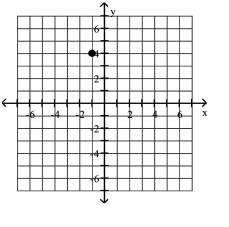

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the equation.
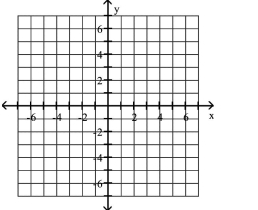
A)
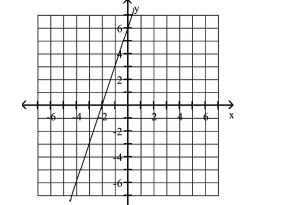
B)
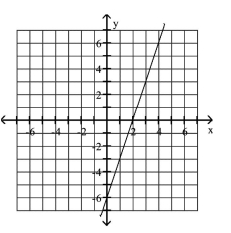
C)
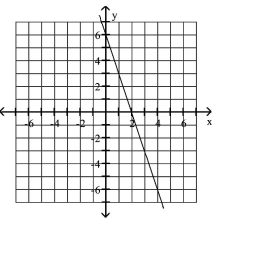
D)
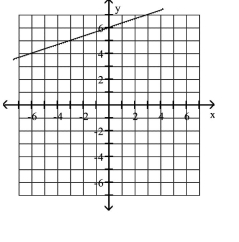

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the equation.
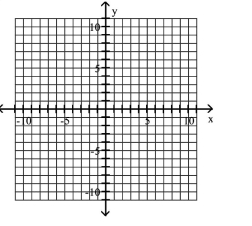
A)
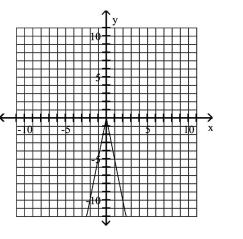
B)
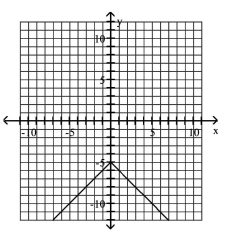
C)
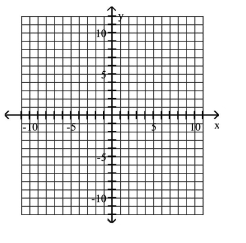
D)

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
15
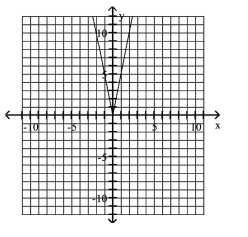
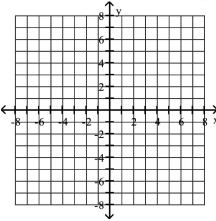
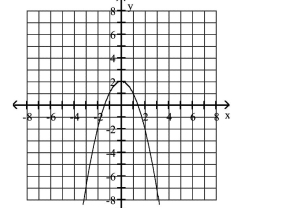
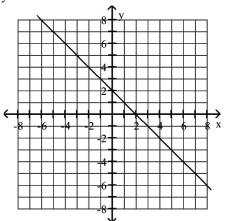
Graph the equation.
The -value is two decreased by the square of the -value.
A)
B)
C)
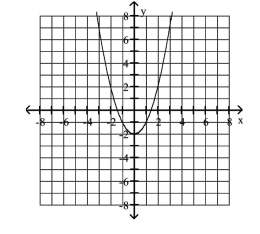
D)
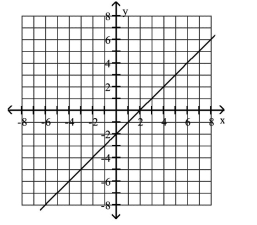
The -value is two decreased by the square of the -value.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
16
Plot the given point in a rectangular coordinate system
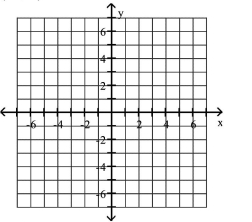
A)
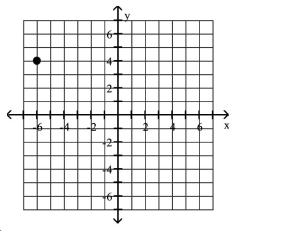
B)
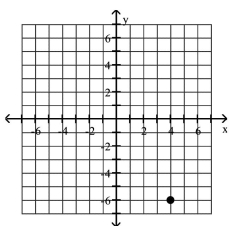
C)
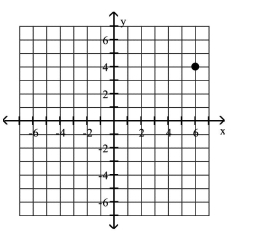
D)
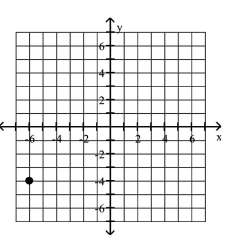

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
17
Graph the equation.
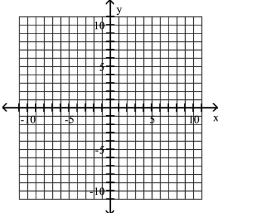
A)
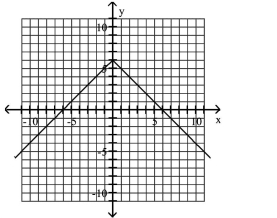
B)
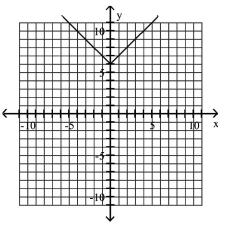
C)
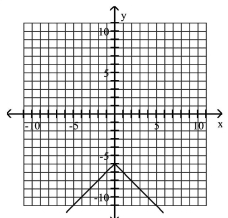
D)
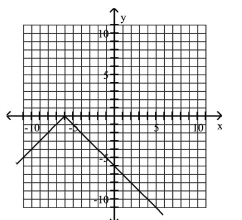

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
18
Plot the given point in a rectangular coordinate system
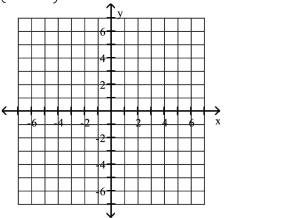
A)
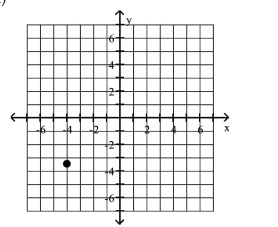
B)
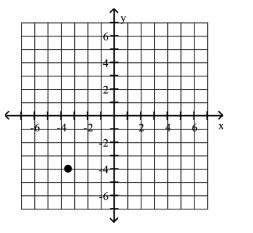
C)
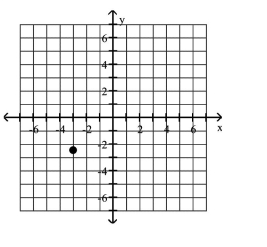
D)
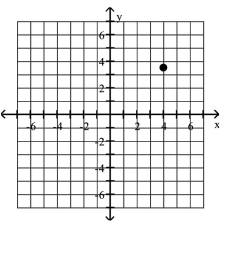

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
19
Graph the equation.
The -value is three more than five times the -value.
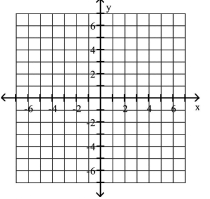
A)
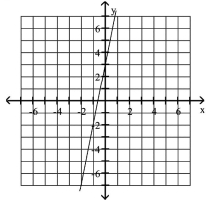
B)
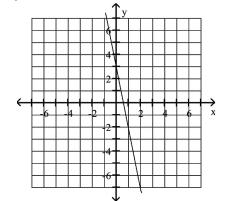
C)
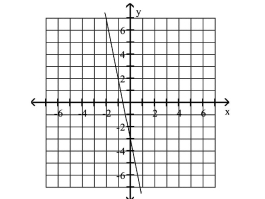
D)
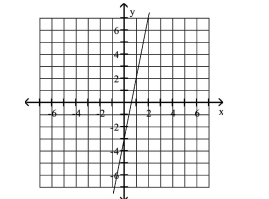
The -value is three more than five times the -value.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
20
Plot the given point in a rectangular coordinate system
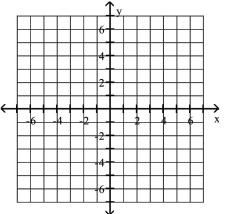
A)
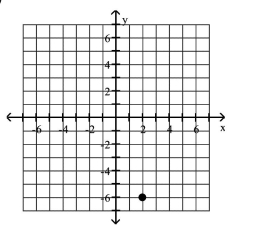
B)
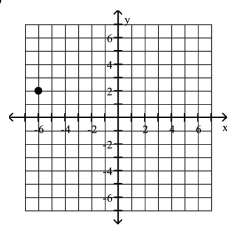
C)
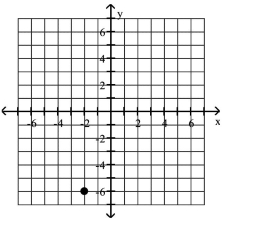
D)
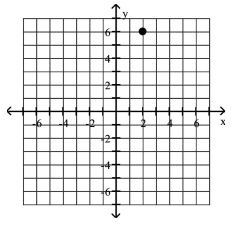

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
21
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
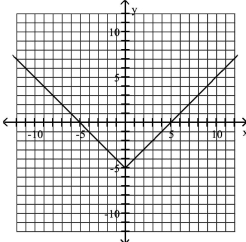
A) x-intercepts: ; y-intercept:
B) -intercepts:
C) -intercept:
D) x-intercepts: ; y-intercept: 0
Use the graph to determine the x- and y-intercepts.

A) x-intercepts: ; y-intercept:
B) -intercepts:
C) -intercept:
D) x-intercepts: ; y-intercept: 0

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
22
Interpret Information About a Graphing Utility's Viewing Rectangle or Table
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 4,4,2 ] by [ - 80,80,8 ] B) [ - 16,16,4 ] by [ - 4,4,2 ] C) [ - 4,4,2 ] by [ - 4,4,2 ] D) [ - 20,20,2 ] by [ - 20,20,2 ]](https://storage.examlex.com/TB7044/11ecb7e3_efa6_ae5a_b9c9_dfb4518dbde3_TB7044_00.jpg)
A) by
B) by
C) by
D) by
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 4,4,2 ] by [ - 80,80,8 ] B) [ - 16,16,4 ] by [ - 4,4,2 ] C) [ - 4,4,2 ] by [ - 4,4,2 ] D) [ - 20,20,2 ] by [ - 20,20,2 ]](https://storage.examlex.com/TB7044/11ecb7e3_efa6_ae5a_b9c9_dfb4518dbde3_TB7044_00.jpg)
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
23
Interpret Information About a Graphing Utility's Viewing Rectangle or Table
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 10,30,10 ] by [ - 400,500,100 ] B) [ - 1,8,1 ] by [ - 1,8,1 ] C) [ - 1,5,1 ] by [ - 4,8,1 ] D) [ - 10,5,1 ] by [ - 10,5,1 ]](https://storage.examlex.com/TB7044/11ecb7e3_f853_71fb_b9c9_37ace16e9fef_TB7044_00.jpg)
A) by
B) by
C) by
D) by
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 10,30,10 ] by [ - 400,500,100 ] B) [ - 1,8,1 ] by [ - 1,8,1 ] C) [ - 1,5,1 ] by [ - 4,8,1 ] D) [ - 10,5,1 ] by [ - 10,5,1 ]](https://storage.examlex.com/TB7044/11ecb7e3_f853_71fb_b9c9_37ace16e9fef_TB7044_00.jpg)
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
24
The table of values was generated by a graphing utility with a TABLE feature. Use the following table to solve.
At which points do the graph of and intersect?
A) and
B) and
C) and
D) and
At which points do the graph of and intersect?
A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
25
Interpret Information About a Graphing Utility's Viewing Rectangle or Table
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 1,8,1 ] by [ - 4,5,1 ] B) [ - 1,8,1 ] by [ - 1,8,1 ] C) [ - 4,5,1 ] by [ - 1,8,1 ] D) [ - 10,5,1 ] by [ - 10,5,1 ]](https://storage.examlex.com/TB7044/11ecb7e3_e841_37c9_b9c9_e9b93814112c_TB7044_00.jpg)
A) by
B) by
C) by
D) by
Match the correct viewing rectangle dimensions with the figure.
![<strong>Interpret Information About a Graphing Utility's Viewing Rectangle or Table Match the correct viewing rectangle dimensions with the figure. </strong> A) [ - 1,8,1 ] by [ - 4,5,1 ] B) [ - 1,8,1 ] by [ - 1,8,1 ] C) [ - 4,5,1 ] by [ - 1,8,1 ] D) [ - 10,5,1 ] by [ - 10,5,1 ]](https://storage.examlex.com/TB7044/11ecb7e3_e841_37c9_b9c9_e9b93814112c_TB7044_00.jpg)
A) by
B) by
C) by
D) by

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
26
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
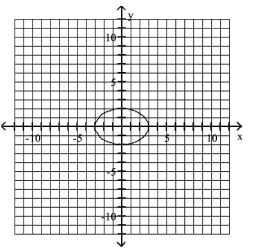
A) -intercepts: -intercepts:
B) -intercepts:
C) -intercepts:
D) -intercepts: -intercepts:
Use the graph to determine the x- and y-intercepts.

A) -intercepts: -intercepts:
B) -intercepts:
C) -intercepts:
D) -intercepts: -intercepts:

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
27
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.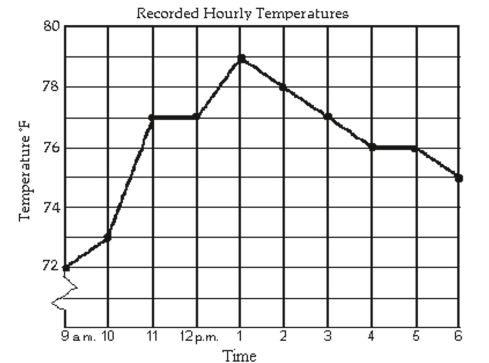
During which hour did the temperature increase the most?
A) 10 a.m. to 11 a.m.
B) 1 p.m. to 2 p.m.
C) 12 p.m. to 1 p.m.
D) 9 a.m. to 10 a.m.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

During which hour did the temperature increase the most?
A) 10 a.m. to 11 a.m.
B) 1 p.m. to 2 p.m.
C) 12 p.m. to 1 p.m.
D) 9 a.m. to 10 a.m.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
28
The table of values was generated by a graphing utility with a TABLE feature. Use the following table to solve.
Does the graph of pass through the origin?
A)
B) Yes
Does the graph of pass through the origin?
A)
B) Yes

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
29
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
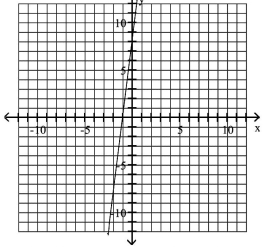
A) -intercept: ; -intercept: 8
B) -intercept: 1 ; -intercept: 8
C) x-intercept: -intercept:
D) -intercept: -intercept: 8
Use the graph to determine the x- and y-intercepts.

A) -intercept: ; -intercept: 8
B) -intercept: 1 ; -intercept: 8
C) x-intercept: -intercept:
D) -intercept: -intercept: 8

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
30
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.
At what time was the temperature the highest?
A) 1 p.m.
B) 5 p.m.
C) .
D) 2 p.m.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

At what time was the temperature the highest?
A) 1 p.m.
B) 5 p.m.
C) .
D) 2 p.m.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
31
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.
What temperature was recorded at 3 p.m.?
A)
B)
C)
D)
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

What temperature was recorded at 3 p.m.?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
32
The table of values was generated by a graphing utility with a TABLE feature. Use the following table to solve.
For which values of is ?
A) and 3
B) and 3
C) and
D) and 0
For which values of is ?
A) and 3
B) and 3
C) and
D) and 0

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
33
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
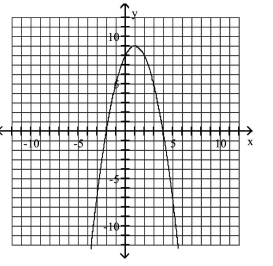
A) -intercepts: -intercept: 8
B) -intercept: -intercepts: 4,8
C) -intercept: -intercepts:
D) -intercept: -intercept: 8
Use the graph to determine the x- and y-intercepts.

A) -intercepts: -intercept: 8
B) -intercept: -intercepts: 4,8
C) -intercept: -intercepts:
D) -intercept: -intercept: 8

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
34
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.
During which two hour period did the temperature increase the most?
A) 9 a.m. to 11 a.m.
B) 10 a.m. to 11 a.m.
C) 12 p.m. to 2 p.m.
D) 10 a.m. to 12 p.m.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

During which two hour period did the temperature increase the most?
A) 9 a.m. to 11 a.m.
B) 10 a.m. to 11 a.m.
C) 12 p.m. to 2 p.m.
D) 10 a.m. to 12 p.m.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
35
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
A) -intercept:
B) -intercept:
C) x-intercept: 1
D) -intercept: 1
Use the graph to determine the x- and y-intercepts.

A) -intercept:
B) -intercept:
C) x-intercept: 1
D) -intercept: 1

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
36
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.
At what time was the temperature ?
A) 10 a.m.
B) 4 p.m. and 5 p.m.
C) 5 p.m.
D) 10 a.m. and 11 a.m.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

At what time was the temperature ?
A) 10 a.m.
B) 4 p.m. and 5 p.m.
C) 5 p.m.
D) 10 a.m. and 11 a.m.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
37
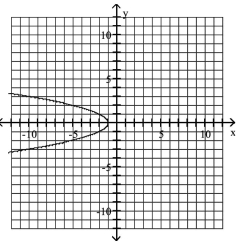
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
A) -intercepts: -intercept:
B) -intercept: -intercepts:
C) x-intercepts: -intercept:
D) -intercept: -intercepts:
Use the graph to determine the x- and y-intercepts.

A) -intercepts: -intercept:
B) -intercept: -intercepts:
C) x-intercepts: -intercept:
D) -intercept: -intercepts:

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
38
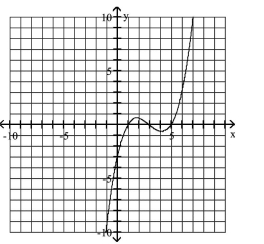
Use a Graph to Determine Intercepts
Use the graph to determine the x- and y-intercepts.
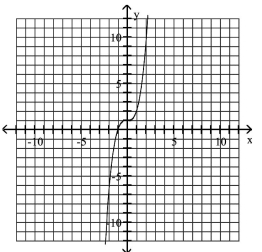
A) x-intercept: ; y-intercept: 1
B) x-intercept: ; y-intercept:
C) -intercept: 1 ; -intercept: 1
D) -intercept: -intercept:
Use the graph to determine the x- and y-intercepts.

A) x-intercept: ; y-intercept: 1
B) x-intercept: ; y-intercept:
C) -intercept: 1 ; -intercept: 1
D) -intercept: -intercept:

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
39
The table of values was generated by a graphing utility with a TABLE feature. Use the following table to solve.
Which equation corresponds to in the table?
A)
B)
C)
D)
Which equation corresponds to in the table?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
40
Choose the one alternative that best completes the statement or answers the question.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.
At what time was the temperature its lowest?
A) 9 a.m.
B) 6 p.m.
C) 4 p.m.
D) 1 p.m.
The line graph shows the recorded hourly temperatures in degrees Fahrenheit at an airport.

At what time was the temperature its lowest?
A) 9 a.m.
B) 6 p.m.
C) 4 p.m.
D) 1 p.m.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
42
Match the story with the correct figure.
The height of an animal as a function of time.
A)
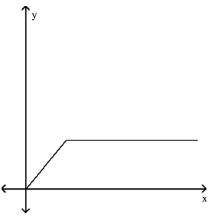
B)
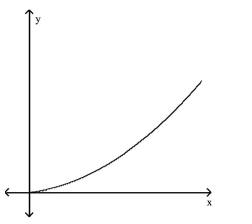
C)
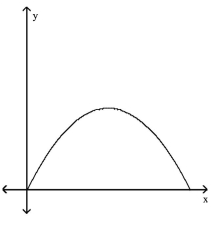
D)
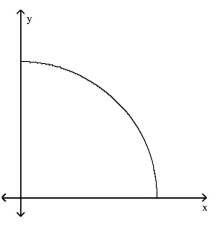
The height of an animal as a function of time.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
44
Solve and check the linear equation.
A)
B)
C)
D) Find all values of x satisfying the given conditions.
A)
B)
C)
D) Find all values of x satisfying the given conditions.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
45
Match the story with the correct figure.
The amount of rainfall as a function of time, if the rain fell more and more softly.
A)
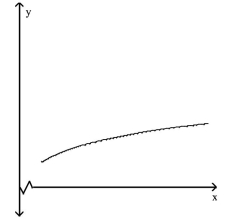
B)
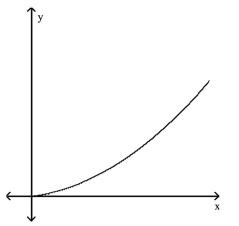
C)
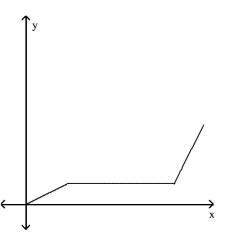
D)
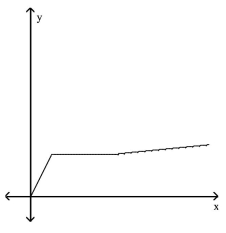
The amount of rainfall as a function of time, if the rain fell more and more softly.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
46
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
47
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
48
Solve and check the linear equation.
, and
A)
B)
C)
D) Find all values of x such that y = 0.
, and
A)
B)
C)
D) Find all values of x such that y = 0.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
50
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
51
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
52
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
53
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the equation.
A)
B)
C) 0
D)
A)
B)
C) 0
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
56
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
57
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
58
Solve and check the linear equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
59
Match the story with the correct figure.
Mark started out by walking up a hill for 5 minutes. For the next 5 minutes he walked down a steep hill to an elevation lower than his starting point. For the next 10 minutes he walked on level ground. For the next 10 minutes he walked uphill. Determine which graph of elevation above sea level versus time illustrates the story.
A)
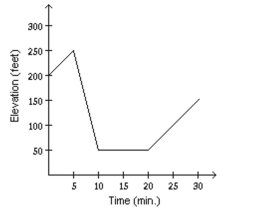
B)
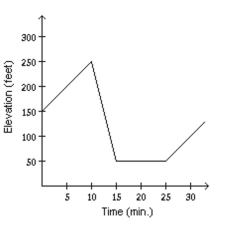
C)
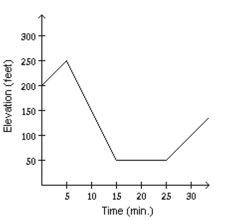
D)
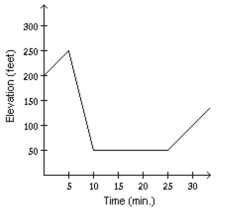
Mark started out by walking up a hill for 5 minutes. For the next 5 minutes he walked down a steep hill to an elevation lower than his starting point. For the next 10 minutes he walked on level ground. For the next 10 minutes he walked uphill. Determine which graph of elevation above sea level versus time illustrates the story.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
61
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D) No restrictions;
A)
B)
C)
D) No restrictions;

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
62
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
, and
A)
B)
C)
D)
, and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
63
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
64
Determine whether the equation is an identity, a conditional equation, or an inconsistent equation.
A) Identity
B) Conditional equation
C) Inconsistent equation
A) Identity
B) Conditional equation
C) Inconsistent equation

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
65
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
66
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
67
Determine whether the equation is an identity, a conditional equation, or an inconsistent equation.
A) Identity
B) Conditional equation
C) Inconsistent equation
A) Identity
B) Conditional equation
C) Inconsistent equation

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the equation.
A)
B)
C)
D) Find all values of x satisfying the given conditions.
A)
B)
C)
D) Find all values of x satisfying the given conditions.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the equation.
, and
A)
B)
C)
D) Find all values of x such that y = 0.
, and
A)
B)
C)
D) Find all values of x such that y = 0.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
71
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
, and
A)
B)
C)
D)
, and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
72
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D) No restrictions;
A)
B)
C)
D) No restrictions;

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
73
Determine whether the equation is an identity, a conditional equation, or an inconsistent equation.
A) Identity
B) Conditional equation
C) Inconsistent equation
A) Identity
B) Conditional equation
C) Inconsistent equation

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
74
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D) No restrictions; Solve the equation.
A)
B)
C)
D) No restrictions; Solve the equation.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
75
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D) Find all values of x satisfying the given conditions.
A)
B)
C)
D) Find all values of x satisfying the given conditions.

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
76
Determine whether the equation is an identity, a conditional equation, or an inconsistent equation.
A) Identity
B) Conditional equation
C) Inconsistent equation
A) Identity
B) Conditional equation
C) Inconsistent equation

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
77
Determine whether the equation is an identity, a conditional equation, or an inconsistent equation.
A) Identity
B) Conditional equation
C) Inconsistent equation
A) Identity
B) Conditional equation
C) Inconsistent equation

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
78
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
79
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck
80
First, write the value(s) that make the denominator(s) zero. Then solve the equation.
A)
B)
C)
D) No restrictions;
A)
B)
C)
D) No restrictions;

Unlock Deck
Unlock for access to all 425 flashcards in this deck.
Unlock Deck
k this deck


