Deck 8: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/288
Play
Full screen (f)
Deck 8: Systems of Equations and Inequalities
1
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)
A
2
Determine whether the given ordered pair is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution
A
3
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)
A
4
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the given ordered pair is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
6
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the given ordered pair is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
8
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
9
Solve Linear Systems by Addition
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
10
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the given ordered pair is a solution of the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the given ordered pair is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
13
Determine whether the given ordered pair is a solution of the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
14
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
15
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether the given ordered pair is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
17
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
18
Determine whether the given ordered pair is a solution of the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
19
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
20
Solve Linear Systems by Substitution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
21
Solve Linear Systems by Addition
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
22
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D) )
A)
B)
C)
D) )

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
23
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
24
Solve Linear Systems by Addition
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
25
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
26
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
27
Solve Linear Systems by Addition
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
28
Solve Linear Systems by Addition
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
29
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
30
Solve Linear Systems by Addition
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
31
Solve Linear Systems by Addition
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
32
Solve Linear Systems by Addition
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
33
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
34
Solve Linear Systems by Addition
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
35
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
36
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D) )
A)
B)
C)
D) )

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
37
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
38
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
39
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D) )
A)
B)
C)
D) )

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
40
Solve Linear Systems by Addition
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
41
Solve Problems Using Systems of Linear Equations
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Determine the dollar amount coming in and going out at the break-even point.
A)
B)
C)
D)
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Determine the dollar amount coming in and going out at the break-even point.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
42
Solve Problems Using Systems of Linear Equations
One number is 3 less than a second number. Twice the second number is 18 less than 5 times the first. Find the two numbers.
A) 8 and 11
B) 7 and 10
C) 9 and 12
D) and
One number is 3 less than a second number. Twice the second number is 18 less than 5 times the first. Find the two numbers.
A) 8 and 11
B) 7 and 10
C) 9 and 12
D) and

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
43
Solve Problems Using Systems of Linear Equations
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Determine the number of sold-out performances, , needed to break even.
A) 8 performances
B) 9 performances
C) 10 performances
D) 2 performances
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Determine the number of sold-out performances, , needed to break even.
A) 8 performances
B) 9 performances
C) 10 performances
D) 2 performances

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
44
Solve Problems Using Systems of Linear Equations
Is there a profit when 910 binoculars are produced?
A) Yes
B)
Is there a profit when 910 binoculars are produced?
A) Yes
B)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
45
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
46
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
47
Solve Problems Using Systems of Linear Equations
How many binoculars must be produced and sold for the company to break even?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars
How many binoculars must be produced and sold for the company to break even?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
48
Solve Problems Using Systems of Linear Equations
Use the revenue and cost functions to write the profit function from producing and selling binoculars.
A)
B)
C)
D)
Use the revenue and cost functions to write the profit function from producing and selling binoculars.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
49
Solve Problems Using Systems of Linear Equations
An-Mei owns a business making and selling jackets. She has a fixed cost of . It costs to produce each jacket. The selling price is per jacket. Let represent the number of jackets produced and sold and write the cost function, , and revenue function, .
A)
B)
C)
D)
An-Mei owns a business making and selling jackets. She has a fixed cost of . It costs to produce each jacket. The selling price is per jacket. Let represent the number of jackets produced and sold and write the cost function, , and revenue function, .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
50
Solve Problems Using Systems of Linear Equations
One number is 8 less than a second number. Twice the second number is 61 more than 5 times the first. Find the two numbers.
A) and
B) and
C) and
D) 7 and 15
One number is 8 less than a second number. Twice the second number is 61 more than 5 times the first. Find the two numbers.
A) and
B) and
C) and
D) 7 and 15

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
51
Solve Problems Using Systems of Linear Equations
What is the profit when 964 binoculars are produced?
A)
B)
C)
D)
What is the profit when 964 binoculars are produced?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
52
Solve Problems Using Systems of Linear Equations
Fewer than how many binoculars must be produced and sold for the company to have a profit loss?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars
Fewer than how many binoculars must be produced and sold for the company to have a profit loss?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
53
Solve Problems Using Systems of Linear Equations
Two cars leave a city and head in the same direction. After 7 hours, the faster car is 63 miles ahead of the slower car. The slower car has traveled 336 miles. Find the speeds of the two cars.
A) and
B) and
C) and
D) and The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question.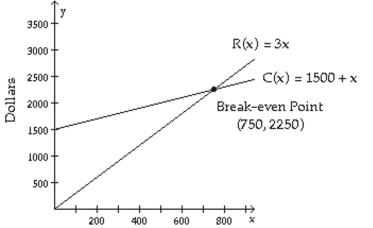
Two cars leave a city and head in the same direction. After 7 hours, the faster car is 63 miles ahead of the slower car. The slower car has traveled 336 miles. Find the speeds of the two cars.
A) and
B) and
C) and
D) and The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question.


Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
54
Solve Problems Using Systems of Linear Equations
At the break-even point both cost and revenue are what?
A)
B)
C)
D)
At the break-even point both cost and revenue are what?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
55
Solve Problems Using Systems of Linear Equations
The sum of two numbers is 9 . If one number is subtracted from the other, their difference is . Find the numbers.
A) 4,5
B)
C)
D) 6,3
The sum of two numbers is 9 . If one number is subtracted from the other, their difference is . Find the numbers.
A) 4,5
B)
C)
D) 6,3

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
56
Solve Problems Using Systems of Linear Equations
More than how many binoculars must be produced and sold for the company to have a profit gain?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars
More than how many binoculars must be produced and sold for the company to have a profit gain?
A) 750 binoculars
B) 2250 binoculars
C) 1500 binoculars
D) 2700 binoculars

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
57
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
58
Solve Problems Using Systems of Linear Equations
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Let represent the number of sold-out performances and write the cost function, and revenue function, .
A)
B)
C)
D)
Steve invests in a circus production. The cost includes an overhead of , plus production costs of per performance. A sold-out performance brings in . Let represent the number of sold-out performances and write the cost function, and revenue function, .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
59
Identify Systems That Do Not Have Exactly One Ordered-Pair Solution
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
60
Solve Problems Using Systems of Linear Equations
Is there a profit when 238 binoculars are produced?
A)
B) Yes
Is there a profit when 238 binoculars are produced?
A)
B) Yes

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
61
Solve Problems Using Systems of Linear Equations
You invested and started a business selling vases. Supplies cost per vase and you are selling each vase for . Determine the number of vases, , that must be produced and sold to break even.
A) 1800 units
B) 1801 units
C) 1802 units
D) 577 units
You invested and started a business selling vases. Supplies cost per vase and you are selling each vase for . Determine the number of vases, , that must be produced and sold to break even.
A) 1800 units
B) 1801 units
C) 1802 units
D) 577 units

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
62
Solve Problems Using Systems of Linear Equations
An-Mei owns a business making and selling jackets. She has a fixed cost of . It costs to produce each jacket. The selling price is per jacket. Determine the number of jackets that must be made and sold in order to break even.
A) 120 units
B) 121 units
C) 122 units
D) 13 units
An-Mei owns a business making and selling jackets. She has a fixed cost of . It costs to produce each jacket. The selling price is per jacket. Determine the number of jackets that must be made and sold in order to break even.
A) 120 units
B) 121 units
C) 122 units
D) 13 units

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
63
Solve Problems Using Systems of Linear Equations
Johnny's cafe serves desserts. One serving of ice cream and two servings of blueberry pie provides 800 calories. Three servings of ice cream and two servings of blueberry pie provides 1280 calories. Find the caloric content of each item.
A) Serving of ice cream: 240 calories
B) Serving of ice cream: 280 calories
Serving of blueberry pie: 280 calories Serving of blueberry pie: 240 calories
C) Serving of ice cream: 230 calories
D) Serving of ice cream: 246 calories
Serving of blueberry pie: 285 calories Serving of blueberry pie: 277 calories
Johnny's cafe serves desserts. One serving of ice cream and two servings of blueberry pie provides 800 calories. Three servings of ice cream and two servings of blueberry pie provides 1280 calories. Find the caloric content of each item.
A) Serving of ice cream: 240 calories
B) Serving of ice cream: 280 calories
Serving of blueberry pie: 280 calories Serving of blueberry pie: 240 calories
C) Serving of ice cream: 230 calories
D) Serving of ice cream: 246 calories
Serving of blueberry pie: 285 calories Serving of blueberry pie: 277 calories

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
64
Solve Problems Using Systems of Linear Equations
As the price of a product increases, the demand for that product decreases. However, at higher prices, suppliers are willing to produce greater quantities of the product. The weekly supply and demand models for a certain type of television are as follows:
Demand:
Supply:
where is the price in dollars per television.
How many of these televisions can be sold and supplied at per television?
A) sold: 210 ; supplied: 312
B) sold: 1170 ; supplied: 312
C) sold: 210 ; supplied: 1002
D) sold: 312 ; supplied: 210
As the price of a product increases, the demand for that product decreases. However, at higher prices, suppliers are willing to produce greater quantities of the product. The weekly supply and demand models for a certain type of television are as follows:
Demand:
Supply:
where is the price in dollars per television.
How many of these televisions can be sold and supplied at per television?
A) sold: 210 ; supplied: 312
B) sold: 1170 ; supplied: 312
C) sold: 210 ; supplied: 1002
D) sold: 312 ; supplied: 210

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
65
Solve Problems Using Systems of Linear Equations
A bank teller has and bills in her cash drawer. The value of the bills is . How many bills are there?
A) bills
B) bills
C) bills
D) bills
A bank teller has and bills in her cash drawer. The value of the bills is . How many bills are there?
A) bills
B) bills
C) bills
D) bills

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
66
Solve Problems Using Systems of Linear Equations
In the town of Milton Lake, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing.
Let represent the number of years since 1990 and y represent the percentage of women in Milton Lake who smoke. The graph of against includes the data points and . Let represent the number of years since 1990 and y represent the percentage of men in Milton Lake who smoke. The graph of against includes the data points and .
Determine when the percentage of women who smoke will be the same as the percentage of men who smoke. Round to the nearest year. What percentage of women and what percentage of men (to the nearest whole percent) will smoke at that time?
[Hint: first find the slope-intercept equation of the line that models the percentage, , of women who smoke x years after 1990 and the slope-intercept equation of the line that models the percentage, , of men who smoke x years after 1990]
A)
B)
C)
D)
In the town of Milton Lake, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing.
Let represent the number of years since 1990 and y represent the percentage of women in Milton Lake who smoke. The graph of against includes the data points and . Let represent the number of years since 1990 and y represent the percentage of men in Milton Lake who smoke. The graph of against includes the data points and .
Determine when the percentage of women who smoke will be the same as the percentage of men who smoke. Round to the nearest year. What percentage of women and what percentage of men (to the nearest whole percent) will smoke at that time?
[Hint: first find the slope-intercept equation of the line that models the percentage, , of women who smoke x years after 1990 and the slope-intercept equation of the line that models the percentage, , of men who smoke x years after 1990]
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
67
Solve Problems Using Systems of Linear Equations
A flat rectangular piece of aluminum has a perimeter of 70 inches. The length is 11 inches longer than the width. Find the width.
A) 12 inches
B) 23 inches
C) 34 inches
D) 35 inches
A flat rectangular piece of aluminum has a perimeter of 70 inches. The length is 11 inches longer than the width. Find the width.
A) 12 inches
B) 23 inches
C) 34 inches
D) 35 inches

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
68
Systems of Linear Equations in Three Variables
1 Verify the Solution of a System of Linear Equations in Three Variables
A) solution
B) not a solution
1 Verify the Solution of a System of Linear Equations in Three Variables
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
69
Solve Problems Using Systems of Linear Equations
You invested and started a business selling vases. Supplies cost per vase and you are selling each vase for . Let represent the number of vases produced and sold and write the cost function, , and revenue function, .
A)
B)
C)
D)
You invested and started a business selling vases. Supplies cost per vase and you are selling each vase for . Let represent the number of vases produced and sold and write the cost function, , and revenue function, .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
70
Solve Problems Using Systems of Linear Equations
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 3 bags of potato chips for . Another customer buys 2 hot dogs and 2 bags of potato chips for . Find the cost of each item.
A) for a hot dog; for a bag of potato chips
B) for a hot dog; for a bag of potato chips
C) for a hot dog; for a bag of potato chips
D) for a hot dog; for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 4 hot dogs and 3 bags of potato chips for . Another customer buys 2 hot dogs and 2 bags of potato chips for . Find the cost of each item.
A) for a hot dog; for a bag of potato chips
B) for a hot dog; for a bag of potato chips
C) for a hot dog; for a bag of potato chips
D) for a hot dog; for a bag of potato chips

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
71
Solve Problems Using Systems of Linear Equations
Julie and Eric row their boat (at a constant speed) 27 miles downstream for 3 hours, helped by the current. Rowing at the same rate, the trip back against the current takes 9 hours. Find the rate of the current.
A)
B)
C)
D)
Julie and Eric row their boat (at a constant speed) 27 miles downstream for 3 hours, helped by the current. Rowing at the same rate, the trip back against the current takes 9 hours. Find the rate of the current.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
72
Solve Problems Using Systems of Linear Equations
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is more than the value of the nickels. How many nickels and dimes does Jamil have?
A) 12 nickels and 108 dimes
B) 13 nickels and 117 dimes
C) 11 nickels and 99 dimes
D) 108 nickels and 12 dimes
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is more than the value of the nickels. How many nickels and dimes does Jamil have?
A) 12 nickels and 108 dimes
B) 13 nickels and 117 dimes
C) 11 nickels and 99 dimes
D) 108 nickels and 12 dimes

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
73
Solve Problems Using Systems of Linear Equations
A rectangular lot whose perimeter is 400 feet is fenced along three sides. An expensive fencing along the lot's length costs per foot, and an inexpensive fencing along the two side widths costs only per foot. The total cost of the fencing along the three sides comes to . What are the lot's dimensions?
A) Length ; Width
B) Length ; Width
C) Length ; Width
D) Length ; Width
A rectangular lot whose perimeter is 400 feet is fenced along three sides. An expensive fencing along the lot's length costs per foot, and an inexpensive fencing along the two side widths costs only per foot. The total cost of the fencing along the three sides comes to . What are the lot's dimensions?
A) Length ; Width
B) Length ; Width
C) Length ; Width
D) Length ; Width

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
74
Solve Problems Using Systems of Linear Equations
In 1985, in the town of Appleby, of Hispanics were overweight, increasing by an average of per year. In 1985, in the town of Appleby, of whites were overweight, increasing by an average of per year. If these trends continue, in which year will the percentage of Hispanics who are overweight be the same as the percentage of whites who are overweight? Round to the nearest year. What percentage of Hispanics (to the nearest whole percent) will be overweight at that time?
A)
B)
C)
D)
In 1985, in the town of Appleby, of Hispanics were overweight, increasing by an average of per year. In 1985, in the town of Appleby, of whites were overweight, increasing by an average of per year. If these trends continue, in which year will the percentage of Hispanics who are overweight be the same as the percentage of whites who are overweight? Round to the nearest year. What percentage of Hispanics (to the nearest whole percent) will be overweight at that time?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
75
Solve Problems Using Systems of Linear Equations
In 1985, in the town of Appleby, of Hispanics were overweight, increasing by an average of per year. In 1985, in the town of Appleby, of whites were overweight, increasing by an average of per year. Write a function that models the percentage, , of Hispanics who are overweight x years after 1985. Write a function that models the percentage, , of whites who are overweight x years after
A) Hispanics:
Whites:
B) Hispanics:
Whites:
C) Hispanics:
Whites:
D) Hispanics:
Whites:
In 1985, in the town of Appleby, of Hispanics were overweight, increasing by an average of per year. In 1985, in the town of Appleby, of whites were overweight, increasing by an average of per year. Write a function that models the percentage, , of Hispanics who are overweight x years after 1985. Write a function that models the percentage, , of whites who are overweight x years after
A) Hispanics:
Whites:
B) Hispanics:
Whites:
C) Hispanics:
Whites:
D) Hispanics:
Whites:

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
76
Solve Problems Using Systems of Linear Equations
A twin-engined aircraft can fly 1330 miles from city A to city B in 5 hours with the wind and make the return trip in 7 hours against the wind. What is the speed of the wind?
A)
B)
C)
D)
A twin-engined aircraft can fly 1330 miles from city A to city B in 5 hours with the wind and make the return trip in 7 hours against the wind. What is the speed of the wind?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
77
Solve Problems Using Systems of Linear Equations
As the price of a product increases, the demand for that product decreases. However, at higher prices, suppliers are willing to produce greater quantities of the product. The weekly supply and demand models for a certain type of television are as follows:
Demand:
Supply:
where is the price in dollars per television.
Find the price at which supply and demand are equal. At this price, how many televisions can be supplied and sold each week?
A)
B)
C)
D)
As the price of a product increases, the demand for that product decreases. However, at higher prices, suppliers are willing to produce greater quantities of the product. The weekly supply and demand models for a certain type of television are as follows:
Demand:
Supply:
where is the price in dollars per television.
Find the price at which supply and demand are equal. At this price, how many televisions can be supplied and sold each week?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
78
Solve Problems Using Systems of Linear Equations
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 11 feet more than 5 times the width. He needs 70 feet of fencing to do the job. Find the length and width of the garden.
A) length: 31 feet; width: 4 feet
B) length: feet; width: feet
C) length: 36 feet; width: 5 feet
D) length: 26 feet; width: 3 feet
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 11 feet more than 5 times the width. He needs 70 feet of fencing to do the job. Find the length and width of the garden.
A) length: 31 feet; width: 4 feet
B) length: feet; width: feet
C) length: 36 feet; width: 5 feet
D) length: 26 feet; width: 3 feet

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
79
Solve Problems Using Systems of Linear Equations
The Family Fine Arts Center charges per adult and per senior citizen for its performances. On a recent weekend evening when 502 people paid admission, the total receipts were . How many who paid were senior citizens?
A) 322 senior citizens
B) 180 senior citizens
C) 232 senior citizens
D) 270 senior citizens
The Family Fine Arts Center charges per adult and per senior citizen for its performances. On a recent weekend evening when 502 people paid admission, the total receipts were . How many who paid were senior citizens?
A) 322 senior citizens
B) 180 senior citizens
C) 232 senior citizens
D) 270 senior citizens

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck
80
Solve Problems Using Systems of Linear Equations
In Miguel's home town, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing. The function models the percentage, , of women in this city who smoke x years after 1990 . The function models the percentage, , of men in this city who smoke x years after 1990 . Use these models to determine when the percentage of women who smoke will be the same as the percentage of men who smoke. Round to the nearest year. What percentage of women and what percentage of men (to the nearest whole percent) will smoke at that time?
A)
B)
C)
D)
In Miguel's home town, the percentage of women who smoke is increasing while the percentage of men who smoke is decreasing. The function models the percentage, , of women in this city who smoke x years after 1990 . The function models the percentage, , of men in this city who smoke x years after 1990 . Use these models to determine when the percentage of women who smoke will be the same as the percentage of men who smoke. Round to the nearest year. What percentage of women and what percentage of men (to the nearest whole percent) will smoke at that time?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 288 flashcards in this deck.
Unlock Deck
k this deck


