Deck 7: Additional Topics in Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/264
Play
Full screen (f)
Deck 7: Additional Topics in Trigonometry
1
Solve the triangle.
A)
B)
C)
D)
A)
B)
C)
D)
A
2
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) ;
B) ;
C)
D) no triangle
A) ;
B) ;
C)
D) no triangle
A
3
Solve Applied Problems Using the Law of Sines
Two tracking stations are on the equator 130 miles apart. A weather balloon is located on a bearing of from the western station and on a bearing of N22 from the eastern station. How far is the balloon from the western station? Round to the nearest mile.
A) 134 miles
B) 143 miles
C) 107 miles
D) 98 miles
Two tracking stations are on the equator 130 miles apart. A weather balloon is located on a bearing of from the western station and on a bearing of N22 from the eastern station. How far is the balloon from the western station? Round to the nearest mile.
A) 134 miles
B) 143 miles
C) 107 miles
D) 98 miles
A
4
Solve the triangle.
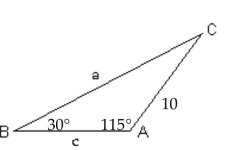
A)
B)
C)
D) Solve the triangle. Round lengths to the nearest tenth and angle measures to the nearest degree.

A)
B)
C)
D) Solve the triangle. Round lengths to the nearest tenth and angle measures to the nearest degree.

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
5
Find the Area of an Oblique Triangle Using the Sine Function
yards, yards
A) 2 square yards
B) 5 square yards
C) 10 square yards
D) 1 square yards
yards, yards
A) 2 square yards
B) 5 square yards
C) 10 square yards
D) 1 square yards

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
6
Solve Applied Problems Using the Law of Sines
A surveyor standing 50 meters from the base of a building measures the angle to the top of the building and finds it to be . The surveyor then measures the angle to the top of the radio tower on the building and finds that it is . How tall is the radio tower?
A) meters
B) meters
C) meters
D) meters
A surveyor standing 50 meters from the base of a building measures the angle to the top of the building and finds it to be . The surveyor then measures the angle to the top of the radio tower on the building and finds that it is . How tall is the radio tower?
A) meters
B) meters
C) meters
D) meters

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
7
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) no triangle
B)
C)
D)
A) no triangle
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
8
Find the Area of an Oblique Triangle Using the Sine Function
feet, feet
A) 4 square feet
B) 9 square feet
C) 18 square feet
D) 10 square feet
feet, feet
A) 4 square feet
B) 9 square feet
C) 18 square feet
D) 10 square feet

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
9
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) no triangle
B)
C)
D)
A) no triangle
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
10
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) ;
B)
C)
D) no triangle
A) ;
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
11
Solve Applied Problems Using the Law of Sines
To find the distance across a river, a distance of is laid off on one side of the river. It is found that and . Find . Round to the nearest meter.
A) 115 meters
B) 118 meters
C) 90 meters
D) 87 meters
To find the distance across a river, a distance of is laid off on one side of the river. It is found that and . Find . Round to the nearest meter.
A) 115 meters
B) 118 meters
C) 90 meters
D) 87 meters

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
12
Find the Area of an Oblique Triangle Using the Sine Function
meters, meters
A) 19 square meters
B) 10 square meters
C) 38 square meters
D) 40 square meters
meters, meters
A) 19 square meters
B) 10 square meters
C) 38 square meters
D) 40 square meters

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
13
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) no triangle
B)
C)
D)
A) no triangle
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
14
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A) ;
B) ;
C)
D) no triangle
A) ;
B) ;
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the triangle.
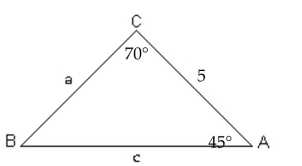
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the triangle.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
17
Use the Law of Sines to Solve, if Possible, the Triangle or Triangles in the Ambiguous Case
A)
B)
C)
D) no triangle
A)
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the triangle.
A) B
B)
C)
D)
A) B
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the triangle.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
20
Find the Area of an Oblique Triangle Using the Sine Function
inches, inches
A) 16 square inches
B) 31 square inches
C) 14 square inches
D) 33 square inches
inches, inches
A) 16 square inches
B) 31 square inches
C) 14 square inches
D) 33 square inches

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
21
Solve Applied Problems Using the Law of Cosines
A painter needs to cover a triangular region 61 meters by 68 meters by 72 meters. A can of paint covers 70 square meters. How many cans will be needed?
A) 28 cans
B) 314 cans
C) 14 cans
D) 3 cans
A painter needs to cover a triangular region 61 meters by 68 meters by 72 meters. A can of paint covers 70 square meters. How many cans will be needed?
A) 28 cans
B) 314 cans
C) 14 cans
D) 3 cans

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
22
Solve Applied Problems Using the Law of Cosines
Two sailboats leave a harbor in the Bahamas at the same time. The first sails at in a direction . The second sails at in a direction . Assuming that both boats maintain speed and heading, after 4 hours, how far apart are the boats?
A) miles
B) miles
C) miles
D) miles
Two sailboats leave a harbor in the Bahamas at the same time. The first sails at in a direction . The second sails at in a direction . Assuming that both boats maintain speed and heading, after 4 hours, how far apart are the boats?
A) miles
B) miles
C) miles
D) miles

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
23
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
24
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
25
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
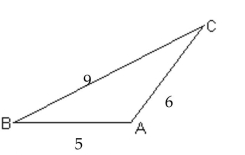
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
26
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
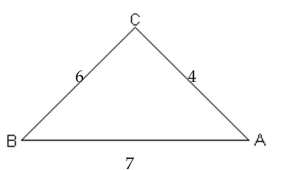
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
27
Solve Applied Problems Using the Law of Cosines
Two airplanes leave an airport at the same time, one going northwest (bearing ) at and the other going east at . How far apart are the planes after 2 hours (to the nearest mile)?
A) 1422 miles
B) 711 miles
C) 1184 miles
D) 1268 miles
Two airplanes leave an airport at the same time, one going northwest (bearing ) at and the other going east at . How far apart are the planes after 2 hours (to the nearest mile)?
A) 1422 miles
B) 711 miles
C) 1184 miles
D) 1268 miles

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
28
Solve Applied Problems Using the Law of Cosines
The distance from home plate to dead center field in Sun Devil Stadium is 406 feet. A baseball diamond is a square with a distance from home plate to first base of 90 feet. How far is it from first base to dead center field?
A) feet
B) feet
C) feet
D) feet
The distance from home plate to dead center field in Sun Devil Stadium is 406 feet. A baseball diamond is a square with a distance from home plate to first base of 90 feet. How far is it from first base to dead center field?
A) feet
B) feet
C) feet
D) feet

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
29
Additional Concepts
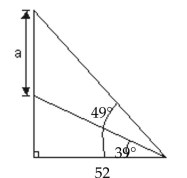
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
30
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
31
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
32
Solve Applied Problems Using the Law of Cosines
A plane flying a straight course observes a mountain at a bearing of to the right of its course. At that time the plane is 8 kilometers from the mountain. A short time later, the bearing to the mountain becomes . How far is the plane from the mountain when the second bearing is taken (to the nearest tenth of a
A) kilometers
B) kilometers
C) kilometers
D) kilometers
A plane flying a straight course observes a mountain at a bearing of to the right of its course. At that time the plane is 8 kilometers from the mountain. A short time later, the bearing to the mountain becomes . How far is the plane from the mountain when the second bearing is taken (to the nearest tenth of a
A) kilometers
B) kilometers
C) kilometers
D) kilometers

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
33
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D) no triangle

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
34
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
35
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
36
Additional Concepts
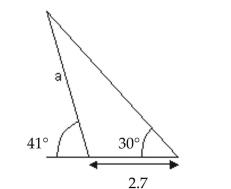
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
37
Solve Applied Problems Using the Law of Cosines
Two points and are on opposite sides of a building. A surveyor selects a third point to place a transit. Point is 54 feet from point and 72 feet from point . The angle is . How far apart are points and ?
A) feet
B) feet
C) feet
D) feet
Two points and are on opposite sides of a building. A surveyor selects a third point to place a transit. Point is 54 feet from point and 72 feet from point . The angle is . How far apart are points and ?
A) feet
B) feet
C) feet
D) feet

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
38
Solve Applied Problems Using the Law of Sines
A guy wire to a tower makes a angle with level ground. At a point farther from the tower than the wire but on the same side as the base of the wire, the angle of elevation to the top of the tower is . Find the length of the wire (to the nearest foot).
A) 31 feet
B) 36 feet
C) 62 feet
D) 67 feet
A guy wire to a tower makes a angle with level ground. At a point farther from the tower than the wire but on the same side as the base of the wire, the angle of elevation to the top of the tower is . Find the length of the wire (to the nearest foot).
A) 31 feet
B) 36 feet
C) 62 feet
D) 67 feet

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
39
The Law of Cosines
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)
1 Use the Law of Cosines to Solve Oblique Triangles
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
40
Use Heron's Formula to Find the Area of a Triangle
yards, yards, yards
A) 110 square yards
B) 113 square yards
C) 116 square yards
D) 119 square yards
yards, yards, yards
A) 110 square yards
B) 113 square yards
C) 116 square yards
D) 119 square yards

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
41
Convert a Point from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
42
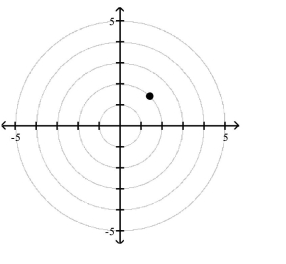
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
A)
B)
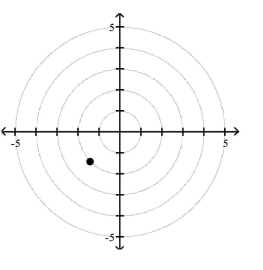 C)
C)
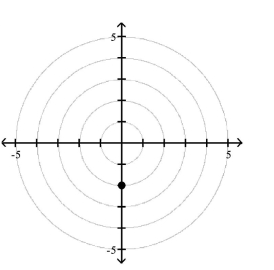
D)
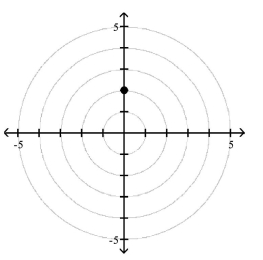
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)
 C)
C)
D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
43
Convert a Point from Polar to Rectangular Coordinates
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
44
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
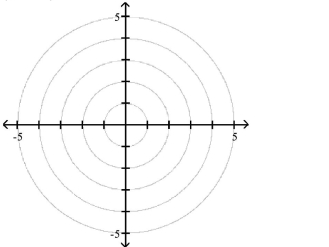
A)
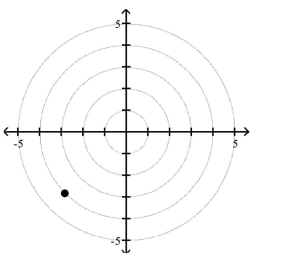
B)
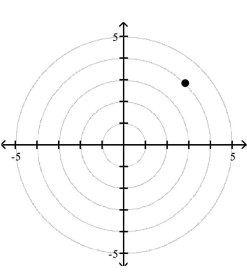
C)
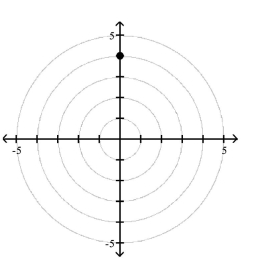
D)
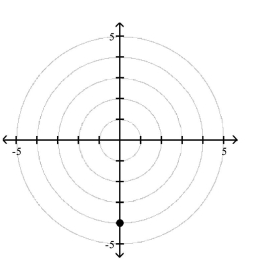
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
48
Convert a Point from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
and
A)
B)
C)
D) Select the representation that does not change the location of the given point.
and
A)
B)
C)
D) Select the representation that does not change the location of the given point.

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
50
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
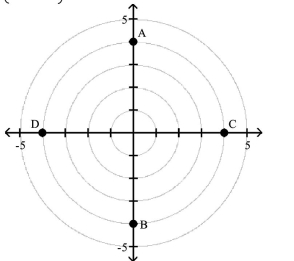
A)
B)
C) B
D) Use a polar coordinate system to plot the point with the given polar coordinates.
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)
B)
C) B
D) Use a polar coordinate system to plot the point with the given polar coordinates.

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
52
Convert a Point from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
53
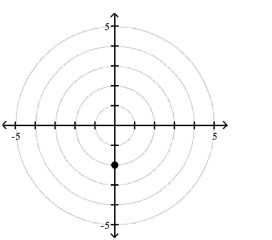
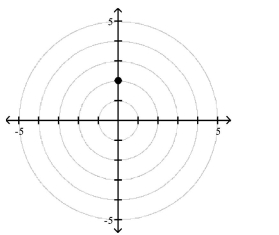
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
A)
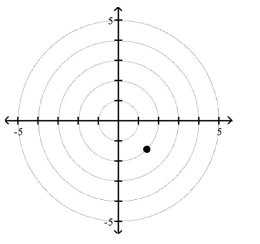
B)
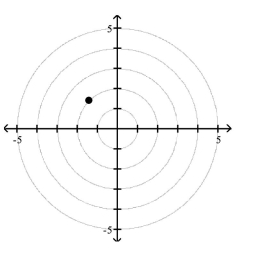 C)
C)
D)
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)
 C)
C)
D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
54
Use Heron's Formula to Find the Area of a Triangle
inches, inches, inches
A) 14 square inches
B) 27 square inches
C) 12 square inches
D) 29 square inches
inches, inches, inches
A) 14 square inches
B) 27 square inches
C) 12 square inches
D) 29 square inches

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
55
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
A)
B)
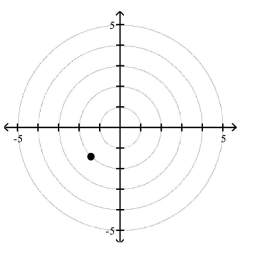
C)
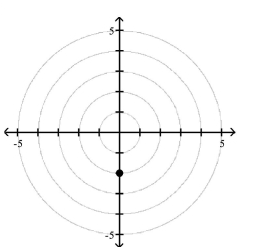
D)
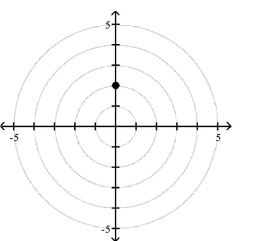
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
56
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
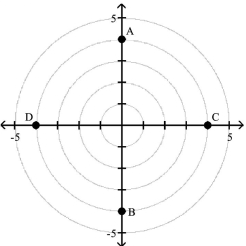
A)
B)
C)
D)
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
57
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
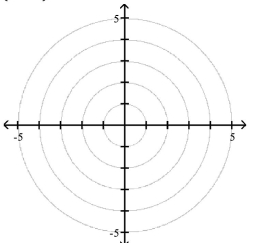
A)
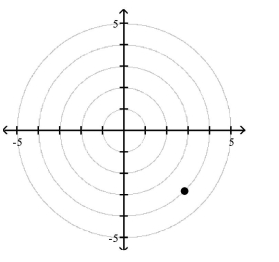
B)
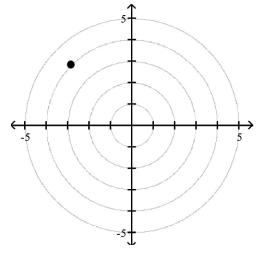
C)
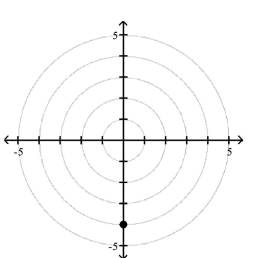
D)
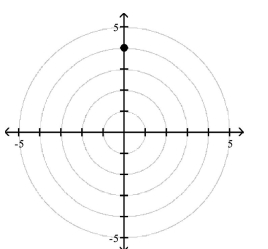
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
58
Polar Coordinates
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.
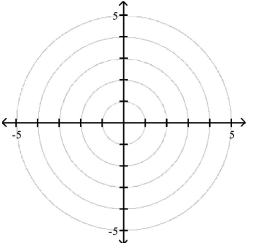
A)
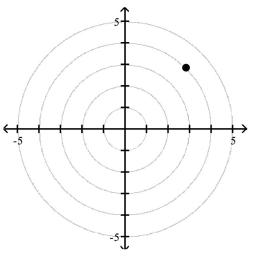
B)
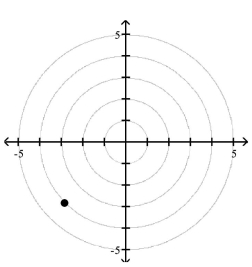
C)
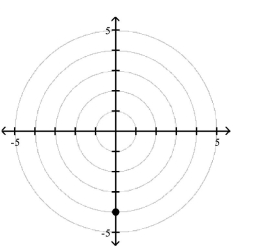
D)
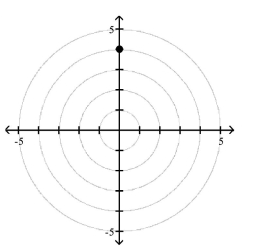
1 Plot Points in the Polar Coordinate System
Match the point in polar coordinates with either A, B, C, or D on the graph.

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
59
Use Heron's Formula to Find the Area of a Triangle
meters, meters, meters
A) 28 square meters
B) 14 square meters
C) 56 square meters
D) 58 square meters
meters, meters, meters
A) 28 square meters
B) 14 square meters
C) 56 square meters
D) 58 square meters

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
and
A)
B)
C)
D)
and
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
61
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
62
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
63
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
64
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
65
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
66
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
67
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
68
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
69
Convert an Equation from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
70
Convert an Equation from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
71
Convert a Point from Polar to Rectangular Coordinates
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
72
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
73
Convert a Point from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
74
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
75
Convert a Point from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
76
Convert a Point from Polar to Rectangular Coordinates
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
77
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
78
Convert an Equation from Polar to Rectangular Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
79
Convert an Equation from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck
80
Convert a Point from Rectangular to Polar Coordinates
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 264 flashcards in this deck.
Unlock Deck
k this deck


