Deck 5: Number Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/171
Play
Full screen (f)
Deck 5: Number Theory
1
Every composite number is divisible by 2.
False
2
Use divisibility tests to decide whether the first number is divisible by the second.
615,849; 9
A)Yes
B)No
615,849; 9
A)Yes
B)No
B
3
Find all natural number factors of the number.
484
A)1, 2, 3, 4, 11, 22, 121, 242, 484
B)1, 2, 4, 11, 22, 44, 121, 242, 484
C)1, 2, 11, 121, 484
D)1, 2, 4, 11, 22, 33, 44, 121, 242, 484
484
A)1, 2, 3, 4, 11, 22, 121, 242, 484
B)1, 2, 4, 11, 22, 44, 121, 242, 484
C)1, 2, 11, 121, 484
D)1, 2, 4, 11, 22, 33, 44, 121, 242, 484
B
4
All prime numbers are odd.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
5
Find all natural number factors of the number.
47
A)1, 47
B)1, 2, 3, 15, 23, 47
C)1, 2, 4, 15, 23, 47
D)1, 2, 23, 47
47
A)1, 47
B)1, 2, 3, 15, 23, 47
C)1, 2, 4, 15, 23, 47
D)1, 2, 23, 47

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
6
Use divisibility tests to decide whether the first number is divisible by the second.
938,772; 9
A)Yes
B)No
938,772; 9
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
7
Find all natural number factors of the number.
110
A)2, 5, 10, 11, 55, 110
B)1, 2, 5, 10, 11, 22, 110
C)1, 2, 5, 10, 11, 22, 55, 110
D)1, 2, 4, 5, 10, 11, 22, 55, 110
110
A)2, 5, 10, 11, 55, 110
B)1, 2, 5, 10, 11, 22, 110
C)1, 2, 5, 10, 11, 22, 55, 110
D)1, 2, 4, 5, 10, 11, 22, 55, 110

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
8
If a number is divisible by both 3 and 9 then it is divisible by 27.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
9
If n is a natural number and 20|n, then 10|n.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
10
If a natural number is divisible by 2, then it must also be divisible by 10.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
11
Use divisibility tests to decide whether the first number is divisible by the second.
574,085; 4
A)Yes
B)No
574,085; 4
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
12
Find all natural number factors of the number.
42
A)1, 2, 3, 7, 6, 14, 21, 42
B)1, 2, 3, 7, 6, 14, 28, 42
C)1, 7, 42
D)7, 6, 14, 42
42
A)1, 2, 3, 7, 6, 14, 21, 42
B)1, 2, 3, 7, 6, 14, 28, 42
C)1, 7, 42
D)7, 6, 14, 42

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
13
If a natural number is divisible by 3 and 5, then it must also be divisible by 15.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
14
Use divisibility tests to decide whether the first number is divisible by the second.
6,955,200; 7 [Note that a divisibility test for 7 is as follows:
Double the last digit of the number and subtract this value from the original number with the last
Digit omitted. Repeat this process as many times as necessary until the number obtained can easily
Be divided by 7. If the final number obtained is divisible by 7, then so is the original number. If the
Final number obtained is not divisible by 7, then neither is the original number.]
A)Yes
B)No
6,955,200; 7 [Note that a divisibility test for 7 is as follows:
Double the last digit of the number and subtract this value from the original number with the last
Digit omitted. Repeat this process as many times as necessary until the number obtained can easily
Be divided by 7. If the final number obtained is divisible by 7, then so is the original number. If the
Final number obtained is not divisible by 7, then neither is the original number.]
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
15
Use divisibility tests to decide whether the first number is divisible by the second.
467,661; 3
A)Yes
B)No
467,661; 3
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
16


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
17
There are 35 prime numbers smaller than 150.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
18
A prime number may have one or two different natural number factors but may not have more
than two different natural number factors.
than two different natural number factors.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
19
Find all natural number factors of the number.
125
A)1, 5, 25
B)1, 5, 25, 125
C)5, 62, 125
D)5, 25, 125
125
A)1, 5, 25
B)1, 5, 25, 125
C)5, 62, 125
D)5, 25, 125

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
20
Use divisibility tests to decide whether the first number is divisible by the second.
404,036; 4
A)Yes
B)No
404,036; 4
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
21
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
533x is divisible by 11.
533x is divisible by 11.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
22
Give the prime factorization of the number. Use exponents when possible.
4725
4725


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
23
Give the prime factorization of the number. Use exponents when possible.
177
177


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
24
Give the prime factorization of the number. Use exponents when possible.
396
396


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
25
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
74,3x2 is divisible by 6.
74,3x2 is divisible by 6.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
26
Give the prime factorization of the number. Use exponents when possible.
154
154


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
27
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
214,21x is divisible by 11.
214,21x is divisible by 11.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
28
Use divisibility tests to decide whether the first number is divisible by the second.
322,695; 9
A)Yes
B)No
322,695; 9
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
29
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
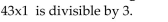
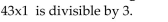

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
30
Use divisibility tests to decide whether the first number is divisible by the second.
827,711; 5
A)Yes
B)No
827,711; 5
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
31
Use divisibility tests to decide whether the first number is divisible by the second.
139,243,105; 11 [Note that a divisibility test for 11 is as follows:
Starting at the left of the number, add together every other digit. Add together the remaining digits.
Subtract the smaller of the two sums from the larger. If the final number obtained is divisible by 11,
Then so is the original number. If the final number obtained is not divisible by 11, then neither is the
Original number.]
A)Yes
B)No
139,243,105; 11 [Note that a divisibility test for 11 is as follows:
Starting at the left of the number, add together every other digit. Add together the remaining digits.
Subtract the smaller of the two sums from the larger. If the final number obtained is divisible by 11,
Then so is the original number. If the final number obtained is not divisible by 11, then neither is the
Original number.]
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
32
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
43x2 is divisible by 9.
43x2 is divisible by 9.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
33
Give the prime factorization of the number. Use exponents when possible.
2937
2937


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
34
414,3x2 is divisible by 8 but not 16.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
35
Use divisibility tests to decide whether the first number is divisible by the second.
348,951; 10
A)Yes
B)No
348,951; 10
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
36
Give the prime factorization of the number. Use exponents when possible.
28
28


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
37
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
4x21 is divisible by 4.
4x21 is divisible by 4.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
38
Give the prime factorization of the number. Use exponents when possible.
936
936


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
39
Give the prime factorization of the number. Use exponents when possible.
198
198


Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
40
Determine all values for the digit x that make the first number divisible by the second number. If none exist, so state.
43x6 is divisible by 4.
43x6 is divisible by 4.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
41
Every natural number of the form 4k + 5 is prime.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
42
Find the number of divisors of the number.
360
A)36
B)12
C)24
D)18
360
A)36
B)12
C)24
D)18

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
43
Use the formula indicated to determine the prime number generated for the given value of n.
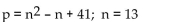
A)223
B)2797
C)141
D)197
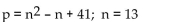
A)223
B)2797
C)141
D)197

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
44
43x0 is divisible by 6.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
45
Use the formula indicated to determine the prime number generated for the given value of n.
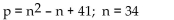
A)1163
B)3801
C)2241
D)1149
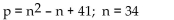
A)1163
B)3801
C)2241
D)1149

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
46
Use the formula indicated to determine the prime number generated for the given value of n.
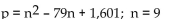
A)2393
B)113
C)-809
D)971
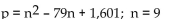
A)2393
B)113
C)-809
D)971

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
47
Find the number of divisors of the number.



Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
48
Determine whether the statement is true or false.
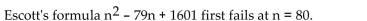
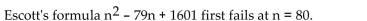

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
49
Use the formula indicated to determine the prime number generated for the given value of n.
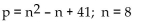
A)97
B)2297
C)15
D)113
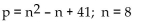
A)97
B)2297
C)15
D)113

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
50
Determine whether the statement is true or false.
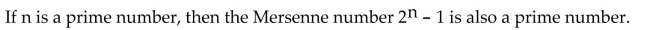
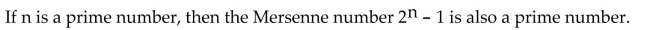

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
51
417,30x is divisible by 8 but not 16.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
52
Determine whether the statement is true or false.
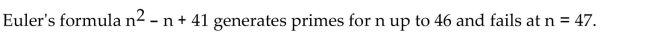
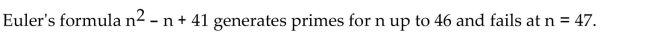

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
53
Use the formula indicated to determine the prime number generated for the given value of n.
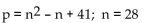
A)1395
B)771
C)797
D)853
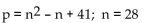
A)1395
B)771
C)797
D)853

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
54
Find the number of divisors of the number.
400
A)16
B)8
C)12
D)15
400
A)16
B)8
C)12
D)15

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
55
Find the number of divisors of the number.
54
A)12
B)6
C)9
D)8
54
A)12
B)6
C)9
D)8

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
56
Use the formula indicated to determine the prime number generated for the given value of n.
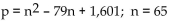
A)7759
B)4201
C)10,961
D)691
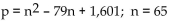
A)7759
B)4201
C)10,961
D)691

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
57
Determine whether the statement is true or false.
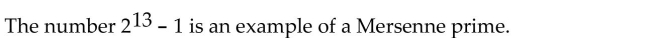
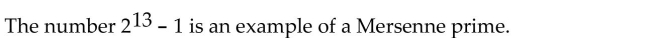

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
58
Determine whether the statement is true or false.
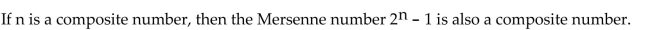
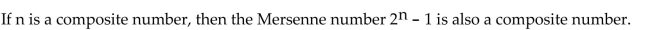

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
59
Find the number of divisors of the number.
60
A)14
B)12
C)16
D)10
60
A)14
B)12
C)16
D)10

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
60
Every natural number of the form 4k + 4 is prime.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
61
All prime numbers are also deficient numbers.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
62
Determine whether the number is abundant or deficient.
108
A)Abundant
B)Deficient
108
A)Abundant
B)Deficient

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
63
Determine whether the statement is true or false.
The proper divisors of a natural number include all divisors of the number except 1.
The proper divisors of a natural number include all divisors of the number except 1.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
64
All composite numbers are also abundant numbers.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
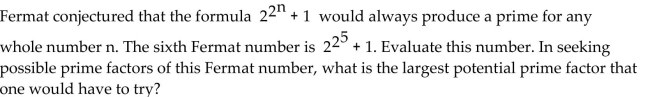
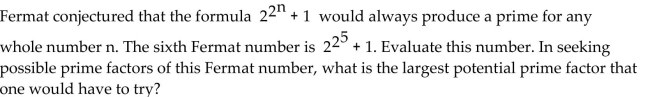

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
66
Use the formula indicated to determine the prime number generated for the given value of n.
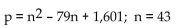
A)53
B)1847
C)3645
D)6847
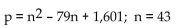
A)53
B)1847
C)3645
D)6847

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
67
520 and 616 are amicable numbers.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
68
Determine whether the number is abundant or deficient.
8
A)Abundant
B)Deficient
8
A)Abundant
B)Deficient

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
69
Determine whether the number is abundant or deficient.
18
A)Abundant
B)Deficient
18
A)Abundant
B)Deficient

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
70
Twin primes are prime numbers whose difference is a multiple of 4.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
71
Determine whether the statement is true or false.
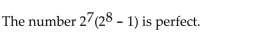
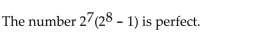

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.



Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
73
Determine whether the statement is true or false.
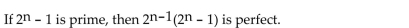
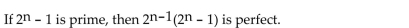

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
74
A natural number which is not deficient must be abundant.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the problem.



Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
76
Not all perfect numbers end in 6 or 28.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem.
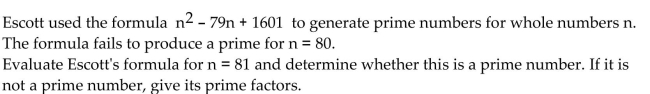
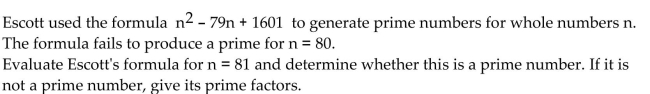

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
78
There is no largest prime number.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
79
Determine whether the number is abundant or deficient.
30
A)Abundant
B)Deficient
30
A)Abundant
B)Deficient

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
80
Determine whether the number is abundant or deficient.
95
A)Deficient
B)Abundant
95
A)Deficient
B)Abundant

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck


