Deck 16: Voting and Apportionment
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/99
Play
Full screen (f)
Deck 16: Voting and Apportionment
1
Solve the problem.
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table. Use the Borda Method to determine the winner.
Use the Borda Method to determine the winner.
A)Denise
B)Brett
C)Carol
D)Andy
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table.
 Use the Borda Method to determine the winner.
Use the Borda Method to determine the winner.A)Denise
B)Brett
C)Carol
D)Andy
D
2
Solve the problem.
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S). Determine the winner using the pairwise comparison method and state whether the winner
Determine the winner using the pairwise comparison method and state whether the winner
Received a majority of votes.
A)Jones; no
B)Jones; yes
C)Smith; yes
D)Smith; no
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
 Determine the winner using the pairwise comparison method and state whether the winner
Determine the winner using the pairwise comparison method and state whether the winnerReceived a majority of votes.
A)Jones; no
B)Jones; yes
C)Smith; yes
D)Smith; no
D
3
Solve the problem.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile. Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received a
Majority of votes.
A)Hawaii; no
B)Florida; no
C)Alaska; no
D)San Antonio; no
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile.
 Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received aMajority of votes.
A)Hawaii; no
B)Florida; no
C)Alaska; no
D)San Antonio; no
B
4
Eight voters are asked to rank 3 brands of automobiles: A, B, and C. The eight voters turn in the following ballots showing their preferences in order: 


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the problem.
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S). Determine the winner using the Hare method and state whether the winner received a majority of
Determine the winner using the Hare method and state whether the winner received a majority of
Votes.
A)Smith, yes
B)Jones; no
C)Smith; no
D)Jones; yes
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
 Determine the winner using the Hare method and state whether the winner received a majority of
Determine the winner using the Hare method and state whether the winner received a majority ofVotes.
A)Smith, yes
B)Jones; no
C)Smith; no
D)Jones; yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the problem.
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table. Use the Hare Method to determine the winner.
Use the Hare Method to determine the winner.
A)Carol
B)Andy
C)Denise
D)Brett
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table.
 Use the Hare Method to determine the winner.
Use the Hare Method to determine the winner.A)Carol
B)Andy
C)Denise
D)Brett

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem.
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table. Use the Plurality Method to determine the winner.
Use the Plurality Method to determine the winner.
A)Andy
B)Carol
C)Brett
D)Denise
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table.
 Use the Plurality Method to determine the winner.
Use the Plurality Method to determine the winner.A)Andy
B)Carol
C)Brett
D)Denise

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
8


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the problem.
A condominium association is holding an election for president of the board of directors. Each member ranks the candidates from first to third. The voter profile below shows the results of the
Ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).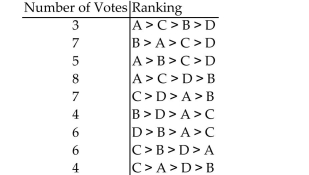 Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received a
Majority of votes.
A)Downs; no
B)Abbott; no
C)Blake; no
D)Cleary; no
A condominium association is holding an election for president of the board of directors. Each member ranks the candidates from first to third. The voter profile below shows the results of the
Ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).
 Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received aMajority of votes.
A)Downs; no
B)Abbott; no
C)Blake; no
D)Cleary; no

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
10
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile.
The following voter profile.


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
11
Eight voters are asked to rank 4 brands of ice cream: A, B, C, and D. The eight voters turn in the following ballots showing their preferences in order: 


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the problem.
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table. Use the Pairwise Comparison Method to determine the winner.
Use the Pairwise Comparison Method to determine the winner.
A)Denise
B)Andy
C)Brett
D)Carol
Four members are running for president of the Greater New Orleans Stamp Club: Andy (a), Brett (b), Carol (c), and Denise (d). The voter profile is summarized in the table.
 Use the Pairwise Comparison Method to determine the winner.
Use the Pairwise Comparison Method to determine the winner.A)Denise
B)Andy
C)Brett
D)Carol

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
13


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the problem.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile.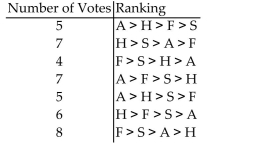 Determine the winner using the Hare method and state whether the winner received a majority of
Determine the winner using the Hare method and state whether the winner received a majority of
Votes.
A)Hawaii; yes
B)Alaska; yes
C)Alaska; no
D)Hawaii; no
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile.
 Determine the winner using the Hare method and state whether the winner received a majority of
Determine the winner using the Hare method and state whether the winner received a majority ofVotes.
A)Hawaii; yes
B)Alaska; yes
C)Alaska; no
D)Hawaii; no

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the problem.
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).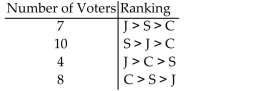 Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received a
Majority of votes.
A)Smith; yes
B)Jones; no
C)Smith; no
D)Jones; yes
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
 Determine the winner using the Borda count method and state whether the winner received a
Determine the winner using the Borda count method and state whether the winner received aMajority of votes.
A)Smith; yes
B)Jones; no
C)Smith; no
D)Jones; yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
16
Ten voters are asked to rank 4 brands of cell phones: A, B, C, and D. The ten voters turn in the following ballots showing their preferences in order: 


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the problem.
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S). Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majority
Of votes.
A)Clark; yes
B)Jones; no
C)Smith; yes
D)Clark; no
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the ballots with
Candidates Clark (C), Jones (J), and Smith (S).
 Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majorityOf votes.
A)Clark; yes
B)Jones; no
C)Smith; yes
D)Clark; no

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the problem.
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile. Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majority
Of votes.
A)Hawaii; no
B)Alaska; no
C)Hawaii; yes
D)Alaska; yes
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile.
 Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majorityOf votes.
A)Hawaii; no
B)Alaska; no
C)Hawaii; yes
D)Alaska; yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
19
Ten voters are asked to rank 3 brands of shoes: A, B, and C. The ten voters turn in the following ballots showing their preferences in order: 


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the problem.
A condominium association is holding an election for president of the board of directors. Each member ranks the candidates from first to third. The voter profile below shows the results of the
Ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D). Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majority
Of votes.
A)Abbott; no
B)Cleary; no
C)Abbott; yes
D)Cleary; yes
A condominium association is holding an election for president of the board of directors. Each member ranks the candidates from first to third. The voter profile below shows the results of the
Ballots with candidates Abbott(A), Blake (B), Cleary (C), and Downs (D).
 Determine the winner using the plurality method and state whether the winner received a majority
Determine the winner using the plurality method and state whether the winner received a majorityOf votes.
A)Abbott; no
B)Cleary; no
C)Abbott; yes
D)Cleary; yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
21

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
22
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Borda Method. Does the Borda Method violate the Condorcet
Criterion for the voter profile?
Criterion for the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
23
Given the following voter profile, determine who has the majority of first place votes and then use the Borda Method to determine the outcome. Does the Borda method violate the majority criterion
For the voter profile?
For the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
24
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Plurality Method. Does the Plurality Method violate the Condorcet
Criterion for the voter profile?
Criterion for the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
25
For the voter profile given below, who (or what)is selected if a second runoff election is held between the two candidates with the most first place votes? 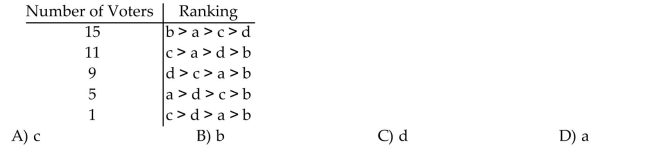
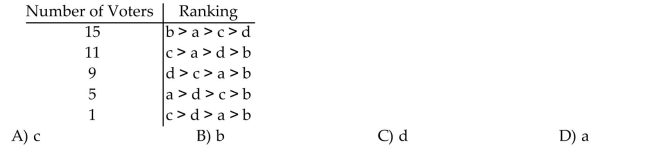

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
26
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Borda Method. Does the Borda Method violate the Condorcet
Criterion for the voter profile?
Criterion for the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose 8 candidates a, b, c, d, e, f, g, h are involved in a Pairwise Comparison Method election. The number of pairwise comparisons each candidate wins is shown in the table. 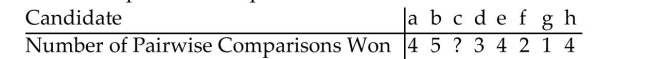 How many comparisons does candidate c win?
How many comparisons does candidate c win?
A)5
B)4
C)3
D)6
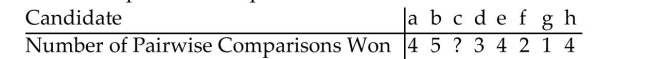 How many comparisons does candidate c win?
How many comparisons does candidate c win?A)5
B)4
C)3
D)6

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
28
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Plurality Method. Does the Plurality Method violate the Condorcet
Criterion for the voter profile?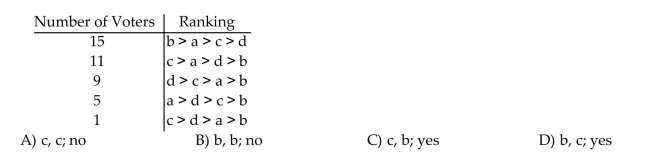
Criterion for the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
29
Given the following voter profile, determine who has the majority of first place votes and then use the Borda Method to determine the outcome. Does the Borda method violate the majority criterion
For the voter profile?
For the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
30
For the voter profile given below, who (or what)is selected if a runoff election is held between the candidates that rank second and third; and the winner of that election faces the candidate with the
Most first place votes, to decide the final outcome of the election?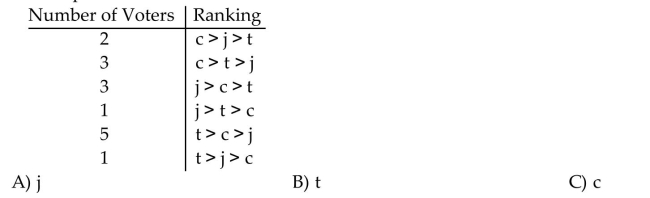
Most first place votes, to decide the final outcome of the election?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
31
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Hare Method. Does the Hare Method violate the Condorcet criterion
For the voter profile?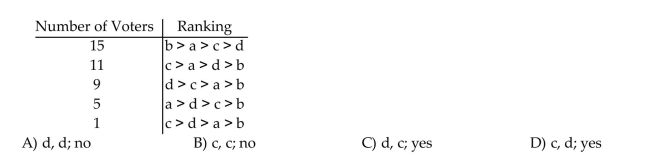
For the voter profile?

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
32
How many different pairwise comparisons are needed to learn the outcome of an election involving n = 5 candidates?
A)30
B)40
C)10
D)20
A)30
B)40
C)10
D)20

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
33
Suppose 8 candidates a, b, c, d, e, f, g, h are involved in a Pairwise Comparison Method election. The number of pairwise comparisons each candidate wins is shown in the table. 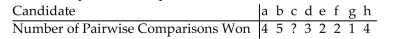 Which candidate wins the election and how many pairwise points does the winner have?
Which candidate wins the election and how many pairwise points does the winner have?
A)c, with 7 pairwise points
B)c, with 5 pairwise points
C)c, with 8 pairwise points
D)c, with 6 pairwise points
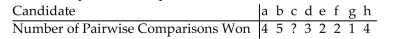 Which candidate wins the election and how many pairwise points does the winner have?
Which candidate wins the election and how many pairwise points does the winner have?A)c, with 7 pairwise points
B)c, with 5 pairwise points
C)c, with 8 pairwise points
D)c, with 6 pairwise points

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
34
Given the following voter profile, determine who has the majority of first place votes and then use the Borda Method to determine the outcome. Does the Borda method violate the majority criterion
For the voter profile?
For the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
35


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
36
Twenty-five voters are using the Borda method to select one of five candidates: a, b, c, d, or e. If Candidate a receives 32 Borda points, Candidate b receives 58 Borda points, Candidate c receives 46
Borda points, and Candidate d receives 55 Borda points, how many Borda points does Candidate e
Receive? Who wins the Borda election?
A)48; b
B)55; b
C)184; e
D)59; e
Borda points, and Candidate d receives 55 Borda points, how many Borda points does Candidate e
Receive? Who wins the Borda election?
A)48; b
B)55; b
C)184; e
D)59; e

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
37
Given the following voter profile, determine who has the majority of first place votes and then use the Borda Method to determine the outcome. Does the Borda method violate the majority criterion
For the voter profile?
For the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
38
Eighteen voters are using the Borda method to select one of four candidates: a, b, c, or d. If Candidate a receives 35 Borda points, Candidate b receives 28 Borda points, and Candidate c
Receives 20 Borda points, how many Borda points does Candidate d receive? Who wins the Borda
Election?
A)37; d
B)97; d
C)28; a
D)25; a
Receives 20 Borda points, how many Borda points does Candidate d receive? Who wins the Borda
Election?
A)37; d
B)97; d
C)28; a
D)25; a

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
39
Given the following voter profile, determine which candidate (if any)is a Condorcet Candidate and who will be selected using the Hare Method. Does the Hare Method violate the Condorcet criterion
For the voter profile?
For the voter profile?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
40
For the voter profile given below, who (or what)is selected if a runoff election is held between the candidates that rank second and third; and the winner of that election faces the candidate with the
Most first place votes, to decide the final outcome of the election?
Most first place votes, to decide the final outcome of the election?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
41
The Mathematics Department is holding an election for department chair. Each member ranks the candidates from first to third. The voter profile below shows the results of the preliminary
Nonbinding ballots with candidates Clark (C), Jones (J), and Smith (S).
Nonbinding ballots with candidates Clark (C), Jones (J), and Smith (S).


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
42
-Given that there are 30 voters and 4 candidates, complete the following voter profile so that the Borda Method violates the Majority Criterion.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
43
The preference table shows the results of an election among three candidates, A, B, and C.  (a)Using the plurality method, who is the winner? (b)The voters in the two columns on the right move their last-place candidates from last place to
(a)Using the plurality method, who is the winner? (b)The voters in the two columns on the right move their last-place candidates from last place to
First place. Construct a new preference table for the election. Using the table and the plurality
Method, who is the winner?
(c)Suppose that candidate C drops out of the new table, but the winner is still chosen by the
Plurality method. Is the irrelevant alternatives criterion satisfied?
A)A; A; no
B)A; A; yes
C)B; A; no
D)A; B; yes
 (a)Using the plurality method, who is the winner? (b)The voters in the two columns on the right move their last-place candidates from last place to
(a)Using the plurality method, who is the winner? (b)The voters in the two columns on the right move their last-place candidates from last place toFirst place. Construct a new preference table for the election. Using the table and the plurality
Method, who is the winner?
(c)Suppose that candidate C drops out of the new table, but the winner is still chosen by the
Plurality method. Is the irrelevant alternatives criterion satisfied?
A)A; A; no
B)A; A; yes
C)B; A; no
D)A; B; yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
44
In the following voter profile, use the Borda Method to determine the winner. If candidate d drops out, and a second election is held, who is the winner if the Borda Method is again used? Does the
Borda Method violate the Independence of Irrelevant Alternatives Criterion in this election
Process?
Borda Method violate the Independence of Irrelevant Alternatives Criterion in this election
Process?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Jefferson Method to apportion the computers.
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Jefferson Method to apportion the computers.


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Webster Method to apportion the seats.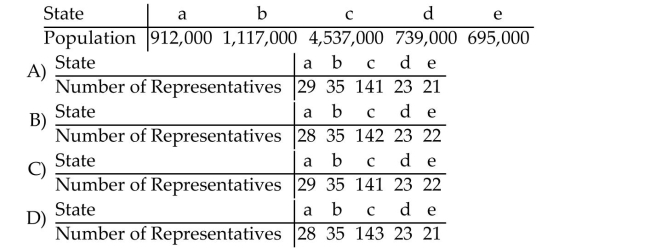
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Webster Method to apportion the seats.


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
47
Find the quantity requested. Round to the nearest whole number.
A total of 156 seats were apportioned to 19 states in a certain country which has a total population of 8,977,808. Find the average number of people represented per seat in this country.
A)57,550
B)472,516
C)3029
D)1,093,451
A total of 156 seats were apportioned to 19 states in a certain country which has a total population of 8,977,808. Find the average number of people represented per seat in this country.
A)57,550
B)472,516
C)3029
D)1,093,451

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
48
In the following voter profile, use the Pairwise Comparison Method to determine the winner. If candidate c drops out, and a second election is held, who is the winner if the Pairwise Comparison
Method is again used? Does the Pairwise Comparison Method violate the Independence of
Irrelevant Alternatives Criterion in this election process?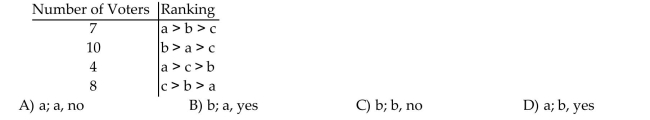
Method is again used? Does the Pairwise Comparison Method violate the Independence of
Irrelevant Alternatives Criterion in this election process?
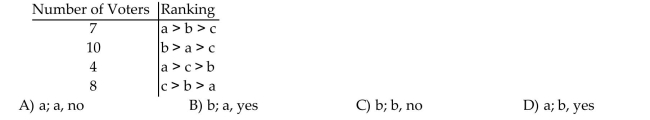

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
49
Find the quantity requested. Round to the nearest whole number.
A total of 280 seats were apportioned to 43 states in a certain country which has a total population of 24,853,749. Find the average number of seats assigned per state.
A)577,994
B)9
C)7
D)88,763
A total of 280 seats were apportioned to 43 states in a certain country which has a total population of 24,853,749. Find the average number of seats assigned per state.
A)577,994
B)9
C)7
D)88,763

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
50

Construct a voter profile for 41 voters and 4 candidates that has a Condorcet Candidate
that fails to be elected by both the Borda Method and the Hare Method.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
51
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees rank the four possible sites according to
The following voter profile:
The following voter profile:


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Jefferson Method to apportion the seats.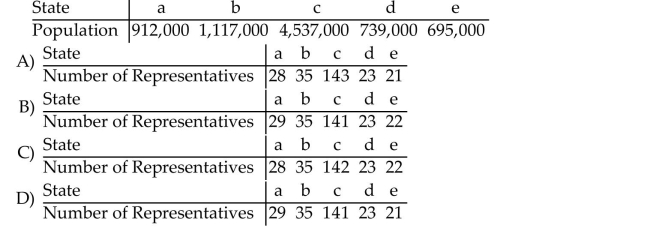
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Jefferson Method to apportion the seats.


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Hamilton Method to apportion the computers.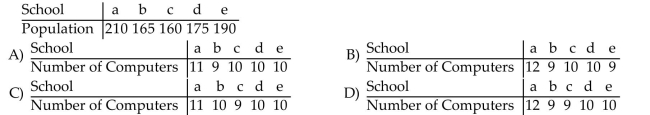
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Hamilton Method to apportion the computers.
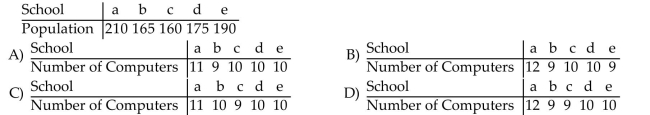

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
54

Suppose that one of the losing candidates is to be deleted from the given voter profile. Which choices would result in the plurality method violating the independence of irrelevant alternatives
Criterion in a second election?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
55

Construct a voter profile for 41 voters and 4 candidates that has a Condorcet Candidate
that fails to be elected by both the Borda Method and the Plurality Method.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
56
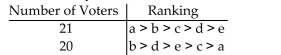
Given that there are 30 voters and 3 candidates, complete the following voter profile so
that the Borda Method violates the Majority Criterion.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
57
Construct a voter profile of 41 voters and 5 candidates where the Majority Candidate wins
4 pairwise comparison points and another candidate wins 3 pairwise points.
4 pairwise comparison points and another candidate wins 3 pairwise points.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
58
Computer Specialists is planning a group vacation to one of the following locations: Alaska (A), Florida (F), San Antonio (S), or Hawaii (H). The employees initially rank the four possible sites
According to the following voter profile:

According to the following voter profile:



Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Hamilton Method to apportion the seats.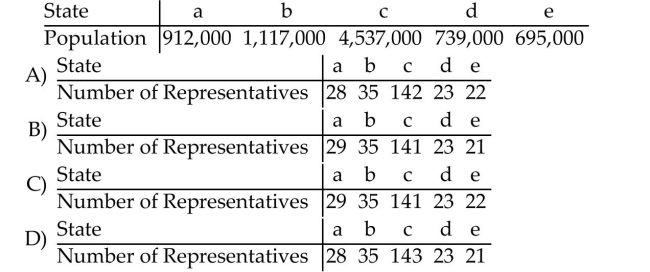
A country has five states with populations as given in the table below and needs to apportion 250 seats in the legislature. Use the Hamilton Method to apportion the seats.


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
60
In the following voter profile, use the Hare Method to determine the winner. If candidate d drops out, and a second election is held, who is the winner if the Hare Method is again used? Does the
Hare Method violate the Independence of Irrelevant Alternatives Criterion in this election process?
Hare Method violate the Independence of Irrelevant Alternatives Criterion in this election process?


Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.



Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
62
If the Jefferson Method is used to apportion 200 legislative seats to four states with the populations given in the table, then a violation of the Quota Rule occurs.
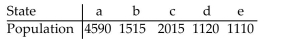 The apportionment for which state violates the Quota Rule?
The apportionment for which state violates the Quota Rule?A)e
B)d
C)b
D)a

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
63
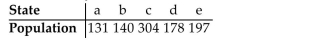
If the Hamilton Method is used to apportion legislative seats to two original states and a new state with the populations given in the table (in thousands), then one of the states loses a seat to another
If the original number of seats being apportioned is 48.
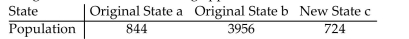 Which state loses a seat to which state, and does the New States paradox occur?
Which state loses a seat to which state, and does the New States paradox occur?A)b loses a seat to a, yes
B)b loses a seat to a, no
C)a loses a seat to b, no
D)a loses a seat to b, yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.



Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
65
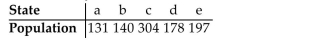
If the Hamilton Method is used to apportion legislative seats to three states with the initial and revised populations given in the table (in thousands), then one of the states loses a seat to another if
The number of seats being apportioned is 13.
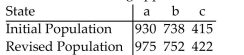 Which state loses a seat to which state, and does the Population Paradox occur?
Which state loses a seat to which state, and does the Population Paradox occur?A)a loses a seat to c, no
B)b loses a seat to c, yes
C)c loses a seat to a, no
D)c loses a seat to b, yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Webster Method to apportion the computers.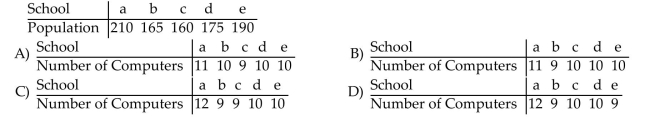
West End school district is purchasing 50 new computers to be distributed among the five schools in the district. The computers will be apportioned based on the school population of each school as
Given in the table below. Use the Webster Method to apportion the computers.
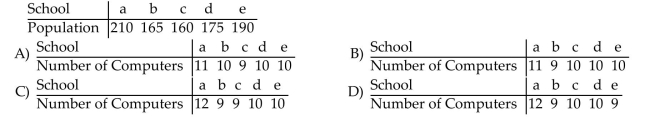

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
67
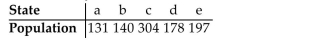
If the Hamilton Method is used to apportion legislative seats to four states with the populations given in the table, then the Alabama Paradox occurs when the number of seats being apportioned
Increases from 204 to 205.
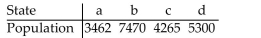 In which state does the paradox show up?
In which state does the paradox show up?A)c
B)d
C)b
D)a

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.



Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
69
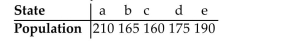
Create a population profile for 5 states with a total population of 8,000,000 for which the
Hamilton Method and Webster Method apportionments of 250 legislative seats are the
same, and the Jefferson Method apportionment is different.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
70
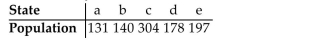
If the Hamilton Method is used to apportion legislative seats to five states with the populations given in the table, then the Alabama Paradox occurs when the number of seats being apportioned
Increases from 126 to 127.
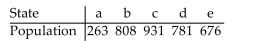 In which state does the paradox show up?
In which state does the paradox show up?A)d
B)c
C)b
D)a

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.



Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
72
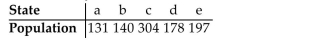
If the Hamilton Method is used to apportion legislative seats to three states with the initial and revised populations given in the table (in thousands), then one of the states loses a seat to another if
The number of seats being apportioned is 11.
 Which state loses a seat to which state, and does the Population Paradox occur?
Which state loses a seat to which state, and does the Population Paradox occur?A)c loses a seat to a, no
B)c loses a seat to a, yes
C)c loses a seat to b, yes
D)c loses a seat to b, no

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
73
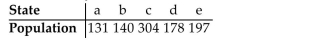
If the Hamilton Method is used to apportion legislative seats to two original states and a new state with the populations given in the table (in thousands), then one of the states loses a seat to another
If the original number of seats being apportioned is 100.
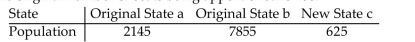 Which state loses a seat to which state, and does the New States paradox occur?
Which state loses a seat to which state, and does the New States paradox occur?A)b loses a seat to a, no
B)a loses a seat to b, yes
C)a loses a seat to b, no
D)b loses a seat to a, yes

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
74

Create a population profile for 5 states with a total population of 950 for which the
Hamilton Method, Jefferson Method, and Webster Method apportionments of 16
legislative seats are all different.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
75
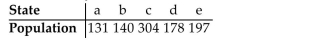
If the Jefferson Method is used to apportion 250 legislative seats to five states with the populations given in the table, then a violation of the Quota Rule occurs.
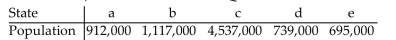 The apportionment for which state violates the Quota Rule?
The apportionment for which state violates the Quota Rule?A)b
B)e
C)c
D)a

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
76
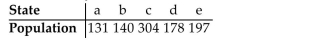
If the Hamilton Method is used to apportion legislative seats to three states with the initial and revised populations given in the table, then one of the states loses a seat to another if the number of
Seats being apportioned is 100.
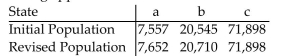 Which state loses a seat to which state, and does the Population Paradox occur?
Which state loses a seat to which state, and does the Population Paradox occur?A)a loses a seat to b, yes
B)b loses a seat to a, no
C)b loses a seat to a, yes
D)a loses a seat to b, no

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
77
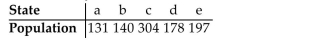
If the Jefferson Method is used to apportion 132 legislative seats to four states with the populations given in the table, then a violation of the Quota Rule occurs.
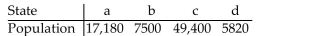 The apportionment for which state violates the Quota Rule?
The apportionment for which state violates the Quota Rule?A)c
B)b
C)a
D)d

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
Create a population profile for 5 states with a total population of 900 for which the
Hamilton Method, Jefferson Method, and Webster Method apportionments of 50
legislative seats all agree.
Create a population profile for 5 states with a total population of 900 for which the
Hamilton Method, Jefferson Method, and Webster Method apportionments of 50
legislative seats all agree.

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
79
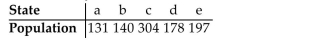
If the Jefferson Method is used to apportion 131 legislative seats to six states with the populations given in the table, then a violation of the Quota Rule occurs.
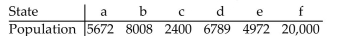 The apportionment for which state violates the Quota Rule?
The apportionment for which state violates the Quota Rule?A)e
B)b
C)d
D)f

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck
80
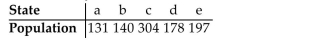
If the Hamilton Method is used to apportion legislative seats to three states with the populations given in the table, then the Alabama Paradox occurs when the number of seats being apportioned
Increases from 150 to 151.
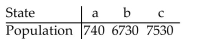 In which state does the paradox show up?
In which state does the paradox show up?A)a
B)c
C)b

Unlock Deck
Unlock for access to all 99 flashcards in this deck.
Unlock Deck
k this deck


