Deck 7: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/62
Play
Full screen (f)
Deck 7: Sampling Distributions
1
Which of the following is true about the sampling distribution of the sample mean?
A) The mean of the sampling distribution is always
B) The standard deviation of the sampling distribution is always
C) The shape of the sampling distribution is always approximately normal.
D) All of the above are true.
A) The mean of the sampling distribution is always

B) The standard deviation of the sampling distribution is always

C) The shape of the sampling distribution is always approximately normal.
D) All of the above are true.
A
2
Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players exceeded $4.0 million.
A) Approximately 0
B) 0.0228
C) 0.9772
D) Approximately 1
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players exceeded $4.0 million.
A) Approximately 0
B) 0.0228
C) 0.9772
D) Approximately 1
A
3
If the expected value of a sample statistic is equal to the parameter it is estimating, then we call
That sample statistic
A) unbiased.
B) minimum variance.
C) biased.
D) random.
That sample statistic
A) unbiased.
B) minimum variance.
C) biased.
D) random.
A
4
True or False: The amount of time it takes to complete an examination has a left skewed
distribution with a mean of 65 minutes and a standard deviation of 8 minutes.If 64 students were
randomly sampled, the probability that the sample mean of the sampled students exceeds 71
minutes is approximately 0.
distribution with a mean of 65 minutes and a standard deviation of 8 minutes.If 64 students were
randomly sampled, the probability that the sample mean of the sampled students exceeds 71
minutes is approximately 0.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
5
Sales prices of baseball cards from the 1960s are known to possess a right skewed distribution
With a mean sale price of $5.25 and a standard deviation of $2.80.Suppose a random sample of
100 cards from the 1960s is selected.Describe the sampling distribution for the sample mean sale
Price of the selected cards.
A) Right skewed with a mean of $5.25 and a standard error of $2.80
B) Normal with a mean of $5.25 and a standard error of $0.28
C) Right skewed with a mean of $5.25 and a standard error of $0.28
D) Normal with a mean of $5.25 and a standard error of $2.80
With a mean sale price of $5.25 and a standard deviation of $2.80.Suppose a random sample of
100 cards from the 1960s is selected.Describe the sampling distribution for the sample mean sale
Price of the selected cards.
A) Right skewed with a mean of $5.25 and a standard error of $2.80
B) Normal with a mean of $5.25 and a standard error of $0.28
C) Right skewed with a mean of $5.25 and a standard error of $0.28
D) Normal with a mean of $5.25 and a standard error of $2.80

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
6
The Central Limit Theorem is important in statistics because
A) for a large n, it says the population is approximately normal.
B) for any population, it says the sampling distribution of the sample mean is approximately normal, regardless of the sample size.
C) for a large n, it says the sampling distribution of the sample mean is approximately normal, regardless of the shape of the population.
D) for any sized sample, it says the sampling distribution of the sample mean is approximately normal.
A) for a large n, it says the population is approximately normal.
B) for any population, it says the sampling distribution of the sample mean is approximately normal, regardless of the sample size.
C) for a large n, it says the sampling distribution of the sample mean is approximately normal, regardless of the shape of the population.
D) for any sized sample, it says the sampling distribution of the sample mean is approximately normal.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
7
True or False: The Central Limit Theorem is considered powerful in statistics because it works
for any population distribution provided the sample size is sufficiently large and the population
mean and standard deviation are known.
for any population distribution provided the sample size is sufficiently large and the population
mean and standard deviation are known.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
8
A sample that does not provide a good representation of the population from which it was
collected is referred to as a(n)sample.
collected is referred to as a(n)sample.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following statements about the sampling distribution of the sample mean is
Incorrect?
A) The sampling distribution of the sample mean is approximately normal whenever the sample size is sufficiently large
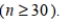
B) The sampling distribution of the sample mean is generated by repeatedly taking samples of size n and computing the sample means.
C) The mean of the sampling distribution of the sample mean is equal to μ.
D) The standard deviation of the sampling distribution of the sample mean is equal to σ.
Incorrect?
A) The sampling distribution of the sample mean is approximately normal whenever the sample size is sufficiently large
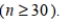
B) The sampling distribution of the sample mean is generated by repeatedly taking samples of size n and computing the sample means.
C) The mean of the sampling distribution of the sample mean is equal to μ.
D) The standard deviation of the sampling distribution of the sample mean is equal to σ.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
10
Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players was no more than $3.0 million.
A) Approximately 0
B) 0.0151
C) 0.9849
D) Approximately 1
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players was no more than $3.0 million.
A) Approximately 0
B) 0.0151
C) 0.9849
D) Approximately 1

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
11
Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in
A certain year in the past.Suppose a sample of 100 major league players was taken.What was the
Standard error for the sample mean salary?
A) $0.012 million
B) $0.12 million
C) $12 million
D) $1,200.0 million
A certain year in the past.Suppose a sample of 100 major league players was taken.What was the
Standard error for the sample mean salary?
A) $0.012 million
B) $0.12 million
C) $12 million
D) $1,200.0 million

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
12
The standard error of the mean
A) is never larger than the standard deviation of the population.
B) decreases as the sample size increases.
C) measures the variability of the mean from sample to sample.
D) All of the above.
A) is never larger than the standard deviation of the population.
B) decreases as the sample size increases.
C) measures the variability of the mean from sample to sample.
D) All of the above.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
13
 .
.
Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
14
Why is the Central Limit Theorem so important to the study of sampling distributions?
A) It allows us to disregard the size of the sample selected when the population is not normal.
B) It allows us to disregard the shape of the sampling distribution when the size of the population is large.
C) It allows us to disregard the size of the population we are sampling from.
D) It allows us to disregard the shape of the population when n is large.
A) It allows us to disregard the size of the sample selected when the population is not normal.
B) It allows us to disregard the shape of the sampling distribution when the size of the population is large.
C) It allows us to disregard the size of the population we are sampling from.
D) It allows us to disregard the shape of the population when n is large.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
15
The distribution of the number of loaves of bread sold per week by a large bakery over the past 5
years has a mean of 7,750 and a standard deviation of 145 loaves.Suppose a random sample of n
= 40 weeks has been selected.What is the approximate probability that the mean number of
loaves sold in the sampled weeks exceeds 7,895 loaves?
years has a mean of 7,750 and a standard deviation of 145 loaves.Suppose a random sample of n
= 40 weeks has been selected.What is the approximate probability that the mean number of
loaves sold in the sampled weeks exceeds 7,895 loaves?

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
16
Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players exceeded $3.5 million.
A) Approximately 0
B) 0.0228
C) 0.9772
D) Approximately 1
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players exceeded $3.5 million.
A) Approximately 0
B) 0.0228
C) 0.9772
D) Approximately 1

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
17
Major league baseball salaries averaged $3.26 million with a standard deviation of $1.2 million in
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players was less than $2.5 million.
A) Approximately 0
B) 0.0151
C) 0.9849
D) Approximately 1
A certain year in the past.Suppose a sample of 100 major league players was taken.Find the
Approximate probability that the mean salary of the 100 players was less than $2.5 million.
A) Approximately 0
B) 0.0151
C) 0.9849
D) Approximately 1

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose the ages of students in Statistics 101 follow a right skewed distribution with a mean of
23 years and a standard deviation of 3 years.If we randomly sampled 100 students, which of the
Following statements about the sampling distribution of the sample mean age is incorrect?
A) The mean of the sampling distribution is equal to 23 years.
B) The standard deviation of the sampling distribution is equal to 3 years.
C) The shape of the sampling distribution is approximately normal.
D) The standard error of the sampling distribution is equal to 0.3 years.
23 years and a standard deviation of 3 years.If we randomly sampled 100 students, which of the
Following statements about the sampling distribution of the sample mean age is incorrect?
A) The mean of the sampling distribution is equal to 23 years.
B) The standard deviation of the sampling distribution is equal to 3 years.
C) The shape of the sampling distribution is approximately normal.
D) The standard error of the sampling distribution is equal to 0.3 years.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
19
Sampling distributions describe the distribution of
A) parameters.
B) statistics.
C) both parameters and statistics.
D) neither parameters nor statistics.
A) parameters.
B) statistics.
C) both parameters and statistics.
D) neither parameters nor statistics.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
20
For air travelers, one of the biggest complaints is of the waiting time between when the airplane
Taxis away from the terminal until the flight takes off.This waiting time is known to have a right
Skewed distribution with a mean of 10 minutes and a standard deviation of 8 minutes.Suppose
100 flights have been randomly sampled.Describe the sampling distribution of the mean waiting
Time between when the airplane taxis away from the terminal until the flight takes off for these
100 flights.
A) Distribution is right skewed with mean = 10 minutes and standard error = 0.8 minutes.
B) Distribution is right skewed with mean = 10 minutes and standard error = 8 minutes.
C) Distribution is approximately normal with mean = 10 minutes and standard error = 0.8 minutes.
D) Distribution is approximately normal with mean = 10 minutes and standard error = 8 minutes.
Taxis away from the terminal until the flight takes off.This waiting time is known to have a right
Skewed distribution with a mean of 10 minutes and a standard deviation of 8 minutes.Suppose
100 flights have been randomly sampled.Describe the sampling distribution of the mean waiting
Time between when the airplane taxis away from the terminal until the flight takes off for these
100 flights.
A) Distribution is right skewed with mean = 10 minutes and standard error = 0.8 minutes.
B) Distribution is right skewed with mean = 10 minutes and standard error = 8 minutes.
C) Distribution is approximately normal with mean = 10 minutes and standard error = 0.8 minutes.
D) Distribution is approximately normal with mean = 10 minutes and standard error = 8 minutes.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
21
The owner of a fish market has an assistant who has determined that the weights of catfish are
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
16 fish is taken, what would the standard error of the mean weight equal?
A) 0.003
B) 0.050
C) 0.200
D) 0.800
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
16 fish is taken, what would the standard error of the mean weight equal?
A) 0.003
B) 0.050
C) 0.200
D) 0.800

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
22
The owner of a fish market has an assistant who has determined that the weights of catfish are
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
64 fish yields a mean of 3.4 pounds, what is probability of obtaining a sample mean this large or
Larger?
A) 0.0001
B) 0.0013
C) 0.0228
D) 0.4987
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
64 fish yields a mean of 3.4 pounds, what is probability of obtaining a sample mean this large or
Larger?
A) 0.0001
B) 0.0013
C) 0.0228
D) 0.4987

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
23
The owner of a fish market has an assistant who has determined that the weights of catfish are
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.What
Percentage of samples of 4 fish will have sample means between 3.0 and 4.0 pounds?
A) 84%
B) 67%
C) 29%
D) 16%
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.What
Percentage of samples of 4 fish will have sample means between 3.0 and 4.0 pounds?
A) 84%
B) 67%
C) 29%
D) 16%

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
24
True or False: As the sample size increases, the effect of an extreme value on the sample mean
becomes smaller.
becomes smaller.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
25
True or False: If the population distribution is skewed, in most cases the sampling distribution
of the mean can be approximated by the normal distribution if the samples contain at least 30
observations.
of the mean can be approximated by the normal distribution if the samples contain at least 30
observations.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
26
True or False: If the population distribution is unknown, in most cases the sampling distribution
of the mean can be approximated by the normal distribution if the samples contain at least 30
observations.
of the mean can be approximated by the normal distribution if the samples contain at least 30
observations.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
27
True or False: If the population distribution is symmetric, the sampling distribution of the mean
can be approximated by the normal distribution if the samples contain 15 observations.
can be approximated by the normal distribution if the samples contain 15 observations.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
28
True or False: If the amount of gasoline purchased per car at a large service station has a
population mean of 15 gallons and a population standard deviation of 4 gallons and a random
sample of 4 cars is selected, there is approximately a 68.26% chance that the sample mean will be
between 13 and 17 gallons.
population mean of 15 gallons and a population standard deviation of 4 gallons and a random
sample of 4 cars is selected, there is approximately a 68.26% chance that the sample mean will be
between 13 and 17 gallons.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
29
The standard error of the population proportion will become larger
A) as population proportion approaches 0.
B) as population proportion approaches 0.50.
C) as population proportion approaches 1.00.
D) as the sample size increases.
A) as population proportion approaches 0.
B) as population proportion approaches 0.50.
C) as population proportion approaches 1.00.
D) as the sample size increases.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
30
For sample size 1, the sampling distribution of the mean will be normally distributed
A) regardless of the shape of the population.
B) only if the shape of the population is symmetrical.
C) only if the population values are positive.
D) only if the population is normally distributed.
A) regardless of the shape of the population.
B) only if the shape of the population is symmetrical.
C) only if the population values are positive.
D) only if the population is normally distributed.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
31
The owner of a fish market has an assistant who has determined that the weights of catfish are
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
25 fish yields a mean of 3.6 pounds, what is the Z-score for this observation?
A) 18.750
B) 2.500
C) 1.875
D) 0.750
Normally distributed, with mean of 3.2 pounds and standard deviation of 0.8 pound.If a sample of
25 fish yields a mean of 3.6 pounds, what is the Z-score for this observation?
A) 18.750
B) 2.500
C) 1.875
D) 0.750

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
32
True or False: A sampling distribution is a distribution for a statistic.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
33
True or False: If the amount of gasoline purchased per car at a large service station has a
population mean of 15 gallons and a population standard deviation of 4 gallons and it is assumed
that the amount of gasoline purchased per car is symmetric, there is approximately a 68.26%
chance that a random sample of 16 cars will have a sample mean between 14 and 16 gallons.
population mean of 15 gallons and a population standard deviation of 4 gallons and it is assumed
that the amount of gasoline purchased per car is symmetric, there is approximately a 68.26%
chance that a random sample of 16 cars will have a sample mean between 14 and 16 gallons.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
34
The standard error of the mean for a sample of 100 is 30.In order to cut the standard error of the
Mean to 15, we would
A) increase the sample size to 200.
B) increase the sample size to 400.
C) decrease the sample size to 50.
D) decrease the sample to 25.
Mean to 15, we would
A) increase the sample size to 200.
B) increase the sample size to 400.
C) decrease the sample size to 50.
D) decrease the sample to 25.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
35
For sample sizes greater than 30, the sampling distribution of the mean will be approximately
Normally distributed
A) regardless of the shape of the population.
B) only if the shape of the population is symmetrical.
C) only if the standard deviation of the samples are known.
D) only if the population is normally distributed.
Normally distributed
A) regardless of the shape of the population.
B) only if the shape of the population is symmetrical.
C) only if the standard deviation of the samples are known.
D) only if the population is normally distributed.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
36
For sample size 16, the sampling distribution of the mean will be approximately normally
Distributed
A) regardless of the shape of the population.
B) if the shape of the population is symmetrical.
C) if the sample standard deviation is known.
D) if the sample is normally distributed.
Distributed
A) regardless of the shape of the population.
B) if the shape of the population is symmetrical.
C) if the sample standard deviation is known.
D) if the sample is normally distributed.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
37
True or False: If the amount of gasoline purchased per car at a large service station has a
population mean of 15 gallons and a population standard deviation of 4 gallons, then 99.73% of
all cars will purchase between 3 and 27 gallons.
population mean of 15 gallons and a population standard deviation of 4 gallons, then 99.73% of
all cars will purchase between 3 and 27 gallons.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
38
True or False: As the sample size increases, the standard error of the mean increases.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following is true regarding the sampling distribution of the mean for a large sample
Size?
A) It has the same shape, mean, and standard deviation as the population.
B) It has a normal distribution with the same mean and standard deviation as the population.
C) It has the same shape and mean as the population, but has a smaller standard deviation.
D) It has a normal distribution with the same mean as the population but with a smaller standard deviation.
Size?
A) It has the same shape, mean, and standard deviation as the population.
B) It has a normal distribution with the same mean and standard deviation as the population.
C) It has the same shape and mean as the population, but has a smaller standard deviation.
D) It has a normal distribution with the same mean as the population but with a smaller standard deviation.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
40
True or False: If the amount of gasoline purchased per car at a large service station has a
population mean of 15 gallons and a population standard deviation of 4 gallons and a random
sample of 64 cars is selected, there is approximately a 95.44% chance that the sample mean will
be between 14 and 16 gallons.
population mean of 15 gallons and a population standard deviation of 4 gallons and a random
sample of 64 cars is selected, there is approximately a 95.44% chance that the sample mean will
be between 14 and 16 gallons.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
41


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
42
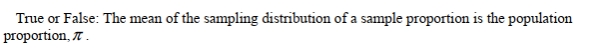

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
43
True or False: The amount of bleach a machine pours into bottles has a mean of 36 oz.with a
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean has a standard error of 0.15.
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean has a standard error of 0.15.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
44
True or False: The fact that the sample means are less variable than the population data can be
observed from the standard error of the mean.
observed from the standard error of the mean.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
45
True or False: The Central Limit Theorem ensures that the sampling distribution of the sample
mean approaches a normal distribution as the sample size increases.
mean approaches a normal distribution as the sample size increases.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
46
True or False: As the size of the sample is increased, the standard deviation of the sampling
distribution of the sample mean for a normally distributed population will stay the same.
distribution of the sample mean for a normally distributed population will stay the same.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
47
True or False: In inferential statistics, the standard error of the sample mean assesses the
uncertainty or error of estimation.
uncertainty or error of estimation.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
48
True or False: Suppose μ = 50 and σ = 10 for a population.In a sample where n = 100 is
randomly taken, 95% of all possible sample means will fall between 48.04 and 51.96.
randomly taken, 95% of all possible sample means will fall between 48.04 and 51.96.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
49
True or False: The sample mean is an unbiased estimate of the population mean.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
50
True or False: An unbiased estimator will have a value, on average across samples, equal to the
population parameter value.
population parameter value.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
51


Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
52
True or False: For distributions such as the normal distribution, the arithmetic mean is
considered more stable from sample to sample than other measures of central tendency.
considered more stable from sample to sample than other measures of central tendency.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
53
True or False: A sampling distribution is defined as the probability distribution of possible
sample sizes that can be observed from a given population.
sample sizes that can be observed from a given population.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
54
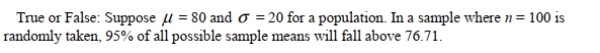

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
55
True or False: A sample of size 25 provides a sample variance of 400.The standard error, in
this case equal to 4, is best described as the estimate of the standard deviation of means calculated
from samples of size 25.
this case equal to 4, is best described as the estimate of the standard deviation of means calculated
from samples of size 25.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
56
True or False: The amount of bleach a machine pours into bottles has a mean of 36 oz.with a
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean has a mean of 36 oz.
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean has a mean of 36 oz.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
57
True or False: The sample proportion is an unbiased estimate of the population proportion.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
58

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
59
True or False: The standard error of the mean is also known as the standard deviation of the
sampling distribution of the sample mean.
sampling distribution of the sample mean.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
60
True or False: The amount of bleach a machine pours into bottles has a mean of 36 oz.with a
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean will be approximately normal only if the
population sampled is normal.
standard deviation of 0.15 oz.Suppose we take a random sample of 36 bottles filled by this
machine.The sampling distribution of the sample mean will be approximately normal only if the
population sampled is normal.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
61
True or False: The sample proportion is an unbiased estimator for the population proportion.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck
62
True or False: The sample mean is an unbiased estimator for the population mean.

Unlock Deck
Unlock for access to all 62 flashcards in this deck.
Unlock Deck
k this deck


