Deck 9: Analytic Geometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/197
Play
Full screen (f)
Deck 9: Analytic Geometry
1
Match the equation to its graph.
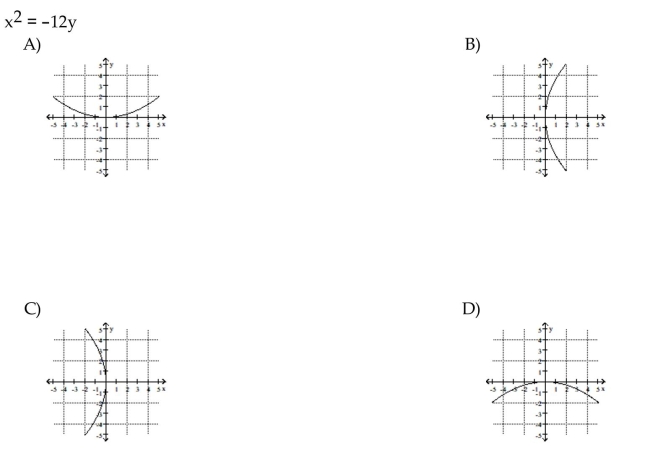

D
2
Graph the equation.





A
3
Graph the equation.
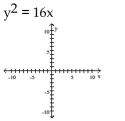





D
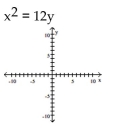
4
Match the equation to its graph.
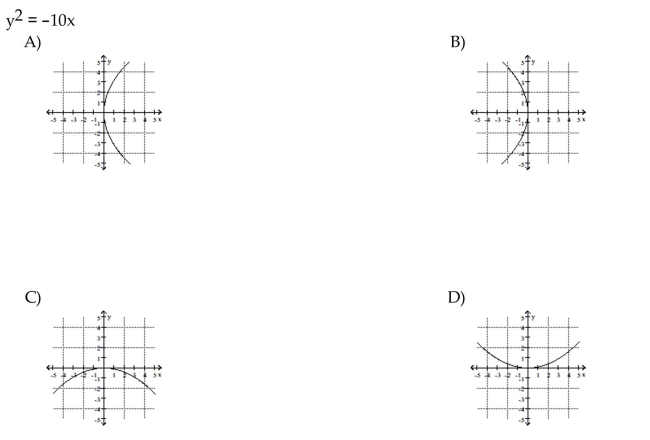


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
5
Find an equation of the parabola described.
Focus at (0, 21); directrix the line y = -21
Focus at (0, 21); directrix the line y = -21


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
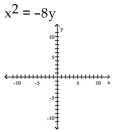
6
Find the vertex, focus, and directrix of the parabola.






Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
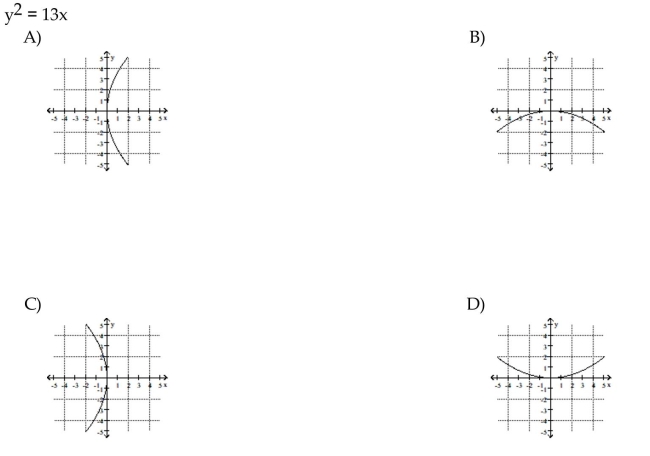
7
Match the equation to its graph.


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
8
Find an equation of the parabola described.
Focus at (5, 0); vertex at (0, 0)
Focus at (5, 0); vertex at (0, 0)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
9
Find an equation of the parabola described.
Directrix the line y = 3; vertex at (0, 0)
Directrix the line y = 3; vertex at (0, 0)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
10
Find an equation of the parabola described.
Focus at (-3, 0); directrix the line x = 3
Focus at (-3, 0); directrix the line x = 3


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
11
Name the conic.

A) circle
B) hyperbola
C) ellipse
D) parabola

A) circle
B) hyperbola
C) ellipse
D) parabola

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
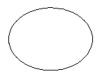
12
Name the conic.
A) circle
B) ellipse
C) hyperbola
D) parabola

A) circle
B) ellipse
C) hyperbola
D) parabola

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
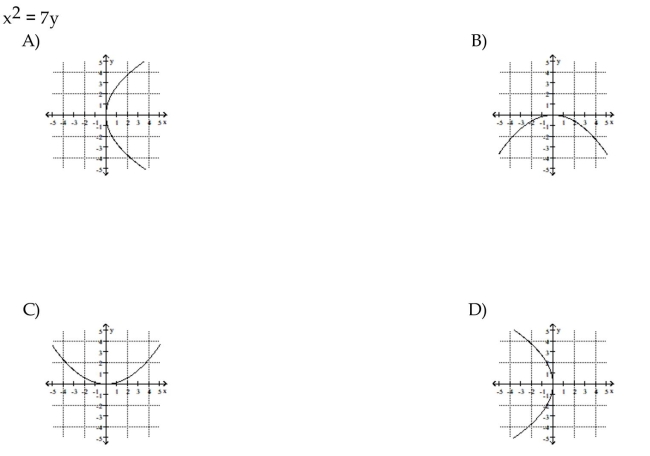
13
Match the equation to its graph.


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
14
Find an equation of the parabola described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
15
Name the conic.
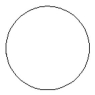
A) circle
B) parabola
C) hyperbola
D) ellipse

A) circle
B) parabola
C) hyperbola
D) ellipse

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
16
Find an equation of the parabola described.
Vertex at (0, 0); axis of symmetry the x-axis; containing the point (9, 5)
Vertex at (0, 0); axis of symmetry the x-axis; containing the point (9, 5)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
17
Name the conic.
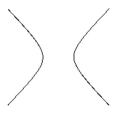
A) parabola
B) circle
C) hyperbola
D) ellipse

A) parabola
B) circle
C) hyperbola
D) ellipse

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
18
Find an equation of the parabola described and state the two points that define the latus rectum.
Focus at (0, 4); directrix the line y = -4
Focus at (0, 4); directrix the line y = -4


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
19
Graph the equation.
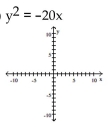






Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
20
Find the vertex, focus, and directrix of the parabola.
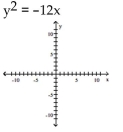






Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
21
Match the equation to the graph.
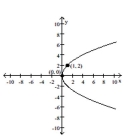




Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
22
Write an equation for the parabola.
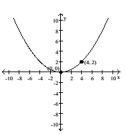




Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
23
Graph the equation.
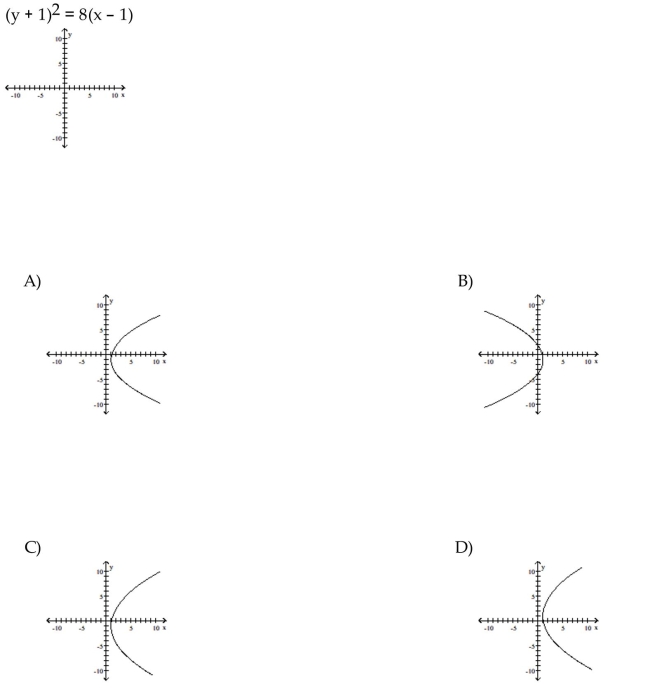


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
24
Match the equation to the graph.
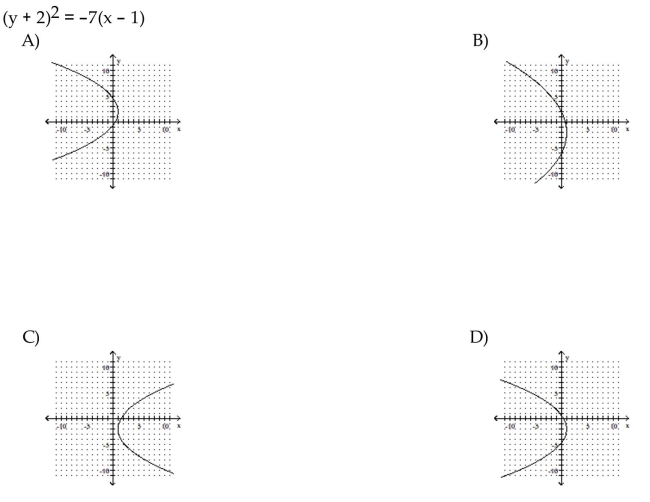


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
25
Find the vertex, focus, and directrix of the parabola. Graph the equation.
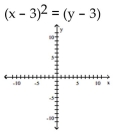
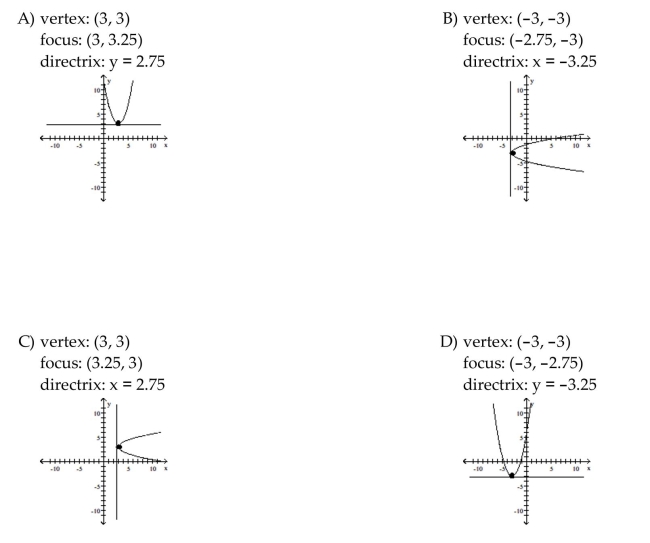



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
26
Find the vertex, focus, and directrix of the parabola. Graph the equation.
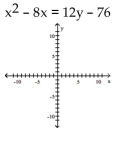
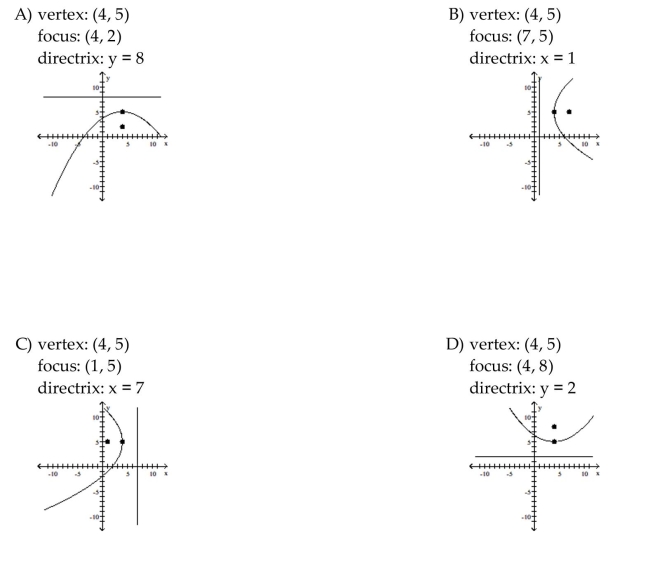



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
27
Find the vertex, focus, and directrix of the parabola. Graph the equation.
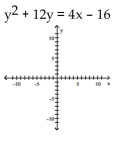



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
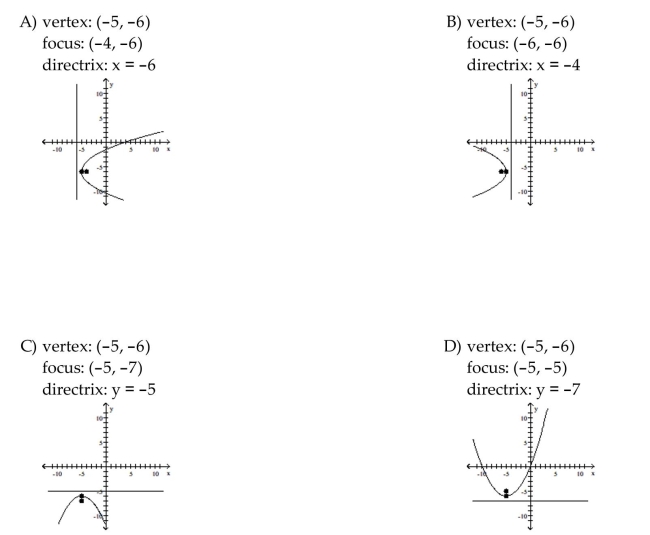
28
Match the equation to the graph.


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
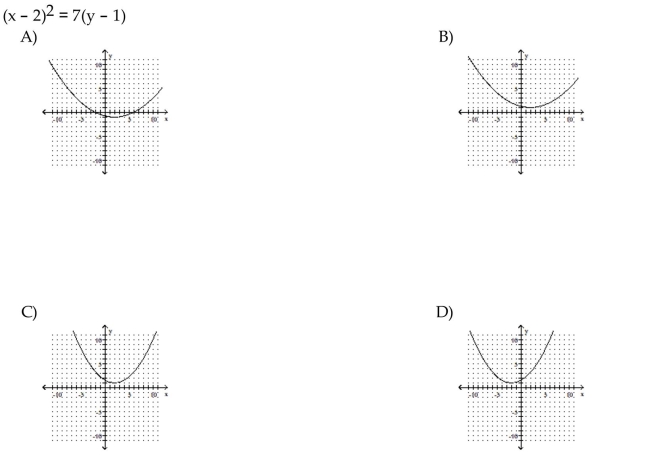
29
Find the vertex, focus, and directrix of the parabola with the given equation.
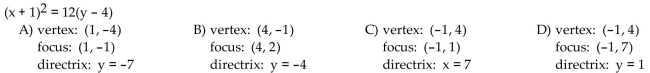
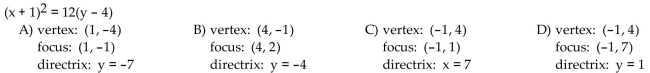

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
30
Find an equation for the parabola described.
Vertex at (6, 1); focus at (6, 3)
Vertex at (6, 1); focus at (6, 3)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
31
Find an equation for the parabola described.
Vertex at (3, -4); focus at (3, -6)
Vertex at (3, -4); focus at (3, -6)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
32
Find the vertex, focus, and directrix of the parabola. Graph the equation.
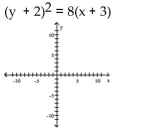
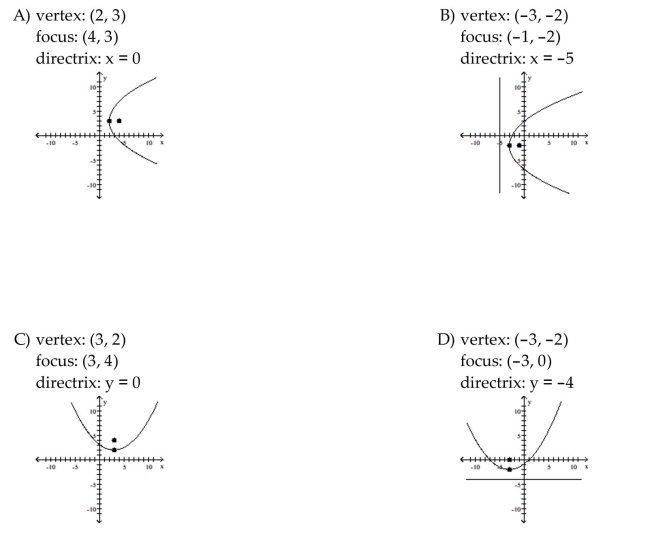



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
33
Find the vertex, focus, and directrix of the parabola with the given equation.
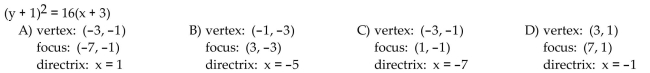
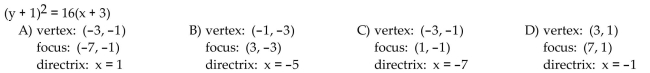

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
34
Find an equation for the parabola described.
Vertex at (7, 8); focus at (3, 8)
Vertex at (7, 8); focus at (3, 8)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
35
Find an equation for the parabola described.
Vertex at (7, -9); focus at (3, -9)
Vertex at (7, -9); focus at (3, -9)


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
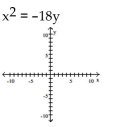
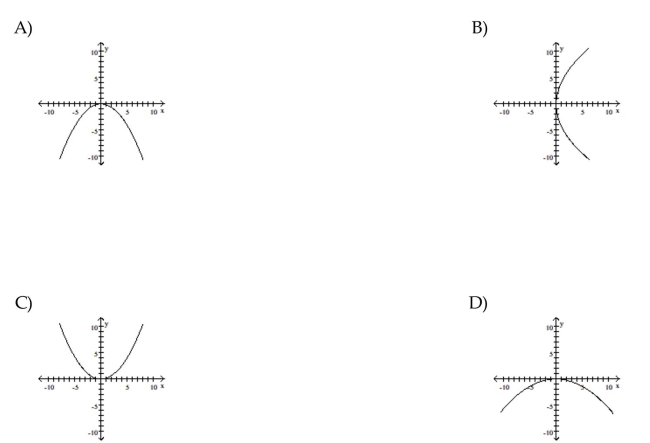
36
Graph the equation.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
37
Find the vertex, focus, and directrix of the parabola with the given equation.
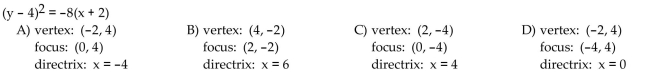
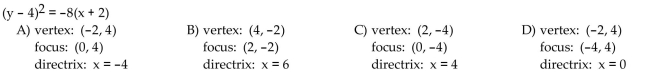

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
38
Match the equation to the graph.





Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
39
Match the equation to the graph.
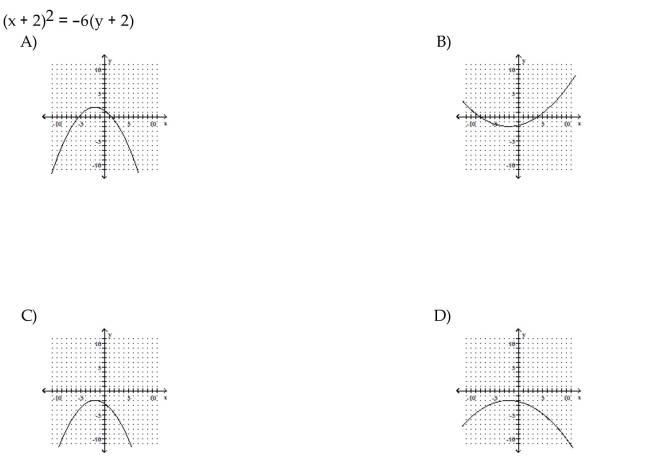


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
40
Find the vertex, focus, and directrix of the parabola with the given equation.
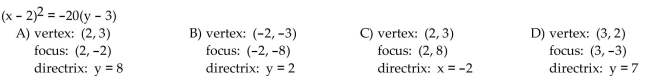
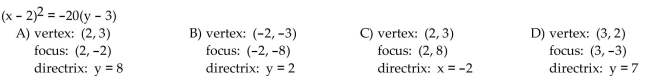

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
A satellite dish is shaped like a paraboloid of revolution. The signals that emanate from a satellite strike the
surface of the dish and are reflected to a single point, where the receiver is located. If the dish is 8 feet across at
its opening and is 2 feet deep at its center, at what position should the receiver be placed?
A satellite dish is shaped like a paraboloid of revolution. The signals that emanate from a satellite strike the
surface of the dish and are reflected to a single point, where the receiver is located. If the dish is 8 feet across at
its opening and is 2 feet deep at its center, at what position should the receiver be placed?

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
A spotlight has a parabolic cross section that is 6 ft wide at the opening and 2.5 ft deep at the vertex. How far from the vertex is the focus? Round answer to two decimal places.
A) 0.21 ft
B) 0.52 ft
C) 0.26 ft
D) 0.90 ft
A spotlight has a parabolic cross section that is 6 ft wide at the opening and 2.5 ft deep at the vertex. How far from the vertex is the focus? Round answer to two decimal places.
A) 0.21 ft
B) 0.52 ft
C) 0.26 ft
D) 0.90 ft

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
43
Graph the equation.
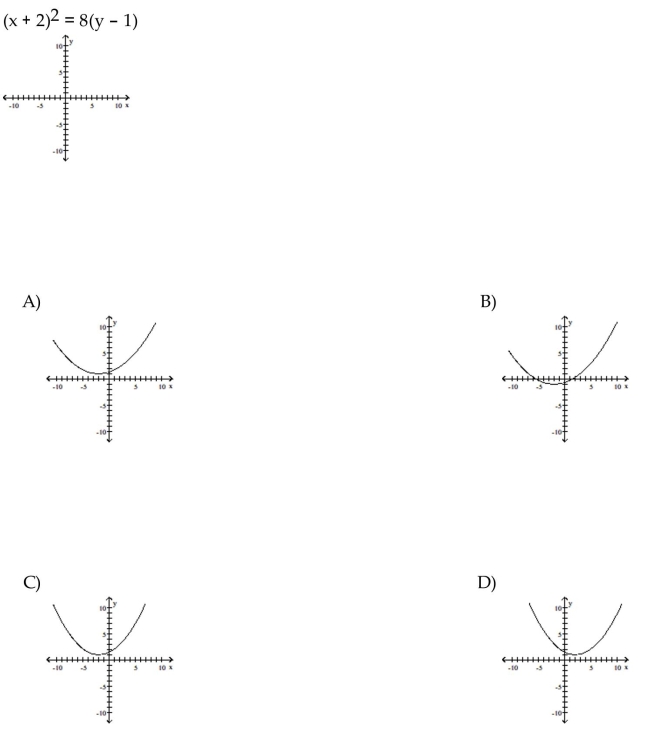


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
44
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
45
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
46
Match the graph to its equation.
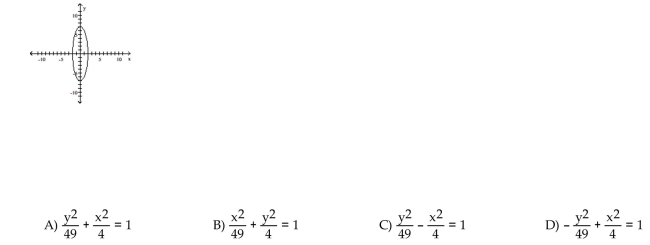
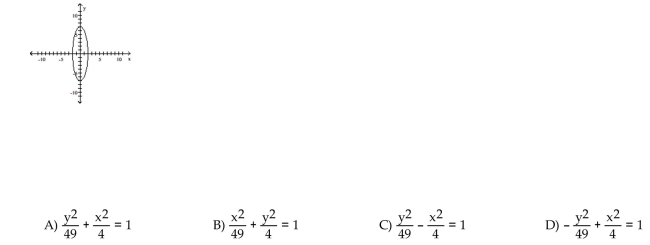

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is
3 centimeters from the vertex. If the depth is to be 6 centimeters, what is the diameter of the headlight at its
opening?
A sealed-beam headlight is in the shape of a paraboloid of revolution. The bulb, which is placed at the focus, is
3 centimeters from the vertex. If the depth is to be 6 centimeters, what is the diameter of the headlight at its
opening?

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
48
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
49
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
A reflecting telescope contains a mirror shaped like a paraboloid of revolution. If the mirror is 24 inches across at its opening and is 4 feet deep, where will the light be concentrated?
A) 0.1 in. from the vertex
B) 10.1 in. from the vertex
C) 0.2 in. from the vertex
D) 0.8 in. from the vertex
A reflecting telescope contains a mirror shaped like a paraboloid of revolution. If the mirror is 24 inches across at its opening and is 4 feet deep, where will the light be concentrated?
A) 0.1 in. from the vertex
B) 10.1 in. from the vertex
C) 0.2 in. from the vertex
D) 0.8 in. from the vertex

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
51
Match the graph to its equation.
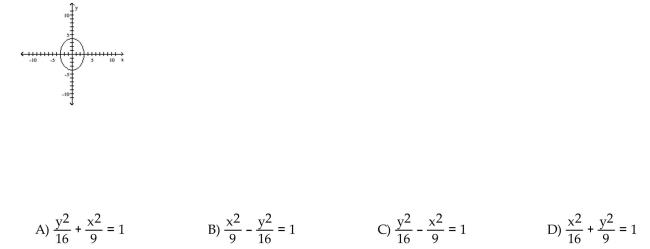
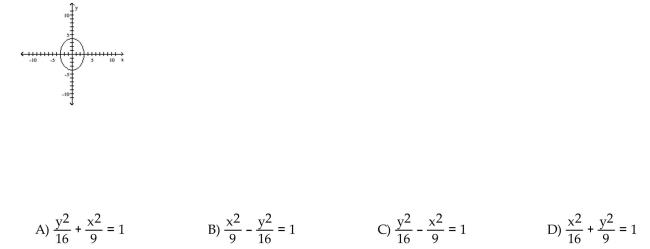

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
52
Find the center, foci, and vertices of the ellipse.
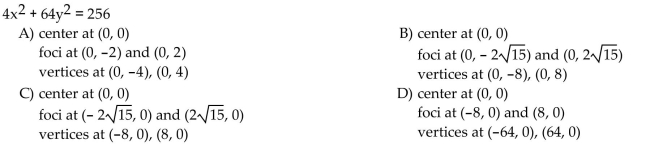
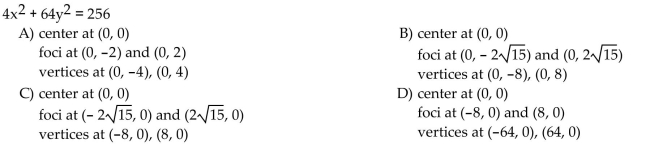

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
A searchlight is shaped like a paraboloid of revolution. If the light source is located 5 feet from the base along the axis of symmetry and the opening is 8 feet across, how deep should the searchlight be?
A) 4 ft
B) 0.8 ft
C) 1.6 ft
D) 3.2 ft
A searchlight is shaped like a paraboloid of revolution. If the light source is located 5 feet from the base along the axis of symmetry and the opening is 8 feet across, how deep should the searchlight be?
A) 4 ft
B) 0.8 ft
C) 1.6 ft
D) 3.2 ft

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the equation.
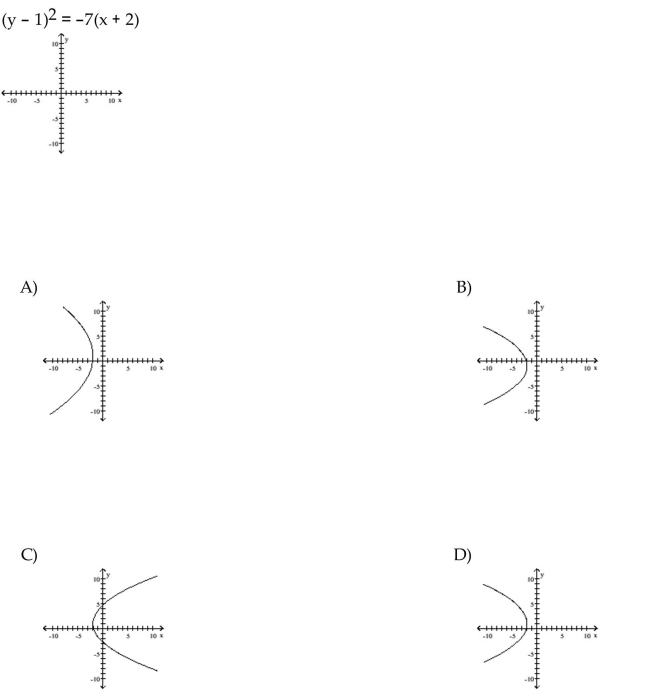


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers stand 50 inches apart. At a point between the towers and 15 inches along the road from the
Base of one tower, the cable is 1 inches above the roadway. Find the height of the towers.
A) 6.75 in.
B) 5.75 in.
C) 6.25 in.
D) 8.25 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers stand 50 inches apart. At a point between the towers and 15 inches along the road from the
Base of one tower, the cable is 1 inches above the roadway. Find the height of the towers.
A) 6.75 in.
B) 5.75 in.
C) 6.25 in.
D) 8.25 in.

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. Find the vertical distance from the
Roadway to the cable at a point on the road 14 inches from the lowest point of the cable.
A) 2.16 in.
B) 1.76 in.
C) 7.84 in.
D) 1.96 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. Find the vertical distance from the
Roadway to the cable at a point on the road 14 inches from the lowest point of the cable.
A) 2.16 in.
B) 1.76 in.
C) 7.84 in.
D) 1.96 in.

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 174 feet and a maximum height of 30 feet. Find the height of the arch at 15 feet from its center.
A) 3.6 ft
B) 21.8 ft
C) 0.2 ft
D) 29.1 ft
A bridge is built in the shape of a parabolic arch. The bridge arch has a span of 174 feet and a maximum height of 30 feet. Find the height of the arch at 15 feet from its center.
A) 3.6 ft
B) 21.8 ft
C) 0.2 ft
D) 29.1 ft

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
A reflecting telescope has a mirror shaped like a paraboloid of revolution. If the distance of the vertex to the focus is 31 feet and the distance across the top of the mirror is 66 inches, how deep is the mirror in the center?
A reflecting telescope has a mirror shaped like a paraboloid of revolution. If the distance of the vertex to the focus is 31 feet and the distance across the top of the mirror is 66 inches, how deep is the mirror in the center?


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
59
Graph the equation.
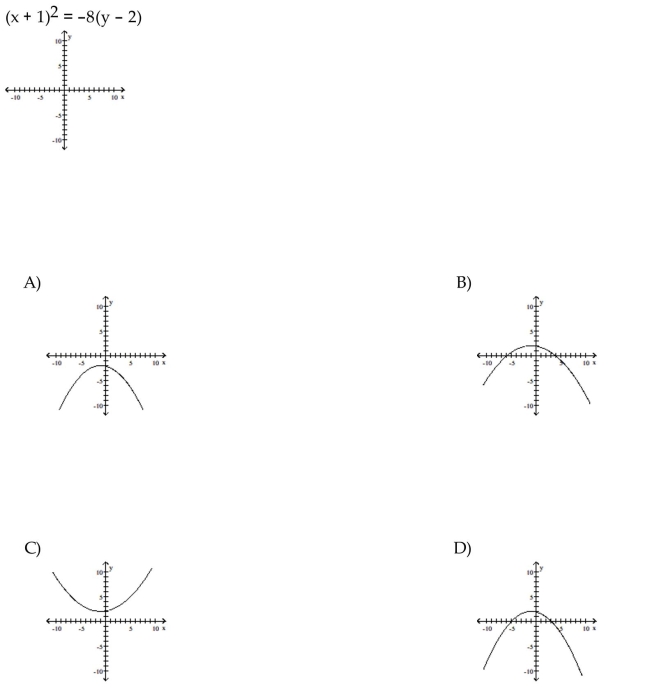


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. At some point along the road from the
Lowest point of the cable, the cable is 1.96 inches above the roadway. Find the distance between that point and
The base of the nearest tower.
A) 21 in.
B) 13.8 in.
C) 14.2 in.
D) 21.2 in.
An experimental model for a suspension bridge is built in the shape of a parabolic arch. In one section, cable runs from the top of one tower down to the roadway, just touching it there, and up again to the top of a second
Tower. The towers are both 12.25 inches tall and stand 70 inches apart. At some point along the road from the
Lowest point of the cable, the cable is 1.96 inches above the roadway. Find the distance between that point and
The base of the nearest tower.
A) 21 in.
B) 13.8 in.
C) 14.2 in.
D) 21.2 in.

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
61
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
62
Find an equation for the ellipse described.
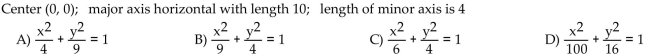
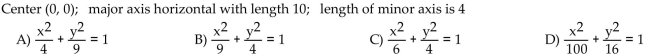

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
63
Graph the ellipse and locate the foci.
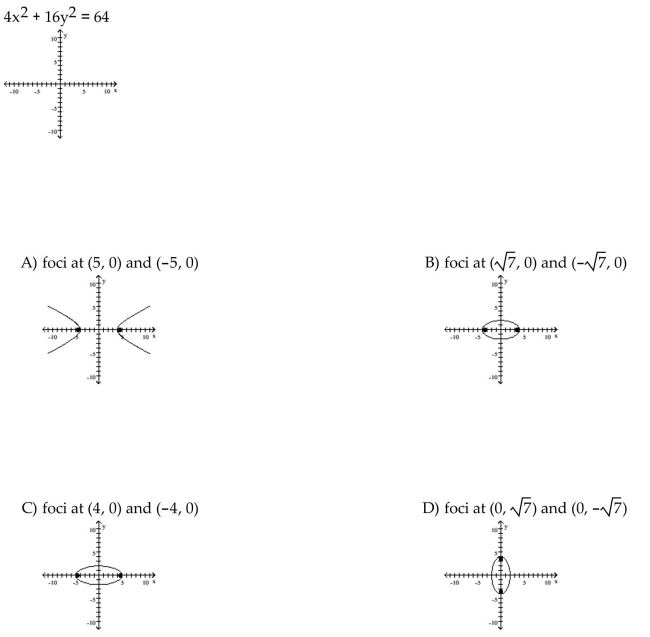


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
64
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
65
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
66
Find an equation for the ellipse described.
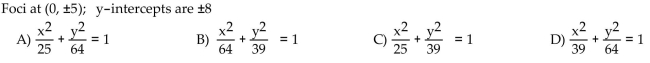
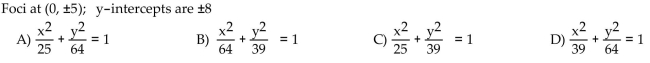

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
67
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
68
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
69
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
70
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
71
Graph the ellipse and locate the foci.
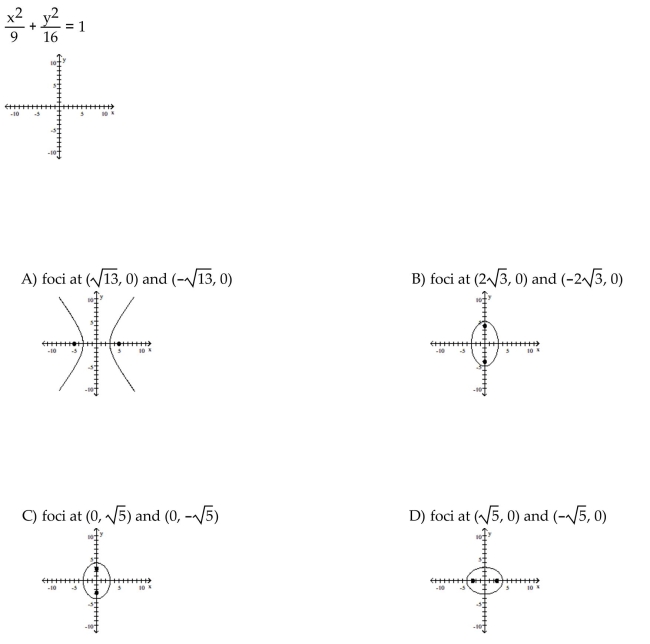


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
72
Write an equation for the graph.
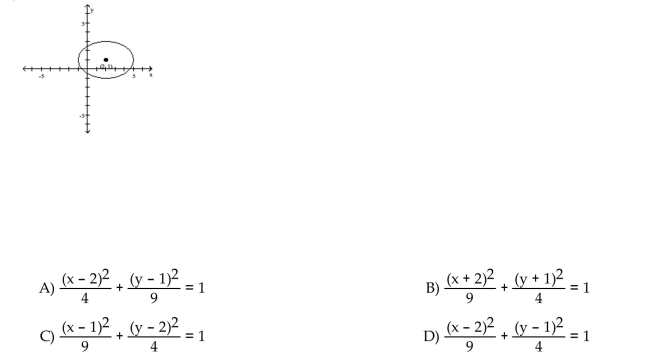
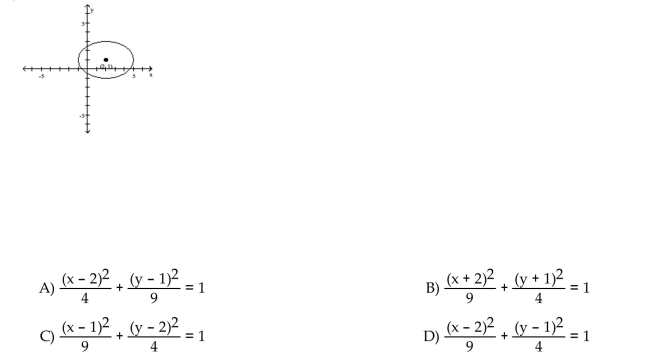

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
73
Graph the ellipse and locate the foci.
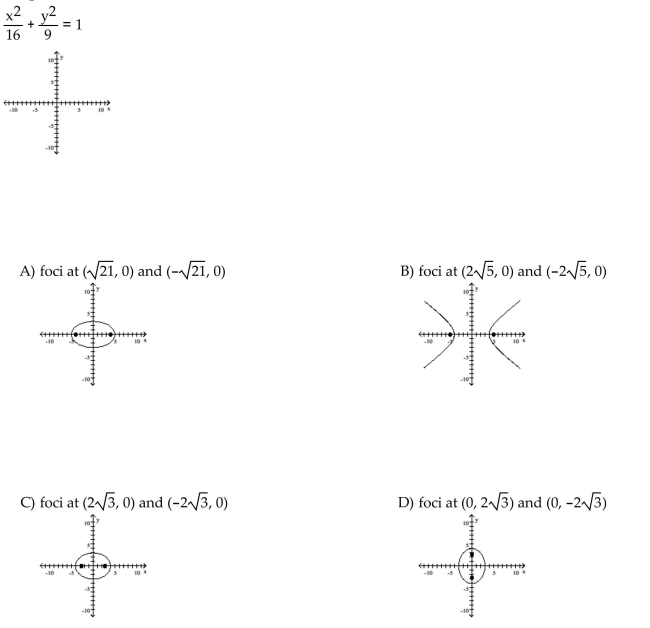


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
74
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
75
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
76
Graph the ellipse and locate the foci.
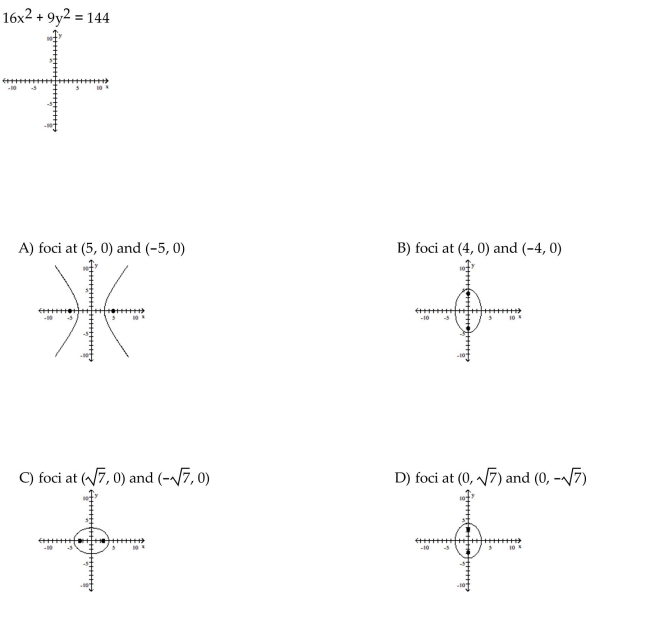


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
77
Graph the equation.
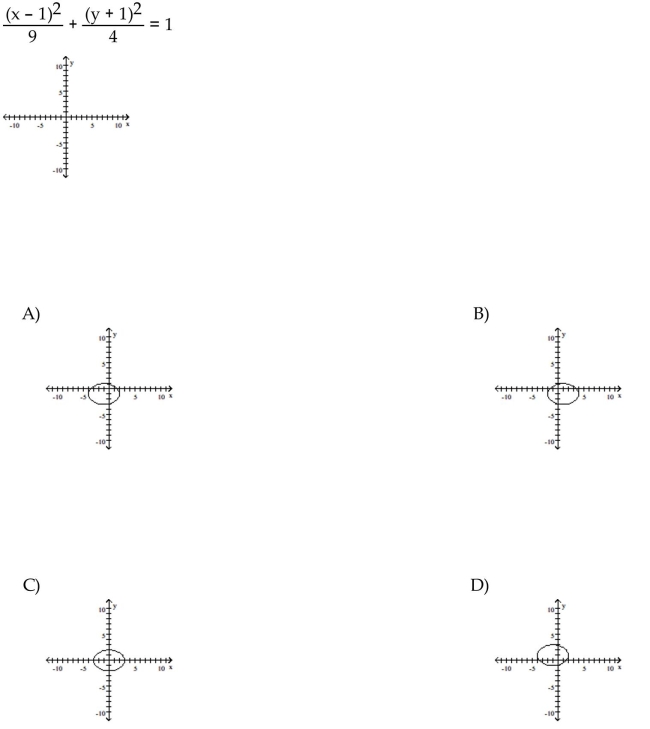


Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
78
Find the center, foci, and vertices of the ellipse.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
79
Find an equation for the ellipse described.



Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck
80
Find the center, foci, and vertices of the ellipse.
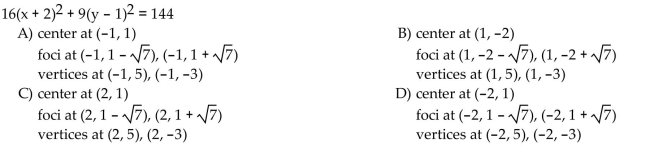
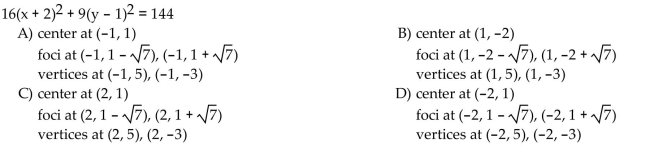

Unlock Deck
Unlock for access to all 197 flashcards in this deck.
Unlock Deck
k this deck


