Deck 9: Systems and Matrices
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/505
Play
Full screen (f)
Deck 9: Systems and Matrices
1
Solve the system by substitution.
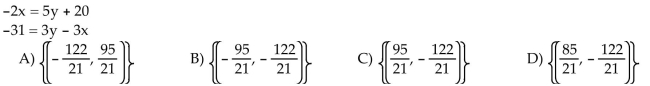
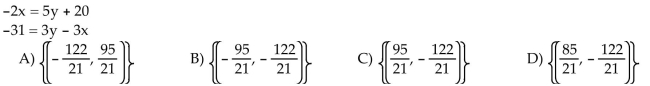
C
2
Solve the system by elimination.


C
3
Solve the system by substitution.


A
4
Solve the system by substitution.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
5
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 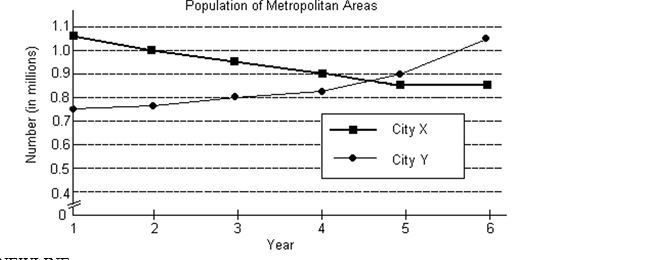
Express the solution of the system as an ordered pair.
A) approximately (3.9, 0.92)
B) approximately (1.2, 1.03)
C) approximately (4.6, 0.87)
D) approximately (3.1, 0.95)

Express the solution of the system as an ordered pair.
A) approximately (3.9, 0.92)
B) approximately (1.2, 1.03)
C) approximately (4.6, 0.87)
D) approximately (3.1, 0.95)

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the system by substitution.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system by substitution.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system by substitution.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
11
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 
If equations of the form y = f(t) were determined that modeled either of the two graphs, then the variable t would represent and the variable y would represent .
A) population (in millions); year
B) City Y; City X
C) City X; City Y
D) year; population (in millions)

If equations of the form y = f(t) were determined that modeled either of the two graphs, then the variable t would represent and the variable y would represent .
A) population (in millions); year
B) City Y; City X
C) City X; City Y
D) year; population (in millions)

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
13
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 
In what years was the population of the City X metropolitan area less than that of the City Y metropolitan area?
A) Years 1-5
B) Years 3-5
C) Years 5-6
D) Years 1-3

In what years was the population of the City X metropolitan area less than that of the City Y metropolitan area?
A) Years 1-5
B) Years 3-5
C) Years 5-6
D) Years 1-3

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system by elimination.
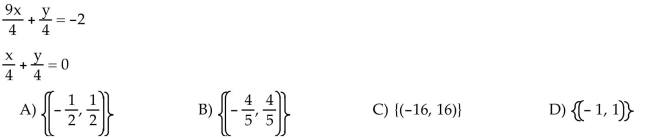
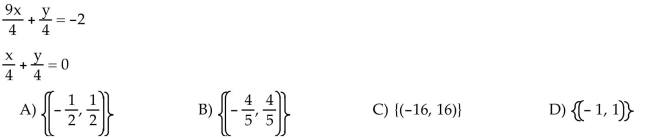

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the system by substitution.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
18
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 
Use the terms increasing, decreasing, and/or constant to describe the trends for the population of the City X metropolitan area.
A) The population of the City X metropolitan area was increasing from Year 1 to Year 6.
B) The population of the City X metropolitan area was decreasing from Year 1 to Year 5 and was constant from Year 5 to Year 6.
C) The population of the City X metropolitan area was decreasing from Year 1 to Year 6.
D) The population of the City X metropolitan area was increasing from Year 1 to Year 5 and was constant from Year 5 to Year 6.

Use the terms increasing, decreasing, and/or constant to describe the trends for the population of the City X metropolitan area.
A) The population of the City X metropolitan area was increasing from Year 1 to Year 6.
B) The population of the City X metropolitan area was decreasing from Year 1 to Year 5 and was constant from Year 5 to Year 6.
C) The population of the City X metropolitan area was decreasing from Year 1 to Year 6.
D) The population of the City X metropolitan area was increasing from Year 1 to Year 5 and was constant from Year 5 to Year 6.

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system by elimination.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
20
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 
At the time when the populations of the two metropolitan areas were equal, what was the approximate population of each area?
A) about 0.95 million
B) about 0.87 million
C) about 0.92 million
D) about 1.03 million

At the time when the populations of the two metropolitan areas were equal, what was the approximate population of each area?
A) about 0.95 million
B) about 0.87 million
C) about 0.92 million
D) about 1.03 million

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
21
Use a graphing calculator to solve the system. Express solutions with approximations to the nearest thousandth.
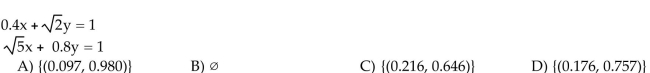
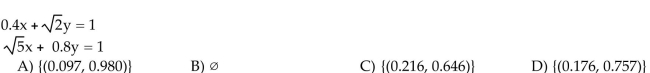

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
22
Use a graphing calculator to solve the system. Express solutions with approximations to the nearest thousandth.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
23
Use a graphing calculator to solve the system. Express solutions with approximations to the nearest thousandth.
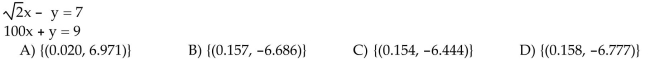
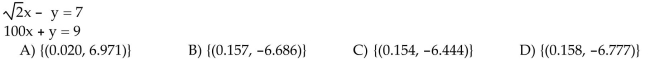

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.
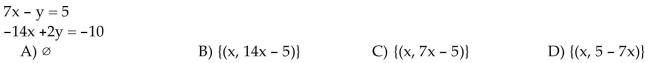
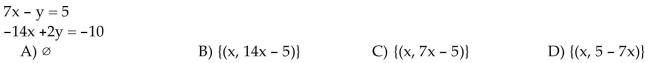

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the system.
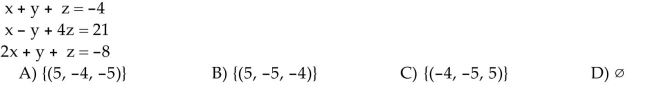
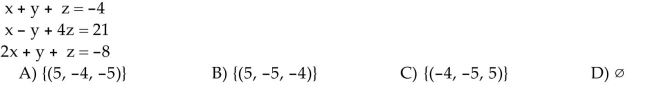

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
30
Use a graphing calculator to solve the system. Express solutions with approximations to the nearest thousandth.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
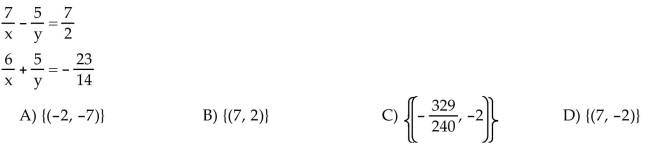
33
Solve the system.


Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.
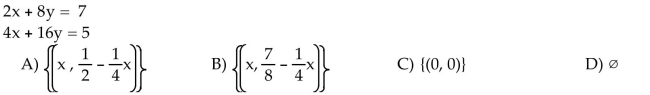
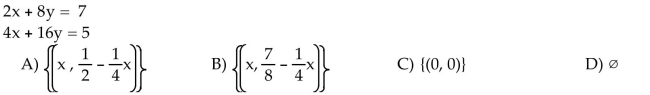

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
36
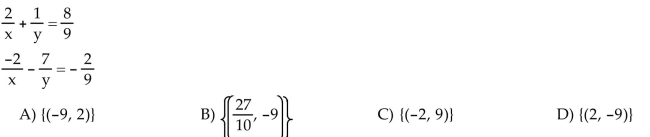
Solve the system.


Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
37
Use a graphing calculator to solve the system. Express solutions with approximations to the nearest thousandth.
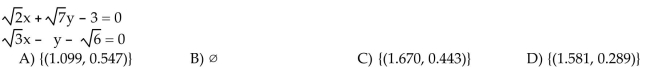
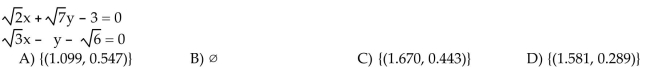

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the system by elimination.
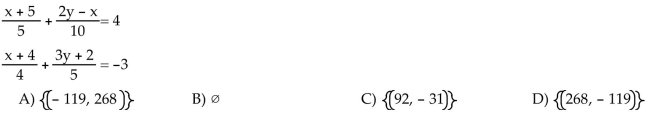
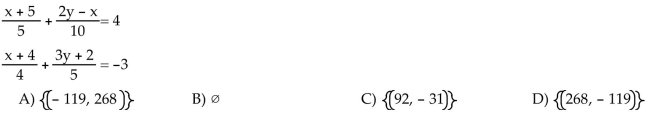

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.
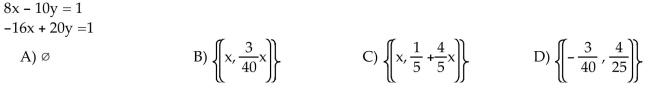
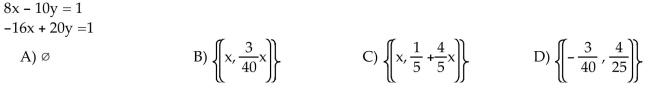

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the system.
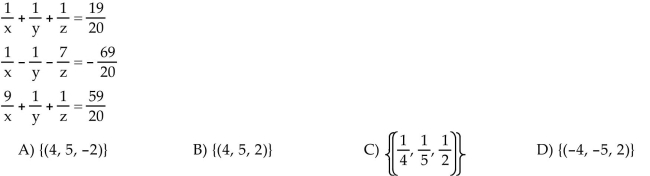
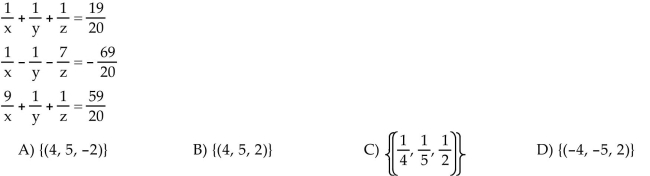

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
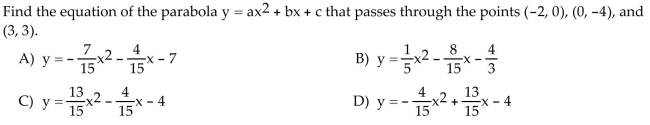
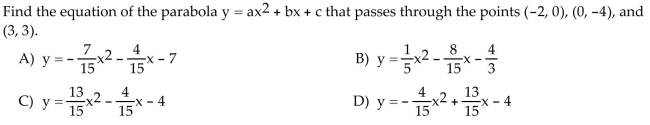

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the system in terms of the arbitrary variable x.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
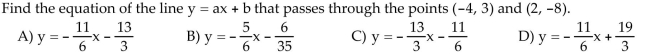
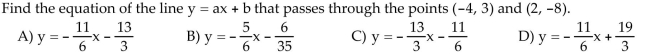

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the system.
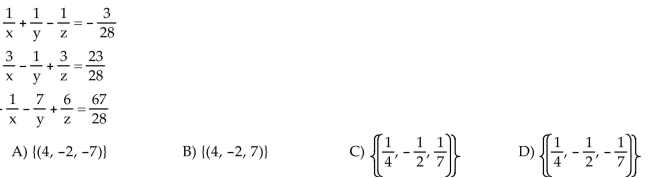


Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the system in terms of the arbitrary variable x.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the system.
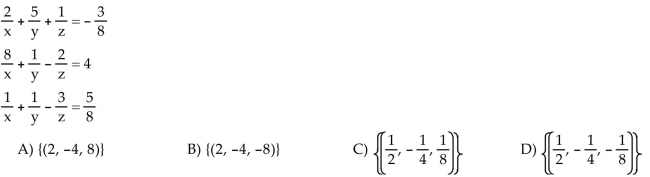
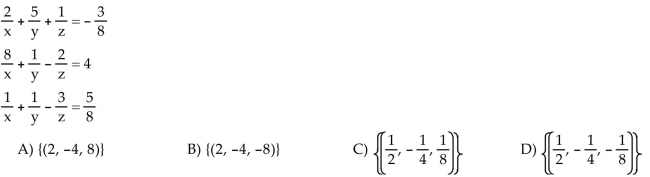

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the system.
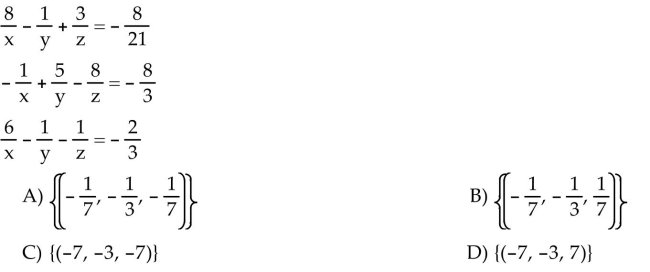
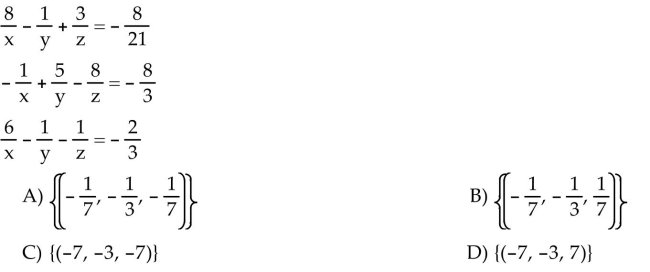

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the system.
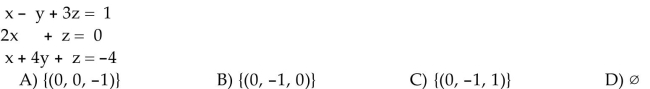
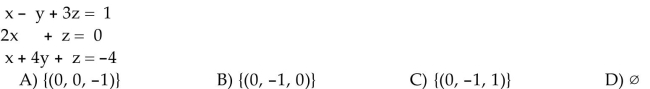

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the system.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the system.
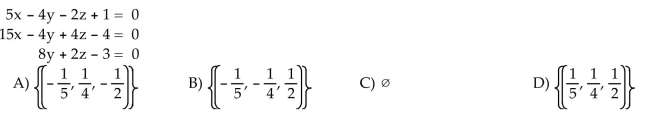
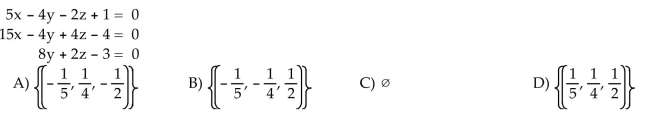

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. C requires 2 black, 1 white, and 2 red. The company used 95 black, 100
White and 80 red wires. How many of each type of cable were made?
A) 15 A; 16 B; 15 CB)15 A; 20 B; 15 CC)48A; 20 B; 12 CD)20 A; 15 B; 15 C
A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. C requires 2 black, 1 white, and 2 red. The company used 95 black, 100
White and 80 red wires. How many of each type of cable were made?
A) 15 A; 16 B; 15 CB)15 A; 20 B; 15 CC)48A; 20 B; 12 CD)20 A; 15 B; 15 C

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
A grain dealer sold to one customer 10 bushels of wheat, 8 of corn, and 5 of rye for $67.80; to another, 8 of wheat, 5 of corn, and 10 of rye for $67.90; and to a third, 5 of wheat, 10 of corn, and 8
Of rye for $69.00. What was the price per bushel for corn?
A) $3.30
B) $3.10
C) $2.80
D) $3.00
A grain dealer sold to one customer 10 bushels of wheat, 8 of corn, and 5 of rye for $67.80; to another, 8 of wheat, 5 of corn, and 10 of rye for $67.90; and to a third, 5 of wheat, 10 of corn, and 8
Of rye for $69.00. What was the price per bushel for corn?
A) $3.30
B) $3.10
C) $2.80
D) $3.00

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
A $64,000 trust is to be invested in bonds paying 6%, CDs paying 5%, and mortgages paying 10%. The bond and CD investment together must equal the mortgage investment. To earn a $4910
Annual income from the investments, how much should the bank invest in bonds?
A) $21,000
B) $32,000
C) $11,000
D) $9,000
A $64,000 trust is to be invested in bonds paying 6%, CDs paying 5%, and mortgages paying 10%. The bond and CD investment together must equal the mortgage investment. To earn a $4910
Annual income from the investments, how much should the bank invest in bonds?
A) $21,000
B) $32,000
C) $11,000
D) $9,000

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
A contractor mixes concrete from bags of pre-mix for small jobs. How many bags with 5% cement should he mix with 14 bags of 14.5% cement to produce a mix containing 12% cement?
A) 24 bags
B) 5 bags
C) 19 bags
D) 7 bags
A contractor mixes concrete from bags of pre-mix for small jobs. How many bags with 5% cement should he mix with 14 bags of 14.5% cement to produce a mix containing 12% cement?
A) 24 bags
B) 5 bags
C) 19 bags
D) 7 bags

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
Bob fenced in a rectangular garden in his yard. The length of the rectangle is 7 ft longer than the width and the perimeter is 66 ft. What is the width of the rectangle?
A) 15 ft
B) 26 ft
C) 13 ft
D) 12 ft
Bob fenced in a rectangular garden in his yard. The length of the rectangle is 7 ft longer than the width and the perimeter is 66 ft. What is the width of the rectangle?
A) 15 ft
B) 26 ft
C) 13 ft
D) 12 ft

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the problem.
The perimeter of a rectangle is 38 m. If the width were doubled and the length were increased by 10 m, the perimeter would be 70 m. What are the length and width of the rectangle?
A) Length: 9 m; width: 4 m
B) Length: 13 m; width: 6 m
C) Length: 6 m; width: 13 m
D) Length: 9 m; width: 9 m
The perimeter of a rectangle is 38 m. If the width were doubled and the length were increased by 10 m, the perimeter would be 70 m. What are the length and width of the rectangle?
A) Length: 9 m; width: 4 m
B) Length: 13 m; width: 6 m
C) Length: 6 m; width: 13 m
D) Length: 9 m; width: 9 m

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.
The sum of a studentʹs three scores is 218. If the first is 10 points more than the second, and the sum of the first two is 20 more than twice the third, what was the first score?
A) 56 points
B) 66 points
C) 81 points
D) 71 points
The sum of a studentʹs three scores is 218. If the first is 10 points more than the second, and the sum of the first two is 20 more than twice the third, what was the first score?
A) 56 points
B) 66 points
C) 81 points
D) 71 points

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the problem.
The perimeter of a triangle is 81 cm. The triangle is isosceles now, but if its base were lengthened by 4 cm and each leg were shortened by 5 cm, it would be equilateral. Find the length of the base
Of the original triangle.
A) 25 cm
B) 20 cm
C) 21 cm
D) 30 cm
The perimeter of a triangle is 81 cm. The triangle is isosceles now, but if its base were lengthened by 4 cm and each leg were shortened by 5 cm, it would be equilateral. Find the length of the base
Of the original triangle.
A) 25 cm
B) 20 cm
C) 21 cm
D) 30 cm

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged $90 for 3 days and 300 miles, while Mary was charged $162 for 5 days and 600 miles. What does Best Rental
Charge per day and per mile?
A) $17 per day; 13¢ per mile
B) $19 per day; 13¢ per mile
C) $12 per day; 18¢ per mile
D) $18 per day; 12¢ per mile
Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged $90 for 3 days and 300 miles, while Mary was charged $162 for 5 days and 600 miles. What does Best Rental
Charge per day and per mile?
A) $17 per day; 13¢ per mile
B) $19 per day; 13¢ per mile
C) $12 per day; 18¢ per mile
D) $18 per day; 12¢ per mile

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
Michaelʹs bank contains only nickels, dimes, and quarters. There are 65 coins in all, valued at $5.30. The number of nickels is 3 short of being three times the sum of the number of dimes and quarters.
How many dimes are in the bank?
A) 8 dimes
B) 9 dimes
C) 48 dimes
D) 14 dimes
Michaelʹs bank contains only nickels, dimes, and quarters. There are 65 coins in all, valued at $5.30. The number of nickels is 3 short of being three times the sum of the number of dimes and quarters.
How many dimes are in the bank?
A) 8 dimes
B) 9 dimes
C) 48 dimes
D) 14 dimes

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
Twice the water flow in the hot-water pipe is the same as three times the flow in the cold-water pipe. The combined flow is 1500 L/hr. What is the flow in each pipe?
A) 600 L/hr hot; 900 L/hr cold
B) 500 L/hr hot; 750 L/hr cold
C) 900 L/hr hot; 600 L/hr cold
D) 750 L/hr hot; 500 L/hr cold
Twice the water flow in the hot-water pipe is the same as three times the flow in the cold-water pipe. The combined flow is 1500 L/hr. What is the flow in each pipe?
A) 600 L/hr hot; 900 L/hr cold
B) 500 L/hr hot; 750 L/hr cold
C) 900 L/hr hot; 600 L/hr cold
D) 750 L/hr hot; 500 L/hr cold

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
The perimeter of a rectangle is 50 cm. The length is 11 cm longer than the width. What are the length and width of the rectangle?
A) Length: 11 cm; width: 7 cm
B) Length: 25 cm; width: 14 cm
C) Length: 18 cm; width: 7 cm
D) Length: 21 cm; width: 10 cm
The perimeter of a rectangle is 50 cm. The length is 11 cm longer than the width. What are the length and width of the rectangle?
A) Length: 11 cm; width: 7 cm
B) Length: 25 cm; width: 14 cm
C) Length: 18 cm; width: 7 cm
D) Length: 21 cm; width: 10 cm

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the problem.
Caroleʹs car averages 12.9 mi/gal in city driving and 21.8 mi/gal in highway driving. If she drove a total of 320.3 mi on 20 gal of gas, how many of the gallons were used for city driving?
A) 15 gal
B) 12 gal
C) 13 gal
D) 7 gal
Caroleʹs car averages 12.9 mi/gal in city driving and 21.8 mi/gal in highway driving. If she drove a total of 320.3 mi on 20 gal of gas, how many of the gallons were used for city driving?
A) 15 gal
B) 12 gal
C) 13 gal
D) 7 gal

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
Two different gasohol mixtures are available. One contains 5% alcohol and the other 12% alcohol. How much of each should be mixed to obtain 1000 gal of gasohol containing 10% alcohol?
A) 714 gal 5%; 714 gal 12%
B) 417 gal 5%; 583 gal 12%
C) 50 gal 5%; 120 gal 12%
D) 286 gal 5%; 714 gal 12%
Two different gasohol mixtures are available. One contains 5% alcohol and the other 12% alcohol. How much of each should be mixed to obtain 1000 gal of gasohol containing 10% alcohol?
A) 714 gal 5%; 714 gal 12%
B) 417 gal 5%; 583 gal 12%
C) 50 gal 5%; 120 gal 12%
D) 286 gal 5%; 714 gal 12%

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem.
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The combined income from the 5% and 6%
Investments is the same as the income from the 8% investment. Find the amount invested at each
Rate.
A) $8000 at 5%; $10,000 at 6%; $7000 at 8%
B) $10,000 at 5%; $5000 at 6%; $10,000 at 8%
C) $10,000 at 5%; $10,000 at 6%; $5000 at 8%
D) $5000 at 5%; $10,000 at 6%; $10,000 at 8%
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The combined income from the 5% and 6%
Investments is the same as the income from the 8% investment. Find the amount invested at each
Rate.
A) $8000 at 5%; $10,000 at 6%; $7000 at 8%
B) $10,000 at 5%; $5000 at 6%; $10,000 at 8%
C) $10,000 at 5%; $10,000 at 6%; $5000 at 8%
D) $5000 at 5%; $10,000 at 6%; $10,000 at 8%

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. C requires 2 black, 1 white, and 2 red. The company used 100 black, 110
White and 80 red wires. How many of each type of cable were made?
A) 20 A; 20 B; 83 CB)20 A; 93 B; 10 CC)10A; 20 B; 20 CD)20 A; 20 B; 10 C
A company makes 3 types of cable. Cable A requires 3 black, 3 white, and 2 red wires. B requires 1 black, 2 white, and 1 red. C requires 2 black, 1 white, and 2 red. The company used 100 black, 110
White and 80 red wires. How many of each type of cable were made?
A) 20 A; 20 B; 83 CB)20 A; 93 B; 10 CC)10A; 20 B; 20 CD)20 A; 20 B; 10 C

Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem.



Unlock Deck
Unlock for access to all 505 flashcards in this deck.
Unlock Deck
k this deck


