Deck 5: Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/158
Play
Full screen (f)
Deck 5: Probability Distributions
1
Provide an appropriate response.
Sampling without replacement involves dependent events, so this would not be considered a binomial experiment. Explain the circumstances under which sampling without replacement could be considered independent and, thus, binomial.
Sampling without replacement involves dependent events, so this would not be considered a binomial experiment. Explain the circumstances under which sampling without replacement could be considered independent and, thus, binomial.
When the sample size is no more than 5% of the total population size.
2
Provide an appropriate response.
-Describe the differences in the Poisson and the binomial distribution.
-Describe the differences in the Poisson and the binomial distribution.
The Poisson computes probabilities for occurrences of events over some interval.
The Poisson distribution is affected only by the mean µ, whereas the binomial is affected by sample size n and probability p.
The Poisson distribution has discrete values from 1, 2, 3, . . . with no upper limit. A binomial distribution has discrete values from 1, 2, 3, to n; that is, the upper limit of values is n.
The Poisson distribution is affected only by the mean µ, whereas the binomial is affected by sample size n and probability p.
The Poisson distribution has discrete values from 1, 2, 3, . . . with no upper limit. A binomial distribution has discrete values from 1, 2, 3, to n; that is, the upper limit of values is n.
3
Provide an appropriate response.
-Identify each of the variables in the Binomial Probability Formula.
Also, explain what the fraction computes.
-Identify each of the variables in the Binomial Probability Formula.
Also, explain what the fraction computes.
n is the fixed number of trials, x is the number of successes, p is the probability of success in one of the n trials, and q is the probability of failure in one of the n trials. The fraction determines the number of different orders of x successes out of n trials.
4
Identify the given random variable
-The number of freshmen in the required course, English 101
A)Discrete
B)Continuous
-The number of freshmen in the required course, English 101
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
5
Provide an appropriate response.
Describe the Poisson distribution and give an example of a random variable with a Poisson distribution.
Describe the Poisson distribution and give an example of a random variable with a Poisson distribution.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
6
Provide an appropriate response.
-Suppose an event has a 80% chance of success. Show a probability distribution for the number of successes in 8 trials. Find the mean and SD. Create an interval of ±2 SD about the mean. Would exactly 4 successes out of 8 be an unusual occurrence? Justify your answer in terms of the Range Rule of Thumb.
-Suppose an event has a 80% chance of success. Show a probability distribution for the number of successes in 8 trials. Find the mean and SD. Create an interval of ±2 SD about the mean. Would exactly 4 successes out of 8 be an unusual occurrence? Justify your answer in terms of the Range Rule of Thumb.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
7
Identify the given random variable
-The number of oil spills occurring off the Alaskan coast
A)Discrete
B)Continuous
-The number of oil spills occurring off the Alaskan coast
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
8
Provide an appropriate response.
A game is said to be "fair" if the expected value for winnings is 0, that is, in the long run, the player can expect to win 0. Consider the following game. The game costs $1 to play and the winnings are $5 for red, $3 for blue, $2 for yellow, and nothing for white. The following probabilities apply. What are your expected winnings? Does the game favor the player or the owner?
A game is said to be "fair" if the expected value for winnings is 0, that is, in the long run, the player can expect to win 0. Consider the following game. The game costs $1 to play and the winnings are $5 for red, $3 for blue, $2 for yellow, and nothing for white. The following probabilities apply. What are your expected winnings? Does the game favor the player or the owner?


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
List the four requirements for a binomial distribution. Describe an experiment which is binomial and discuss how the experiment fits each of the four requirements.
List the four requirements for a binomial distribution. Describe an experiment which is binomial and discuss how the experiment fits each of the four requirements.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
10
Provide an appropriate response.
List the four requirements of a Poisson distribution.
List the four requirements of a Poisson distribution.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
11
Provide an appropriate response.
Previously we learned to find the three important characteristics of data: the measure of central tendency, the measure of variation, and the nature of the distribution, We can find the same three characteristics for a binomial distribution. Given a binomial distribution with p = 0.4 and n = 8, find the three characteristics.
Previously we learned to find the three important characteristics of data: the measure of central tendency, the measure of variation, and the nature of the distribution, We can find the same three characteristics for a binomial distribution. Given a binomial distribution with p = 0.4 and n = 8, find the three characteristics.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
12
Provide an appropriate response.
Compare the probability histogram for the expected sum with the actual results. What do you conclude about the dice results displayed in the Actual Sum of Two Dice histogram?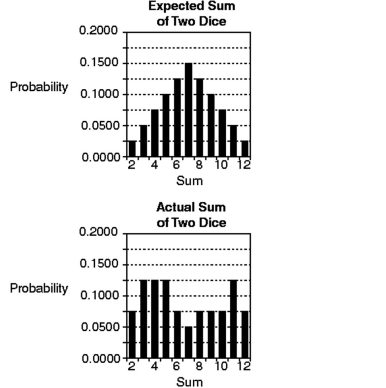
Compare the probability histogram for the expected sum with the actual results. What do you conclude about the dice results displayed in the Actual Sum of Two Dice histogram?


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
13
Provide an appropriate response.
-Suppose a mathematician computed the expected value of winnings for a person playing each of seven different games in a casino. What would you expect to be true for all expected values for these seven games?
-Suppose a mathematician computed the expected value of winnings for a person playing each of seven different games in a casino. What would you expect to be true for all expected values for these seven games?

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
14
Identify the given random variable
-The pH level in a shampoo
A)Discrete
B)Continuous
-The pH level in a shampoo
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
15
Identify the given random variable
-The number of phone calls between New York and California on Thanksgiving day
A)Discrete
B)Continuous
-The number of phone calls between New York and California on Thanksgiving day
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
16
Provide an appropriate response.
Do probability distributions measure what did happen or what will probably happen? How do we use probability distributions to make decisions?
Do probability distributions measure what did happen or what will probably happen? How do we use probability distributions to make decisions?

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
17
Identify the given random variable
-The cost of a randomly selected orange
A)Discrete
B)Continuous
-The cost of a randomly selected orange
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
18
Identify the given random variable
-The height of a randomly selected student
A)Discrete
B)Continuous
-The height of a randomly selected student
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
19
Provide an appropriate response.
-List the two requirements for a probability histogram. Discuss the relationship between the sum of the probabilities in a probability distribution and the total area represented by the bars in a probability histogram.
-List the two requirements for a probability histogram. Discuss the relationship between the sum of the probabilities in a probability distribution and the total area represented by the bars in a probability histogram.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
20
Provide an appropriate response.
List the three methods for finding binomial probabilities in the table below, and then complete the table to discuss the advantages and disadvantages of each.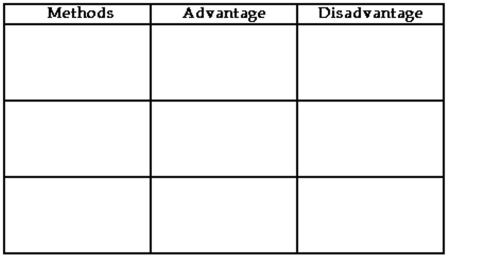
List the three methods for finding binomial probabilities in the table below, and then complete the table to discuss the advantages and disadvantages of each.


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
21
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.
In a certain town, 70% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree.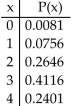
In a certain town, 70% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree.


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
22
Find the mean of the given probability distribution.
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.5470, 0.3562, 0.0870, 0.0094, and 0.0004, respectively. Round answer to the nearest hundredth.
A)2.00
B)0.56
C)1.11
D)0.46
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.5470, 0.3562, 0.0870, 0.0094, and 0.0004, respectively. Round answer to the nearest hundredth.
A)2.00
B)0.56
C)1.11
D)0.46

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
23
Identify the given random variable
-The braking time of a car
A)Discrete
B)Continuous
-The braking time of a car
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.
-In a certain town, 40% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree. Find the standard deviation for the probability distribution.
A)0.96
B)1.12
C)1.88
D)0.98
-In a certain town, 40% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree. Find the standard deviation for the probability distribution.
A)0.96
B)1.12
C)1.88
D)0.98

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.
If a person is randomly selected from a certain town, the probability distribution for the number, x, of siblings is as described in the accompanying table.
If a person is randomly selected from a certain town, the probability distribution for the number, x, of siblings is as described in the accompanying table.


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
26
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.



Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
27
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.
A police department reports that the probabilities that 0, 1, 2, 3, and 4 car thefts will be reported in a given day are 0.202, 0.323, 0.258, 0.138, and 0.055, respectively.
A police department reports that the probabilities that 0, 1, 2, 3, and 4 car thefts will be reported in a given day are 0.202, 0.323, 0.258, 0.138, and 0.055, respectively.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the problem.
-Find the standard deviation for the given probability distribution.
A)2.45
B)2.56
C)1.60
D)1.71
-Find the standard deviation for the given probability distribution.
A)2.45
B)2.56
C)1.60
D)1.71

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
29
Find the mean of the given probability distribution.
A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.50, 0.38, 0.11, and 0.01, respectively.
A)0.63
B)0.25
C)1.50
D)1.13
A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.50, 0.38, 0.11, and 0.01, respectively.
A)0.63
B)0.25
C)1.50
D)1.13

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
30
Find the mean of the given probability distribution.
-The number of golf balls ordered by customers of a pro shop has the following probability distribution.
A)8.22
B)9
C)6.63
D)9.3
-The number of golf balls ordered by customers of a pro shop has the following probability distribution.
A)8.22
B)9
C)6.63
D)9.3

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
31
Find the mean of the given probability distribution.
-
A) 1.45
B)1.64
C)1.55
D)1.74
-
A) 1.45
B)1.64
C)1.55
D)1.74

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
32
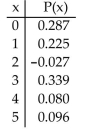
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.


Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
33
Determine whether the following is a probability distribution. If not, identify the requirement that is not satisfied.



Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
34
Find the mean of the given probability distribution.
-The accompanying table shows the probability distribution for x, the number that shows up when a loaded die is rolled.
A)0.17
B)3.50
C)3.85
D)3.98
-The accompanying table shows the probability distribution for x, the number that shows up when a loaded die is rolled.
A)0.17
B)3.50
C)3.85
D)3.98

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the problem.
-Find the variance for the given probability distribution.
A)2.63
B)7.43
C)2.69
D)2.46
-Find the variance for the given probability distribution.
A)2.63
B)7.43
C)2.69
D)2.46

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
36
Find the mean of the given probability distribution.
-In a certain town, 30% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree.
A)1.10
B)2.00
C)1.44
D)1.20
-In a certain town, 30% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree.
A)1.10
B)2.00
C)1.44
D)1.20

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
37
Find the mean of the given probability distribution.
-The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate office. Its probability distribution is as follows.
A)3.60
B)3.40
C)3.50
D)3.35
-The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate office. Its probability distribution is as follows.
A)3.60
B)3.40
C)3.50
D)3.35

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
38
Identify the given random variable
-The number of field goals kicked in a football game
A)Discrete
B)Continuous
-The number of field goals kicked in a football game
A)Discrete
B)Continuous

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
-Find the variance for the given probability distribution.
A)1.56
B)2.44
C)2.85
D)1.69
-Find the variance for the given probability distribution.
A)1.56
B)2.44
C)2.85
D)1.69

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
-The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate Office. Its probability distribution is as follows. Find the standard deviation for the probability distribution.
A)6.86
B)4.45
C)2.62
D)2.25
-The random variable x is the number of houses sold by a realtor in a single month at the Sendsom's Real Estate Office. Its probability distribution is as follows. Find the standard deviation for the probability distribution.
A)6.86
B)4.45
C)2.62
D)2.25

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
Suppose you pay $3.00 to roll a fair die with the understanding that you will get back $5.00 for rolling a 3 or a 6, nothing otherwise. What is your expected value?
A)$3.00
B)-$1.33
C)-$3.00
D)$5.00
Suppose you pay $3.00 to roll a fair die with the understanding that you will get back $5.00 for rolling a 3 or a 6, nothing otherwise. What is your expected value?
A)$3.00
B)-$1.33
C)-$3.00
D)$5.00

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
42
Use the normal distribution to approximate the desired probability.
Find the probability of selecting 12 or more girls.
A)0.001
B)0.007
C)0.006
D)0.022
Find the probability of selecting 12 or more girls.
A)0.001
B)0.007
C)0.006
D)0.022

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.4521, 0.3970, 0.1307, 0.0191, and 0.0010, respectively. Find the variance for the probability distribution.
A)0.59
B)0.77
C)1.11
D)0.51
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.4521, 0.3970, 0.1307, 0.0191, and 0.0010, respectively. Find the variance for the probability distribution.
A)0.59
B)0.77
C)1.11
D)0.51

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
A contractor is considering a sale that promises a profit of $23,000 with a probability of 0.7 or a loss (due to bad weather, strikes, and such)of $13,000 with a probability of 0.3. What is the expected profit?
A)$12,200
B)$25,200
C)$16,100
D)$10,000
A contractor is considering a sale that promises a profit of $23,000 with a probability of 0.7 or a loss (due to bad weather, strikes, and such)of $13,000 with a probability of 0.3. What is the expected profit?
A)$12,200
B)$25,200
C)$16,100
D)$10,000

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
45
Assume that there is a 0.15 probability that a basketball playoff series will last four games, a 0.30 probability that it will last five games, a 0.25 probability that it will last six games, and a 0.30 probability that it will last seven games. Is it unusual for a team to win a series in 5 games?
A)Yes
B)No
A)Yes
B)No

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
A 28-year-old man pays $57 for a one-year life insurance policy with coverage of $100,000. If the probability that he will live through the year is 0.9992, what is the expected value for the insurance policy?
A)-$56.95
B)$99,920.00
C)$23.00
D)$80.00
A 28-year-old man pays $57 for a one-year life insurance policy with coverage of $100,000. If the probability that he will live through the year is 0.9992, what is the expected value for the insurance policy?
A)-$56.95
B)$99,920.00
C)$23.00
D)$80.00

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.6274, 0.3102, 0.0575, 0.0047, and 0.0001, respectively. Find the standard deviation for the probability distribution.
A)0.39
B)0.63
C)0.76
D)0.56
The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.6274, 0.3102, 0.0575, 0.0047, and 0.0001, respectively. Find the standard deviation for the probability distribution.
A)0.39
B)0.63
C)0.76
D)0.56

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
In a game, you have a 1/42 probability of winning $67 and a 41/42 probability of losing $7. What is your expected value?
A)$1.60
B)$8.43
C)-$5.24
D)-$6.83
In a game, you have a 1/42 probability of winning $67 and a 41/42 probability of losing $7. What is your expected value?
A)$1.60
B)$8.43
C)-$5.24
D)-$6.83

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
49
Use the normal distribution to approximate the desired probability.
The prizes that can be won in a sweepstakes are listed below together with the chances of winning each one: $5300 (1 chance in 8600); $2500 (1 chance in 5300); $700 (1 chance in 3500); $200 (1 chance in 2800). Find the expected value of the amount won for one entry if the cost of entering is 73 cents.
A)$0.67
B)$0.63
C)$1.29
D)$200
The prizes that can be won in a sweepstakes are listed below together with the chances of winning each one: $5300 (1 chance in 8600); $2500 (1 chance in 5300); $700 (1 chance in 3500); $200 (1 chance in 2800). Find the expected value of the amount won for one entry if the cost of entering is 73 cents.
A)$0.67
B)$0.63
C)$1.29
D)$200

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
Suppose you buy 1 ticket for $1 out of a lottery of 1,000 tickets where the prize for the one winning ticket is to be $500. What is your expected value?
A)-$0.40
B)-$0.50
C)-$1.00
D)$0.00
Suppose you buy 1 ticket for $1 out of a lottery of 1,000 tickets where the prize for the one winning ticket is to be $500. What is your expected value?
A)-$0.40
B)-$0.50
C)-$1.00
D)$0.00

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
51
Use the normal distribution to approximate the desired probability.
Find the probability of selecting exactly 5 girls.
A)0.022
B)0.122
C)0.001
D)0.061
Find the probability of selecting exactly 5 girls.
A)0.022
B)0.122
C)0.001
D)0.061

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
52
Focus groups of 10 people are randomly selected to discuss products of the Famous Company. It is determined that the mean number (per group)who recognize the Famous brand name is 4.8, and the standard deviation is 0.73. Would it be unusual to randomly select 10 people and find that greater than 8 recognize the Famous brand name?
A)No
B)Yes
A)No
B)Yes

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
53
Use the normal distribution to approximate the desired probability.
Find the probability of selecting exactly 8 girls.
A)0.183
B)0.000
C)0.022
D)0.122
Find the probability of selecting exactly 8 girls.
A)0.183
B)0.000
C)0.022
D)0.122

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the problem.
-In a certain town, 60% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree. Find the variance for the probability distribution.
A)6.72
B)0.98
C)0.84
D)0.96
-In a certain town, 60% of adults have a college degree. The accompanying table describes the probability distribution for the number of adults (among 4 randomly selected adults)who have a college degree. Find the variance for the probability distribution.
A)6.72
B)0.98
C)0.84
D)0.96

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
55
Use the normal distribution to approximate the desired probability.
Find the probability of selecting exactly 4 girls.
A)0.022
B)0.061
C)0.122
D)0.001
Find the probability of selecting exactly 4 girls.
A)0.022
B)0.061
C)0.122
D)0.001

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
-The accompanying table shows the probability distribution for x, the number that shows up when a loaded die is rolled. Find the variance for the probability distribution.
A)12.86
B)9.62
C)2.36
D)2.03
-The accompanying table shows the probability distribution for x, the number that shows up when a loaded die is rolled. Find the variance for the probability distribution.
A)12.86
B)9.62
C)2.36
D)2.03

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
57
Assume that a researcher randomly selects 14 newborn babies and counts the number of girls selected, x. The probabilities
corresponding to the 14 possible values of x are summarized in the given table. Answer the question using the table.
-Find the probability of selecting 2 or more girls.
A)0.994
B)0.006
C)0.999
D)0.001
corresponding to the 14 possible values of x are summarized in the given table. Answer the question using the table.
-Find the probability of selecting 2 or more girls.
A)0.994
B)0.006
C)0.999
D)0.001

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
58
Use the normal distribution to approximate the desired probability.
Find the probability of selecting 9 or more girls.
A)0.061
B)0.001
C)0.122
D)0.212
Find the probability of selecting 9 or more girls.
A)0.061
B)0.001
C)0.122
D)0.212

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
59
Focus groups of 12 people are randomly selected to discuss products of the Yummy Company. It is determined that the mean number (per group)who recognize the Yummy brand name is 9.4, and the standard deviation is 0.98. Would it be unusual to randomly select 12 people and find that fewer than 5 recognize the Yummy brand name?
A)No
B)Yes
A)No
B)Yes

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.52, 0.40, 0.07, and 0.01, respectively. Find the standard deviation for the probability distribution. Round answer to the nearest hundredth.
A)0.98
B)0.88
C)0.45
D)0.67
A police department reports that the probabilities that 0, 1, 2, and 3 burglaries will be reported in a given day are 0.52, 0.40, 0.07, and 0.01, respectively. Find the standard deviation for the probability distribution. Round answer to the nearest hundredth.
A)0.98
B)0.88
C)0.45
D)0.67

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
61
Assume that there is a 0.05 probability that a sports playoff series will last four games, a 0.45 probability that it will last five games, a 0.45 probability that it will last six games, and a 0.05 probability that it will last seven games. Is it unusual for a team to win a series in 7 games?
A)No
B)Yes
A)No
B)Yes

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
62
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Spinning a roulette wheel 3 times, keeping track of the winning numbers.
A)Not binomial: the trials are not independent.
B)Procedure results in a binomial distribution.
C)Not binomial: there are too many trials.
D)Not binomial: there are more than two outcomes for each trial.
-Spinning a roulette wheel 3 times, keeping track of the winning numbers.
A)Not binomial: the trials are not independent.
B)Procedure results in a binomial distribution.
C)Not binomial: there are too many trials.
D)Not binomial: there are more than two outcomes for each trial.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
63
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Rolling a single die 19 times, keeping track of the numbers that are rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Not binomial: the trials are not independent.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution.
-Rolling a single die 19 times, keeping track of the numbers that are rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Not binomial: the trials are not independent.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
64
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Rolling a single die 46 times, keeping track of the "fives" rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Procedure results in a binomial distribution.
C)Not binomial: there are too many trials.
D)Not binomial: the trials are not independent.
-Rolling a single die 46 times, keeping track of the "fives" rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Procedure results in a binomial distribution.
C)Not binomial: there are too many trials.
D)Not binomial: the trials are not independent.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
65
Answer the question.
-Suppose that a law enforcement group studying traffic violations determines that the accompanying table describes the probability distribution for five randomly selected people, where x is the number that have received a speeding ticket in the last 2 years. Is it unusual to find no speeders among five randomly selected people?
A)Yes
B)No
-Suppose that a law enforcement group studying traffic violations determines that the accompanying table describes the probability distribution for five randomly selected people, where x is the number that have received a speeding ticket in the last 2 years. Is it unusual to find no speeders among five randomly selected people?
A)Yes
B)No

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
66
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Spinning a roulette wheel 7 times, keeping track of the occurrences of a winning number of "16".
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution..
-Spinning a roulette wheel 7 times, keeping track of the occurrences of a winning number of "16".
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution..

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
67
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
- n = 10, x = 2, p =
A)0.1951
B)0.1929
C)0.2156
D)0.0028
- n = 10, x = 2, p =
A)0.1951
B)0.1929
C)0.2156
D)0.0028

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
68
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Choosing 10 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time with replacement, keeping track of the colors of the marbles chosen.
A)Procedure results in a binomial distribution.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: the trials are not independent.
D)Not binomial: there are too many trials.
-Choosing 10 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time with replacement, keeping track of the colors of the marbles chosen.
A)Procedure results in a binomial distribution.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: the trials are not independent.
D)Not binomial: there are too many trials.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
69
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
- n = 6, x = 3,
A)0.0536
B)0.0154
C)0.0322
D)0.0286
- n = 6, x = 3,
A)0.0536
B)0.0154
C)0.0322
D)0.0286

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
70
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Rolling a single "loaded" die 48 times, keeping track of the "fives" rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Not binomial: there are too many trials.
C)Procedure results in a binomial distribution.
D)Not binomial: the trials are not independent.
-Rolling a single "loaded" die 48 times, keeping track of the "fives" rolled.
A)Not binomial: there are more than two outcomes for each trial.
B)Not binomial: there are too many trials.
C)Procedure results in a binomial distribution.
D)Not binomial: the trials are not independent.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
71
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Rolling a single "loaded" die 58 times, keeping track of the numbers that are rolled.
A)Procedure results in a binomial distribution.
B)Not binomial: there are too many trials.
C)Not binomial: the trials are not independent.
D)Not binomial: there are more than two outcomes for each trial.
-Rolling a single "loaded" die 58 times, keeping track of the numbers that are rolled.
A)Procedure results in a binomial distribution.
B)Not binomial: there are too many trials.
C)Not binomial: the trials are not independent.
D)Not binomial: there are more than two outcomes for each trial.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
72
Suppose that voting in municipal elections is being studied and that the accompanying tables describes the probability distribution for four randomly selected people, where x is the number that voted in the last election. Is it unusual to find four voters among four randomly selected people?
A)Yes
B)No
A)Yes
B)No

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose that computer literacy among people ages 40 and older is being studied and that the accompanying tables describes the probability distribution for four randomly selected people, where x is the number that are computer literate. Is it unusual to find four computer literates among four randomly selected people?
A)Yes
B)No
A)Yes
B)No

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
74
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
n = 5, x = 2, p = 0.70
A)0.700
B)0.198
C)0.132
D)0.464
n = 5, x = 2, p = 0.70
A)0.700
B)0.198
C)0.132
D)0.464

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
75
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Choosing 5 people (without replacement)from a group of 59 people, of which 15 are women, keeping track of the number of men chosen.
A)Not binomial: there are too many trials.
B)Not binomial: there are more than two outcomes for each trial.
C)Procedure results in a binomial distribution.
D)Not binomial: the trials are not independent.
-Choosing 5 people (without replacement)from a group of 59 people, of which 15 are women, keeping track of the number of men chosen.
A)Not binomial: there are too many trials.
B)Not binomial: there are more than two outcomes for each trial.
C)Procedure results in a binomial distribution.
D)Not binomial: the trials are not independent.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
76
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
77
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Choosing 3 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time with replacement, keeping track of the number of red marbles chosen.
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution.
-Choosing 3 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time with replacement, keeping track of the number of red marbles chosen.
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Not binomial: there are too many trials.
D)Procedure results in a binomial distribution.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose that weight of adolescents is being studied by a health organization and that the accompanying tables describes the probability distribution for three randomly selected adolescents, where x is the number who are considered morbidly obese. Is it unusual to have no obese subjects among three randomly selected adolescents?
A)No
B)Yes
A)No
B)Yes

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
79
Determine whether the given procedure results in a binomial distribution. If not, state the reason why.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck
80
Determine whether the given procedure results in a binomial distribution. If not, state the reason why
-Choosing 8 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time without replacement, keeping track of the number of red marbles chosen.
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Procedure results in a binomial distribution.
D)Not binomial: there are too many trials.
-Choosing 8 marbles from a box of 40 marbles (20 purple, 12 red, and 8 green)one at a time without replacement, keeping track of the number of red marbles chosen.
A)Not binomial: the trials are not independent.
B)Not binomial: there are more than two outcomes for each trial.
C)Procedure results in a binomial distribution.
D)Not binomial: there are too many trials.

Unlock Deck
Unlock for access to all 158 flashcards in this deck.
Unlock Deck
k this deck


