Deck 4: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/171
Play
Full screen (f)
Deck 4: Probability
1
Provide an appropriate response.
Discuss why the relative frequency method of computing probabilities might be chosen over the classical method.
Discuss why the relative frequency method of computing probabilities might be chosen over the classical method.
Possible answers include the possibility that the experiment is so complicated that determining the
sample space for the classical is too difficult, or the ability to more quickly and easily conduct the
experiment by a simulation on a computer.
sample space for the classical is too difficult, or the ability to more quickly and easily conduct the
experiment by a simulation on a computer.
2
Provide an appropriate response.
Compare the relative frequency formula for finding probabilities to the classical formula for finding probabilities. How are the two formulas similar and how are they different? What special requirements does the classical approach have?
Compare the relative frequency formula for finding probabilities to the classical formula for finding probabilities. How are the two formulas similar and how are they different? What special requirements does the classical approach have?
In the relative frequency formula, the probabilities are determined by conducting an experiment,
counting the number of occurrences of the event, and creating the ratio of number of occurrences to
number of times the experiment was conducted. In the classical approach, a sample space of all of the
possible simple events is created and the number of successes is compared to the number of different
simple events. In the classical approach, each outcome must be equally likely.
counting the number of occurrences of the event, and creating the ratio of number of occurrences to
number of times the experiment was conducted. In the classical approach, a sample space of all of the
possible simple events is created and the number of successes is compared to the number of different
simple events. In the classical approach, each outcome must be equally likely.
3
Provide an appropriate response.
-If a game were "fair," the payoff on a bet would be the same as the odds for the event. In one game, the odds for winning are 1:13. If the game were "fair," what would the payoff be for a $5 bet? Of course, games in casinos are designed to make a profit for the casino investors. Supposing the casino makes the payoff at 1:11 odds, what profit does the casino make on your winning bet?
-If a game were "fair," the payoff on a bet would be the same as the odds for the event. In one game, the odds for winning are 1:13. If the game were "fair," what would the payoff be for a $5 bet? Of course, games in casinos are designed to make a profit for the casino investors. Supposing the casino makes the payoff at 1:11 odds, what profit does the casino make on your winning bet?
In a "fair" game the payoff would be $70 = 13·5 + 5 original bet. The casino payoff would be $60 = 11·5 + 5original bet. The profit would be $10.
4
Provide an appropriate response.
-List two reasons it is better to sample without replacement when testing batches of products. When sampling without replacement, should you use the multiplication rule for independent or dependent events? Explain your answer.
-List two reasons it is better to sample without replacement when testing batches of products. When sampling without replacement, should you use the multiplication rule for independent or dependent events? Explain your answer.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
5
Provide an appropriate response.
Compare probabilities and odds. How can you convert odds to probabilities?
Compare probabilities and odds. How can you convert odds to probabilities?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
6
Provide an appropriate response.
Under what circumstances can you sample without replacement and still use the multiplication rule for independence? Discuss population and sample size as you answer this question.
Under what circumstances can you sample without replacement and still use the multiplication rule for independence? Discuss population and sample size as you answer this question.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
7
Provide an appropriate response.
Probabilities are useful in the decision-making process. Suppose a random sample of 152 students was surveyed regarding an instructor's teaching. Suppose 105 students rated the instructor either excellent or above average on lecture presentations, 96 students rated the instructor as giving difficult or very difficult assignments and tests. Would you take this instructor for a class? Discuss the influence of probabilities on making this decision.
Probabilities are useful in the decision-making process. Suppose a random sample of 152 students was surveyed regarding an instructor's teaching. Suppose 105 students rated the instructor either excellent or above average on lecture presentations, 96 students rated the instructor as giving difficult or very difficult assignments and tests. Would you take this instructor for a class? Discuss the influence of probabilities on making this decision.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
8
Provide an appropriate response.
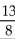 On an exam on probability concepts, Sue had an answer of for one problem. Explain how she knew that this result was incorrect.
On an exam on probability concepts, Sue had an answer of for one problem. Explain how she knew that this result was incorrect.
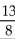 On an exam on probability concepts, Sue had an answer of for one problem. Explain how she knew that this result was incorrect.
On an exam on probability concepts, Sue had an answer of for one problem. Explain how she knew that this result was incorrect.
Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
9
Provide an appropriate response.
-What important question must you answer before computing an "and" probability? How does the answer influence your computation?
-What important question must you answer before computing an "and" probability? How does the answer influence your computation?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
10
Provide an appropriate response.
-Discuss the differences, both in applications and in the formulas, for combinations and permutations. Give an example of each.
-Discuss the differences, both in applications and in the formulas, for combinations and permutations. Give an example of each.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
11
Provide an appropriate response.
Sometimes probabilities derived by the relative frequency method differ from the probabilities expected from classical probability methods. How does the law of large numbers apply in this situation?
Sometimes probabilities derived by the relative frequency method differ from the probabilities expected from classical probability methods. How does the law of large numbers apply in this situation?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
12
Provide an appropriate response.
Describe an event whose probability of occurring is 1 and explain what that probability means. Describe an event whose probability of occurring is 0 and explain what that probability means.
Describe an event whose probability of occurring is 1 and explain what that probability means. Describe an event whose probability of occurring is 0 and explain what that probability means.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
13
Provide an appropriate response.
Discuss the advantages and disadvantages of odds.
Discuss the advantages and disadvantages of odds.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
14
Provide an appropriate response.
Discuss the range of possible values for probabilities. Give examples to support each.
Discuss the range of possible values for probabilities. Give examples to support each.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
15
Provide an appropriate response.
-Describe the process for making a tree diagram and give an example.
-Describe the process for making a tree diagram and give an example.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
16
Provide an appropriate response.
-Interpret the symbol P(B|A)and explain what is meant by the expression. What do we know if P(B|A)is not the same as P(B)?
-Interpret the symbol P(B|A)and explain what is meant by the expression. What do we know if P(B|A)is not the same as P(B)?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
17
Provide an appropriate response.
-Define mutually exclusive events and independent events. Give an example of each.
-Define mutually exclusive events and independent events. Give an example of each.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
18
Provide an appropriate response.
-Give an example of events which are independent but not mutually exclusive.
-Give an example of events which are independent but not mutually exclusive.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
19
Provide an appropriate response.
-What important question must you answer before computing an "or" probability? How does the answer influence your computation?
-What important question must you answer before computing an "or" probability? How does the answer influence your computation?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
20
Provide an appropriate response.
When asked about the probability that he would become a sumo wrestler, Sam replied "slim to none." Relate that phrase to a numeric probability and interpret his meaning.
When asked about the probability that he would become a sumo wrestler, Sam replied "slim to none." Relate that phrase to a numeric probability and interpret his meaning.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
21
Express the indicated degree of likelihood as a probability value.
"You have a 50-50 chance of choosing the correct answer."
A)0.9
B)0.25
C)50
D)0.50
"You have a 50-50 chance of choosing the correct answer."
A)0.9
B)0.25
C)50
D)0.50

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
22
Express the indicated degree of likelihood as a probability value.
-"You cannot determine the exact decimal-number value of
A)0
B)0.5
C)3.14
D)1
-"You cannot determine the exact decimal-number value of
A)0
B)0.5
C)3.14
D)1

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
23
Find the indicated probability
-If a person is randomly selected, find the probability that his or her birthday is in May. Ignore leap years.
A)
B)
C)
D)
-If a person is randomly selected, find the probability that his or her birthday is in May. Ignore leap years.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
24
Answer the question.
-Which of the following cannot be a probability?
A)
B)
C)
D)
-Which of the following cannot be a probability?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
25
Express the indicated degree of likelihood as a probability value.
"There is a 40% chance of rain tomorrow."
A)4
B)0.60
C)40
D)0.40
"There is a 40% chance of rain tomorrow."
A)4
B)0.60
C)40
D)0.40

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
26
Find the indicated probability
-A die with 12 sides is rolled. What is the probability of rolling a number less than 11?
A) 10
B)
C)
D)
-A die with 12 sides is rolled. What is the probability of rolling a number less than 11?
A) 10
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
27
Provide an appropriate response.
Suppose a student is taking a 5-response multiple choice exam; that is, the choices are A, B, C, D, and E, with only one of the responses correct. Describe the complement method for determining the probability of getting at least one of the questions correct on the 15-question exam. Why would the complement method be the method of choice for this problem?
Suppose a student is taking a 5-response multiple choice exam; that is, the choices are A, B, C, D, and E, with only one of the responses correct. Describe the complement method for determining the probability of getting at least one of the questions correct on the 15-question exam. Why would the complement method be the method of choice for this problem?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
28
Find the indicated probability
-A sample space consists of 13 separate events that are equally likely. What is the probability of each?
A)1
B)0
C)13
D)
-A sample space consists of 13 separate events that are equally likely. What is the probability of each?
A)1
B)0
C)13
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
29
Answer the question.
-What is the probability of an event that is certain to occur?
A)0.95
B)1
C)0.5
D)0.99
-What is the probability of an event that is certain to occur?
A)0.95
B)1
C)0.5
D)0.99

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
30
Express the indicated degree of likelihood as a probability value.
"Your mother could not have died two years before you were born."
A)0.25
B)0.5
C)1
D)0
"Your mother could not have died two years before you were born."
A)0.25
B)0.5
C)1
D)0

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
31
Find the indicated probability
-Two 6-sided dice are rolled. What is the probability that the sum of the two numbers on the dice will be 5?
A)
B)
C)
D) 4
-Two 6-sided dice are rolled. What is the probability that the sum of the two numbers on the dice will be 5?
A)
B)
C)
D) 4

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
32
Answer the question.
-What is the probability of an impossible event?
A)-1
B)1
C)0
D)0.1
-What is the probability of an impossible event?
A)-1
B)1
C)0
D)0.1

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
33
Answer the question.
-On a multiple choice test with four possible answers for each question, what is the probability of answering a question correctly if you make a random guess?
A) 1
B)
C)
D)
-On a multiple choice test with four possible answers for each question, what is the probability of answering a question correctly if you make a random guess?
A) 1
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
34
Express the indicated degree of likelihood as a probability value.
"It will definitely turn dark tonight."
A)0.67
B)0.5
C)1
D)0.30
"It will definitely turn dark tonight."
A)0.67
B)0.5
C)1
D)0.30

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
35
Answer the question.
-Which of the following cannot be a probability?
A)
B)-1
C)0
D)1
-Which of the following cannot be a probability?
A)
B)-1
C)0
D)1

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
36
Find the indicated probability
-On a multiple choice test, each question has 7 possible answers. If you make a random guess on the first question, what is the probability that you are correct?
A) 0
B)
C) 7
D) 1
-On a multiple choice test, each question has 7 possible answers. If you make a random guess on the first question, what is the probability that you are correct?
A) 0
B)
C) 7
D) 1

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
37
Provide an appropriate response.
-Consider the following formulas: and
Given the same values for and in each formula, which is the smaller value, or ? How does this relate to th concept of counting the number of outcomes based on whether or not order is a criterion?
-Consider the following formulas: and
Given the same values for and in each formula, which is the smaller value, or ? How does this relate to th concept of counting the number of outcomes based on whether or not order is a criterion?

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
38
Find the indicated probability
-A bag contains 2 red marbles, 3 blue marbles, and 5 green marbles. If a marble is randomly selected from the bag, what is the probability that it is blue?
A)
B)
C)
D)
-A bag contains 2 red marbles, 3 blue marbles, and 5 green marbles. If a marble is randomly selected from the bag, what is the probability that it is blue?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
39
Find the indicated probability
-A class consists of 46 women and 81 men. If a student is randomly selected, what is the probability that the student is a woman?
A)
B)
C)
D)
-A class consists of 46 women and 81 men. If a student is randomly selected, what is the probability that the student is a woman?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
40
Use the Poisson Distribution to find the indicated probability.
"You have one chance in ten of winning the race."
A)0.10
B)0.5
C)0.90
D)1
"You have one chance in ten of winning the race."
A)0.10
B)0.5
C)0.90
D)1

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
41
Estimate the probability of the event.
In a certain class of students, there are 12 boys from Wilmette, 3 girls from Winnetka, 8 girls from Wilmette, 4 boys from Glencoe, 3 boys from Winnetka and 9 girls from Glenoce. If the teacher calls upon a student to answer a question, what is the probability that the student will be a boy?
A)0.308
B)0.487
C)0.767
D)0.41
In a certain class of students, there are 12 boys from Wilmette, 3 girls from Winnetka, 8 girls from Wilmette, 4 boys from Glencoe, 3 boys from Winnetka and 9 girls from Glenoce. If the teacher calls upon a student to answer a question, what is the probability that the student will be a boy?
A)0.308
B)0.487
C)0.767
D)0.41

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
42
Find the indicated probability.
If a person told you in what month he was born, would it be "unusual" to guess the date of his birth (not including the year)?
A)Yes
B)No
If a person told you in what month he was born, would it be "unusual" to guess the date of his birth (not including the year)?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
43
Estimate the probability of the event
-In a certain class of students, there are 9 boys from Wilmette, 5 girls from Kenilworth, 7 girls from Wilmette, 6 boys from Glencoe, 5 boys from Kenilworth and 3 girls from Glenoce. If the teacher calls upon a student to answer a question, what is the probability that the student will be from Kenilworth?
A)0.25
B)0.37
C)0.286
D)0.143
-In a certain class of students, there are 9 boys from Wilmette, 5 girls from Kenilworth, 7 girls from Wilmette, 6 boys from Glencoe, 5 boys from Kenilworth and 3 girls from Glenoce. If the teacher calls upon a student to answer a question, what is the probability that the student will be from Kenilworth?
A)0.25
B)0.37
C)0.286
D)0.143

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
44
Answer the question, considering an event to be "unusual" if its probability is less than or equal to 0.05.
Assume that one student in your class of 31 students is randomly selected to win a prize. Would it be "unusual" for you to win?
A)No
B)Yes
Assume that one student in your class of 31 students is randomly selected to win a prize. Would it be "unusual" for you to win?
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
45
Estimate the probability of the event
-Of 1338 people who came into a blood bank to give blood, 253 people had high blood pressure. Estimate the probability that the next person who comes in to give blood will have high blood pressure.
A)0.157
B)0.189
C)0.24
D)0.108
-Of 1338 people who came into a blood bank to give blood, 253 people had high blood pressure. Estimate the probability that the next person who comes in to give blood will have high blood pressure.
A)0.157
B)0.189
C)0.24
D)0.108

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
46
Friskie is having her fifth litter. The prior litters have either been three normal pups or two normal pups and a runt. Assume the probability of either outcome is 50%.
A)NNR NNN
B)N NN NR NNN NRN
C)NNN RNN NR
D)NR NNR NNR
A)NNR NNN
B)N NN NR NNN NRN
C)NNN RNN NR
D)NR NNR NNR

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
47
Both Fred and Ed have a bag of candy containing a lemon drop, a cherry drop, and a lollipop. Each takes out a piece and eats it. What are the possible pairs of candies eaten?
A) LD-LD CD-LD LP-LP LD-LP CD-CD LD-LP LP-CD CD-LD LP-LD
B) LD-LD CD-LD LP-LP LD-CD CD-CD LD-LP LP-CD CD-LP LP-LD
C) LD-CD LD-CD LD-CD LD-LP LD-LP LD-LP CD-LP CD-LP CD-LP
D) CD-LD LD-LP LP-CD LP-LP LD-LD
A) LD-LD CD-LD LP-LP LD-LP CD-CD LD-LP LP-CD CD-LD LP-LD
B) LD-LD CD-LD LP-LP LD-CD CD-CD LD-LP LP-CD CD-LP LP-LD
C) LD-CD LD-CD LD-CD LD-LP LD-LP LD-LP CD-LP CD-LP CD-LP
D) CD-LD LD-LP LP-CD LP-LP LD-LD

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
48
From the information provided, create the sample space of possible outcomes
-Flip a coin twice.
A)HT TH
B)HH TT HT HT
C)HH HT TH TT
D)HH HT TT
-Flip a coin twice.
A)HT TH
B)HH TT HT HT
C)HH HT TH TT
D)HH HT TT

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
49
Find the indicated probability.
Is it "unusual" to get a 12 when a pair of dice is rolled?
A)No
B)Yes
Is it "unusual" to get a 12 when a pair of dice is rolled?
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
50
Find the indicated probability.
If you drew one card from a standard deck, would it be "unusual" to draw an ace of hearts?
A)Yes
B)No
If you drew one card from a standard deck, would it be "unusual" to draw an ace of hearts?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
51
Find the indicated probability.
Assume that a study of 500 randomly selected school bus routes showed that 486 arrived on time. Is it "unusual" for a school bus to arrive late?
A)No
B)Yes
Assume that a study of 500 randomly selected school bus routes showed that 486 arrived on time. Is it "unusual" for a school bus to arrive late?
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
52
Find the indicated probability.
If you are told that a mystery person's name begins with a consonant, would it be "unusual" to guess the first letter of that person's name?
A)Yes
B)No
If you are told that a mystery person's name begins with a consonant, would it be "unusual" to guess the first letter of that person's name?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
53
Find the indicated probability.
Is it "unusual" to get 9 when a pair of dice is rolled?
A)Yes
B)No
Is it "unusual" to get 9 when a pair of dice is rolled?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
54
Estimate the probability of the event
-A polling firm, hired to estimate the likelihood of the passage of an up-coming referendum, obtained the set of survey responses to make its estimate. The encoding system for the data is: 0 = FOR, 1 = AGAINST. If the referendum were held today, estimate the probability that it would pass. 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0
A)0.65
B)0.6
C)0.4
D)0.5
-A polling firm, hired to estimate the likelihood of the passage of an up-coming referendum, obtained the set of survey responses to make its estimate. The encoding system for the data is: 0 = FOR, 1 = AGAINST. If the referendum were held today, estimate the probability that it would pass. 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0
A)0.65
B)0.6
C)0.4
D)0.5

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
55
Find the indicated probability.
If you drew one card from a standard deck, would it be "unusual" to draw a 7?
A)Yes
B)No
If you drew one card from a standard deck, would it be "unusual" to draw a 7?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
56
Find the indicated probability.
A multiple choice question has 16 possible answers, only one of which is correct. Is it "unusual" to answer a question correctly if a random guess is made?
A)No
B)Yes
A multiple choice question has 16 possible answers, only one of which is correct. Is it "unusual" to answer a question correctly if a random guess is made?
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
57
From the information provided, create the sample space of possible outcomes
-Flip a coin three times.
A) HH? ?TT ?TH TTT HTT THH H?T THT
B) H?? ??? ??? ??? ?H? THT TTH TTT
C) HH? TTT THT HTH HHT TTH HTH
D) HTT THT HTH HHH TTH TTT
-Flip a coin three times.
A) HH? ?TT ?TH TTT HTT THH H?T THT
B) H?? ??? ??? ??? ?H? THT TTH TTT
C) HH? TTT THT HTH HHT TTH HTH
D) HTT THT HTH HHH TTH TTT

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
58
Find the indicated probability
-In a poll, respondents were asked whether they had ever been in a car accident. 196 respondents indicated that they had been in a car accident and 118 respondents said that they had not been in a car accident. If one of these respondents is randomly selected, what is the probability of getting someone who has been in a car accident? Round to the nearest thousandth, if necessary.
A)0.376
B)0.624
C)0.005
D)1.661
-In a poll, respondents were asked whether they had ever been in a car accident. 196 respondents indicated that they had been in a car accident and 118 respondents said that they had not been in a car accident. If one of these respondents is randomly selected, what is the probability of getting someone who has been in a car accident? Round to the nearest thousandth, if necessary.
A)0.376
B)0.624
C)0.005
D)1.661

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
59
Estimate the probability of the event
-The data set represents the income levels of the members of a country club. Estimate the probability that a randomly selected member earns at least $90,000. Round your answers to the nearest tenth.
A)0.4
B)0.7
C)0.8
D)0.6
-The data set represents the income levels of the members of a country club. Estimate the probability that a randomly selected member earns at least $90,000. Round your answers to the nearest tenth.
A)0.4
B)0.7
C)0.8
D)0.6

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
60
Find the indicated probability.
Assume that a study of 300 randomly selected school bus routes showed that 272 arrived on time. Is it "unusual" for a school bus to arrive late?
A)Yes
B)No
Assume that a study of 300 randomly selected school bus routes showed that 272 arrived on time. Is it "unusual" for a school bus to arrive late?
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
61
Determine whether the events are mutually exclusive
-Meet a man with an umbrella. Meet a man with a raincoat.
A)Yes
B)No
-Meet a man with an umbrella. Meet a man with a raincoat.
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
62
Determine whether the events are mutually exclusive.
-A spinner has equal regions numbered 1 through 15. What is the probability that the spinner will stop on an even number or a multiple of 3?
A)
B) 12
C)
D)
-A spinner has equal regions numbered 1 through 15. What is the probability that the spinner will stop on an even number or a multiple of 3?
A)
B) 12
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
63
Answer the question.
Suppose you are playing a game of chance. If you bet $7 on a certain event, you will collect $280 (including your $7 bet)if you win. Find the odds used for determining the payoff.
A)40 : 1
B)1 : 39
C)39 : 1
D)280 : 287
Suppose you are playing a game of chance. If you bet $7 on a certain event, you will collect $280 (including your $7 bet)if you win. Find the odds used for determining the payoff.
A)40 : 1
B)1 : 39
C)39 : 1
D)280 : 287

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
64
From the information provided, create the sample space of possible outcomes
-Two white mice mate. The male has both a white and a black fur-color gene. The female has only white fur-color genes. The fur color of the offspring depends on the pairs of fur-color genes that they receive. Assume that neither the white nor the black gene dominates. List the possible outcomes. W = white and B = black
A)WW, BB
B)WB, BW
C)WW, WW
D)WW, BW
-Two white mice mate. The male has both a white and a black fur-color gene. The female has only white fur-color genes. The fur color of the offspring depends on the pairs of fur-color genes that they receive. Assume that neither the white nor the black gene dominates. List the possible outcomes. W = white and B = black
A)WW, BB
B)WB, BW
C)WW, WW
D)WW, BW

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
65
Determine whether the events are mutually exclusive
-Draw one ball colored red from a bag. Draw one ball colored blue from the same bag.
A)No
B)Yes
-Draw one ball colored red from a bag. Draw one ball colored blue from the same bag.
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
66
Answer the question
-Find the odds against correctly guessing the answer to a multiple choice question with 4 possible answers.
A)4 : 1
B)3 : 1
C)3 : 4
D)4 : 3
-Find the odds against correctly guessing the answer to a multiple choice question with 4 possible answers.
A)4 : 1
B)3 : 1
C)3 : 4
D)4 : 3

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
67
Determine whether the events are mutually exclusive.
A sample of 100 wood and 100 graphite tennis rackets are taken from the warehouse. If 5 wood and 10 graphite are defective and one racket is randomly selected from the sample, find the probability that the racket is wood or defective.
A)0.525
B)0.075
C)0.55
D)There is insufficient information to answer the question.
A sample of 100 wood and 100 graphite tennis rackets are taken from the warehouse. If 5 wood and 10 graphite are defective and one racket is randomly selected from the sample, find the probability that the racket is wood or defective.
A)0.525
B)0.075
C)0.55
D)There is insufficient information to answer the question.

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
68
Determine whether the events are mutually exclusive.
-Find , given that .
A) 0
B)
C)
D)
-Find , given that .
A) 0
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
69
Determine whether the events are mutually exclusive.
-If you pick a card at random from a well shuffled deck, what is the probability that you get a face card or a spade?
A)
B)
C)
D)
-If you pick a card at random from a well shuffled deck, what is the probability that you get a face card or a spade?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
70
Determine whether the events are mutually exclusive
-Get a full time day job as a teller with a bank. Get a full time day job as a cashier at a store.
A)No
B)Yes
-Get a full time day job as a teller with a bank. Get a full time day job as a cashier at a store.
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
71
Determine whether the events are mutually exclusive.
Based on meteorological records, the probability that it will snow in a certain town on January 1st is 0.206. Find the probability that in a given year it will not snow on January 1st in that town.
A)0.794
B)4.854
C)0.259
D)1.206
Based on meteorological records, the probability that it will snow in a certain town on January 1st is 0.206. Find the probability that in a given year it will not snow on January 1st in that town.
A)0.794
B)4.854
C)0.259
D)1.206

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
72
Determine whether the events are mutually exclusive.
-If a person is randomly selected, find the probability that his or her birthday is not in May. Ignore leap years.
A)
B)
C)
D)
-If a person is randomly selected, find the probability that his or her birthday is not in May. Ignore leap years.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
73
Determine whether the events are mutually exclusive
-Get stung by a bee. Get stung by a wasp.
A)No
B)Yes
-Get stung by a bee. Get stung by a wasp.
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
74
Answer the question
-In a certain town, 10% of people commute to work by bicycle. If a person is selected randomly from the town, what are the odds against selecting someone who commutes by bicycle?
A)1 : 9
B)9 : 1
C)9 : 10
D)1 : 10
-In a certain town, 10% of people commute to work by bicycle. If a person is selected randomly from the town, what are the odds against selecting someone who commutes by bicycle?
A)1 : 9
B)9 : 1
C)9 : 10
D)1 : 10

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
75
Determine whether the events are mutually exclusive
-Find a ten dollar bill on the sidewalk. Find a ten dollar bill on the grass.
A)No
B)Yes
-Find a ten dollar bill on the sidewalk. Find a ten dollar bill on the grass.
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
76
Determine whether the events are mutually exclusive.
The probability that Luis will pass his statistics test is 0.42. Find the probability that he will fail his statistics test.
A)2.38
B)0.72
C)0.21
D)0.58
The probability that Luis will pass his statistics test is 0.42. Find the probability that he will fail his statistics test.
A)2.38
B)0.72
C)0.21
D)0.58

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
77
Determine whether the events are mutually exclusive.
-The table below describes the smoking habits of a group of asthma sufferers. If one of the 1073 people is randomly selected, find the probability that the person is a man or a heavy smoker.
A)0.545
B)0.580
C)0.614
D)0.487
-The table below describes the smoking habits of a group of asthma sufferers. If one of the 1073 people is randomly selected, find the probability that the person is a man or a heavy smoker.
A)0.545
B)0.580
C)0.614
D)0.487

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
78
Determine whether the events are mutually exclusive
-Go to a formal dinner affair. Wear blue jeans.
A)Yes
B)No
-Go to a formal dinner affair. Wear blue jeans.
A)Yes
B)No

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
79
Determine whether the events are mutually exclusive
-Read a book by Mark Twain. Read about Tom Sawyer.
A)No
B)Yes
-Read a book by Mark Twain. Read about Tom Sawyer.
A)No
B)Yes

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck
80
Determine whether the events are mutually exclusive.
-If , find .
A)
B) 0
C)
D)
-If , find .
A)
B) 0
C)
D)

Unlock Deck
Unlock for access to all 171 flashcards in this deck.
Unlock Deck
k this deck


