Deck 4: Polynomial and Rational Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/94
Play
Full screen (f)
Deck 4: Polynomial and Rational Functions
1
Use the leading-term test to match the function with the correct graph.
A)
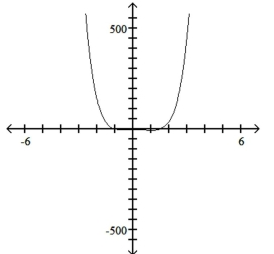
B)
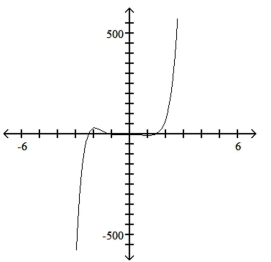
C)
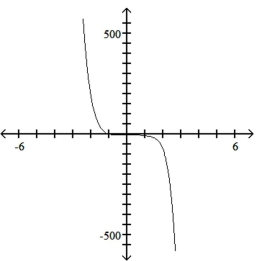
D)
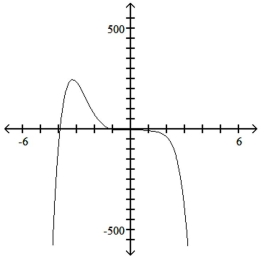
A)

B)

C)

D)

D
2
Use the leading-term test to match the function with the correct graph.
A)
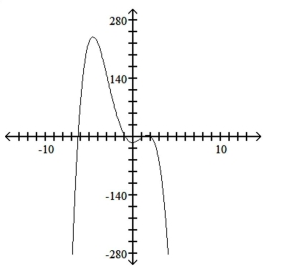
B)
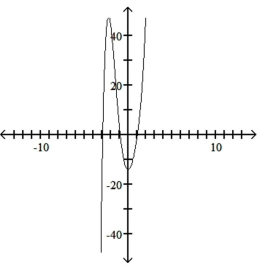
C)
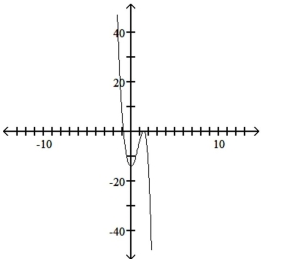
D)
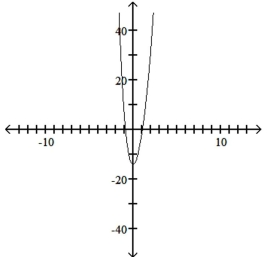
A)

B)

C)

D)

D
3
Find the zeros of the polynomial function and state the multiplicity of each.
A) , multiplicity , multiplicity , multiplicity 1
B) , multiplicity , multiplicity 1
C) , multiplicity , multiplicity , multiplicity 1
D) , multiplicity , multiplicity 2
A) , multiplicity , multiplicity , multiplicity 1
B) , multiplicity , multiplicity 1
C) , multiplicity , multiplicity , multiplicity 1
D) , multiplicity , multiplicity 2
C
4
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
5
Use the leading-term test to match the function with the correct graph.
A)
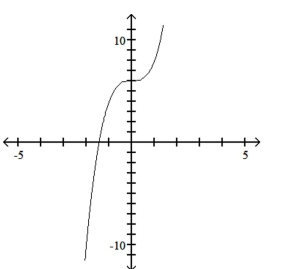
B)
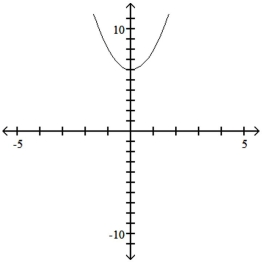
C)
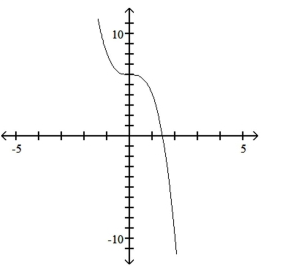
D)
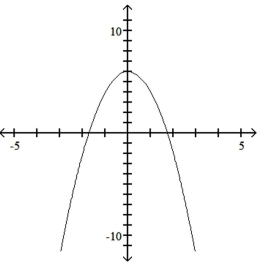
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
6
Match the equation with the appropriate graph.
A)
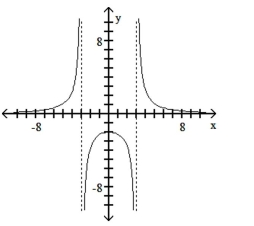
B)
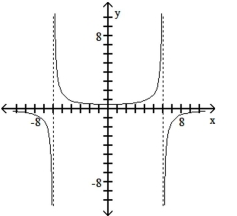
C)
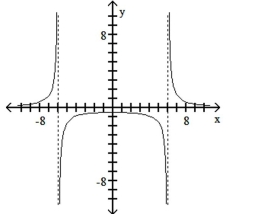
D)
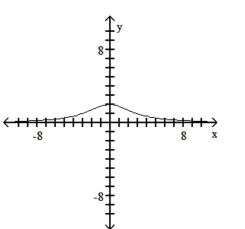
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
7
Match the equation with the appropriate graph.
A)
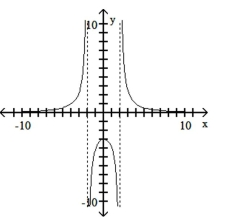
B)
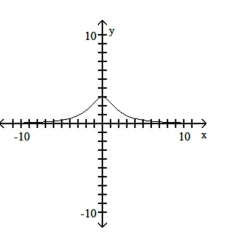
C)
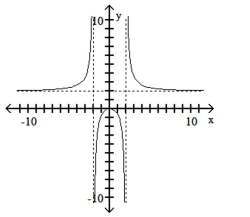
D)
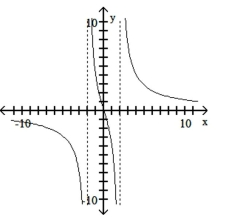
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
8
Match the equation with the appropriate graph.
A)
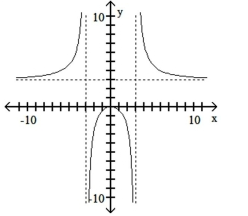
B)
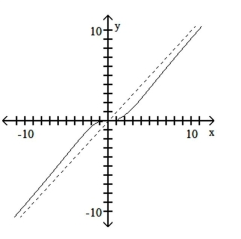
C)
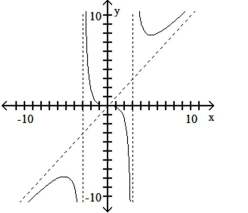
D)
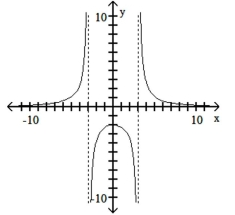
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
9
Use the leading-term test to match the function with the correct graph.
A)
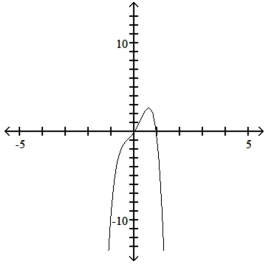
B)
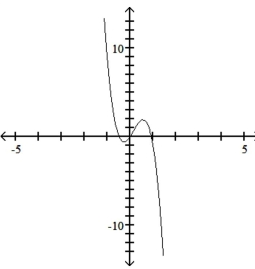
C)
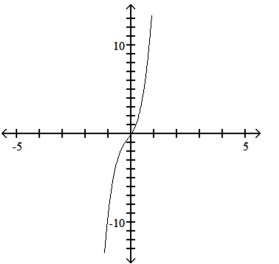
D)
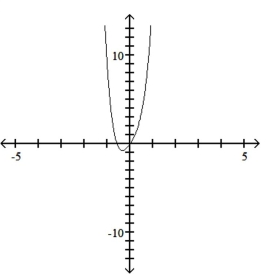
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
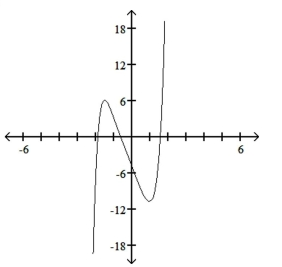
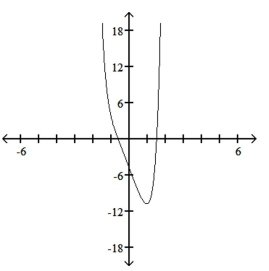
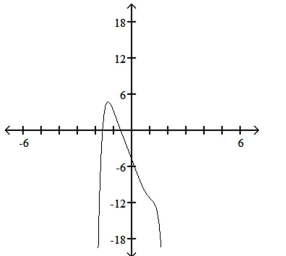
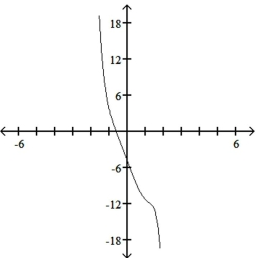
10
Use the leading-term test to match the function with the correct graph.
A)
B)
C)
D)
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the function.
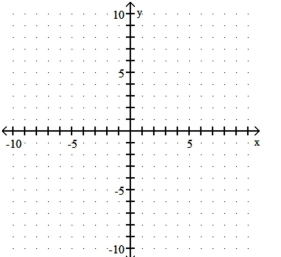
A)
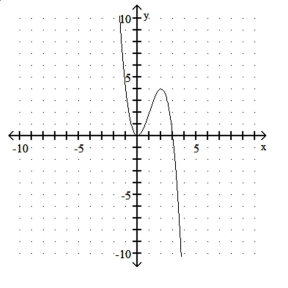
B)
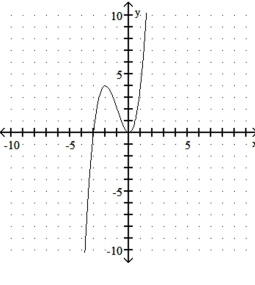
C)
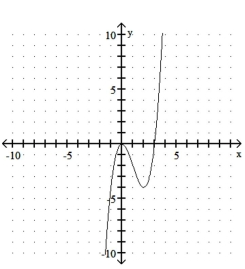
D)
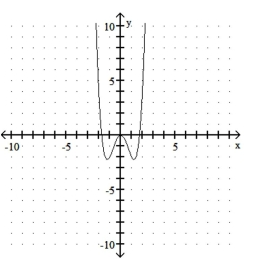

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
12
Use the leading-term test to match the function with the correct graph.
A)
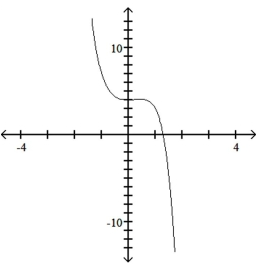
B)
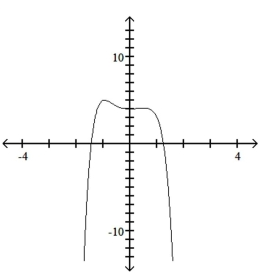
C)
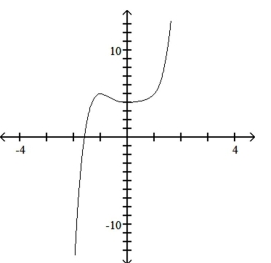
D)
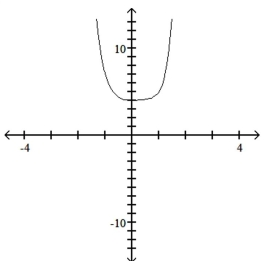
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the given inequality (a related function is graphed).
![<strong>Solve the given inequality (a related function is graphed). \frac { 5 x } { x ^ { 2 } - 9 } \geq 0 </strong> A) ( - 3,0 ) \cup ( 3 , \infty ) B) ( - 3,0 ] \cup ( 3 , \infty ) C) ( - 3 , \infty ) D) ( - \infty , - 3 ) \cup [ 0,3 )](https://storage.examlex.com/TB2705/11ecbb09_9a4d_4e0e_8bc5_f75c974b1dd6_TB2705_11.jpg)
A)
B)
C)
D)
![<strong>Solve the given inequality (a related function is graphed). \frac { 5 x } { x ^ { 2 } - 9 } \geq 0 </strong> A) ( - 3,0 ) \cup ( 3 , \infty ) B) ( - 3,0 ] \cup ( 3 , \infty ) C) ( - 3 , \infty ) D) ( - \infty , - 3 ) \cup [ 0,3 )](https://storage.examlex.com/TB2705/11ecbb09_9a4d_4e0e_8bc5_f75c974b1dd6_TB2705_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
14
Use the leading-term test to match the function with the correct graph.
A)
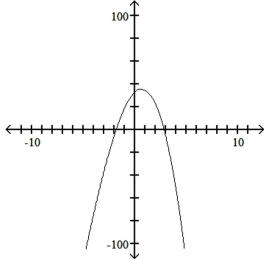
B)
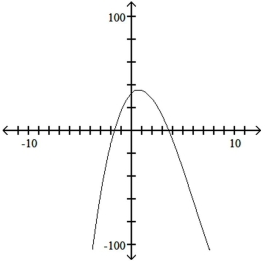
C)
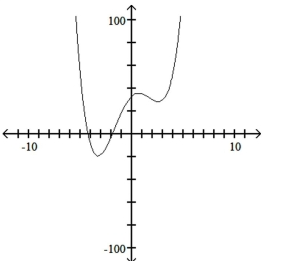
D)
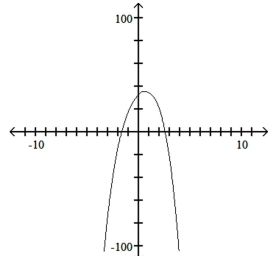
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
15
Find the correct end behavior diagram for the given polynomial function.



Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
16
Use the leading-term test to match the function with the correct graph.
A)
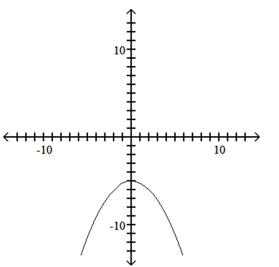
B)
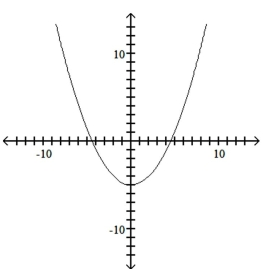
C)

D)
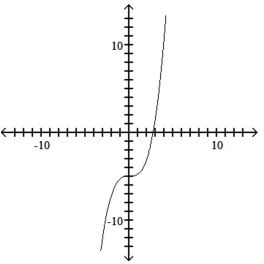
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
17
Match the equation with the appropriate graph.
A)
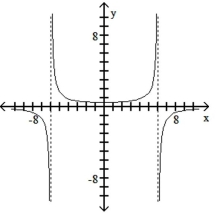
B)
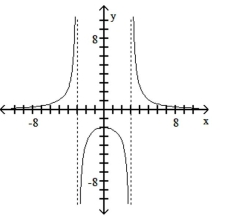
C)
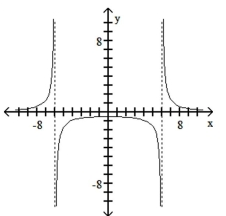
D)
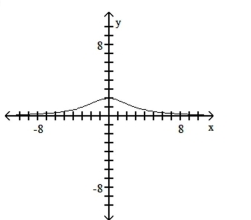
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
18
Match the equation with the appropriate graph.
A)
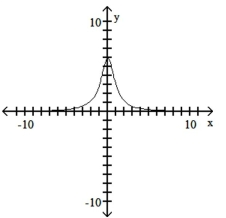
B)
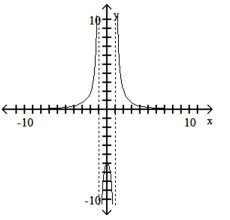
C)
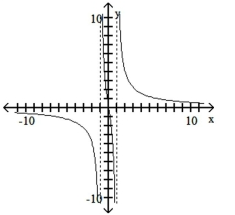
D)
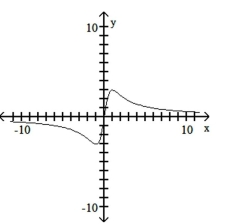
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
19
Match the equation with the appropriate graph.
A)
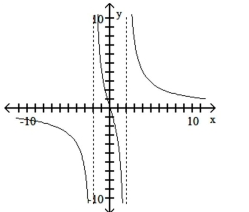
B)
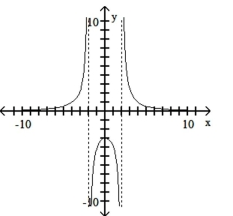
C)
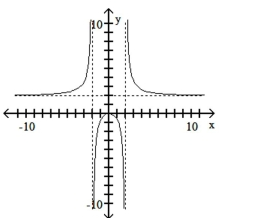
D)
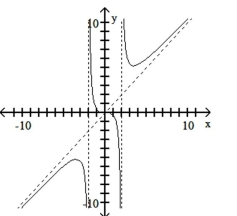
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the function, showing all asymptotes (those that do not correspond to an axis) as dashed lines. List the x- and
y-intercepts.
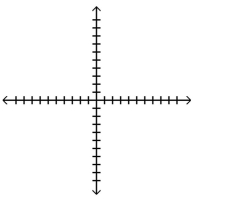
A) x-intercept: -intercept: ;
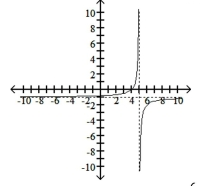
B) x-intercept: -intercept:
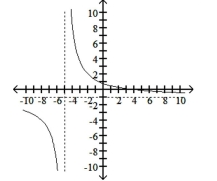
C) -intercept: -intercept: ;
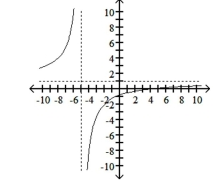
D) -intercept: -intercept: ;
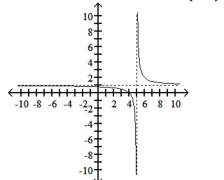
y-intercepts.

A) x-intercept: -intercept: ;

B) x-intercept: -intercept:

C) -intercept: -intercept: ;

D) -intercept: -intercept: ;


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
21
Solve.
The population , in thousands, of Pine Grove is given by , where is the time, in months. Find the interval on which the population was 40 thousand or greater.
A)
B)
C)
D)
The population , in thousands, of Pine Grove is given by , where is the time, in months. Find the interval on which the population was 40 thousand or greater.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the problem.
Assume that a person's threshold weight , defined as the weight above which the risk of death rises dramatically, is given by , where is in pounds and is the person's height in inches. Find the threshold weight for a person who is in. tall. Round your answer to the nearest pound.
A)
B)
C)
D)
Assume that a person's threshold weight , defined as the weight above which the risk of death rises dramatically, is given by , where is in pounds and is the person's height in inches. Find the threshold weight for a person who is in. tall. Round your answer to the nearest pound.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the problem.
The position of an object moving in a straight line is given by , where is in meters and is the time in seconds the object has been in motion. How far will an object move in 20 seconds?
A)
B)
C)
D)
The position of an object moving in a straight line is given by , where is in meters and is the time in seconds the object has been in motion. How far will an object move in 20 seconds?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
24
Find the oblique asymptote, if any, of the rational function.
A)
B)
C) None
D)
A)
B)
C) None
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
25
Use synthetic division to find the function value.
A)
B) 104
C)
D) 96
A)
B) 104
C)
D) 96

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
26
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
27
Using synthetic division, determine whether the numbers are zeros of the polynomial.
A) No; no
B) No; yes
C) Yes; no
D) Yes; yes
A) No; no
B) No; yes
C) Yes; no
D) Yes; yes

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the problem.
If there are teams in a sports league and all the teams play each other twice, a total of games are played, where . A soccer league has 6 teams, each of which plays the others twice. If the league pays per game for the field and officials, how much will it cost to play the entire schedule?
A)
B)
C)
D)
If there are teams in a sports league and all the teams play each other twice, a total of games are played, where . A soccer league has 6 teams, each of which plays the others twice. If the league pays per game for the field and officials, how much will it cost to play the entire schedule?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
29
Find the zeros of the polynomial function and state the multiplicity of each.
A) , multiplicity , multiplicity , multiplicity 1
B) , multiplicity 1 ; 1 , multiplicity 1 ; 5 , multiplicity 1
C) , multiplicity , multiplicity , multiplicity , multiplicity 1
D) , multiplicity , multiplicity , multiplicity 1
A) , multiplicity , multiplicity , multiplicity 1
B) , multiplicity 1 ; 1 , multiplicity 1 ; 5 , multiplicity 1
C) , multiplicity , multiplicity , multiplicity , multiplicity 1
D) , multiplicity , multiplicity , multiplicity 1

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
30
Graph the function, showing all asymptotes (those that do not correspond to an axis) as dashed lines. List the x- and
y-intercepts.
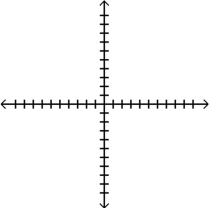
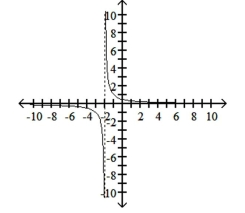
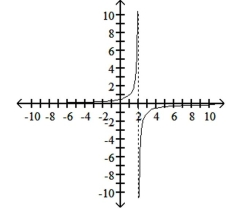
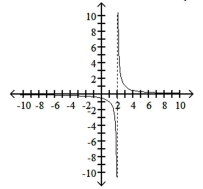
D)
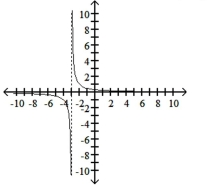
y-intercepts.




D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
31
Find the requested polynomial.
Find a polynomial function of degree 3 with 2, i, -i as zeros. A)
B)
C)
D)
Find a polynomial function of degree 3 with 2, i, -i as zeros. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
32
Find the correct end behavior diagram for the given polynomial function.



Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
33
Solve.
An open-top rectangular box has a square base and it will hold 103 cubic centimeters (cc). Each side of the base has length , and the box has a height of . Express the surface area as a function of the length of a side of the base.
A)
B)
C)
D)
An open-top rectangular box has a square base and it will hold 103 cubic centimeters (cc). Each side of the base has length , and the box has a height of . Express the surface area as a function of the length of a side of the base.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
34
Sketch the graph of the polynomial function. Use the rational zeros theorem when finding the zeros.
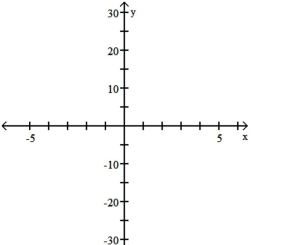
A)
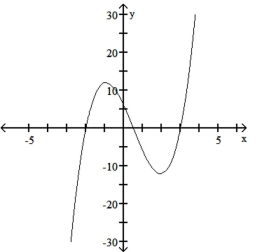
B)
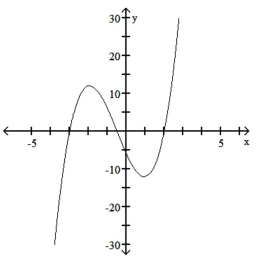
C)
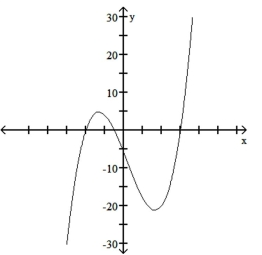
D)
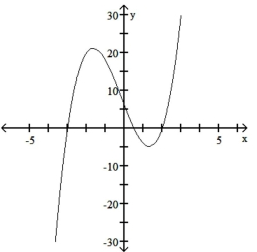

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
35
Solve.
The profit made when units are sold is given by for . Determine the values of for which (a loss is taken).
A)
B)
C)
D)
The profit made when units are sold is given by for . Determine the values of for which (a loss is taken).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
36
Use long division to determine whether the binomial is a factor of f(x).
A) Yes
B)
A) Yes
B)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
37
List the critical values of the related function. Then solve the inequality.
A)
B)
C) No critical values;
D)
A)
B)
C) No critical values;
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the inequality.
For the function , solve .
A)
B)
C)
D)
For the function , solve .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
39
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
40
Use Descartes' Rule of Signs to determine the possible number of positive real zeros and the possible number of negative
real zeros for the function.
A) 0 , 2, or 4 positive; 0 , 2 , or 4 negative
B) 0 or 2 positive; 0,2 , or 4 negative
C) 0 or 2 positive; 0 negative
D) 0,2 , or 4 positive; 0 negative
real zeros for the function.
A) 0 , 2, or 4 positive; 0 , 2 , or 4 negative
B) 0 or 2 positive; 0,2 , or 4 negative
C) 0 or 2 positive; 0 negative
D) 0,2 , or 4 positive; 0 negative

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
41
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
42
Use substitution to determine whether the given number is a zero of the given polynomial.
3;
A) Yes
B)
3;
A) Yes
B)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
43
Find the horizontal asymptote, if any, of the rational function.
A)
B)
C)
D) None
A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
44
Classify the polynomial as constant, linear, quadratic, cubic, or quartic, and determine the leading term, the leading
coefficient, and the degree of the polynomial.
A) Constant;
B) Linear;
C) Linear;
D) Quadratic;
coefficient, and the degree of the polynomial.
A) Constant;
B) Linear;
C) Linear;
D) Quadratic;

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
45
Use synthetic division to find the function value.
; find .
A)
B)
C)
D)
; find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
46
Solve.
There are people in a room. The number of possible handshakes by all the people in the room is given by the function . For what number n of people is ?
A)
B)
C)
D)
There are people in a room. The number of possible handshakes by all the people in the room is given by the function . For what number n of people is ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
47
Graph the polynomial function. Use synthetic division and the remainder theorem to find the zeros.
A) ;
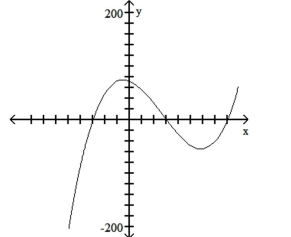
B) ;
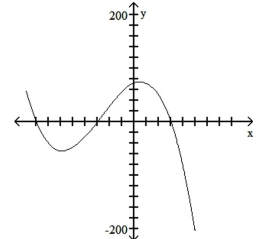
C) (multiplicity 2), 8 ;
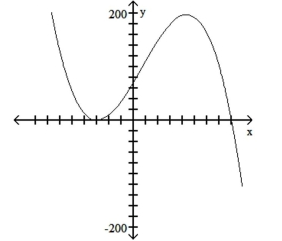
D) (multiplicity 2), ;
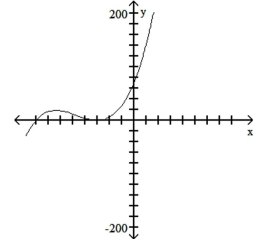

A) ;

B) ;

C) (multiplicity 2), 8 ;

D) (multiplicity 2), ;


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
48
Find the horizontal asymptote, if any, of the rational function.
A)
B)
C)
D) None
A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
49
Given that the polynomial function has the given zero, find the other zeros.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
50
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
51
Use synthetic division to find the quotient and the remainder.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
52
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
53
Find only the rational zeros.
A)
B) 7,1
C)
D) No rational zeros
A)
B) 7,1
C)
D) No rational zeros

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
54
Graph the function, showing all asymptotes (those that do not correspond to an axis) as dashed lines. List the x- and
y-intercepts.
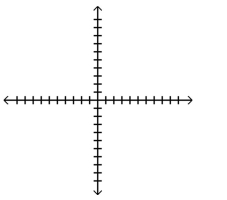
A) -intercepts: and -intercept:
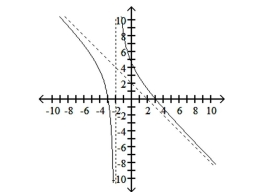
B) -intercepts: and -intercept:
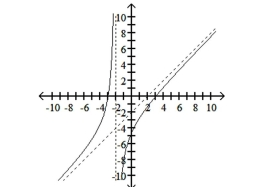
C) x-intercept: -intercept: ;
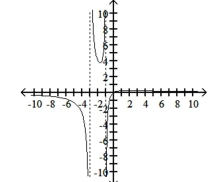
D) -intercept: -intercept: ;
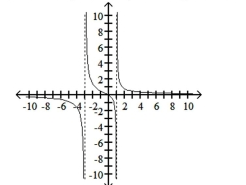
y-intercepts.

A) -intercepts: and -intercept:

B) -intercepts: and -intercept:

C) x-intercept: -intercept: ;

D) -intercept: -intercept: ;


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
55
Find the zeros of the polynomial function and state the multiplicity of each.
A) 2 , multiplicity , multiplicity 1
B) , multiplicity , multiplicity 1
C) -2, multiplicity , multiplicity 2
D) , multiplicity , multiplicity 1
A) 2 , multiplicity , multiplicity 1
B) , multiplicity , multiplicity 1
C) -2, multiplicity , multiplicity 2
D) , multiplicity , multiplicity 1

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
56
Find the correct end behavior diagram for the given polynomial function.
A)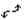
B)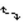
C)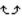
D)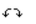
A)
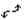
B)
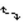
C)
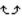
D)
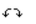

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
57
For the function find the maximum number of real zeros that the function can have, the maximum number of x-intercepts
that the function can have, and the maximum number of turning points that the graph of the function can have.
A)
B)
C)
D)
that the function can have, and the maximum number of turning points that the graph of the function can have.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
58
Classify the polynomial as constant, linear, quadratic, cubic, or quartic, and determine the leading term, the leading
coefficient, and the degree of the polynomial.
A) Constant;
B) Cubic;
C) Cubic;
D) Quadratic;
coefficient, and the degree of the polynomial.
A) Constant;
B) Cubic;
C) Cubic;
D) Quadratic;

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
59
Use substitution to determine whether the given number is a zero of the given polynomial.
A) Yes
B) No
A) Yes
B) No

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
60
Solve.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
61
State the domain of the rational function.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
62
Solve.
An open-top rectangular box has a square base and it will hold 256 cubic centimeters (cc). Each side of the base has length . The box's surface area is given by
Estimate the minimum surface area and the value of that will yield it.
A) when
B) when
C) when
D) when
An open-top rectangular box has a square base and it will hold 256 cubic centimeters (cc). Each side of the base has length . The box's surface area is given by
Estimate the minimum surface area and the value of that will yield it.
A) when
B) when
C) when
D) when

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
63
Find only the rational zeros.
A)
B)
C)
D) No rational zeros
A)
B)
C)
D) No rational zeros

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
64
Find the horizontal asymptote, if any, of the rational function.
A)
B)
C)
D) None
A)
B)
C)
D) None

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
65
Provide the requested response.
Suppose that a polynomial function of degree 5 with rational coefficients has as zeros. Find the other zero(s).
A)
B)
C)
D)
Suppose that a polynomial function of degree 5 with rational coefficients has as zeros. Find the other zero(s).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
66
Use long division to determine whether the binomial is a factor of f(x).
A) Yes
B)
A) Yes
B)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
67
For the function find the maximum number of real zeros that the function can have, the maximum number of x-intercepts
that the function can have, and the maximum number of turning points that the graph of the function can have.
A)
B)
C)
D)
that the function can have, and the maximum number of turning points that the graph of the function can have.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
68
List the critical values of the related function. Then solve the inequality.
A) No critical values;
B)
C) No critical values;
D)
A) No critical values;
B)
C) No critical values;
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
69
Factor the polynomial f(x). Then solve the equation f(x) = 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
70
Graph the function, showing all asymptotes (those that do not correspond to an axis) as dashed lines. List the x- and
y-intercepts.
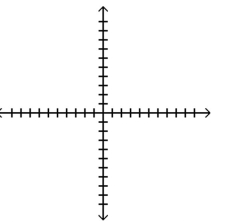
A) No -intercepts, -intercept: ;
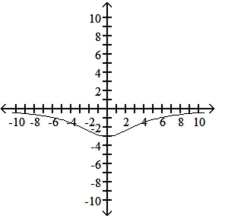
B) No -intercepts, -intercept: ;
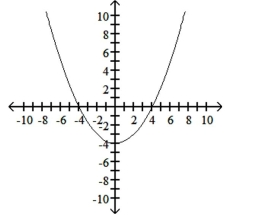
C) x-intercepts: and ,
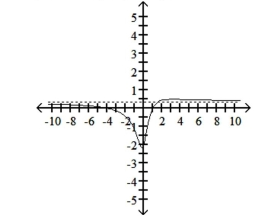
D) x-intercepts: and , y-intercept: ; -intercept: ;
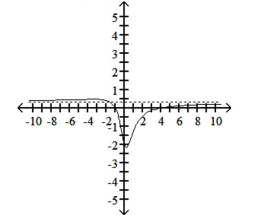
y-intercepts.

A) No -intercepts, -intercept: ;

B) No -intercepts, -intercept: ;

C) x-intercepts: and ,

D) x-intercepts: and , y-intercept: ; -intercept: ;


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
71
List the critical values of the related function. Then solve the inequality.
A)
B)
C) No critical values;
D)
A)
B)
C) No critical values;
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
72
Graph the function.
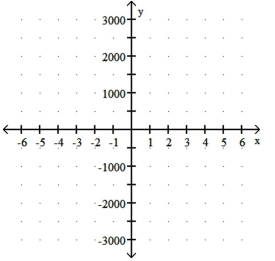
A)
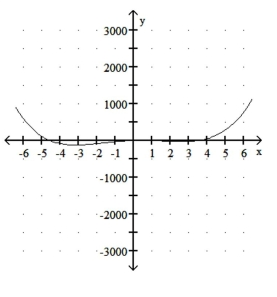
B)
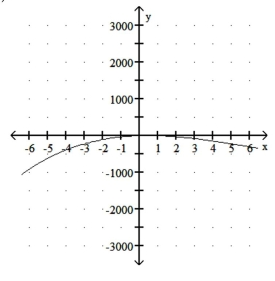
C)
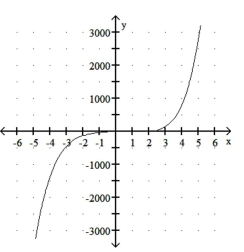
D)
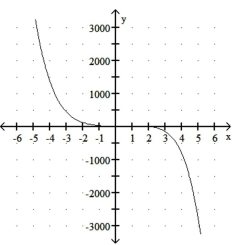

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
73
Provide the requested response.
Suppose that a polynomial function of degree 4 with rational coefficients has 6, 4, 3i as zeros. Find the other zero.
A)3- i
B)- 3i
C)-6
Suppose that a polynomial function of degree 4 with rational coefficients has 6, 4, 3i as zeros. Find the other zero.
A)3- i
B)- 3i
C)-6

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
74
Solve.
The average cost per tape, in dollars, for a company to produce x sports videotapes is given by the function
Graph the function on the interval and complete the following:
A)
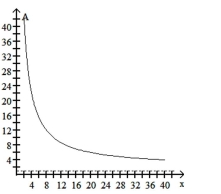
as .
B)
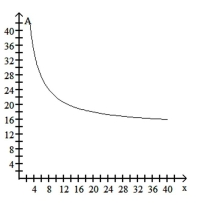
as
C)
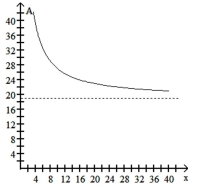
as
D)
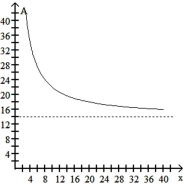
as .
The average cost per tape, in dollars, for a company to produce x sports videotapes is given by the function
Graph the function on the interval and complete the following:
A)

as .
B)

as
C)

as
D)

as .

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
75
Find a rational function that satisfies the given conditions. Answers may vary, but try to give the simplest answer
possible.
Oblique asymptote
A)
B)
C)
D)
possible.
Oblique asymptote
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
76
Classify the polynomial as constant, linear, quadratic, cubic, or quartic, and determine the leading term, the leading
coefficient, and the degree of the polynomial.
A) Linear;
B) Quadratic;
C) Cubic;
D) Linear;
coefficient, and the degree of the polynomial.
A) Linear;
B) Quadratic;
C) Cubic;
D) Linear;

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
77
Given that the polynomial function has the given zero, find the other zeros.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
78
Given that the polynomial function has the given zero, find the other zeros.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the inequality.
For the function , solve .
A)
B)
C)
D)
For the function , solve .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck
80
Use synthetic division to find the function value.
find
A)
B) 284
C)
D)
find
A)
B) 284
C)
D)

Unlock Deck
Unlock for access to all 94 flashcards in this deck.
Unlock Deck
k this deck


