Deck 3: Systems of Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/104
Play
Full screen (f)
Deck 3: Systems of Linear Equations
1
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)
C
2
Determine whether the given ordered pair is a solution to the system.
A) not a solution
B) solution
A) not a solution
B) solution
B
3
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)
B
4
Solve the problem.
The graph shows the results of an ongoing survey of 500 random students at State University from 2007 through 2012. The survey asked whether students bought the majority of their music on CD or if they downloaded the majority of their music as MP3 files from the internet. Use the graph to estimate the point of intersection. In what year was the number of students who bought the majority of their music on CDs and the number of students who downloaded the majority of their music as MP3 files the same? How many students were there for each? A) (2011, 250); 2011; 250 students B) (2010, 300); 2011; 300 students C) (2010, 250); 2010; 250 students D) (2011, 200); 2011; 200 students
A) (2011, 250); 2011; 250 students B) (2010, 300); 2011; 300 students C) (2010, 250); 2010; 250 students D) (2011, 200); 2011; 200 students
The graph shows the results of an ongoing survey of 500 random students at State University from 2007 through 2012. The survey asked whether students bought the majority of their music on CD or if they downloaded the majority of their music as MP3 files from the internet. Use the graph to estimate the point of intersection. In what year was the number of students who bought the majority of their music on CDs and the number of students who downloaded the majority of their music as MP3 files the same? How many students were there for each?
 A) (2011, 250); 2011; 250 students B) (2010, 300); 2011; 300 students C) (2010, 250); 2010; 250 students D) (2011, 200); 2011; 200 students
A) (2011, 250); 2011; 250 students B) (2010, 300); 2011; 300 students C) (2010, 250); 2010; 250 students D) (2011, 200); 2011; 200 students
Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the given ordered pair is a solution to the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the system by graphing.
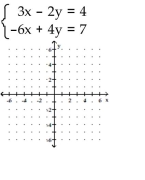 A)
A)
B)
C)
D)
 A)
A) B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
8
Determine whether the given ordered pair is a solution to the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system by graphing.
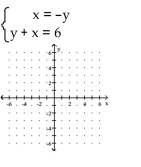 A)
A)
B)
C)
D)
 A)
A) B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system by graphing.
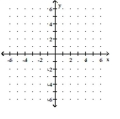
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether the given ordered pair is a solution to the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by graphing.
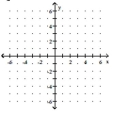
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system by graphing.
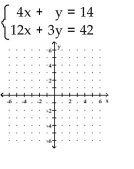
A) {(0, 14)}
B) Ø
C) {(5, -6)}
D) {(x, y) 4x + y = 14}

A) {(0, 14)}
B) Ø
C) {(5, -6)}
D) {(x, y) 4x + y = 14}

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system by graphing.
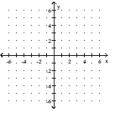
A) {(9, 4)}
B) Ø
C) {(x, y) 3x + y = 13}
D) {(6, 10)}

A) {(9, 4)}
B) Ø
C) {(x, y) 3x + y = 13}
D) {(6, 10)}

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
16
Determine whether the given ordered pair is a solution to the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the system by graphing.
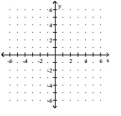
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the system by the substitution method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the system by any method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the system by any method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the system by any method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the system by any method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the system by the substitution method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the problem.
A company's expenses included many factors. In 2012, travel costs were 2.62% of the expense budget, increasing by 0.22% of the total expense budget per year. In 2012, office supplies were 5.71% of the expense budget, increasing by 0.05% of the total expense budget per year. Write a system of equations with two functions. Write one function that models the cost of travel as a percentage of the total expense budget x years after 2012, and another function that models the cost of office supplies as a percentage of the total expense budget x years after 2012. A)
B)
C)
D)
A company's expenses included many factors. In 2012, travel costs were 2.62% of the expense budget, increasing by 0.22% of the total expense budget per year. In 2012, office supplies were 5.71% of the expense budget, increasing by 0.05% of the total expense budget per year. Write a system of equations with two functions. Write one function that models the cost of travel as a percentage of the total expense budget x years after 2012, and another function that models the cost of office supplies as a percentage of the total expense budget x years after 2012. A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
A company's expenses included many factors. In 2012, travel costs were 2.97% of the expense budget , increasing by 0.21% of the total expense budget per year. In 2012, office supplies were 5.80% of the expense budget, increasing by 0.03% of the total expense budget per year. In which year will the cost of travel expenses and office supplies be the same? For that year, what will be the cost of each expense as a percentage of the total expense budget?
A) 2030; 6.8
B) 2028; 6.3
C) 2027; 6.1
D) 2026; 5.9
A company's expenses included many factors. In 2012, travel costs were 2.97% of the expense budget , increasing by 0.21% of the total expense budget per year. In 2012, office supplies were 5.80% of the expense budget, increasing by 0.03% of the total expense budget per year. In which year will the cost of travel expenses and office supplies be the same? For that year, what will be the cost of each expense as a percentage of the total expense budget?
A) 2030; 6.8
B) 2028; 6.3
C) 2027; 6.1
D) 2026; 5.9

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the system by any method.
A)
В)
C)
D)
A)
В)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the system by the addition method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 10 feet more than 2 times the width. He needs 68 feet of fencing to do the job. Find the length and width of the garden. A) length: ; width:
B) length: ; width:
C) length: ; width:
D) length: ; width:
Jarod is having a problem with rabbits getting into his vegetable garden, so he decides to fence it in. The length of the garden is 10 feet more than 2 times the width. He needs 68 feet of fencing to do the job. Find the length and width of the garden. A) length: ; width:
B) length: ; width:
C) length: ; width:
D) length: ; width:

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
A chemist needs 150 milliliters of a 45% solution but has only 25% and 55% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 100 milliliters of 25%; 50 milliliters of 55%
B) 60 milliliters of 25%; 100 milliliters of 55%
C) 50 milliliters of 25%; 100 milliliters of 55%
D) 60 milliliters of 25%; 110 milliliters of 55%
A chemist needs 150 milliliters of a 45% solution but has only 25% and 55% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 100 milliliters of 25%; 50 milliliters of 55%
B) 60 milliliters of 25%; 100 milliliters of 55%
C) 50 milliliters of 25%; 100 milliliters of 55%
D) 60 milliliters of 25%; 110 milliliters of 55%

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the system by any method.
A) infinitely many solutions
B) one ordered-pair solution
C) no solution
A) infinitely many solutions
B) one ordered-pair solution
C) no solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
An electronics company kept comparative statistics on two products, A and B. For the years 2003 to 2011, the total number of Product A ever sold (in thousands) is given by the equation y = 74x + 250, where x is the number of years since 2003. For that same period, the total number of Product B ever sold (in thousands) is given by the equation y = -30x + 434, where x is the number of years since 2003. Use the substitution method to solve the system and choose the statement that most accurately describes the solution. A) At some point between 2003 and 2011, the company had sold 1800 of each product. B) The company sold about 1.8 times as many of Product B as Product A. C) When 383,000 of Product A had been sold, 1.8 times as many of Product B had been sold. D) At about 1.8 years (to the nearest tenth) since 2003, the company sold the same number of Product A as Product B.
An electronics company kept comparative statistics on two products, A and B. For the years 2003 to 2011, the total number of Product A ever sold (in thousands) is given by the equation y = 74x + 250, where x is the number of years since 2003. For that same period, the total number of Product B ever sold (in thousands) is given by the equation y = -30x + 434, where x is the number of years since 2003. Use the substitution method to solve the system and choose the statement that most accurately describes the solution. A) At some point between 2003 and 2011, the company had sold 1800 of each product. B) The company sold about 1.8 times as many of Product B as Product A. C) When 383,000 of Product A had been sold, 1.8 times as many of Product B had been sold. D) At about 1.8 years (to the nearest tenth) since 2003, the company sold the same number of Product A as Product B.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the system by any method.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
Julie and Eric row their boat (at a constant speed) 24 miles downstream for 4 hours, helped by the current. Rowing at the same rate, the trip back against the current takes 6 hours. Find the rate of the current.
A) 2 mph
B) 1 mph
C) 0.5 mph
D) 5 mph
Julie and Eric row their boat (at a constant speed) 24 miles downstream for 4 hours, helped by the current. Rowing at the same rate, the trip back against the current takes 6 hours. Find the rate of the current.
A) 2 mph
B) 1 mph
C) 0.5 mph
D) 5 mph

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
A couple have bought a new house and are comparing quotes from two moving companies for moving their furniture. Company A charges $120 for the truck and $55 per hour for the movers. Company B charges $110 for the truck and $70 per hour for the movers. Create a cost equation for each company where y is the total cost and x is the number of hours of labor. Write a system of equations.
A) 55y = 120x
B) 55y = x + 120
C) y = 55x + 120
D) y = 120x + 55 70y = 110x 70y = x + 110 y = 70x + 110 y = 110x + 70
A couple have bought a new house and are comparing quotes from two moving companies for moving their furniture. Company A charges $120 for the truck and $55 per hour for the movers. Company B charges $110 for the truck and $70 per hour for the movers. Create a cost equation for each company where y is the total cost and x is the number of hours of labor. Write a system of equations.
A) 55y = 120x
B) 55y = x + 120
C) y = 55x + 120
D) y = 120x + 55 70y = 110x 70y = x + 110 y = 70x + 110 y = 110x + 70

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
A flat rectangular piece of aluminum has a perimeter of 56 inches. The length is 6 inches longer than the width. Find the width.
A) 11 in.
B) 28 in.
C) 17 in.
D) 23 in.
A flat rectangular piece of aluminum has a perimeter of 56 inches. The length is 6 inches longer than the width. Find the width.
A) 11 in.
B) 28 in.
C) 17 in.
D) 23 in.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
One number is 3 less than a second number. Twice the second number is 2 less than 4 times the first. Find the two numbers.
A) 4 and 7
B) 5 and 8
C) -7 and -4
D) 3 and 6
One number is 3 less than a second number. Twice the second number is 2 less than 4 times the first. Find the two numbers.
A) 4 and 7
B) 5 and 8
C) -7 and -4
D) 3 and 6

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $6.00. Another customer buys 5 hot dogs and 4 bags of potato chips for $13.75. Find the cost of each item.
A) $2.00 for a hot dog; $1.50 for a bag of potato chips
B) $1.75 for a hot dog; $1.50 for a bag of potato chips
C) $1.25 for a hot dog; $1.75 for a bag of potato chips
D) $1.75 for a hot dog; $1.25 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $6.00. Another customer buys 5 hot dogs and 4 bags of potato chips for $13.75. Find the cost of each item.
A) $2.00 for a hot dog; $1.50 for a bag of potato chips
B) $1.75 for a hot dog; $1.50 for a bag of potato chips
C) $1.25 for a hot dog; $1.75 for a bag of potato chips
D) $1.75 for a hot dog; $1.25 for a bag of potato chips

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
A twin-engined aircraft can fly 672 miles from city A to city B in 3 hours with the wind and make the return trip in 7 hours against the wind. What is the speed of the wind?
A) 96 mph
B) 48 mph
C) 80 mph
D) 64 mph
A twin-engined aircraft can fly 672 miles from city A to city B in 3 hours with the wind and make the return trip in 7 hours against the wind. What is the speed of the wind?
A) 96 mph
B) 48 mph
C) 80 mph
D) 64 mph

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
A bank teller has 53 $20 and $5 bills in her cash drawer. The value of the bills is $490. How many $20 bills are there?
A) 38 $20 bills
B) 36 $20 bills
C) 17 $20 bills
D) 15 $20 bills
A bank teller has 53 $20 and $5 bills in her cash drawer. The value of the bills is $490. How many $20 bills are there?
A) 38 $20 bills
B) 36 $20 bills
C) 17 $20 bills
D) 15 $20 bills

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the problem.
Andrea is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $190 for materials and equipment rental plus $50 per hour for labor. Company B gave an estimate of $260 for materials and equipment rental plus $40 per hour for labor. Create a cost equation for each company where y is the total cost of the landscaping and x is the number of hours of labor. Determine how many hours of labor will be required for the two companies to cost the same.
A) 11 hr
B) 10 hr
C) 6 hr
D) 7 hr
Andrea is having her yard landscaped. She obtained an estimate from two landscaping companies. Company A gave an estimate of $190 for materials and equipment rental plus $50 per hour for labor. Company B gave an estimate of $260 for materials and equipment rental plus $40 per hour for labor. Create a cost equation for each company where y is the total cost of the landscaping and x is the number of hours of labor. Determine how many hours of labor will be required for the two companies to cost the same.
A) 11 hr
B) 10 hr
C) 6 hr
D) 7 hr

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
A retired couple has $170,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 5%. The rest they want to invest in AA bonds yielding 11% per year. How much should they invest in each to realize exactly $15,700 per year?
A) $120,000 at 11% and $50,000 at 5%
B) $110,000 at 5% and $60,000 at 11%
C) $120,000 at 5% and $50,000 at 11%
D) $130,000 at 11% and $40,000 at 5%
A retired couple has $170,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 5%. The rest they want to invest in AA bonds yielding 11% per year. How much should they invest in each to realize exactly $15,700 per year?
A) $120,000 at 11% and $50,000 at 5%
B) $110,000 at 5% and $60,000 at 11%
C) $120,000 at 5% and $50,000 at 11%
D) $130,000 at 11% and $40,000 at 5%

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is $3.40 more than the value of the nickels. How many nickels and dimes does Jamil have?
A) 3 nickels and 27 dimes
B) 5 nickels and 45 dimes
C) 4 nickels and 36 dimes
D) 36 nickels and 4 dimes
Jamil always throws loose change into a pencil holder on his desk and takes it out every two weeks. This time it is all nickels and dimes. There are 9 times as many dimes as nickels, and the value of the dimes is $3.40 more than the value of the nickels. How many nickels and dimes does Jamil have?
A) 3 nickels and 27 dimes
B) 5 nickels and 45 dimes
C) 4 nickels and 36 dimes
D) 36 nickels and 4 dimes

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the system by any method.
A) one ordered-pair solution
B) infinitely many solutions
C) no solution
A) one ordered-pair solution
B) infinitely many solutions
C) no solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
One number is 4 less than a second number. Twice the second number is 17 more than 3 times the first. Find the two numbers.
A) 5 and 9
B) -10 and -6
C) -8 and -4
D) -9 and -5
One number is 4 less than a second number. Twice the second number is 17 more than 3 times the first. Find the two numbers.
A) 5 and 9
B) -10 and -6
C) -8 and -4
D) -9 and -5

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
Devon purchased tickets to an air show for 8 adults and 2 children. The total cost was $170. The cost of a child's ticket was $5 less than the cost of an adult's ticket. Find the price of an adult's ticket and a child's ticket.
A) adult's ticket: $18; child's ticket: $13
B) adult's ticket: $20; child's ticket: $15
C) adult's ticket: $17; child's ticket: $12
D) adult's ticket: $19; child's ticket: $14
Devon purchased tickets to an air show for 8 adults and 2 children. The total cost was $170. The cost of a child's ticket was $5 less than the cost of an adult's ticket. Find the price of an adult's ticket and a child's ticket.
A) adult's ticket: $18; child's ticket: $13
B) adult's ticket: $20; child's ticket: $15
C) adult's ticket: $17; child's ticket: $12
D) adult's ticket: $19; child's ticket: $14

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
A college student earned $8400 during summer vacation working as a waiter in a popular restaurant. The student invested part of the money at 10% and the rest at 8%. If the student received a total of $720 in interest at the end of the year, how much was invested at 10%?
A) $4200
B) $1050
C) $2400
D) $6000
A college student earned $8400 during summer vacation working as a waiter in a popular restaurant. The student invested part of the money at 10% and the rest at 8%. If the student received a total of $720 in interest at the end of the year, how much was invested at 10%?
A) $4200
B) $1050
C) $2400
D) $6000

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 1200 units
B) 445 units
C) 1201 units
D) 1202 units en.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 1200 units
B) 445 units
C) 1201 units
D) 1202 units en.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
62
Determine if the given ordered triple is a solution of the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
63
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 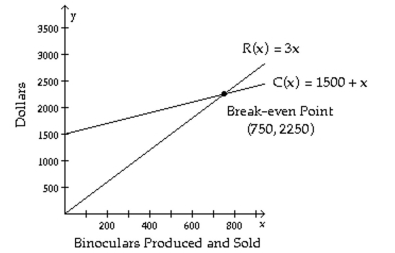
What is the profit when 878 binoculars are produced?
A) $3256
B) $2012
C) $256
D) $5012

What is the profit when 878 binoculars are produced?
A) $3256
B) $2012
C) $256
D) $5012

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 62 units
B) 60 units
C) 61 units
D) 11 units en.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 62 units
B) 60 units
C) 61 units
D) 11 units en.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
67
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
How many binoculars must be produced and sold for the company to break even?
A) 750 binoculars
B) 2250 binoculars
C) 2700 binoculars
D) 1500 binoculars

How many binoculars must be produced and sold for the company to break even?
A) 750 binoculars
B) 2250 binoculars
C) 2700 binoculars
D) 1500 binoculars

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
68
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
More than how many binoculars must be produced and sold for the company to have a profit gain?
A) 2700 binoculars
B) 1500 binoculars
C) 750 binoculars
D) 2250 binoculars

More than how many binoculars must be produced and sold for the company to have a profit gain?
A) 2700 binoculars
B) 1500 binoculars
C) 750 binoculars
D) 2250 binoculars

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
69
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
Fewer than how many binoculars must be produced and sold for the company to have a profit loss?
A) 2250 binoculars
B) 750 binoculars
C) 1500 binoculars
D) 2700 binoculars

Fewer than how many binoculars must be produced and sold for the company to have a profit loss?
A) 2250 binoculars
B) 750 binoculars
C) 1500 binoculars
D) 2700 binoculars

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
70
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
Is there a profit when 676 binoculars are produced?
A) Yes
B) No

Is there a profit when 676 binoculars are produced?
A) Yes
B) No

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 11 units
B) 4 units
C) 9 units
D) 10 units en.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 11 units
B) 4 units
C) 9 units
D) 10 units en.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)
Given the cost function, C(x), and the revenue function, R(x), write the profit function from producing and selling x units of the product.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 1400 units
B) 1420 units
C) 337 units
D) 1410 units en.
Given the cost function, , and the revenue function, , find the number of units that must be sold to brea
A) 1400 units
B) 1420 units
C) 337 units
D) 1410 units en.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
75
Determine if the given ordered triple is a solution of the system.
A) solution
B) not a solution
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)
Given the cost function, , and the revenue function, , find the dollar amount coming in and going out at the break-even point. Round to the nearest dollar if necessary.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
77
Determine if the given ordered triple is a solution of the system.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
78
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
Is there a profit when 966 binoculars are produced?
A) Yes
B) No

Is there a profit when 966 binoculars are produced?
A) Yes
B) No

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
79
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
Use the revenue and cost functions to write the profit function from producing and selling x binoculars.
A) P(x) = 4x + 1500
B) P(x) = 2x - 1500
C) P(x) = 4x - 1500
D) P(x) = 2x + 1500

Use the revenue and cost functions to write the profit function from producing and selling x binoculars.
A) P(x) = 4x + 1500
B) P(x) = 2x - 1500
C) P(x) = 4x - 1500
D) P(x) = 2x + 1500

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
80
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use the information in the figure to answer the question. 
At the break-even point both cost and revenue are what?
A) $750
B) $2250
C) $1500
D) $2700

At the break-even point both cost and revenue are what?
A) $750
B) $2250
C) $1500
D) $2700

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck


