Deck 1: Speaking Mathematically
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/13
Play
Full screen (f)
Deck 1: Speaking Mathematically
1
Fill in the blanks to rewrite the following statement with variables:
Given any positive real number, there is a positive real number that is smaller.
(a) Given any positive real number r, there is s such that s is .
(b) For any , such that s < r.
Given any positive real number, there is a positive real number that is smaller.
(a) Given any positive real number r, there is s such that s is .
(b) For any , such that s < r.
a. a positive real number; smaller than r b. positive real number r; there is a positive real number s
Fill in the blanks to rewrite the following statement with variables:
Fill in the blanks to rewrite the following statement with variables:
2
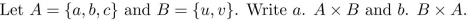
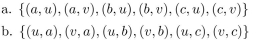
3
Fill in the blanks to rewrite the following statement:
There is a positive integer that is less than or equal to every positive integer.
(a) There is a positive integer m such that m is .
(b) There is a such that every positive integer.
(c) There is a positive integer m which satisfies the property that given any positive integer
n, m is .
There is a positive integer that is less than or equal to every positive integer.
(a) There is a positive integer m such that m is .
(b) There is a such that every positive integer.
(c) There is a positive integer m which satisfies the property that given any positive integer
n, m is .
a. less than or equal to every positive integer
b. positive integer m; less than or equal to every positive integer
c. less than or equal to n
b. positive integer m; less than or equal to every positive integer
c. less than or equal to n
4
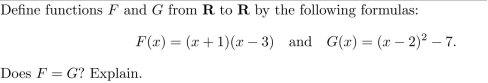

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
5
Fill in the blanks to rewrite the following statement:
For all objects T, if T is a triangle then T has three sides.
(a) All triangles .
(b) Every triangle .
(c) If an object is a triangle, then it .
(d) If T , then T .
(e) For all triangles T, .
For all objects T, if T is a triangle then T has three sides.
(a) All triangles .
(b) Every triangle .
(c) If an object is a triangle, then it .
(d) If T , then T .
(e) For all triangles T, .

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
6
(a) Write in words how to read the following out loud 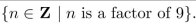
(b) Use the set-roster notation to indicate the elements in the set.
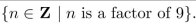
(b) Use the set-roster notation to indicate the elements in the set.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
7
Fill in the blanks to rewrite the following statement:
Every real number has an additive inverse.
(a) All real numbers .
(b) For any real number x, there is for x.
(c) For all real numbers x, there is real number y such that .
Every real number has an additive inverse.
(a) All real numbers .
(b) For any real number x, there is for x.
(c) For all real numbers x, there is real number y such that .

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
8
Rewrite the following statement less formally, without using variables:
There is an integer n such that 1/n is also an integer.
There is an integer n such that 1/n is also an integer.

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
9


Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
10


Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
11
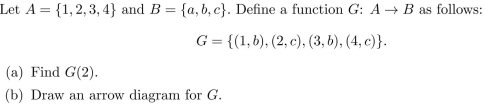

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
12


Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck
13
Fill in the blanks to rewrite the following statement with variables: Is there an integer with a
remainder of 1 when it is divided by 4 and a remainder of 3 when it is divided by 7?
(a) Is there an integer n such that n has ?
(b) Does there exist such that if n is divided by 4 the remainder is 1 and if ?
remainder of 1 when it is divided by 4 and a remainder of 3 when it is divided by 7?
(a) Is there an integer n such that n has ?
(b) Does there exist such that if n is divided by 4 the remainder is 1 and if ?

Unlock Deck
Unlock for access to all 13 flashcards in this deck.
Unlock Deck
k this deck


