Deck 6: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/134
Play
Full screen (f)
Deck 6: Systems of Equations and Inequalities
1
Solve the problem.
The Family Arts Center charges $21 for adults, $13 for senior citizens, and $8 for children under 12 for their live performances on Sunday afternoon. This past Sunday, the paid revenue was $12,388 for 905 tickets sold. There
Were 50 more children than adults. How many children attended?
A) 291 children
B) 341 children
C) 273 children
D) 331 children
The Family Arts Center charges $21 for adults, $13 for senior citizens, and $8 for children under 12 for their live performances on Sunday afternoon. This past Sunday, the paid revenue was $12,388 for 905 tickets sold. There
Were 50 more children than adults. How many children attended?
A) 291 children
B) 341 children
C) 273 children
D) 331 children
B
2
Solve the problem.
An 8-cylinder Crown Victoria gives 18 miles per gallon in city driving and 21 miles per gallon in highway driving. A 300-mile trip required 15.5 gallons of gasoline. How many whole miles were driven in the city?
A) 132 miles
B) 147 miles
C) 168 miles
D) 153 miles
An 8-cylinder Crown Victoria gives 18 miles per gallon in city driving and 21 miles per gallon in highway driving. A 300-mile trip required 15.5 gallons of gasoline. How many whole miles were driven in the city?
A) 132 miles
B) 147 miles
C) 168 miles
D) 153 miles
D
3
Verify that the values of the variables listed are solutions of the system of equations.
x = 3 , y = 1 , z = - 5
A) not a solution
B) solution
x = 3 , y = 1 , z = - 5
A) not a solution
B) solution
B
4
 Solve the system.
Solve the system.A) dependent (many solutions)
B) (2, 4)
C) (2, 3)
D) inconsistent (no solution)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the problem.
Find real numbers a, b, and c such that the graph of the function y = ax2 + bx + c contains the points (1, 1), (2, 4), and (-3, 29).
Find real numbers a, b, and c such that the graph of the function y = ax2 + bx + c contains the points (1, 1), (2, 4), and (-3, 29).

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the problem.
The Family Fine Arts Center charges $24 per adult and $10 per senior citizen for its performances. On a recent weekend evening when 538 people paid admission, the total receipts were $7592. How many who paid were
Senior citizens?
A) 158 senior citizens
B) 290 senior citizens
C) 248 senior citizens
D) 380 senior citizens
The Family Fine Arts Center charges $24 per adult and $10 per senior citizen for its performances. On a recent weekend evening when 538 people paid admission, the total receipts were $7592. How many who paid were
Senior citizens?
A) 158 senior citizens
B) 290 senior citizens
C) 248 senior citizens
D) 380 senior citizens

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
7
Solve the problem.
Lexie wants to have an income of $9000 per year from investments. To that end she is going to invest $90,000 in
three different accounts. These accounts pay 7%, 10%, and 14% simple interest. If she wants to have $10,000
more in the account paying 7% simple interest than she has in the account paying 14% simple interest, how
much should go into each account?
Lexie wants to have an income of $9000 per year from investments. To that end she is going to invest $90,000 in
three different accounts. These accounts pay 7%, 10%, and 14% simple interest. If she wants to have $10,000
more in the account paying 7% simple interest than she has in the account paying 14% simple interest, how
much should go into each account?

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
8
Verify that the values of the variables listed are solutions of the system of equations.
A) not a solution
B) solution
A) not a solution
B) solution

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the problem.
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 8 slices of pizza and 7 soft drinks for $36.53. The second group bought 6 slices of pizza and 5 soft drinks for $
26)93. How much does one slice of pizza cost?
A) $1.87 per slice of pizza
B) $2.37 per slice of pizza
C) $2.43 per slice of pizza
D) $2.93 per slice of pizza
A tour group split into two groups when waiting in line for food at a fast food counter. The first group bought 8 slices of pizza and 7 soft drinks for $36.53. The second group bought 6 slices of pizza and 5 soft drinks for $
26)93. How much does one slice of pizza cost?
A) $1.87 per slice of pizza
B) $2.37 per slice of pizza
C) $2.43 per slice of pizza
D) $2.93 per slice of pizza

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
10
Verify that the values of the variables listed are solutions of the system of equations.
x = 5 , y = - 6
A) solution
B) not a solution
x = 5 , y = - 6
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the problem.
A company has sales (measured in millions of dollars) of 50, 60, and 75 during the first three consecutive years.Find a quadratic function that fits these data, and use the result to predict the sales during the fourth year. Assume that the quadratic function is of the form y = ax2 + bx + c A) ; sales during the fourth year million
B) ; sales during the fourth year million
C) ; sales during the fourth year million
D) ; sales during the fourth year million
A company has sales (measured in millions of dollars) of 50, 60, and 75 during the first three consecutive years.Find a quadratic function that fits these data, and use the result to predict the sales during the fourth year. Assume that the quadratic function is of the form y = ax2 + bx + c A) ; sales during the fourth year million
B) ; sales during the fourth year million
C) ; sales during the fourth year million
D) ; sales during the fourth year million

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system of equations by using substitution.
A) x = 5, y = 2
B) x = -5, y = -2
C) x = -5, y = 2
D) x = 5, y = -2
A) x = 5, y = 2
B) x = -5, y = -2
C) x = -5, y = 2
D) x = 5, y = -2

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
13
Verify that the values of the variables listed are solutions of the system of equations.
x = 0 , y = 5 , z = - 5
A) solution
B) not a solution
x = 0 , y = 5 , z = - 5
A) solution
B) not a solution

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the problem.
A flat rectangular piece of aluminum has a perimeter of 64 inches. The length is 14 inches longer than the width. Find the width.
A) 32 inches
B) 9 inches
C) 37 inches
D) 23 inches
A flat rectangular piece of aluminum has a perimeter of 64 inches. The length is 14 inches longer than the width. Find the width.
A) 32 inches
B) 9 inches
C) 37 inches
D) 23 inches

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
15
Write the augmented matrix for the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the problem.
A movie theater charges $8.00 for adults and $5.00 for children. If there were 40 people altogether and the theater collected $272.00 at the end of the day, how many of them were adults?
A) 10 adults
B) 24 adults
C) 29 adults
D) 16 adults
A movie theater charges $8.00 for adults and $5.00 for children. If there were 40 people altogether and the theater collected $272.00 at the end of the day, how many of them were adults?
A) 10 adults
B) 24 adults
C) 29 adults
D) 16 adults

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
17
Write the augmented matrix for the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the problem.
A retired couple has $140,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 5%. The rest they want to invest in AA bonds yielding 12% per year. How much
Should they invest in each to realize exactly $13,300 per year?
A) $90,000 at 5% and $50,000 at 12%
B) $80,000 at 5% and $60,000 at 12%
C) $90,000 at 12% and $50,000 at 5%
D) $100,000 at 12% and $40,000 at 5%
A retired couple has $140,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 5%. The rest they want to invest in AA bonds yielding 12% per year. How much
Should they invest in each to realize exactly $13,300 per year?
A) $90,000 at 5% and $50,000 at 12%
B) $80,000 at 5% and $60,000 at 12%
C) $90,000 at 12% and $50,000 at 5%
D) $100,000 at 12% and $40,000 at 5%

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the system of equations by using substitution.
A) x = 0, y = 1
B) x = 1, y = 1
C) x = 1, y = 0
D) x = 0, y = 0
A) x = 0, y = 1
B) x = 1, y = 1
C) x = 1, y = 0
D) x = 0, y = 0

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
20
Write the augmented matrix for the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
21
Find the value of the determinant.
A) -12
B) -90
C) 130
D) 80
A) -12
B) -90
C) 130
D) 80

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
22
Perform the row operation(s) on the given augmented matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
23
Find the value of the determinant.
A) x = 3, y = 7, z = 1
B) x = 3, y = -7, z = -1
C) x = 4, y = 5, z = 1
D) x = 7, y = 1, z = 7
A) x = 3, y = 7, z = 1
B) x = 3, y = -7, z = -1
C) x = 4, y = 5, z = 1
D) x = 7, y = 1, z = 7

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the problem.
A) 0
B) 6
C) 9
D) -9
A) 0
B) 6
C) 9
D) -9

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
25
Write the augmented matrix for the system.
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
26
Write the augmented matrix for the system.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
27
Perform the row operation(s) on the given augmented matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
28
Perform the row operation(s) on the given augmented matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
29
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) 14
B) -14
C) 0
D) Cannot determine
A) 14
B) -14
C) 0
D) Cannot determine

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
30
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) 118
B) -118
C) 354
D) -354
A) 118
B) -118
C) 354
D) -354

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
31
Find the value of the determinant.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
32
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) 186
B) -186
C) 62
D) -62
A) 186
B) -186
C) 62
D) -62

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
33
Find the value of the determinant.
A) -20
B) -4
C) 4
D) 34
A) -20
B) -4
C) 4
D) 34

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
34
Perform the row operation(s) on the given augmented matrix.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
35
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) -276
B) -138
C) 276
D) 138
A) -276
B) -138
C) 276
D) 138

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
37
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) -24
B) 3
C) -3
D) 24
A) -24
B) 3
C) -3
D) 24

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
38
Use the properties of determinants to find the value of the second determinant, given the value of the first.
A) -2
B) 4
C) -4
D) 2
A) -2
B) 4
C) -4
D) 2

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
39
Find the value of the determinant.
A) -8
B) -168
C) 8
D) 440
A) -8
B) -168
C) 8
D) 440

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
40
Use the properties of determinants to find the value of the second determinant, given the value of the first.
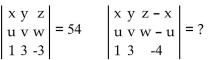
A) -54
B) 0
C) 54
D) Cannot determine
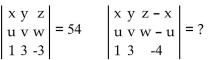
A) -54
B) 0
C) 54
D) Cannot determine

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
41
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
42
Find the inverse of the matrix.
A)
B)
C)
D) No inverse
A)
B)
C)
D) No inverse

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
43
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
45
Find the inverse of the matrix.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
46
Find the inverse of the matrix.
A)
B)
C)
D) No inverse
A)
B)
C)
D) No inverse

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the problem.
Let and . Find .
A)
B)
C)
D)
Let and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
48
Perform the indicated operations and simplify.
Let , and . Find .
A)
B)
C)
D)
Let , and . Find .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
49
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
50
Find the inverse of the matrix.
A)
B)
C)
D) No inverse
A)
B)
C)
D) No inverse

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
51
Find the inverse of the matrix.
A)
B)
C)
D) No inverse
A)
B)
C)
D) No inverse

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
52
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
53
Use a graphing utility to find the inverse of the matrix, if it exists. Round answers to two decimal places, if necessary.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
54
Find the inverse of the matrix.
A)
B)
D)
A)
B)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
55
Find the inverse of the matrix.
A)
B) No inverse
C)
D)
A)
B) No inverse
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
56
Find the inverse of the matrix.
A)
B)
C)
D) No inverse
A)
B)
C)
D) No inverse

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
57
Use a graphing utility to find the inverse of the matrix, if it exists. Round answers to two decimal places, if necessary.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
58
Use a graphing utility to find the inverse of the matrix, if it exists. Round answers to two decimal places, if necessary.
A)
B)
D)
A)
B)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
59
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
60
Find the inverse of the matrix.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the system of equations using substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the system of equations using substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
63
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
64
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
65
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
66
Tell whether the given rational expression is proper or improper.
A) Improper
B) Proper
A) Improper
B) Proper

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
67
Tell whether the given rational expression is proper or improper.
A) Proper
B) Improper
A) Proper
B) Improper

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
68
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
69
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the system of equations using substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
71
Write the partial fraction decomposition of the rational expression.

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
72
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
73
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
74
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
75
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
76
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
77
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the system of equations using substitution.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
79
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck
80
Write the partial fraction decomposition of the rational expression.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 134 flashcards in this deck.
Unlock Deck
k this deck


