Deck 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/29
Play
Full screen (f)
Deck 14: Mathematics Problem Set: Set Theory, Number Theory, Combinatorics, and Boolean Algebra
1
Use mathematical induction to prove that n! ≥ 2n−1 whenever n is a positive integer.
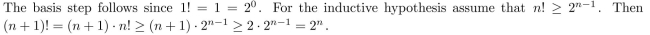
2
Find the sum-of-products expansion of the Boolean function f(x, y, z) that has the value 1 if and only if an odd number of the variables x, y, and z have the value 1.
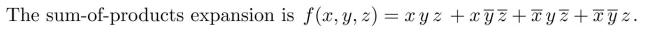
3
A door lock is opened by pushing a sequence of buttons. Each of the three terms in the combination is entered by pushing either one button or two buttons simultaneously. If there are 5 buttons, how many different combinations are there? (Example: 1-3, 2, 2-4 is a valid combination.)

4
Find the prime factorization of 16,575.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
5
(a) Show that the relation 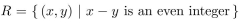 is an equivalence relation on the set of real numbers.
is an equivalence relation on the set of real numbers. 
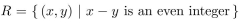 is an equivalence relation on the set of real numbers.
is an equivalence relation on the set of real numbers. 

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
6
Prove or disprove that if A and B are sets then A ∩ (A ∪ B) = A.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
7
Find a spanning tree for the graph 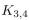 using (a) a depth-first search. (b) a breadth-first search.
using (a) a depth-first search. (b) a breadth-first search.
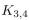 using (a) a depth-first search. (b) a breadth-first search.
using (a) a depth-first search. (b) a breadth-first search.
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
8
(a) How many functions are there from a set with three elements to a set with four elements? (b) How many are one-to-one? (c) How many are onto?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that 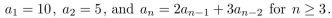 Prove that 5 divides an whenever n is a positive integer.
Prove that 5 divides an whenever n is a positive integer.
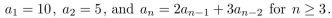 Prove that 5 divides an whenever n is a positive integer.
Prove that 5 divides an whenever n is a positive integer.
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
10
How many positive integers not exceeding 1000 are not divisible by either 8 or 12?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
11
A fair coin is flipped until a tail first appears, at which time no more flips are made.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
12
Find the set recognized by the following deterministic finite-state machine. 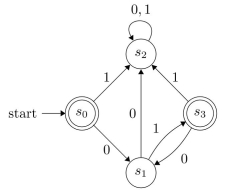


Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
13
How many bit strings of length 10 have at least eight 1's in them?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
14
(a) Prove or disprove: If a ≡ b (mod 5), where a and b are integers, then 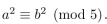 (b) Prove or disprove: If
(b) Prove or disprove: If 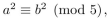 where a and b are integers, then a ≡ b (mod 5).
where a and b are integers, then a ≡ b (mod 5).
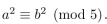 (b) Prove or disprove: If
(b) Prove or disprove: If 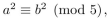 where a and b are integers, then a ≡ b (mod 5).
where a and b are integers, then a ≡ b (mod 5).
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
15
Find a recurrence relation and initial conditions for the number of ways to go up a flight of stairs if stairs can be climbed one, two, or three at a time.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
16
Answer the following questions about the graph 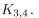 (a) How many vertices and how many edges are in this graph? (b) Is this graph planar? Justify your answer. (c) Does this graph have an Euler circuit? Does it have an Euler path? Give reasons for your answers. (d) What is the chromatic number of this graph?
(a) How many vertices and how many edges are in this graph? (b) Is this graph planar? Justify your answer. (c) Does this graph have an Euler circuit? Does it have an Euler path? Give reasons for your answers. (d) What is the chromatic number of this graph?
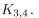 (a) How many vertices and how many edges are in this graph? (b) Is this graph planar? Justify your answer. (c) Does this graph have an Euler circuit? Does it have an Euler path? Give reasons for your answers. (d) What is the chromatic number of this graph?
(a) How many vertices and how many edges are in this graph? (b) Is this graph planar? Justify your answer. (c) Does this graph have an Euler circuit? Does it have an Euler path? Give reasons for your answers. (d) What is the chromatic number of this graph?
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
17
How many bit string of length 10 have at least one 0 in them?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
18
Prove or disprove that 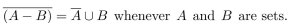
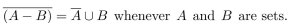

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
19
Prove or disprove that the fourth power of an odd positive integer always leaves a remainder of 1 when divided by 16.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
20
Use mathematical induction to prove that every postage of greater than 5 cents can be formed from 3-cent and 4-cent stamps.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
21
(a) Let 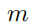 be a positive integer greater than 2 . Show that the relation
be a positive integer greater than 2 . Show that the relation 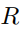 consisting of those ordered pairs of integers (a, b) with
consisting of those ordered pairs of integers (a, b) with 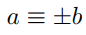 (mod m) is an equivalence relation.
(mod m) is an equivalence relation.
(b) Describe the equivalence classes of this relation where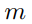 =4 .
=4 .
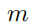 be a positive integer greater than 2 . Show that the relation
be a positive integer greater than 2 . Show that the relation 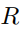 consisting of those ordered pairs of integers (a, b) with
consisting of those ordered pairs of integers (a, b) with 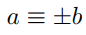 (mod m) is an equivalence relation.
(mod m) is an equivalence relation.(b) Describe the equivalence classes of this relation where
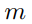 =4 .
=4 .
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
22
How many nonisomorphic unrooted trees are there with four vertices? Draw these trees.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
23
(a) Describe the bit strings that are in the regular set represented by 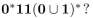 (b) Construct a nondeterministic finite-state automaton that recognizes this set.
(b) Construct a nondeterministic finite-state automaton that recognizes this set.
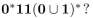 (b) Construct a nondeterministic finite-state automaton that recognizes this set.
(b) Construct a nondeterministic finite-state automaton that recognizes this set.
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
24
Find the sum-of-products expansion for the Boolean function 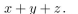
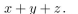

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
25
(a) Does the graph 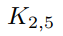 have an Euler circuit? If not, does it have an Euler path?
have an Euler circuit? If not, does it have an Euler path?
(b) Does the graph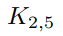 have a Hamilton path?
have a Hamilton path?
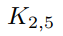 have an Euler circuit? If not, does it have an Euler path?
have an Euler circuit? If not, does it have an Euler path?(b) Does the graph
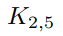 have a Hamilton path?
have a Hamilton path?
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
26
(a) How many functions are there from a set with four elements to a set with three elements? (b) How many of these functions are one-to-one? (c) How many are onto?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
27
A thumb tack is tossed until it first lands with its point down, at which time no more tosses are made. On each toss, the probability of the tack's landing point down is 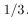 (a) What is the probability that exactly five tosses are made? (b) What is the expected number of tosses?
(a) What is the probability that exactly five tosses are made? (b) What is the expected number of tosses?
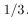 (a) What is the probability that exactly five tosses are made? (b) What is the expected number of tosses?
(a) What is the probability that exactly five tosses are made? (b) What is the expected number of tosses?
Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
28
How many symmetric relations are there on a set with eight elements?

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck
29
Construct a binary search tree from the words of the sentence This is your discrete mathematics final, using alphabetical order, inserting words in the order they appear in the sentence.

Unlock Deck
Unlock for access to all 29 flashcards in this deck.
Unlock Deck
k this deck


