Deck 8: A: Advanced Counting Techniques
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 8: A: Advanced Counting Techniques
1
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.
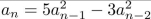
constant coefficients.
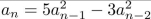
No
2
Find the solution of the recurrence relation an = 3an−1 with a0 = 2.

3
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.

constant coefficients.

Yes
4
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.
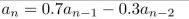
constant coefficients.
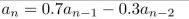

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.
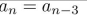
constant coefficients.
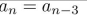

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
describe each sequence recursively. Include initial conditions and assume that the sequences begin
with a1.
an = the number of bit strings of length n that begin with 1
with a1.
an = the number of bit strings of length n that begin with 1

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.
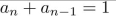
constant coefficients.
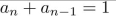

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
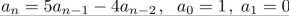
pattern formed by the terms.
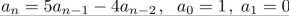

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
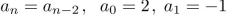
pattern formed by the terms.
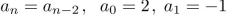

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
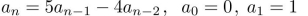
pattern formed by the terms.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
A vending machine dispensing books of stamps accepts only $1 coins, $1 bills, and $2 bills. Let an denote

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
describe each sequence recursively. Include initial conditions and assume that the sequences begin
with a1.
an = the number of ways to go down an n-step staircase if you go down 1, 2, or 3 steps at a time
with a1.
an = the number of ways to go down an n-step staircase if you go down 1, 2, or 3 steps at a time

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
describe each sequence recursively. Include initial conditions and assume that the sequences begin
with a1.
an = the number of bit strings of length n that contain a pair of consecutive 0's
with a1.
an = the number of bit strings of length n that contain a pair of consecutive 0's

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
determine whether the recurrence relation is a linear homogeneous recurrence relation with
constant coefficients.
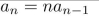
constant coefficients.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.

pattern formed by the terms.


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
describe each sequence recursively. Include initial conditions and assume that the sequences begin
with a1.
an = the number of bit strings of length n with an even number of 0's
with a1.
an = the number of bit strings of length n with an even number of 0's

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
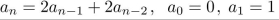
pattern formed by the terms.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.

pattern formed by the terms.


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
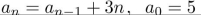
pattern formed by the terms.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
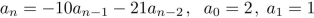
pattern formed by the terms.
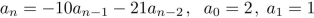

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
What form does a particular solution of the linear nonhomogeneous recurrence relation 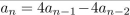 +
+ 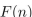 have when
have when 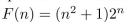 ?
?
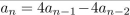 +
+ 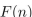 have when
have when 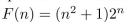 ?
?
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
Assume that the characteristic equation for a homogeneous linear recurrence relation with constant coeffi- cients is 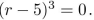 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
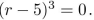 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the recurrence relation 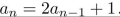 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
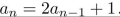 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
Suppose 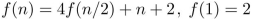 . Find https://storage.examlex.com/TB6843/
. Find https://storage.examlex.com/TB6843/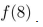 .
.
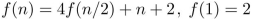 . Find https://storage.examlex.com/TB6843/
. Find https://storage.examlex.com/TB6843/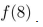 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
The solutions to 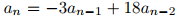 have the form
have the form 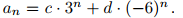 Which of the following are solutions to the given recurrence relation?
Which of the following are solutions to the given recurrence relation?
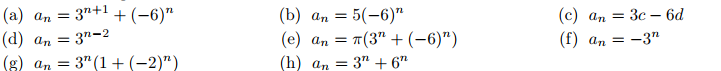
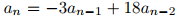 have the form
have the form 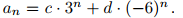 Which of the following are solutions to the given recurrence relation?
Which of the following are solutions to the given recurrence relation?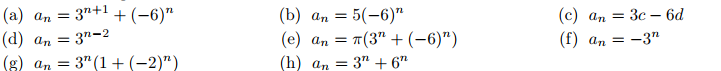

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose 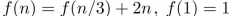 . Find
. Find 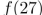 .
.
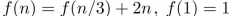 . Find
. Find 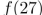 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose https://storage.examlex.com/TB34225555/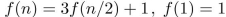 . Find https://storage.examlex.com/TB34225555/
. Find https://storage.examlex.com/TB34225555/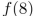 .
.
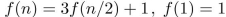 . Find https://storage.examlex.com/TB34225555/
. Find https://storage.examlex.com/TB34225555/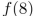 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
The Catalan numbers Cn count the number of strings of n +’s and n −’s with the following property: as
each string is read from left to right, the number of +’s encountered is always at least as large as the number
of −’s.
(a) Verify this by listing these strings of lengths 2, 4, and 6 and showing that there are C1 , C2 , and C3 of
these, respectively.
(b) Explain how counting these strings is the same as counting the number of ways to correctly parenthesize
strings of variables
each string is read from left to right, the number of +’s encountered is always at least as large as the number
of −’s.
(a) Verify this by listing these strings of lengths 2, 4, and 6 and showing that there are C1 , C2 , and C3 of
these, respectively.
(b) Explain how counting these strings is the same as counting the number of ways to correctly parenthesize
strings of variables

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose 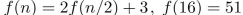 . Find
. Find 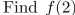 .
.
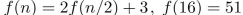 . Find
. Find 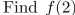 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
What form does a particular solution of the linear nonhomogeneous recurrence relation 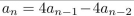 +
+ 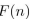 have when
have when 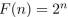 ?
?
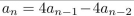 +
+ 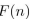 have when
have when 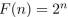 ?
?
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Assume that the characteristic equation for a homogeneous linear recurrence relation with constant coeffi- cients is 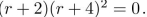 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
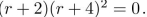 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Suppose 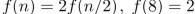 . Find
. Find 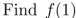 .
.
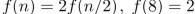 . Find
. Find 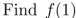 .
.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the recurrence relation 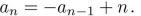 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
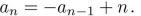 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the recurrence relation 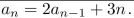 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation.
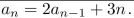 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the recurrence relation 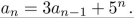 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
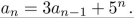 (a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
(a) Write the associated homogeneous recurrence relation. (b) Find the general solution to the associated homogeneous recurrence relation. (c) Find a particular solution to the given recurrence relation. (d) Write the general solution to the given recurrence relation. (e) Find the particular solution to the given recurrence relation when a0 = 1.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
What form does a particular solution of the linear nonhomogeneous recurrence relation 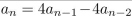 +
+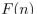 have when
have when 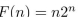 ?
?
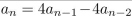 +
+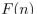 have when
have when 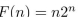 ?
?
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
What form does a particular solution of the linear nonhomogeneous recurrence relation 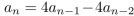 +
+ 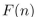 have when
have when 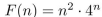
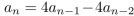 +
+ 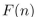 have when
have when 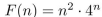

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
Assume that the characteristic equation for a homogeneous linear recurrence relation with constant coeffi- cients is 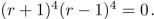 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
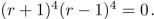 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
solve the recurrence relation either by using the characteristic equation or by discovering a
pattern formed by the terms.
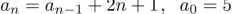
pattern formed by the terms.
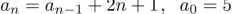

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Assume that the characteristic equation for a homogeneous linear recurrence relation with constant coeffi- cients is 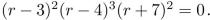 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
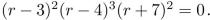 Describe the form for the general solution to the recurrence relation.
Describe the form for the general solution to the recurrence relation.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
find the coefficient of x8 in the power series of each of the function.
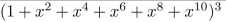
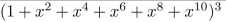

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
write the first seven terms of the sequence determined by the generating function.
5
5

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
write the first seven terms of the sequence determined by the generating function.
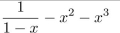
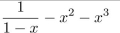

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
find the coefficient of x8 in the power series of each of the function.
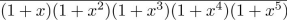
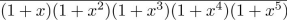

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
write the first seven terms of the sequence determined by the generating function.
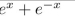
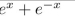

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
write the first seven terms of the sequence determined by the generating function.
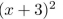
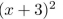

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
find the coefficient of x8 in the power series of each of the function.
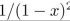
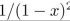

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Use generating functions to solve 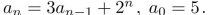
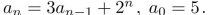

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Use generating functions to solve 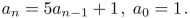
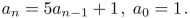

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
find the coefficient of x8 in the power series of each of the function.
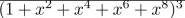
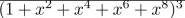

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
find the coefficient of x8 in the power series of each of the function.
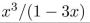
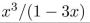

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
write the first seven terms of the sequence determined by the generating function.
cos x
cos x

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
write the first seven terms of the sequence determined by the generating function.
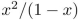
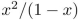

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
write the first seven terms of the sequence determined by the generating function.
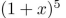
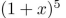

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
find the coefficient of x8 in the power series of each of the function.
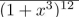
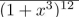

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
write the first seven terms of the sequence determined by the generating function.
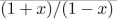
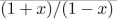

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
write the first seven terms of the sequence determined by the generating function.
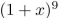
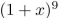

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
find the coefficient of x8 in the power series of each of the function.
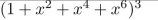
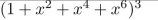

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
write the first seven terms of the sequence determined by the generating function.
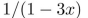
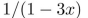

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
find the coefficient of x8 in the power series of each of the function.
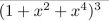
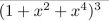

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
find a closed form for the generating function for the sequence.
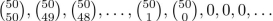
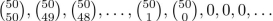

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
find a closed form for the generating function for the sequence.
2, 4, 6, 8, 10, 12, . . .
2, 4, 6, 8, 10, 12, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
Set up a generating function and use it to find the number of ways in which eleven identical coins can be put in three distinct envelopes if each envelope has at least two coins in it.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
find a closed form for the generating function for the sequence.
2, 0, 0, 2, 0, 0, 2, 0, 0, 2, . . .
2, 0, 0, 2, 0, 0, 2, 0, 0, 2, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
find the coefficient of x8 in the power series of each of the function.
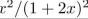
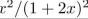

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
find a closed form for the generating function for the sequence.
1, 0, −1, 0, 1, 0, −1, 0, 1, 0, −1, . . .
1, 0, −1, 0, 1, 0, −1, 0, 1, 0, −1, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
Set up a generating function and use it to find the number of ways in which eleven identical coins can be put in three distinct envelopes if no envelope is empty.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
Set up a generating function and use it to find the number of ways in which eleven identical coins can be put in three distinct envelopes if each envelope has at least two but no more than five coins in it.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Set up a generating function and use it to find the number of ways in which eleven identical coins can be put in three distinct envelopes if each envelope has an even number of coins in it.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
find the coefficient of x8 in the power series of each of the function.
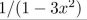
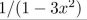

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
find a closed form for the generating function for the sequence.
0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, . . .
0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
find a closed form for the generating function for the sequence.
1, −1, 12!, −3!1 , 14!, − 15!, . . .
1, −1, 12!, −3!1 , 14!, − 15!, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
find a closed form for the generating function for the sequence.
4, 8, 16, 32, 64, . . .
4, 8, 16, 32, 64, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
find a closed form for the generating function for the sequence.
1, −1, 1, −1, 1, −1, 1, −1, . . .
1, −1, 1, −1, 1, −1, 1, −1, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
find a closed form for the generating function for the sequence.
1, 12!, 14!, 16!, 18! . . .
1, 12!, 14!, 16!, 18! . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
find a closed form for the generating function for the sequence.
2, 3, 4, 5, 6, 7, . . .
2, 3, 4, 5, 6, 7, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
find a closed form for the generating function for the sequence.
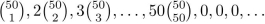
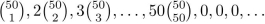

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
find a closed form for the generating function for the sequence.
0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1 . . .
0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1 . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
Set up a generating function and use it to find the number of ways in which eleven identical coins can be put in three distinct envelopes if each envelope has most six coins in it.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
find a closed form for the generating function for the sequence.
1, 0, 1, 0, 1, 0, 1, 0, . . .
1, 0, 1, 0, 1, 0, 1, 0, . . .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


