Deck 12: Fractal Geometry: the Kinky Nature of Nature
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/39
Play
Full screen (f)
Deck 12: Fractal Geometry: the Kinky Nature of Nature
1
Refer to the information from table shown above ; what is the total length of the darkened boundary of the Sierpinski gasket created if the Step process were to continue indefinitely?
Infinite length
2
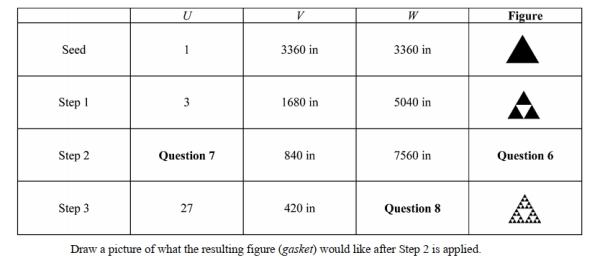
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose perimeter is 3360
in. The table below gives the following information where U is the number of darkened triangles at a particular step, V is the perimeter of each darkened triangle, and W is the total length of the darkened boundary of the figure (gasket) obtained in a particular step.
in. The table below gives the following information where U is the number of darkened triangles at a particular step, V is the perimeter of each darkened triangle, and W is the total length of the darkened boundary of the figure (gasket) obtained in a particular step.

6.


3
Refer to the table shown above ; how many triangles will be added in Step 3?
48
4
The following is called the Chaos Game. Start with a square ABCD in which A is located at (0,0), B is located at (27,0), C is located at (27,27) , and D is located at (0,27) . Then, roll a fair die. We will say that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3 , and D is the winner if we roll a 4 . If we roll a 5 or 6 , we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
- Start: Roll the die. Mark the winning vertex and call it P1 .
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .
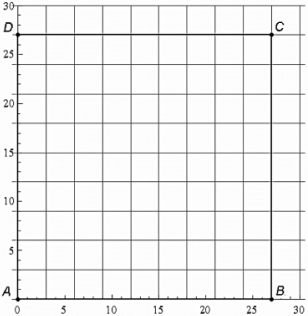
What would be the sequence (1,2,3) was rolled?
- Start: Roll the die. Mark the winning vertex and call it P1 .
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .

What would be the sequence (1,2,3) was rolled?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
5
You plan on constructing a Koch snowflake by starting with a seed triangle whose perimeter is X. The table below gives the following information where M is the number of sides at a particular step, L is the length of each side, and P is the total perimeter of the figure. 


Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
6
To answer the following question, refer to the Mandelbrot replacement process described by:
Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence: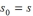
Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: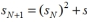
If the seed is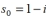 , then find the term
, then find the term 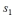
Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence:
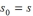
Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
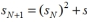
If the seed is
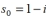 , then find the term
, then find the term 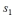

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
7

Refer to the table shown above ; how many sides does the figure have in Step 2?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
8

Refer to the information from table shown above ; what is the total length of the darkened boundary of the resulting figure (Sierpinski gasket) in Step 3?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
9

Refer to the information from table shown above ; what is the perimeter of the Koch snowflake created if the
Step process were to continue indefinitely?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
10
The following is called the Chaos Game. Start with a square ABCD in which A is located at (0,0), B is located at (27,0), C is located at (27,27) , and D is located at (0,27) . Then, roll a fair die. We will say that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is the winner if we roll a 4 . If we roll a 5 or 6 , we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
- Start: Roll the die. Mark the winning vertex and call it P1.
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .
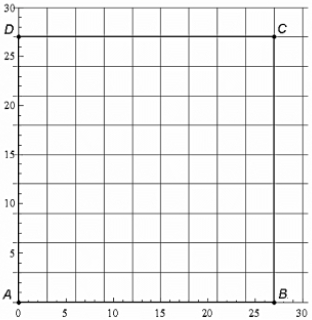
What would be the resulting coordinates of P3 if the sequence of (4,1,4) was rolled?
- Start: Roll the die. Mark the winning vertex and call it P1.
- Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next winning vertex. Mark this point and call it P2 .
- Steps 2,3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way from the last position to the winning vertex.
The grid below show the square ABCD .

What would be the resulting coordinates of P3 if the sequence of (4,1,4) was rolled?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
11

Refer to the table shown above ; what is the total area T in Step 3?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
12

Refer to the table shown above ; what is the area of each added triangle in Step 2?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
13

Refer to the table shown above ; what is the total area of the figure after Step 3?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
14

Refer to the table shown above ; what is the original perimeter X of the seed triangle

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
15

Refer to the table shown above; how many darkened triangles are there in Step 2?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
16

Refer to the information in the table above ; what is the area of the Koch snowflake created if the Step
process were to continue indefinitely?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
17
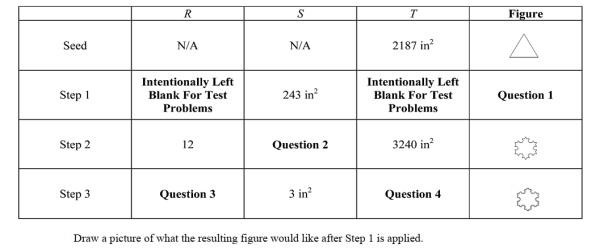
You plan on constructing a Koch snowflake by starting with a seed triangle whose area is 2187 in2. The table below gives the following information where R is the number of triangles added at a particular step, S is the area of each added triangle, and T is the total area of the newly created figure. 


Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
18
To answer the following question, refer to the Mandelbrot replacement process described by:
- Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed as the initial term of the sequence: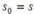
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: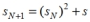
If the seed is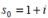 , then find the term https://storage.examlex.com/TB34225555/
, then find the term https://storage.examlex.com/TB34225555/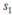 .
.
- Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed as the initial term of the sequence:
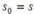
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
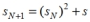
If the seed is
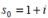 , then find the term https://storage.examlex.com/TB34225555/
, then find the term https://storage.examlex.com/TB34225555/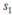 .
.
Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
19
Refer to the information shown above ; what is the total area of the Sierpinski gasket created if the Step process were to continue indefinitely?

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
20
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose area is 2304 in2. The table below gives the following information where R is the number of triangles removed at a particular step, S is the area of each removed triangle, and T is the total area of the newly created figure. 


Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
21
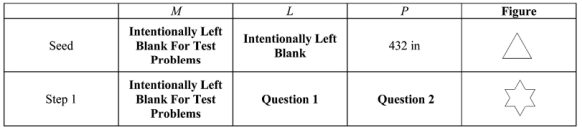
Refer to the information from table shown above ; what is the perimeter of the Koch snowflake created if the Step process were to continue indefinitely?
A) 810 in
B) 2073 in
C) 4651 in
D) Infinite perimeter.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
22
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose perimeter is X. The table below gives the following information where U is the number of darkened triangles at a particular step, V is the perimeter of each darkened triangle, and W is the length of the darkened boundary of the figure (gasket) obtained in a particular step. 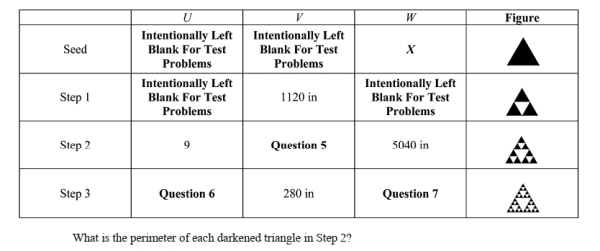
A) 440 in
B) 560 in
C) 760 in
D) 840 in
E) None of the above.

A) 440 in
B) 560 in
C) 760 in
D) 840 in
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
23
Which of the following is an example of fractal behavior in nature?
A) a digital photograph
B) a skyscraper
C) a lightening bolt
D) All of the above.
E) None of the above.
A) a digital photograph
B) a skyscraper
C) a lightening bolt
D) All of the above.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
24
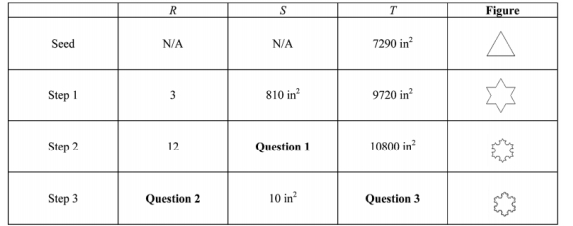
You plan on constructing a Sierpinski gasket by starting with a seed triangle whose area is 6720 in2. The table below gives the following information where R is the number of triangles removed at a
Particular step, S is the area of each removed triangle, and T is the total area of the newly created figure.
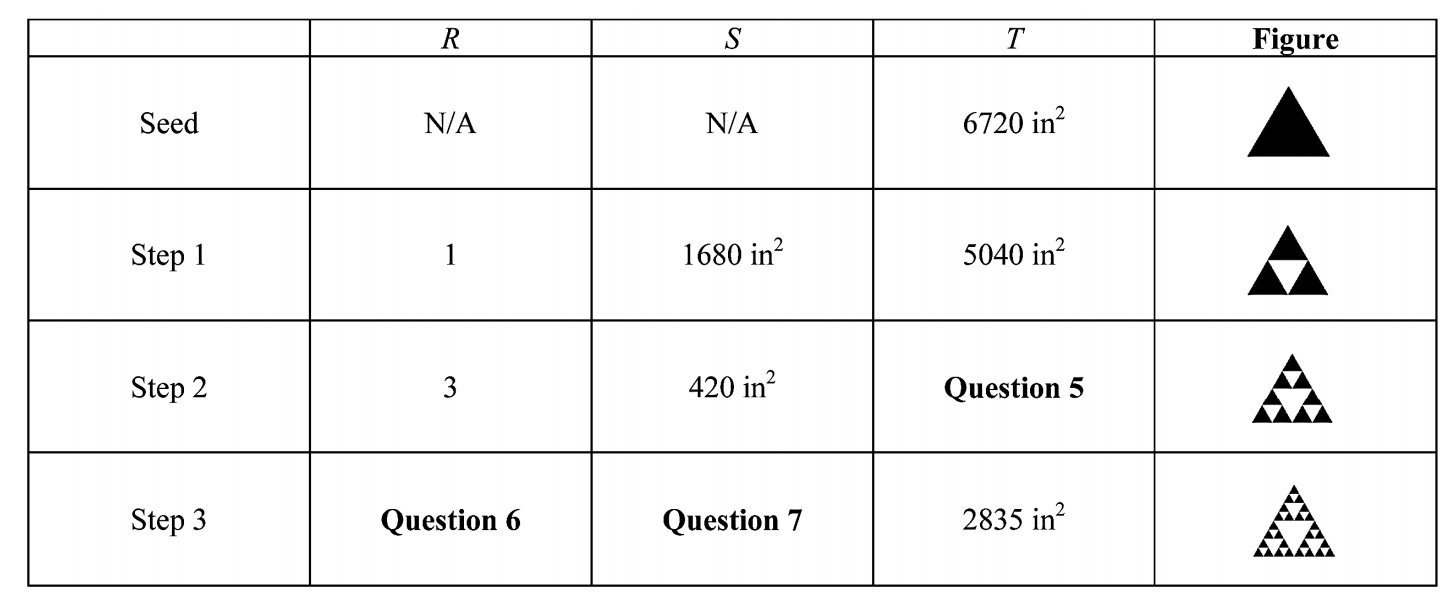
What is the total area of the figure after step 2 ?
A) 2160 in2
B) 3780 in2
C) 4310in2
D) 6300in2
E) None of the above.
Particular step, S is the area of each removed triangle, and T is the total area of the newly created figure.

What is the total area of the figure after step 2 ?
A) 2160 in2
B) 3780 in2
C) 4310in2
D) 6300in2
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
25
To answer the following question, refer to the Mandelbrot replacement process described by:
- Start: Choose an arbitrary complex number s, called the seed of the Mandelbrot sequence. Set the seed s to be the initial term of the sequence: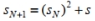
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: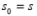
Which of the statements below is correct?
A) The seed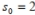 initiates a Mandelbrot sequence which is escaping.
initiates a Mandelbrot sequence which is escaping.
B) The seed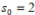 initiates a Mandelbrot sequence which is periodic.
initiates a Mandelbrot sequence which is periodic.
C) The seed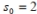 initiates a Mandelbrot sequence which is attracted.
initiates a Mandelbrot sequence which is attracted.
D) All of the above.
E) None of the above.
- Start: Choose an arbitrary complex number s, called the seed of the Mandelbrot sequence. Set the seed s to be the initial term of the sequence:
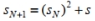
- Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
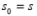
Which of the statements below is correct?
A) The seed
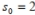 initiates a Mandelbrot sequence which is escaping.
initiates a Mandelbrot sequence which is escaping.B) The seed
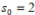 initiates a Mandelbrot sequence which is periodic.
initiates a Mandelbrot sequence which is periodic.C) The seed
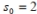 initiates a Mandelbrot sequence which is attracted.
initiates a Mandelbrot sequence which is attracted.D) All of the above.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
26
Refer to the table shown above ; how many triangles will be added in Step 3?
A) 18
B) 24
C) 36
D) 48
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
27

Refer to the table shown above ; what is the total perimeter length in Step 1?
(a) 324 in
(b) 576 in
(c) 648 in
(d) 1296 in
(e) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
28
The following is called the Chaos Game. Start with a square ABCD in which A is located at (0, 0), B is
located at (27, 0), C is located at (27, 27), and D is located at (0, 27). Then, roll a fair die. We will say
that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is
the winner if we roll a 4. If we roll a 5 or 6, we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
Start: Roll the die. Mark the winning vertex and call it P1.
Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next
winning vertex. Mark this point and call it P2.
Steps 2, 3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way
from the last position to the winning vertex.
The grid below show the square ABCD.
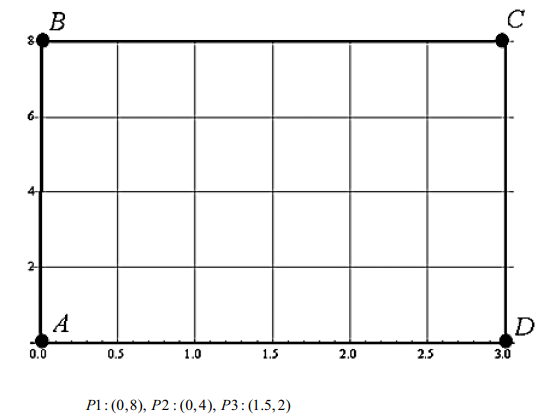
A) (2,1,4)
B) (1,3,3)
C) (2,1,3)
D) (2,3,1)
E) None of the above.
located at (27, 0), C is located at (27, 27), and D is located at (0, 27). Then, roll a fair die. We will say
that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is
the winner if we roll a 4. If we roll a 5 or 6, we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
Start: Roll the die. Mark the winning vertex and call it P1.
Step 1: Roll the die again. From P1 move two-thirds of the way straight towards the next
winning vertex. Mark this point and call it P2.
Steps 2, 3, etc.: Continue rolling the die, each time moving to a point two-thirds of the way
from the last position to the winning vertex.
The grid below show the square ABCD.

A) (2,1,4)
B) (1,3,3)
C) (2,1,3)
D) (2,3,1)
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
29

Refer to the table shown above ; what is the area of each of the triangles removed during Step 3 ?
A) 90 in2
B) 125 in2
C) 240 in2
D) 380 in2
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
30
The following is called the Chaos Game. Start with rectangle ABCD in which A is located at (0, 0), B
is located at (0, 8), C is located at (3, 8), and D is located at (3, 0). Then, roll a fair die. We will say
that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is
the winner if we roll a 4. If we roll a 5 or 6, we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
Start: Roll the die. Mark the winning vertex and call it P1.
Step 1: Roll the die again. From P1 move one-half of the way straight toward the next
winning vertex. Mark this point and call it P2. Steps 2, 3, etc.: Continue rolling the die, each time moving to a point one-half of the way
from the last position to the winning vertex.
The grid below shows rectangle ABCD.
https://storage.examlex.com/TB6029/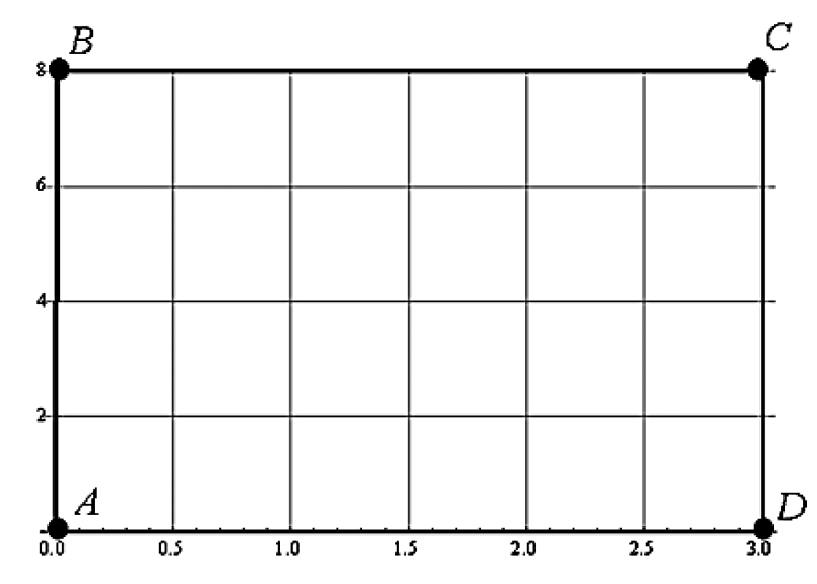 .
.
What sequence of rolls would produce the following sequence of marked points?
P1: (0,8), P2 : (1.5,8), P3 : (0.75, 4)
(a) (2,3,1)
(b) (1,4,2)
(c) (2,1,4)
(d) (2,4,3)
(e) None of the above.
is located at (0, 8), C is located at (3, 8), and D is located at (3, 0). Then, roll a fair die. We will say
that A is the winner if we roll a 1, B is the winner if we roll a 2, C is the winner if we roll a 3, and D is
the winner if we roll a 4. If we roll a 5 or 6, we disregard the roll and roll again. Each roll of the die generates a point inside or on the boundary of the square according to the following rules.
Start: Roll the die. Mark the winning vertex and call it P1.
Step 1: Roll the die again. From P1 move one-half of the way straight toward the next
winning vertex. Mark this point and call it P2. Steps 2, 3, etc.: Continue rolling the die, each time moving to a point one-half of the way
from the last position to the winning vertex.
The grid below shows rectangle ABCD.
https://storage.examlex.com/TB6029/
 .
.What sequence of rolls would produce the following sequence of marked points?
P1: (0,8), P2 : (1.5,8), P3 : (0.75, 4)
(a) (2,3,1)
(b) (1,4,2)
(c) (2,1,4)
(d) (2,4,3)
(e) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
31
You plan on constructing a Koch snowflake by starting with a seed triangle whose area is 7290 in2. The table below gives the following information where R is the number of triangles added at a particular step, S is the area of each added triangle, and T is the total area of the newly created figure. 
What is the area of each added triangle in Step 2 ?
A) 45 in2
B) 90 in2
C) 105 in2
D) 162 in2
E) None of the above.

What is the area of each added triangle in Step 2 ?
A) 45 in2
B) 90 in2
C) 105 in2
D) 162 in2
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
32
You plan on constructing a Koch snowflake by starting with a seed triangle whose perimeter is 432 in. The table below gives the following information where M is the number of sides at a particular step, L
Is the length of each side, and P is the total perimeter of the figure. What is the length of each side of the figure in Step 1?

A) 36 in
B) 48 in
C) 72 in
D) 144 in
E) None of the above.
Is the length of each side, and P is the total perimeter of the figure. What is the length of each side of the figure in Step 1?

A) 36 in
B) 48 in
C) 72 in
D) 144 in
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
33

Refer to the table shown above ; how many triangles are removed during Step 3?
A) 9
B) 18
C) 27
D) 36
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
34

Refer to the information in the table shown above ; how many darkened triangles are there in Step 3?
A) 18
B) 27
C) 36
D) 45
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
35

Refer to the information from the table shown above ; what is the total length of the darkened boundary of the resulting figure (gasket) in Step 3?
A) 5670 in
B) 6720 in
C) 7560 in
D) 8960 in
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
36

Refer to the table shown above ; what is the total area of the figure after Step 3?
A) 11280 in2
B) 12630 in2
C) 14320 in2
D) 16440 in2
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following is an example of fractal behavior in nature?
A) coastline
B) mountain ridge
C) head of cauliflower
D) All of the above.
E) None of the above.
A) coastline
B) mountain ridge
C) head of cauliflower
D) All of the above.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
38
To answer the following question, refer to the Mandelbrot replacement process described by:
a. Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence: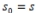
b. Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed: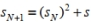
Which of the statements below is correct?
A) The seed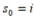 initiates a Mandelbrot sequence which is escaping.
initiates a Mandelbrot sequence which is escaping.
B) The seed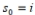 initiates a Mandelbrot sequence which is periodic.
initiates a Mandelbrot sequence which is periodic.
C) The seed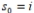 initiates a Mandelbrot sequence which is attracted.
initiates a Mandelbrot sequence which is attracted.
D) All of the above.
E) None of the above.
a. Start: Choose an arbitrary complex number s , called the seed of the Mandelbrot sequence. Set the seed s as the initial term of the sequence:
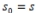
b. Recursive Procedure: To find the next term in the sequence, square the preceding term and add the seed:
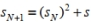
Which of the statements below is correct?
A) The seed
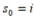 initiates a Mandelbrot sequence which is escaping.
initiates a Mandelbrot sequence which is escaping.B) The seed
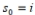 initiates a Mandelbrot sequence which is periodic.
initiates a Mandelbrot sequence which is periodic.C) The seed
 initiates a Mandelbrot sequence which is attracted.
initiates a Mandelbrot sequence which is attracted.D) All of the above.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck
39
Two Koch snowflakes are shown below. One was created by starting with a seed triangle whose perimeter was 10 units while the other was created by starting with a seed triangle whose perimeter was 30 units. Assuming that the iterative process continues indefinitely, which of the snowflakes below has the larger perimeter? 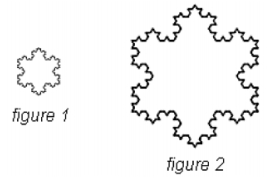
A) figure 1
B) figure 2
C) figures 1 and 2 both have infinite perimeter.
D) Insufficient information.
E) None of the above.

A) figure 1
B) figure 2
C) figures 1 and 2 both have infinite perimeter.
D) Insufficient information.
E) None of the above.

Unlock Deck
Unlock for access to all 39 flashcards in this deck.
Unlock Deck
k this deck


