Deck 10: First-Order Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/90
Play
Full screen (f)
Deck 10: First-Order Differential Equations
1
Match the differential equation with the appropriate slope field.
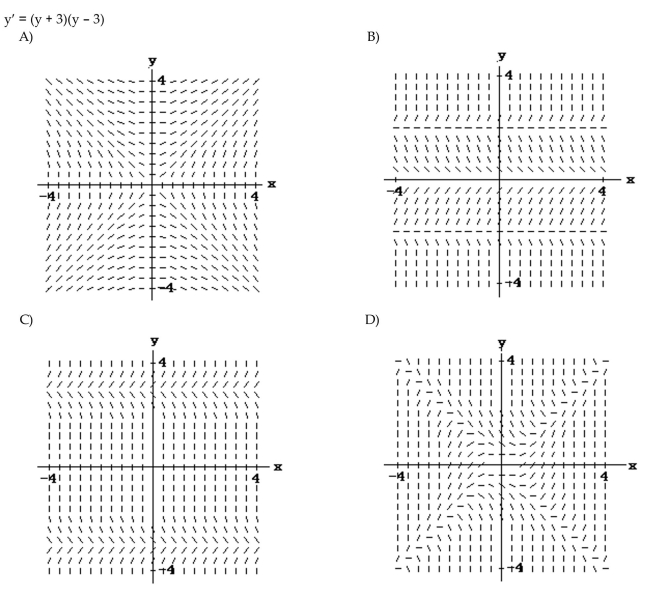

C
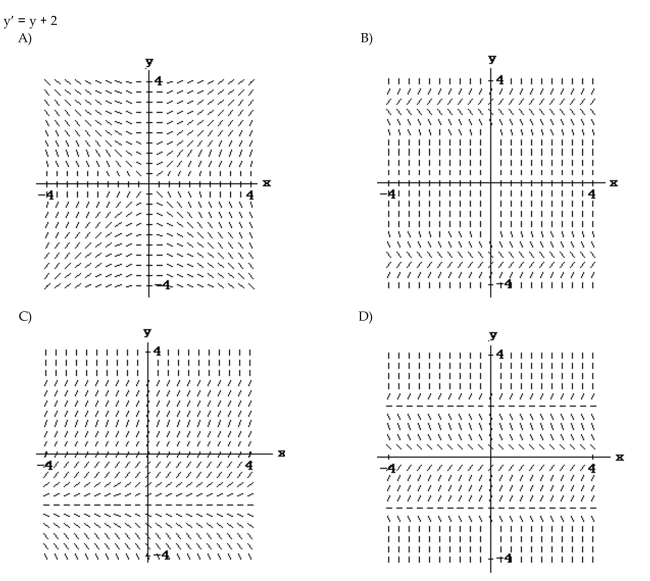
2
Match the differential equation with the appropriate slope field.
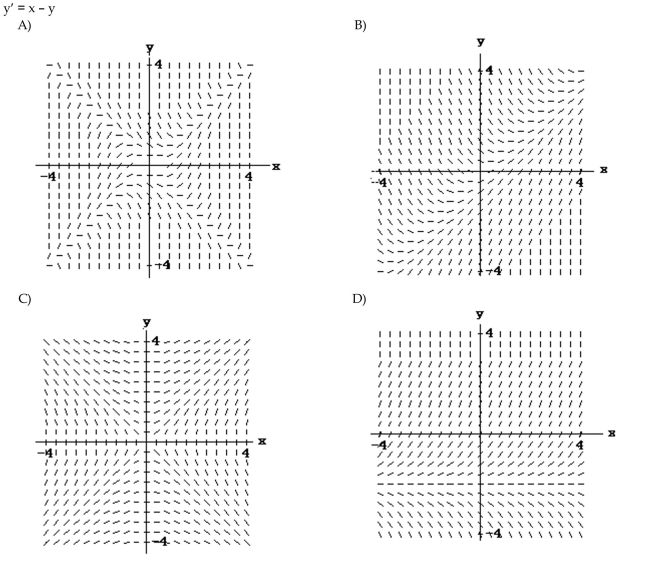

B
3
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
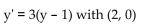
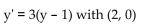
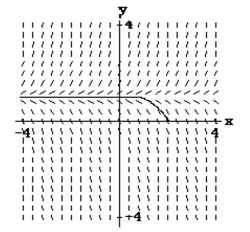
4
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
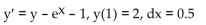
A) y1 = 1.6409, y2 = 0.2704, y3 = -5.3889
B) y1 = 2.1409, y2 = 1.5704, y3 = -5.0389
C) y1 = 0.6409, y2 = -2.3296, y3 = -6.0889
D) y1 = 1.1409, y2 = -1.0296, y3 = -5.7389
increment size. Round your results to four decimal places.
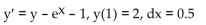
A) y1 = 1.6409, y2 = 0.2704, y3 = -5.3889
B) y1 = 2.1409, y2 = 1.5704, y3 = -5.0389
C) y1 = 0.6409, y2 = -2.3296, y3 = -6.0889
D) y1 = 1.1409, y2 = -1.0296, y3 = -5.7389

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
5
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
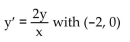
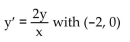

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
6
Match the differential equation with the appropriate slope field.
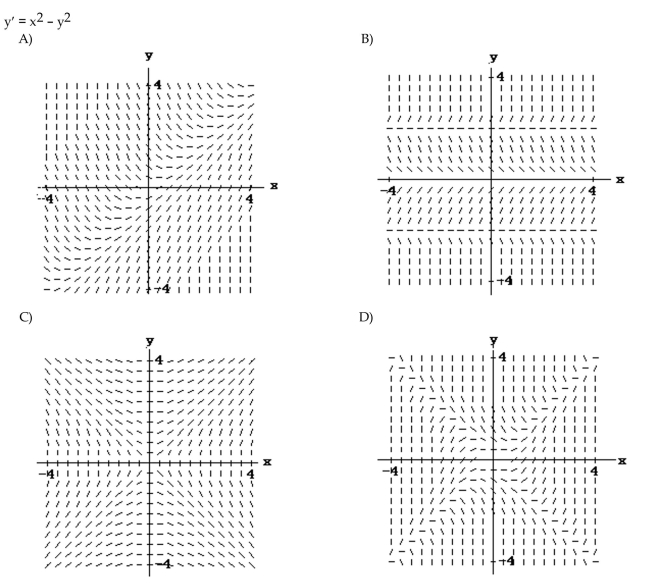


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
7
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
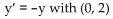
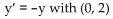

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
8
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
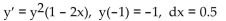
A) y1 = 0.4, y2 = 0.63, y3 = 0.7472
B) y1 = 0.7, y2 = 0.99, y3 = 1.9136
C) y1 = 0.5, y2 = 0.75, y3 = 1.03125
D) y1 = 0.7, y2 = 0.99, y3 = 1.2656
increment size. Round your results to four decimal places.
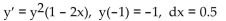
A) y1 = 0.4, y2 = 0.63, y3 = 0.7472
B) y1 = 0.7, y2 = 0.99, y3 = 1.9136
C) y1 = 0.5, y2 = 0.75, y3 = 1.03125
D) y1 = 0.7, y2 = 0.99, y3 = 1.2656

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
9
Solve. Round your results to four decimal places.
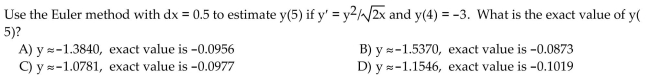
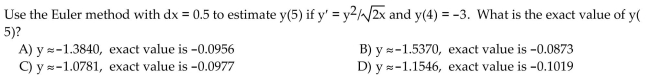

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
10
Solve. Round your results to four decimal places.
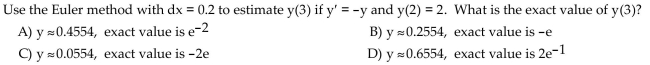
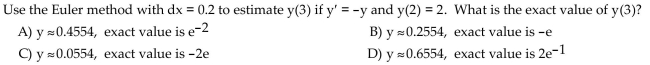

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
11
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
y = 2xy - 2y, y(2) = 3, dx = 0.2
A) y1 = 0.9000, y2 = 6.2160, y3 = 15.9130
B) y1 = 2.7000, y2 = 3.8850, y3 = 29.8368
C) y1 = 4.5000, y2 = 6.9930, y3 = 19.8912
D) y1 = 4.2000, y2 = 6.2160, y3 = 9.6970
increment size. Round your results to four decimal places.
y = 2xy - 2y, y(2) = 3, dx = 0.2
A) y1 = 0.9000, y2 = 6.2160, y3 = 15.9130
B) y1 = 2.7000, y2 = 3.8850, y3 = 29.8368
C) y1 = 4.5000, y2 = 6.9930, y3 = 19.8912
D) y1 = 4.2000, y2 = 6.2160, y3 = 9.6970

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
12
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
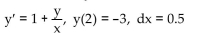
A) y1 = -4.8750, y2 = -4.0800, y3 = -4.1600
B) y1 = -3.2500, y2 = -3.4000, y3 = -3.4667
C) y1 = -6.5000, y2 = -6.8000, y3 = -13.8667
D) y1 = -6.5000, y2 = -5.1000, y3 = -6.9333
increment size. Round your results to four decimal places.
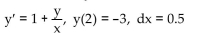
A) y1 = -4.8750, y2 = -4.0800, y3 = -4.1600
B) y1 = -3.2500, y2 = -3.4000, y3 = -3.4667
C) y1 = -6.5000, y2 = -6.8000, y3 = -13.8667
D) y1 = -6.5000, y2 = -5.1000, y3 = -6.9333

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
13
Match the differential equation with the appropriate slope field.
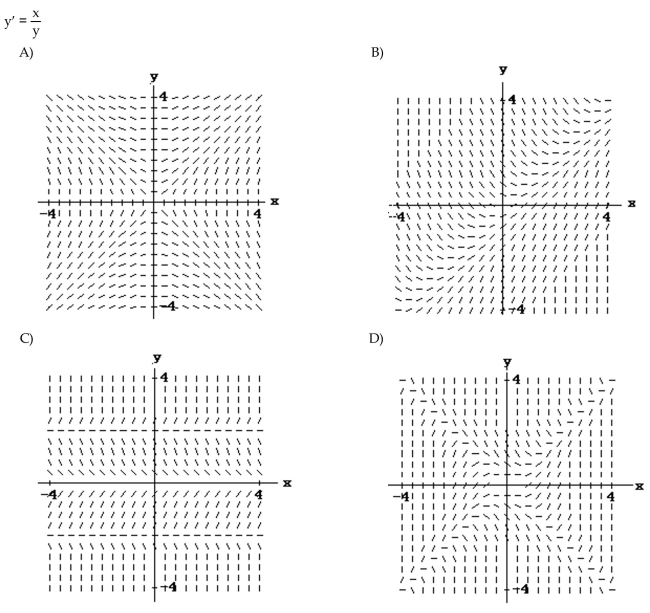


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
14
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
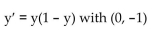
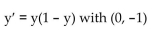

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
15
Solve. Round your results to four decimal places.
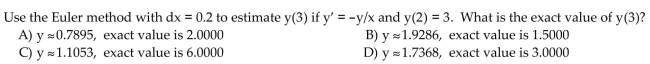
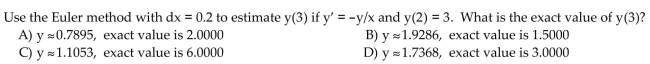

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
16
Match the differential equation with the appropriate slope field.
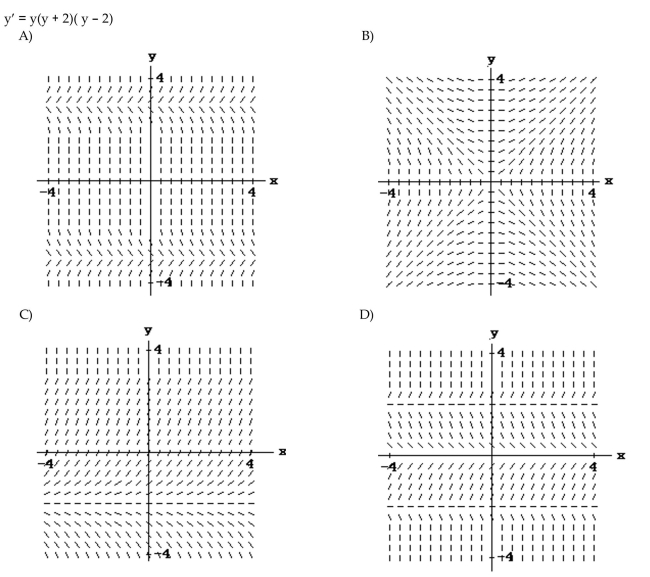


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
17
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
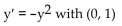
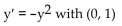

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
18
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
y = -x(1 - y), y(2) = 3, dx = 0.2
A) y1 = 3.8000, y2 = 5.0320, y3 = 6.9674
B) y1 = 7.0000, y2 = 50.3200, y3 = 69.6736
C) y1 = 0.7000, y2 = 2.5160, y3 = 3.4837
D) y1 = 2.8000, y2 = 10.0640, y3 = 13.9347
increment size. Round your results to four decimal places.
y = -x(1 - y), y(2) = 3, dx = 0.2
A) y1 = 3.8000, y2 = 5.0320, y3 = 6.9674
B) y1 = 7.0000, y2 = 50.3200, y3 = 69.6736
C) y1 = 0.7000, y2 = 2.5160, y3 = 3.4837
D) y1 = 2.8000, y2 = 10.0640, y3 = 13.9347

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
19
Use Euler's method to calculate the first three approximations to the given initial value problem for the specified
increment size. Round your results to four decimal places.
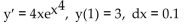
A) y1 = 3.2699, y2 = 5.1723, y3 = 8.9899
B) y1 = 4.0873, y2 = 5.9897, y3 = 9.8074
C) y1 = 3.6786, y2 = 5.5810, y3 = 9.3986
D) y1 = 4.4960, y2 = 6.3985, y3 = 10.2161
increment size. Round your results to four decimal places.
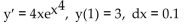
A) y1 = 3.2699, y2 = 5.1723, y3 = 8.9899
B) y1 = 4.0873, y2 = 5.9897, y3 = 9.8074
C) y1 = 3.6786, y2 = 5.5810, y3 = 9.3986
D) y1 = 4.4960, y2 = 6.3985, y3 = 10.2161

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
20
Match the differential equation with the appropriate slope field.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the initial value problem.
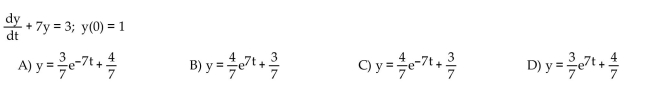
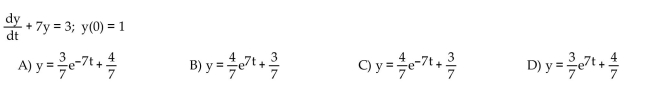

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
27
Solve the problem.
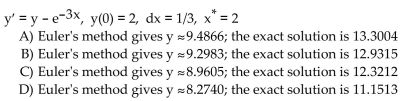
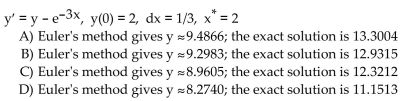

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the initial value problem.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
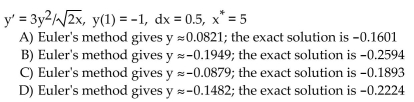
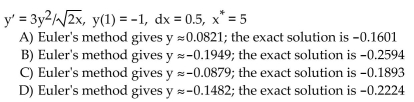

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the initial value problem.
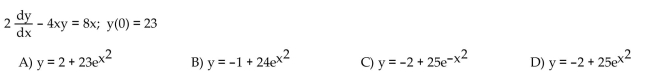
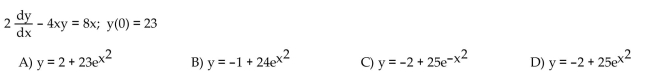

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the problem.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the problem.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the differential equation.
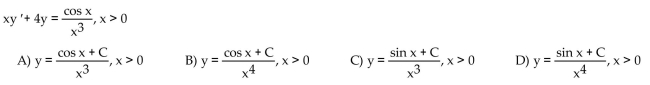
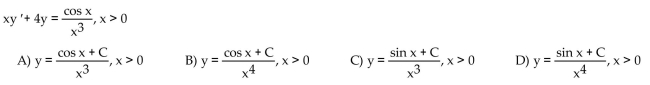

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
38
Obtain a slope field and add to its graphs of the solution curves passing through the given points.
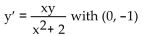
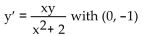

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
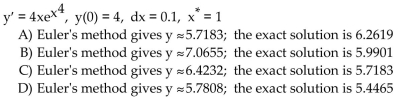
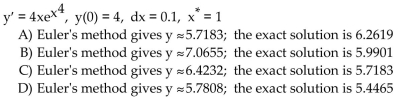

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
42
Determine which of the following equations is correct.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
A 200 gal tank is half full of distilled water. At time = 0, a solution containing 1 lb/gal of concentrate enters the tank at the rate of 4 gal/min, and the well-stirred mixture is withdrawn at the rate of 2 gal/min. When the tank
Is full, how many pounds of concentrate will it contain?
A) 100 pounds
B) 200 pounds
C) 120 pounds
D) 150 pounds
A 200 gal tank is half full of distilled water. At time = 0, a solution containing 1 lb/gal of concentrate enters the tank at the rate of 4 gal/min, and the well-stirred mixture is withdrawn at the rate of 2 gal/min. When the tank
Is full, how many pounds of concentrate will it contain?
A) 100 pounds
B) 200 pounds
C) 120 pounds
D) 150 pounds

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the initial value problem.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.

A) 5.01 min
B) 6.01 min
C) 8.01 min
D) 7.01 min

A) 5.01 min
B) 6.01 min
C) 8.01 min
D) 7.01 min

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
A tank contains 100 gal of fresh water. A solution containing 2 lb/gal of soluble lawn fertilizer runs into the tank at the rate of 1 gal/min, and the mixture is pumped out of the tank at the rate of 2 gal/min. Find the
Maximum amount of fertilizer in the tank and the time required to reach the maximum.
A) 60 pounds, 40 minutes
B) 48 pounds, 40 minutes
C) 48 pounds, 60 minutes
D) 50 pounds, 50 minutes
A tank contains 100 gal of fresh water. A solution containing 2 lb/gal of soluble lawn fertilizer runs into the tank at the rate of 1 gal/min, and the mixture is pumped out of the tank at the rate of 2 gal/min. Find the
Maximum amount of fertilizer in the tank and the time required to reach the maximum.
A) 60 pounds, 40 minutes
B) 48 pounds, 40 minutes
C) 48 pounds, 60 minutes
D) 50 pounds, 50 minutes

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the initial value problem.
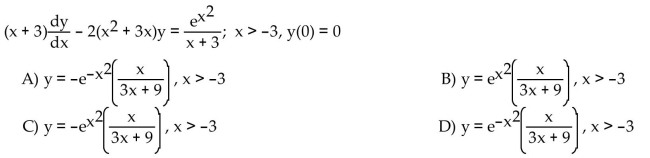
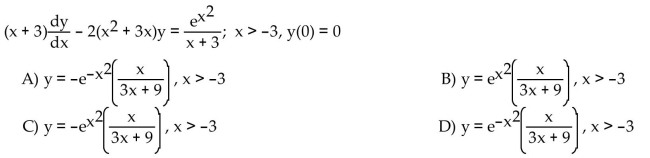

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the problem.
dy/dt = ky + f(t) is a population model where y is the population at time t and f(t) is some function to describe the net effect on the population. Assume k = .02 and y = 10,000 when t = 0. Solve the differential equation of y
When f(t) = -8t.
dy/dt = ky + f(t) is a population model where y is the population at time t and f(t) is some function to describe the net effect on the population. Assume k = .02 and y = 10,000 when t = 0. Solve the differential equation of y
When f(t) = -8t.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the initial value problem.
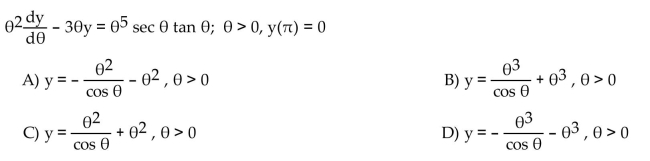
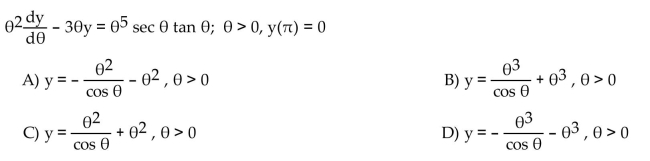

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the initial value problem.
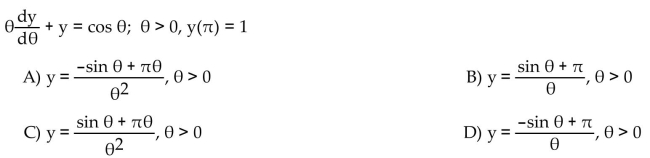
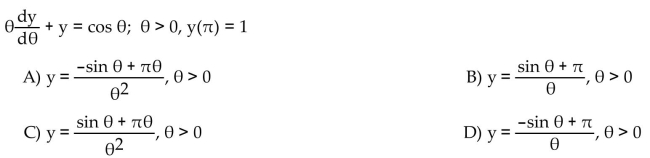

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
A tank initially contains 100 gal of brine in which 40 lb of salt are dissolved. A brine containing 2 lb/gal of salt runs into the tank at the rate of 4 gal/min. The mixture is kept uniform by stirring and flows out of the tank at
The rate of 3 gal/min. Find the solution to the differential equation that models the mixing process.
A tank initially contains 100 gal of brine in which 40 lb of salt are dissolved. A brine containing 2 lb/gal of salt runs into the tank at the rate of 4 gal/min. The mixture is kept uniform by stirring and flows out of the tank at
The rate of 3 gal/min. Find the solution to the differential equation that models the mixing process.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
dy/dt = ky + f(t) is a population model where y is the population at time t and f(t) is some function to describe the net effect on the population. Assume k = .02 and y = 10,000 when t = 0. Solve the differential equation of y
When f(t) = 11t.
dy/dt = ky + f(t) is a population model where y is the population at time t and f(t) is some function to describe the net effect on the population. Assume k = .02 and y = 10,000 when t = 0. Solve the differential equation of y
When f(t) = 11t.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
55
Determine which of the following equations is correct.
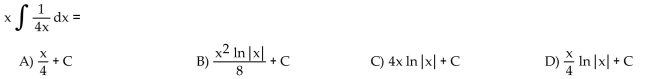
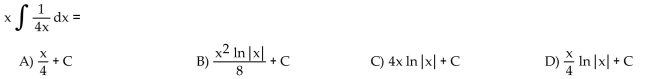

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
A 100 gal tank is half full of distilled water. At time = 0, a solution containing 2 lb/gal of concentrate enters the tank at the rate of 4 gal/min, and the well-stirred mixture is withdrawn at the rate of 3 gal/min. When the tank
Is full, how many pounds of concentrate will it contain?
A) 187.5 pounds
B) 200 pounds
C) 150 pounds
D) 175 pounds
A 100 gal tank is half full of distilled water. At time = 0, a solution containing 2 lb/gal of concentrate enters the tank at the rate of 4 gal/min, and the well-stirred mixture is withdrawn at the rate of 3 gal/min. When the tank
Is full, how many pounds of concentrate will it contain?
A) 187.5 pounds
B) 200 pounds
C) 150 pounds
D) 175 pounds

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the initial value problem.
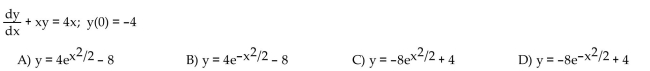
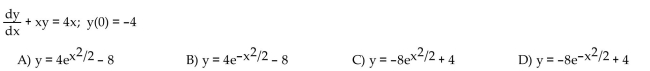

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
A tank initially contains 120 gal of brine in which 40 lb of salt are dissolved. A brine containing 2 lb/gal of salt runs into the tank at the rate of 9 gal/min. The mixture is kept uniform by stirring and flows out of the tank at
The rate of 6 gal/min. Write, in standard form, the differential equation that models the mixing process.
A tank initially contains 120 gal of brine in which 40 lb of salt are dissolved. A brine containing 2 lb/gal of salt runs into the tank at the rate of 9 gal/min. The mixture is kept uniform by stirring and flows out of the tank at
The rate of 6 gal/min. Write, in standard form, the differential equation that models the mixing process.


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the differential equation.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
61
Solve.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
62
Solve.
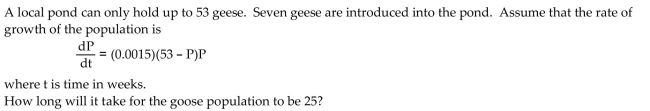
A) 22.26 weeks
B) 46.73 weeks
C) 26.02 weeks
D) 14.23 weeks
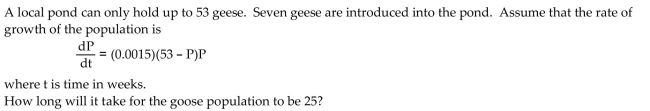
A) 22.26 weeks
B) 46.73 weeks
C) 26.02 weeks
D) 14.23 weeks

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
63
Identify equilibrium values and determine which are stable and which are unstable.
y = (y - 4)(y - 6)(y - 7)
A) y = 7 is a stable equilibrium value and y = 6 and y = 4 are unstable equilibria.
B) y = 4 is a stable equilibrium value and y = 6 and y = 7 are unstable equilibria.
C) y = 6 is a stable equilibrium value and y = 4 and y = 7 are unstable equilibria.
D) y = 5, y = 4 and y = 7 are unstable equilibria.
y = (y - 4)(y - 6)(y - 7)
A) y = 7 is a stable equilibrium value and y = 6 and y = 4 are unstable equilibria.
B) y = 4 is a stable equilibrium value and y = 6 and y = 7 are unstable equilibria.
C) y = 6 is a stable equilibrium value and y = 4 and y = 7 are unstable equilibria.
D) y = 5, y = 4 and y = 7 are unstable equilibria.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
64
Show that the curves are orthogonal.
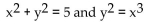
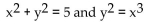

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
65
Construct a phase line. Identify signs of y and y .
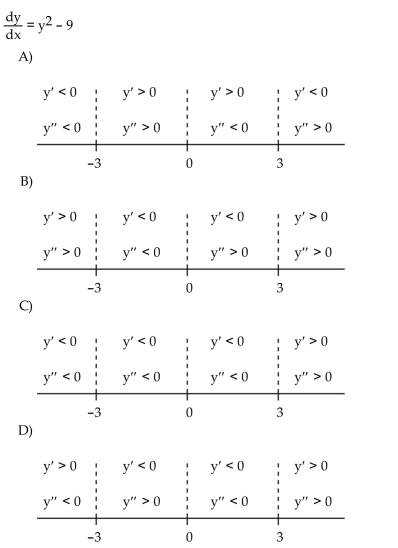


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
How many seconds after the switch in an RL circuit is closed will it take the current i to reach 20% of its steady state value? Express answer in terms of R and L and round coefficient to the nearest hundredth.
A) 0.22 L/R seconds
B) 1.81 L/R seconds
C) 1.61 L/R seconds
D) 0.42 L/R seconds
How many seconds after the switch in an RL circuit is closed will it take the current i to reach 20% of its steady state value? Express answer in terms of R and L and round coefficient to the nearest hundredth.
A) 0.22 L/R seconds
B) 1.81 L/R seconds
C) 1.61 L/R seconds
D) 0.42 L/R seconds

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
67
Solve.



Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.

A) -4.60 L/R seconds
B) -4.40 L/R seconds
C) 1.25 L/R seconds
D) 1.05 L/R seconds

A) -4.60 L/R seconds
B) -4.40 L/R seconds
C) 1.25 L/R seconds
D) 1.05 L/R seconds

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
69
Sketch several solution curves.
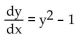
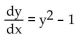

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
70
Show that the curves are orthogonal.
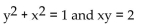
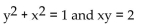

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
71
Construct a phase line. Identify signs of y and y .
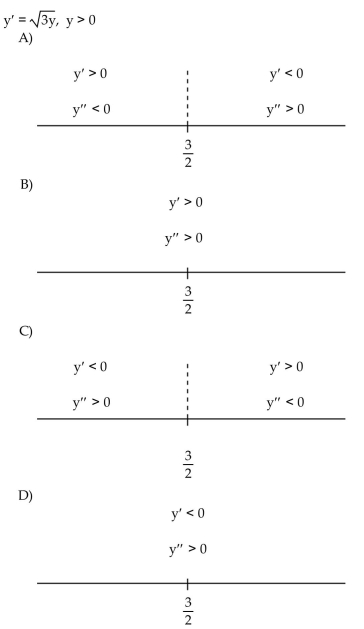
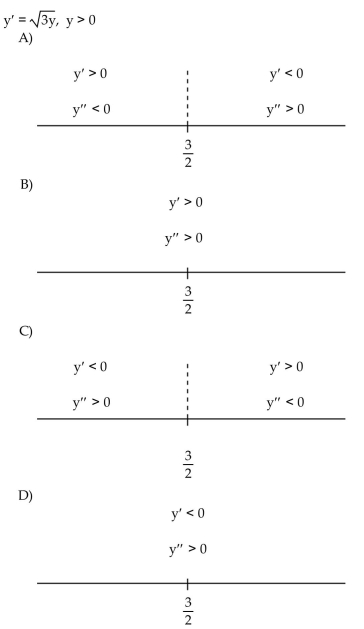

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
72
Identify equilibrium values and determine which are stable and which are unstable.
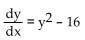
A) y = 4 is a stable equilibrium value and y = -4 is an unstable equilibrium.
B) y = -4 and y = 5 are stable equilibrium values.
C) y = -4 is a stable equilibrium value and y = 4 is an unstable equilibrium.
D) There are no equilibrium values.
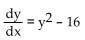
A) y = 4 is a stable equilibrium value and y = -4 is an unstable equilibrium.
B) y = -4 and y = 5 are stable equilibrium values.
C) y = -4 is a stable equilibrium value and y = 4 is an unstable equilibrium.
D) There are no equilibrium values.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
73
Find the orthogonal trajectories of the family of curves. Sketch several members of each family.
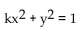
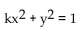

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
74
Identify equilibrium values and determine which are stable and which are unstable.
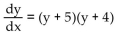
A) y = 4 is a stable equilibrium value and y = -5 is an unstable equilibrium.
B) y = -5 is a stable equilibrium value and y = 4 is an unstable equilibrium.
C) y = -4 is a stable equilibrium value and y = 5 is an unstable equilibrium.
D) y = 5 is a stable equilibrium value and y = 4 is an unstable equilibrium.
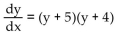
A) y = 4 is a stable equilibrium value and y = -5 is an unstable equilibrium.
B) y = -5 is a stable equilibrium value and y = 4 is an unstable equilibrium.
C) y = -4 is a stable equilibrium value and y = 5 is an unstable equilibrium.
D) y = 5 is a stable equilibrium value and y = 4 is an unstable equilibrium.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
75
Solve.
A 57-kg skateboarder on a 2-kg board starts coasting on level ground at 5 m/sec. Let k = 3.2 kg/sec. How long will it take the skater's speed to drop to 3 m/sec?
A) -9.42 sec
B) 9.10 sec
C) 0.32 sec
D) 9.42 sec
A 57-kg skateboarder on a 2-kg board starts coasting on level ground at 5 m/sec. Let k = 3.2 kg/sec. How long will it take the skater's speed to drop to 3 m/sec?
A) -9.42 sec
B) 9.10 sec
C) 0.32 sec
D) 9.42 sec

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
76
Solve.
A 60-kg skateboarder on a 1-kg board starts coasting on level ground at 8 m/sec. Let k = 3.2 kg/sec. About how far will the skater coast before reaching a complete stop?
A) 1536.00 m
B) 152.50 m
C) 24.00 m
D) 150.00 m
A 60-kg skateboarder on a 1-kg board starts coasting on level ground at 8 m/sec. Let k = 3.2 kg/sec. About how far will the skater coast before reaching a complete stop?
A) 1536.00 m
B) 152.50 m
C) 24.00 m
D) 150.00 m

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
77
Identify equilibrium values and determine which are stable and which are unstable.
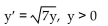
A) y = 0 is an unstable equilibrium value.
B) y = 7 is an unstable equilibrium value.
C) y = 0 is a stable equilibrium value.
D) There are no equilibrium values.
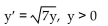
A) y = 0 is an unstable equilibrium value.
B) y = 7 is an unstable equilibrium value.
C) y = 0 is a stable equilibrium value.
D) There are no equilibrium values.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
78
Find the orthogonal trajectories of the family of curves. Sketch several members of each family.
y = -mx
y = -mx

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
79
Identify equilibrium values and determine which are stable and which are unstable.
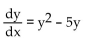
A) y = 0 and y = 5 are unstable equilibrium values.
B) y = 0 is a stable equilibrium value and y = 5 is an unstable equilibrium.
C) y = 5 is a stable equilibrium value and y = 0 is an unstable equilibrium.
D) There are no equilibrium values.
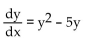
A) y = 0 and y = 5 are unstable equilibrium values.
B) y = 0 is a stable equilibrium value and y = 5 is an unstable equilibrium.
C) y = 5 is a stable equilibrium value and y = 0 is an unstable equilibrium.
D) There are no equilibrium values.

Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck
80
Construct a phase line. Identify signs of y and y .
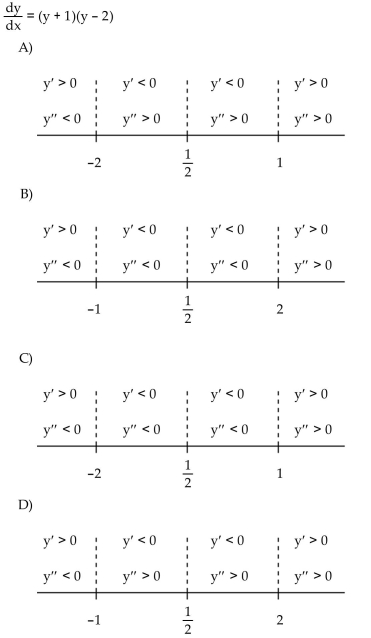


Unlock Deck
Unlock for access to all 90 flashcards in this deck.
Unlock Deck
k this deck


