Deck 8: A Transition
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/37
Play
Full screen (f)
Deck 8: A Transition
1
Is the ordered triple a solution to the given system of equations?
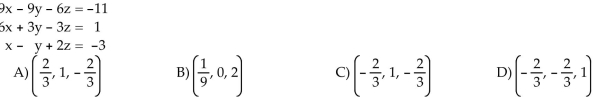
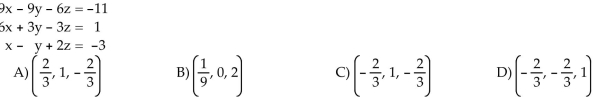
C
2
Is the ordered triple a solution to the given system of equations?
3x + 2y + z = -17 4x - 5y - z = 25
2x + y + 2z = -15
A) (-4 -5
-5  -1)
-1)
B) (-4 -1
-1  -5)
-5)
C) (-1 -5
-5  -4)
-4)
D) (-1 -4
-4  -5)
-5)
3x + 2y + z = -17 4x - 5y - z = 25
2x + y + 2z = -15
A) (-4
 -5
-5  -1)
-1)B) (-4
 -1
-1  -5)
-5)C) (-1
 -5
-5  -4)
-4)D) (-1
 -4
-4  -5)
-5)C
3
SOLVE


C
4
Solve using a system of two equations in two unknowns.
A retired couple has $150,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 6%. The rest they want to invest in AA bonds yielding 12% per
Year. How much should they invest in each to realize exactly $15,000 per year?
A) $100,000 at 6% and $50,000 at 12%
B) $90,000 at 6% and $60,000 at 12%
C) $100,000 at 12% and $50,000 at 6%
D) $110,000 at 12% and $40,000 at 6%
A retired couple has $150,000 to invest to obtain annual income. They want some of it invested in safe Certificates of Deposit yielding 6%. The rest they want to invest in AA bonds yielding 12% per
Year. How much should they invest in each to realize exactly $15,000 per year?
A) $100,000 at 6% and $50,000 at 12%
B) $90,000 at 6% and $60,000 at 12%
C) $100,000 at 12% and $50,000 at 6%
D) $110,000 at 12% and $40,000 at 6%

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
5
Solve using a system of two equations in two unknowns.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
6
Solve using a system of two equations in two unknowns.
Aviva has 67 dimes and nickels. The total value of the coins is $5.55. Find the number of each type of coin.
A) 44 nickels and 23 dimes
B) 23 nickels and 44 dimes
C) 25 nickels and 42 dimes
D) 28 nickels and 39 dimes
Aviva has 67 dimes and nickels. The total value of the coins is $5.55. Find the number of each type of coin.
A) 44 nickels and 23 dimes
B) 23 nickels and 44 dimes
C) 25 nickels and 42 dimes
D) 28 nickels and 39 dimes

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
7
SOLVE



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
8
SOLVE
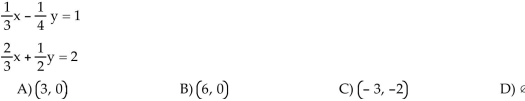
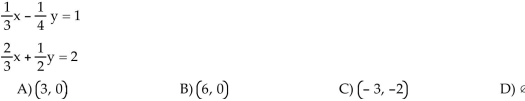

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
9
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
10
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
11
Is the ordered triple a solution to the given system of equations?
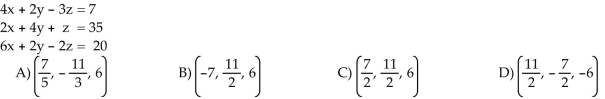
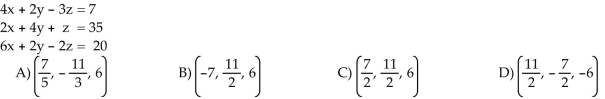

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
12
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
13
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
14
Is the ordered triple a solution to the given system of equations?
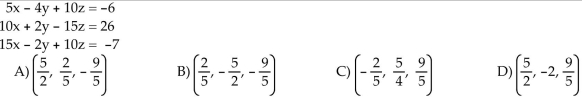
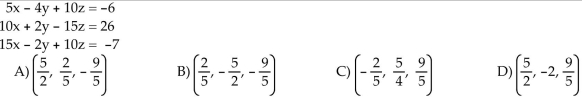

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
15
Is the ordered triple a solution to the given system of equations?
7x + 7y + z = 1 x + 8y + 8z = 8
9x + y + 9z = 9
A) (-1, 1, 1)
B) (0, 1, 0)
C) (0, 0, 1)
D) (1, -1, 1)
7x + 7y + z = 1 x + 8y + 8z = 8
9x + y + 9z = 9
A) (-1, 1, 1)
B) (0, 1, 0)
C) (0, 0, 1)
D) (1, -1, 1)

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
16
SOLVE



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
17
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
18
Solve using a system of two equations in two unknowns.
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $3.50. Another customer buys 3 hot dogs and 5 bags of potato chips for $6.75. Find the
Cost of each item.
A) $1.00 for a hot dog; $0.75 for a bag of potato chips
B) $0.75 for a hot dog; $1.00 for a bag of potato chips
C) $1.00 for a hot dog; $1.00 for a bag of potato chips
D) $1.25 for a hot dog; $1.00 for a bag of potato chips
A vendor sells hot dogs and bags of potato chips. A customer buys 2 hot dogs and 2 bags of potato chips for $3.50. Another customer buys 3 hot dogs and 5 bags of potato chips for $6.75. Find the
Cost of each item.
A) $1.00 for a hot dog; $0.75 for a bag of potato chips
B) $0.75 for a hot dog; $1.00 for a bag of potato chips
C) $1.00 for a hot dog; $1.00 for a bag of potato chips
D) $1.25 for a hot dog; $1.00 for a bag of potato chips

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
19
Is the ordered triple a solution to the given system of equations?



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
20
Is the ordered triple a solution to the given system of equations?
5x + 2y + z = -11 2x - 3y - z = 17
7x + y + 2z = -4
A) (-3, 0, 4)
B) (0, 6, -1)
C) (0, -6, 1)
D) (3, 0, -4)
5x + 2y + z = -11 2x - 3y - z = 17
7x + y + 2z = -4
A) (-3, 0, 4)
B) (0, 6, -1)
C) (0, -6, 1)
D) (3, 0, -4)

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
21
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
22
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
23
Solve.
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The income from the 5% and 6% investments is
The same as the income from the 8% investment. Find the amount invested at each rate.
A) At 5%: $10,000; at 6%: $5000; at 8%: $10,000
B) At 5%: $8000; at 6%: $10,000; at 8%: $7000
C) At 5%: $10,000; at 6%: $10,000; at 8%: $5000
D) At 5%: $5000; at 6%: $10,000; at 8%: $10,000
Linda invests $25,000 for one year. Part is invested at 5%, another part at 6%, and the rest at 8%. The total income from all 3 investments is $1600. The income from the 5% and 6% investments is
The same as the income from the 8% investment. Find the amount invested at each rate.
A) At 5%: $10,000; at 6%: $5000; at 8%: $10,000
B) At 5%: $8000; at 6%: $10,000; at 8%: $7000
C) At 5%: $10,000; at 6%: $10,000; at 8%: $5000
D) At 5%: $5000; at 6%: $10,000; at 8%: $10,000

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
24
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
25
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
26
Solve.
A basketball fieldhouse seats 15,000. Courtside seats sell for $10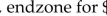
A) 4000 courtside; 3000 endzone; 8000 balcony
B) 3000 courtside; 3000 endzone; 8,000 balcony
C) 3000 courtside; 2000 endzone; 10,000 balcony
D) 3200 courtside; 1800 endzone; 10,000 balcony
A basketball fieldhouse seats 15,000. Courtside seats sell for $10
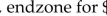
A) 4000 courtside; 3000 endzone; 8000 balcony
B) 3000 courtside; 3000 endzone; 8,000 balcony
C) 3000 courtside; 2000 endzone; 10,000 balcony
D) 3200 courtside; 1800 endzone; 10,000 balcony

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
27
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
28
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
29
Solve using a system of two equations in two unknowns.
The manager of a bulk foods establishment sells a trail mix for $7 per pound and premium cashews for $15 per pound. The manager wishes to make a 120-pound trail mix-cashew mixture
That will sell for $9 per pound. How many pounds of each should be used?
A) 75 lb of trail mix, 45 lb of cashews
B) 60 lb of trail mix, 60 lb of cashews
C) 30 lb of trail mix, 90 lb of cashews
D) 90 lb of trail mix, 30 lb of cashews
The manager of a bulk foods establishment sells a trail mix for $7 per pound and premium cashews for $15 per pound. The manager wishes to make a 120-pound trail mix-cashew mixture
That will sell for $9 per pound. How many pounds of each should be used?
A) 75 lb of trail mix, 45 lb of cashews
B) 60 lb of trail mix, 60 lb of cashews
C) 30 lb of trail mix, 90 lb of cashews
D) 90 lb of trail mix, 30 lb of cashews

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
30
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
31
Solve using a system of two equations in two unknowns.
A chemist needs 100 milliliters of a 70% solution but has only 66% and 86% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 90 milliliters of 66%; 30 milliliters of 86%
B) 90 milliliters of 66%; 20 milliliters of 86%
C) 80 milliliters of 66%; 20 milliliters of 86%
D) 20 milliliters of 66%; 80 milliliters of 86%
A chemist needs 100 milliliters of a 70% solution but has only 66% and 86% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
A) 90 milliliters of 66%; 30 milliliters of 86%
B) 90 milliliters of 66%; 20 milliliters of 86%
C) 80 milliliters of 66%; 20 milliliters of 86%
D) 20 milliliters of 66%; 80 milliliters of 86%

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
32
Solve.
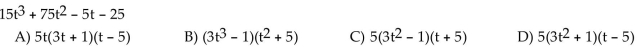
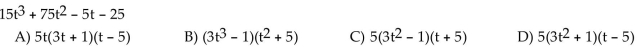

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
33
Solve.
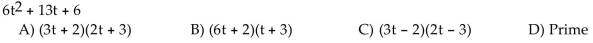
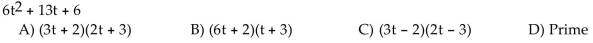

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
34
Solve.



Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
35
Solve.
Michaelʹs bank contains only nickels, dimes, and quarters. There are 59 coins in all, valued at $4.75. The number of nickels is 1 short of being three times the sum of the number of dimes and quarters
Together. How many dimes are in the bank?
A) 44
B) 7
C) 8
D) 13
Michaelʹs bank contains only nickels, dimes, and quarters. There are 59 coins in all, valued at $4.75. The number of nickels is 1 short of being three times the sum of the number of dimes and quarters
Together. How many dimes are in the bank?
A) 44
B) 7
C) 8
D) 13

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
36
Solve.
Michaelʹs bank contains only nickels, dimes, and quarters. There are 54 coins in all, valued at $4.30. The number of nickels is 2 short of being three times the sum of the number of dimes and quarters
Together. How many dimes are in the bank?
A) 6
B) 40
C) 8
D) 13
Michaelʹs bank contains only nickels, dimes, and quarters. There are 54 coins in all, valued at $4.30. The number of nickels is 2 short of being three times the sum of the number of dimes and quarters
Together. How many dimes are in the bank?
A) 6
B) 40
C) 8
D) 13

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
37
Solve using a system of two equations in two unknowns.
Dmitri needs 5 liters of a 7% solution of sulfuric acid for a research project in molecular biology. He has two unlimited supplies of sulfuric acid solution: 5% solution and 10% solution. How many
Liters of each solution should Dmitri use?
A) 5% solution: 3.5 L, 10% solution: 1.5 LB)5% solution: 3 L, 10% solution: 2 L
C) 5% solution: 2.5 L, 10% solution: 2.5 LD)5% solution: 2 L, 10% solution: 3 L
Dmitri needs 5 liters of a 7% solution of sulfuric acid for a research project in molecular biology. He has two unlimited supplies of sulfuric acid solution: 5% solution and 10% solution. How many
Liters of each solution should Dmitri use?
A) 5% solution: 3.5 L, 10% solution: 1.5 LB)5% solution: 3 L, 10% solution: 2 L
C) 5% solution: 2.5 L, 10% solution: 2.5 LD)5% solution: 2 L, 10% solution: 3 L

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck


