Deck 22: Signal Transduction Mechanisms I: Electrical and Synaptic Signaling in Neurons
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/10
Play
Full screen (f)
Deck 22: Signal Transduction Mechanisms I: Electrical and Synaptic Signaling in Neurons
1
The Truth About Nerve Cells. For each of the following statements, indicate whether it is true of all nerve cells (A), of some nerve cells (S), or of no nerve cells (N).
(a)Axonal endings are in direct contact with the cells they innervate.
(b)The resting membrane potential of the axonal membrane is positive.
(c)Nodes of Ranvier are found at regular intervals along the axon.
(d)The resting potential of the membrane is much closer to the equilibrium potential for potassium ions than to that for sodium ions because the permeability of the axonal membrane is much greater for potassium than for sodium.
(e)Excitation of the membrane results in a transient increase in its permeability to sodium ions.
(f)The electrical potential across the membrane of the axon can be easily measured using electrodes.
(g)Calcium elevation stimulates release of neurosecretory vesicles containing serotonin.
(a)Axonal endings are in direct contact with the cells they innervate.
(b)The resting membrane potential of the axonal membrane is positive.
(c)Nodes of Ranvier are found at regular intervals along the axon.
(d)The resting potential of the membrane is much closer to the equilibrium potential for potassium ions than to that for sodium ions because the permeability of the axonal membrane is much greater for potassium than for sodium.
(e)Excitation of the membrane results in a transient increase in its permeability to sodium ions.
(f)The electrical potential across the membrane of the axon can be easily measured using electrodes.
(g)Calcium elevation stimulates release of neurosecretory vesicles containing serotonin.
(a)
The axonal endings of neurons that innervate muscles are in direct contact with muscle cells. However, there is no direct contact between neurons that communicate with other neurons. There is a gap between the axon of on cell and the dendrites of another called the synapse.
Hence, the given statement is
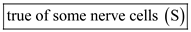 .
.
(b)
During an action potential, the influx of sodium ions makes the membrane potential positive. So, in resting state, the membrane potential of the axonal membrane is negative always.
Hence, the given statement is true of
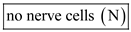 .
.
(c)
The nodes of Ranvier are present at intervals along myelinated axons. However, not all axons are surrounded by a myelin sheath.
Hence, the given statement is
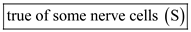 .
.
(d)
At rest, the membranes of all axons are naturally more permeable to potassium than sodium. As a result, the resting membrane potential is closer to the equilibrium potential of potassium.
Hence, the given statement is true of
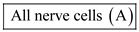 (e)
(e)
Excitation of the membrane triggers the opening of sodium channels at the axon hillock. As a result, the membrane becomes more permeable to sodium and depolarization occurs. However, all the nerve cells do not get excited with transient increase in permeability of sodium ions.
Hence, the given statement is
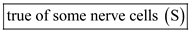 .
.
(f)
Not all axons are large enough to be measured with electrodes. For studies requiring the measurement of electrical potentials, giant squid axons are used because they are large enough to be connected to electrodes.
Hence, the given statement is
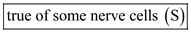 .
.
(g)
Serotonin release is not influenced by the elevation of calcium levels.
Hence, the given statement is true of
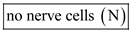 .
.
The axonal endings of neurons that innervate muscles are in direct contact with muscle cells. However, there is no direct contact between neurons that communicate with other neurons. There is a gap between the axon of on cell and the dendrites of another called the synapse.
Hence, the given statement is
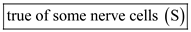 .
.(b)
During an action potential, the influx of sodium ions makes the membrane potential positive. So, in resting state, the membrane potential of the axonal membrane is negative always.
Hence, the given statement is true of
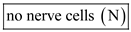 .
.(c)
The nodes of Ranvier are present at intervals along myelinated axons. However, not all axons are surrounded by a myelin sheath.
Hence, the given statement is
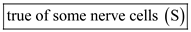 .
.(d)
At rest, the membranes of all axons are naturally more permeable to potassium than sodium. As a result, the resting membrane potential is closer to the equilibrium potential of potassium.
Hence, the given statement is true of
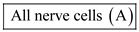 (e)
(e)Excitation of the membrane triggers the opening of sodium channels at the axon hillock. As a result, the membrane becomes more permeable to sodium and depolarization occurs. However, all the nerve cells do not get excited with transient increase in permeability of sodium ions.
Hence, the given statement is
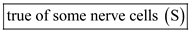 .
.(f)
Not all axons are large enough to be measured with electrodes. For studies requiring the measurement of electrical potentials, giant squid axons are used because they are large enough to be connected to electrodes.
Hence, the given statement is
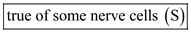 .
.(g)
Serotonin release is not influenced by the elevation of calcium levels.
Hence, the given statement is true of
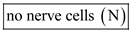 .
. 2
The Resting Membrane Potential. The Goldman equation is used to calculate Vm, the resting potential of a biological membrane. As presented in the chapter, this equation contains terms for sodium, potassium, and chloride ions only.
(a)Why do only these three ions appear in the Goldman equation as it applies to nerve impulse transmission
(b)Suggest a more general formulation for the Goldman equation that would be applicable to membranes that might be selectively permeable to other monovalent ions as well.
(c)How much would the resting potential of the membrane change if the relative permeability for sodium ions were 1.0 instead of 0.01
(d)Would you expect a plot of V m versus the relative permeability of the membrane to sodium to be linear Why or why not
(a)Why do only these three ions appear in the Goldman equation as it applies to nerve impulse transmission
(b)Suggest a more general formulation for the Goldman equation that would be applicable to membranes that might be selectively permeable to other monovalent ions as well.
(c)How much would the resting potential of the membrane change if the relative permeability for sodium ions were 1.0 instead of 0.01
(d)Would you expect a plot of V m versus the relative permeability of the membrane to sodium to be linear Why or why not
 The Goldman equation was devised to determine the effects of ions on the membrane potential collectively. When a neuron is at rest, the membrane is selectively permeable to potassium
The Goldman equation was devised to determine the effects of ions on the membrane potential collectively. When a neuron is at rest, the membrane is selectively permeable to potassium 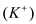 and it naturally leaks out of the membrane. The movement of potassium makes the membrane potential more negative. Although the permeability is lower, the nerve cell is also permeable to sodium
and it naturally leaks out of the membrane. The movement of potassium makes the membrane potential more negative. Although the permeability is lower, the nerve cell is also permeable to sodium 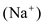 and chloride
and chloride 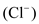 .
.Unlike the Nernst equation which only considers one ion at a time, the Goldman equation acknowledges that more than one type of ion moves across the membrane. Other ions have an insignificant amount of permeability. Therefore, only potassium
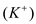 , sodium
, sodium 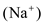 and chloride
and chloride 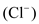 appear in the Goldman equation.
appear in the Goldman equation.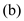 In order to suggest a more general formulation for the Goldman equation, consider the full version of the equation.
In order to suggest a more general formulation for the Goldman equation, consider the full version of the equation.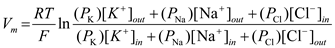 The variable
The variable  is the resting potential and
is the resting potential and  is the relative permeability of the specified ion. Before additional monovalent ions can be added to the equation, determine whether the ions have a positive valence, like potassium
is the relative permeability of the specified ion. Before additional monovalent ions can be added to the equation, determine whether the ions have a positive valence, like potassium 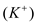 and sodium
and sodium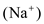 , or negative valence, like chloride
, or negative valence, like chloride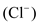 . If the valence is negative, the ion concentration inside will be the numerator and the concentration outside will be the denominator.
. If the valence is negative, the ion concentration inside will be the numerator and the concentration outside will be the denominator. Therefore, a general formulation for the Goldman equation that would be applicable to membranes permeable to any negative ion
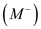 as well as potassium
as well as potassium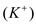 , sodium
, sodium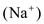 , and chloride
, and chloride 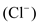 would be:
would be: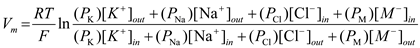
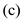 The ion concentrations of sodium in a mammalian neuron is
The ion concentrations of sodium in a mammalian neuron is 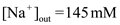 and
and  , for potassium is
, for potassium is 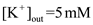 ,
, 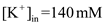 and for chloride is
and for chloride is  and
and 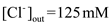 . Under general circumstances, the relative permeability of sodium ions is 45% of chloride ions and 4% of potassium ions. So, the ratio of
. Under general circumstances, the relative permeability of sodium ions is 45% of chloride ions and 4% of potassium ions. So, the ratio of  . So, if the relative permeability for sodium ions were 0.01, then the ratio of
. So, if the relative permeability for sodium ions were 0.01, then the ratio of 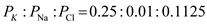 . The
. The  at relative permeability for sodium ions were 0.01 is as follows:
at relative permeability for sodium ions were 0.01 is as follows:  Likewise, if relative permeability for sodium ions were 1.0, then the ratio of
Likewise, if relative permeability for sodium ions were 1.0, then the ratio of 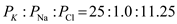 .
. So, the
So, the  at relative permeability 0.01 and 1.0 is
at relative permeability 0.01 and 1.0 is 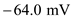 . In general, the resting membrane potential is
. In general, the resting membrane potential is 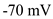 . So, the difference between
. So, the difference between 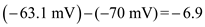 . Therefore, the change is
. Therefore, the change is 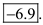
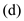 In the given case, graph would not be liner, so the answer is no because
In the given case, graph would not be liner, so the answer is no because  is proportional to the logarithm of the expression that contains the term for sodium permeability.
is proportional to the logarithm of the expression that contains the term for sodium permeability. 3
Patch Clamping. Patch-clamp instruments enable researchers to measure the opening and closing of a single channel in a membrane. A typical acetylcholine receptor channel passes about 5 pA (picoamperes)of ionic current (1 picoampere = 10 -12 ampere)over a period of about 5 msec at -60 mV.
(a)Given that an electrical current of 1 A is about 6.2 × 10 18 electrical charges per second, how many ions (potassium or sodium)pass through the channel during the time it is open
(b)Do you think the opening of a single receptor channel would be sufficient to depolarize a postsynaptic membrane Why or why not
(a)Given that an electrical current of 1 A is about 6.2 × 10 18 electrical charges per second, how many ions (potassium or sodium)pass through the channel during the time it is open
(b)Do you think the opening of a single receptor channel would be sufficient to depolarize a postsynaptic membrane Why or why not
(a)
The electrical current data provided is the standard data that will be used to determine how many ions pass through the acetylcholine receptor channel.
First, setup a proportion to determine how many charges pass through the channel. Remember to convert picoAmperes to Amperes.
(1 A)/ (6.2 * 10 18 charges per second)= (5 * 10 -12 A)/ x
Solve and simplify the proportion. The variable x represents the number of charges that enter the channel per second.
x = 3.1 * 10 7 or 31 million charges per second
According to this result, 31 million charges enter the acetlycholine receptor per second; however, it is only open for 5 miliseconds. You can find the number of ions that enter during this time frame by setting up another proportion.
(3.1 * 10 7 )/ 1 second = x /.005 seconds
In the above equation, x represents the number of ions that enter the channel after 5 milliseconds or 0.005 seconds. Solve and simplify the equation.
The number of ions that enter the acetlycholine receptor channel after 5 msec is 155, 000.
(b)
The opening of the receptor would be sufficient to depolarize a postsynaptic membrane. Sodium depolarizes the membrane at 6 million ions per second and the acetylcholine receptor releases 31 million ions per second.
The electrical current data provided is the standard data that will be used to determine how many ions pass through the acetylcholine receptor channel.
First, setup a proportion to determine how many charges pass through the channel. Remember to convert picoAmperes to Amperes.
(1 A)/ (6.2 * 10 18 charges per second)= (5 * 10 -12 A)/ x
Solve and simplify the proportion. The variable x represents the number of charges that enter the channel per second.
x = 3.1 * 10 7 or 31 million charges per second
According to this result, 31 million charges enter the acetlycholine receptor per second; however, it is only open for 5 miliseconds. You can find the number of ions that enter during this time frame by setting up another proportion.
(3.1 * 10 7 )/ 1 second = x /.005 seconds
In the above equation, x represents the number of ions that enter the channel after 5 milliseconds or 0.005 seconds. Solve and simplify the equation.
The number of ions that enter the acetlycholine receptor channel after 5 msec is 155, 000.
(b)
The opening of the receptor would be sufficient to depolarize a postsynaptic membrane. Sodium depolarizes the membrane at 6 million ions per second and the acetylcholine receptor releases 31 million ions per second.
4
The Equilibrium Potential. Answer each of the following questions with respect to E Cl , the equilibrium potential for chloride ions. The chloride ion concentration inside the squid giant axon can vary from 50 to 150 mM.
(a)Before doing any calculations, predict whether E Cl will be positive or negative. Explain.
(b)Now calculate E Cl assuming an internal chloride concentration of 50 mM.
(c)How much difference would it make in the value of E Cl if the internal chloride concentration were 150 mM instead
(a)Before doing any calculations, predict whether E Cl will be positive or negative. Explain.
(b)Now calculate E Cl assuming an internal chloride concentration of 50 mM.
(c)How much difference would it make in the value of E Cl if the internal chloride concentration were 150 mM instead

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
5
Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles:
[K + ]: 150 m M in cell, 4.6 m M in serum
[Na + ]: 10 m M in cell, 145 m M in serum
[Ca 2+ ]: 0.001 m M in cell, 6 m M in serum
Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell.
(a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed.
(b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV)
(c)The more positive membrane potential in region
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_bfb0_a881_77457a19465d_SM894_11.jpg) of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane
of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane
(d)How might you distinguish between the possibilities suggested in part c
(e)The rapid decrease in membrane potential that is occurring in region
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c1_a881_3d7ba6f5a790_SM894_11.jpg) is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region
is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c2_a881_33d746a645fc_SM894_11.jpg) of the curve
of the curve
FIGURE The Action Potential of a Muscle Cell of the Human Heart.
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c3_a881_69d006469347_SM894_00.jpg)
[K + ]: 150 m M in cell, 4.6 m M in serum
[Na + ]: 10 m M in cell, 145 m M in serum
[Ca 2+ ]: 0.001 m M in cell, 6 m M in serum
Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell.
(a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed.
(b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV)
(c)The more positive membrane potential in region
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_bfb0_a881_77457a19465d_SM894_11.jpg) of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane
of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c
(e)The rapid decrease in membrane potential that is occurring in region
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c1_a881_3d7ba6f5a790_SM894_11.jpg) is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region
is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region ![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c2_a881_33d746a645fc_SM894_11.jpg) of the curve
of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.
![Heart Throbs. An understanding of muscle cell stimulation involves some of the same principles as nerve cell stimulation, except that calcium ions play an important role in the former. The following ion concentrations are typical of those in human heart muscle and in the serum that bathes the muscles: [K + ]: 150 m M in cell, 4.6 m M in serum [Na + ]: 10 m M in cell, 145 m M in serum [Ca 2+ ]: 0.001 m M in cell, 6 m M in serum Figure depicts the change in membrane potential with time upon stimulation of a cardiac muscle cell. (a)Calculate the equilibrium potential for each of the three ions, given the concentrations listed. (b)Why is the resting membrane potential significantly more negative than that of the squid axon (-75 mV versus -60 mV) (c)The more positive membrane potential in region of the graph could in theory be due to the movement across the membrane of one or both of two cations. Which cations are they, and in what direction would you expect each of them to move across the membrane (d)How might you distinguish between the possibilities suggested in part c (e)The rapid decrease in membrane potential that is occurring in region is caused by the outward movement of potassium ions. What are the driving forces that cause potassium to leave the cell at this point Why aren't the same forces operative in region of the curve FIGURE The Action Potential of a Muscle Cell of the Human Heart.](https://storage.examlex.com/SM894/11eb69ec_f639_e6c3_a881_69d006469347_SM894_00.jpg)

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
6
The All-or-None Response of Membrane Excitation. A nerve cell membrane exhibits an all-or-none response to excitation; that is, the magnitude of the response is independent of the magnitude of the stimulus, once a threshold value is exceeded.
(a)Explain in your own words why this is so.
(b)If every neuron exhibits an all-or-none response, how do you suppose the nervous system of an animal can distinguish different intensities of stimulation How do you think your own nervous system can tell the difference between a warm iron and a hot iron or between a chamber orchestra and a rock band
(a)Explain in your own words why this is so.
(b)If every neuron exhibits an all-or-none response, how do you suppose the nervous system of an animal can distinguish different intensities of stimulation How do you think your own nervous system can tell the difference between a warm iron and a hot iron or between a chamber orchestra and a rock band

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
7
One-Way Propagation. Why does an action potential move in only one direction down the axon

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
8
Multiple Sclerosis and Action Potential Propagation. Multiple sclerosis (MS)is an autoimmune disease that attacks myelinated nerves and degrades the myelin sheath around them. How do you think the propagation of action potentials would be affected in a nerve cell that has been damaged in a patient with MS

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
9
Stricken by Strychnine. The plant alkaloid strychnine is a poison that occurs at high levels in a particular deciduous tree ( Strychnos nux-vomica)found in India. It is an effective poison for killing rodents and other small vertebrates. In small doses, it has been used illegally by athletes as a stimulant. Strychnine antagonizes the glycine receptor, which, like the GABA receptor, is a ligand-gated chloride channel. Explain why strychnine has the effects it has.

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck
10
Down and Out. Endocannabinoids are produced by postsynaptic neurons but act on receptors (CB1 receptors)in presynaptic neurons. One type of neuron that is a target of endocannabinoids is glutamatergic neurons (that is, neurons that release glutamate as a neurotransmitter).
(a)CB1 agonists such as THC reduce calcium influx by blocking the activity of voltage-dependent calcium channels. What effect would this have on the release of glutamate
(b)Glutamate causes the membrane of postsynaptic neurons to become hyperpolarized. How would THC be expected to affect the rate of nerve impulse transmission in postsynaptic neurons that make synapses with the glutamatergic neuron
(a)CB1 agonists such as THC reduce calcium influx by blocking the activity of voltage-dependent calcium channels. What effect would this have on the release of glutamate
(b)Glutamate causes the membrane of postsynaptic neurons to become hyperpolarized. How would THC be expected to affect the rate of nerve impulse transmission in postsynaptic neurons that make synapses with the glutamatergic neuron

Unlock Deck
Unlock for access to all 10 flashcards in this deck.
Unlock Deck
k this deck


