Deck 11: Annuities, Stocks, and Bonds
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/174
Play
Full screen (f)
Deck 11: Annuities, Stocks, and Bonds
1
To help you review, the numbers in brackets show the section in which the topic was discussed.
Find the amounts of this annuities.

Find the amounts of this annuities.

This is a problem of finding the amount of an annuity.
The following information is given,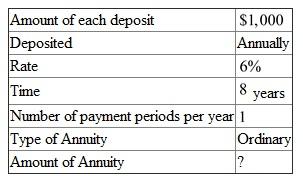 There are
There are 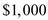 payment periods.
payment periods.
The interest rate per payment period is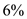 .
.
Look across the top of the Amount of an Annuity Table for 6% and down the side for 8 periods to find 9.89747.
Recall the formula for finding amount of an annuity,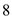 Or,
Or, 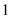 Using
Using 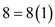 , and
, and 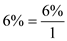 in the formula above,
in the formula above, 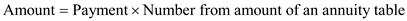 Therefore, the amount of annuity is
Therefore, the amount of annuity is 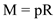 .
.
The following information is given,
 There are
There are 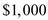 payment periods.
payment periods. The interest rate per payment period is
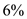 .
. Look across the top of the Amount of an Annuity Table for 6% and down the side for 8 periods to find 9.89747.
Recall the formula for finding amount of an annuity,
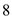 Or,
Or, 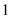 Using
Using 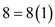 , and
, and 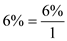 in the formula above,
in the formula above, 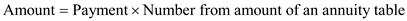 Therefore, the amount of annuity is
Therefore, the amount of annuity is 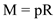 .
. 2
Find the present value of this annuities.


This is a problem of finding the present value of an annuity,
The following information is given,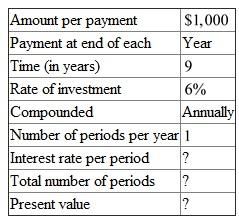 There are
There are 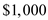 periods.
periods.
The interest rate per period is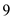 .
.
Look across the top of the Present Value of an Annuity Table for 6% and down the side for 9 periods to find 6.80169.
Recall the formula for finding Present Value of an Annuity, Or,
Or, 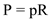 Using
Using 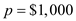 , and
, and 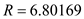 in the formula above,
in the formula above,  Therefore, the present value is
Therefore, the present value is 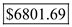 .
.
The following information is given,
 There are
There are 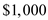 periods.
periods. The interest rate per period is
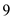 .
. Look across the top of the Present Value of an Annuity Table for 6% and down the side for 9 periods to find 6.80169.
Recall the formula for finding Present Value of an Annuity,
 Or,
Or, 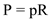 Using
Using 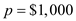 , and
, and 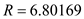 in the formula above,
in the formula above,  Therefore, the present value is
Therefore, the present value is 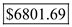 .
. 3
Find the amount of the following ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples 1 and 2.)
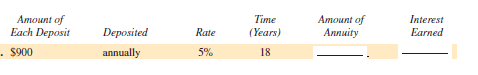
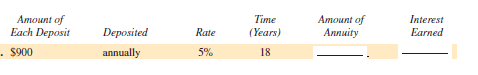
The following table is given, 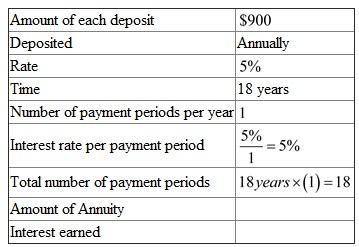 There are
There are 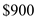 payment periods.
payment periods.
The interest rate per payment period is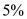 .
.
Look across the top of the amount of an annuity table for and down the side for
and down the side for 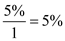 periods to find
periods to find 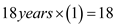 .
.
Recall the formula for finding Amount of an Annuity,
"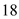 , or
, or 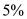 "
"
Use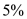 , and
, and 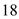 in the formula above,
in the formula above, 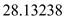 Recall the formula, Finding Interest of an Annuity,
Recall the formula, Finding Interest of an Annuity,
"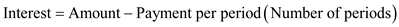 , or
, or 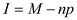 "
"
Use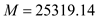 ,
, 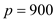 and
and 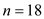 in the formula above,
in the formula above,  Complete the table,
Complete the table, 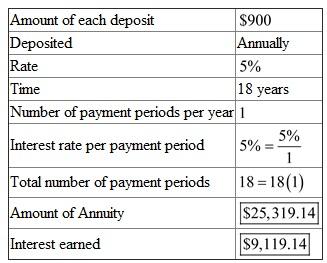
 There are
There are 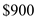 payment periods.
payment periods. The interest rate per payment period is
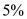 .
. Look across the top of the amount of an annuity table for
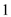 and down the side for
and down the side for 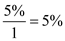 periods to find
periods to find 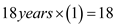 .
. Recall the formula for finding Amount of an Annuity,
"
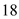 , or
, or 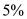 "
"Use
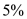 , and
, and 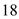 in the formula above,
in the formula above, 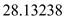 Recall the formula, Finding Interest of an Annuity,
Recall the formula, Finding Interest of an Annuity, "
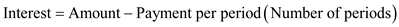 , or
, or 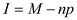 "
"Use
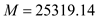 ,
, 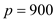 and
and 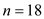 in the formula above,
in the formula above,  Complete the table,
Complete the table, 
4
Solve the following application problems.
CHILD-CARE PAYMENTS Monique Chaney places $250 of her quarterly child support check into an annuity for the education of her child. She does this at the beginning of each quarter for 8 years into an account paying 8% per year, compounded quarterly. Find (a) the amount of the annuity ____________and (b) the interest earned. ____________
CHILD-CARE PAYMENTS Monique Chaney places $250 of her quarterly child support check into an annuity for the education of her child. She does this at the beginning of each quarter for 8 years into an account paying 8% per year, compounded quarterly. Find (a) the amount of the annuity ____________and (b) the interest earned. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
5
Solve this application problems. Round to the nearest cent.
PAYING FOR COLLEGE Tom Potter estimates that his daughter's college needs, beginning in 8 years, will be $3600 at the end of each quarter for 4 years. (a) Find the total ____________ (b) amount needed in 8 years assuming 8% compounded quarterly. (b) Will he have enough money available in 8 years if he invests $700 at the end of each quarter for the next 8 years at 8% compounded quarterly? ____________
PAYING FOR COLLEGE Tom Potter estimates that his daughter's college needs, beginning in 8 years, will be $3600 at the end of each quarter for 4 years. (a) Find the total ____________ (b) amount needed in 8 years assuming 8% compounded quarterly. (b) Will he have enough money available in 8 years if he invests $700 at the end of each quarter for the next 8 years at 8% compounded quarterly? ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
6
Find the amount of the payment needed to accumulate the indicated amount in a sinking fund. Round to the nearest cent. (See Examples.)
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
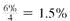 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

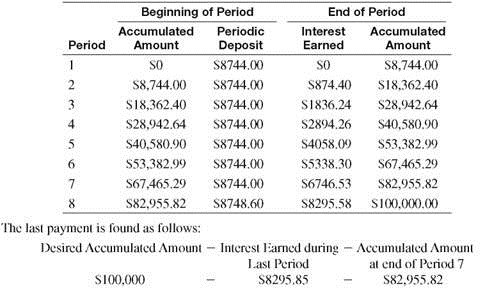
Setting up a Sinking Fund Table
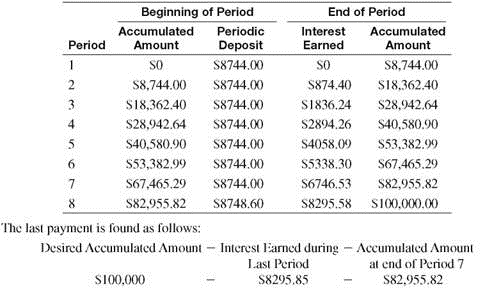
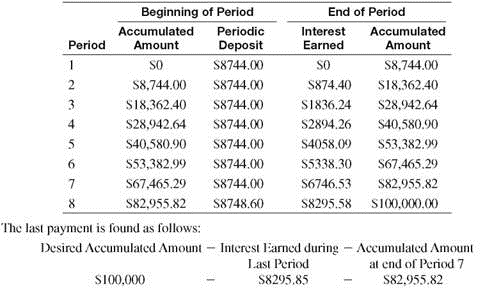
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.
$32,000, money earns 6% compounded quarterly, 3 years____________
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
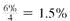 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.

$32,000, money earns 6% compounded quarterly, 3 years____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
7
Solve each application problem. Round to the nearest cent.
NEW MACHINERY Smith Dry Cleaning must buy new cleaning machines in 7 years for $120,000. The firm sets up a sinking fund for this purpose. Find the payment into the fund at the end of each year if money in the fund earns 10% compounded annually.
NEW MACHINERY Smith Dry Cleaning must buy new cleaning machines in 7 years for $120,000. The firm sets up a sinking fund for this purpose. Find the payment into the fund at the end of each year if money in the fund earns 10% compounded annually.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
8
Find the following from the stock table on pages 465 and 466. (See Example 1.)
Volume for Rex Stores (RSC)___________
Volume for Rex Stores (RSC)___________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
9
Ignore commissions and find the cost for the following stock purchases at the closing price for the week. Then find the annual dividend that will be paid on those shares.
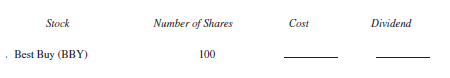

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
10
Find the PE ratio for each of the following. Round all answers to the nearest whole number. (See Example 4.)
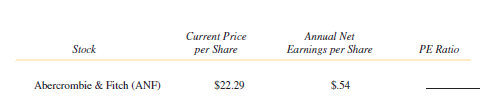
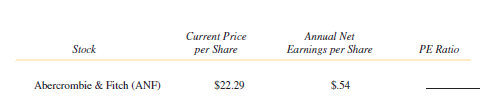

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
11
Find the cost, including sales charges of $10 per bond, for each of the following purchases. (See Example 3.)
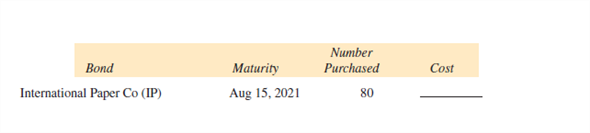
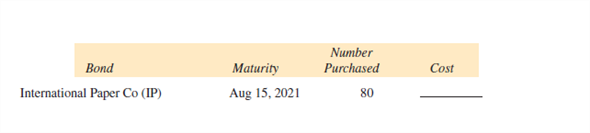

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
12
Li is amazed that he will be able to accumulate over $600,000. However, he knows that inflation will increase his cost of living significantly in 30 years. He assumes 3% inflation and wants to find the income he needs at age 67 to have the same purchasing power as $40,000 today. ( Hint: Look at inflation in Section and use the compound interest table in Section.) ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
13
Find the present value of this annuities.



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
14
Find the amount of the following ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples 1 and 2.)
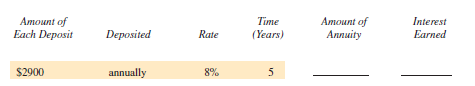
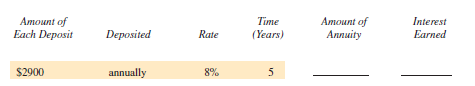

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the following application problems.
RETIREMENT Jason Horton works for Chevron as a welder on offshore drilling rigs. His retirement plan contributions are $3800 at the beginning of each 6-month period. Assume that the account grows at 6% compounded semiannually for 15 years. Find the (a) future value of the annuity ____________and (b) the interest earned. ____________
RETIREMENT Jason Horton works for Chevron as a welder on offshore drilling rigs. His retirement plan contributions are $3800 at the beginning of each 6-month period. Assume that the account grows at 6% compounded semiannually for 15 years. Find the (a) future value of the annuity ____________and (b) the interest earned. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the following application problems. Round to the nearest cent.
VAN PURCHASE In 4 years, Jennifer Videtto will need a delivery van that will require a down payment of $10,000 with payments of $1200 per month for 36 months. (a) Find the total amount needed in 4 years assuming 12 compounded monthly. (b) Will she have enough money available if she invests $1000 at the end of each month for the next 4 years at 12% compounded monthly?
VAN PURCHASE In 4 years, Jennifer Videtto will need a delivery van that will require a down payment of $10,000 with payments of $1200 per month for 36 months. (a) Find the total amount needed in 4 years assuming 12 compounded monthly. (b) Will she have enough money available if she invests $1000 at the end of each month for the next 4 years at 12% compounded monthly?

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
17
Solve this application problems. Round to the nearest cent.
Abel Plumbing saves $12,000 at the end of every semiannual period in an account earning 6% compounded semiannually to replace several of its trucks in 5 years. Find the lump sum that could be deposited today that will grow to the same future value. ____________
Abel Plumbing saves $12,000 at the end of every semiannual period in an account earning 6% compounded semiannually to replace several of its trucks in 5 years. Find the lump sum that could be deposited today that will grow to the same future value. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
18
Solve the application problem. Round to the nearest cent.
NEW AUDITORIUM The membership of the Green Fields Baptist Church is large and growing rapidly. The leaders of the church are planning to remodel the auditorium with special features for their televised broadcasts at a cost of $2,800,000 in 5 years. The membership has set up a sinking fund with the idea of making a payment at the end of each quarter. Find the payment needed if money earns 8% compounded quarterly. ____________
NEW AUDITORIUM The membership of the Green Fields Baptist Church is large and growing rapidly. The leaders of the church are planning to remodel the auditorium with special features for their televised broadcasts at a cost of $2,800,000 in 5 years. The membership has set up a sinking fund with the idea of making a payment at the end of each quarter. Find the payment needed if money earns 8% compounded quarterly. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
19
Find the following from the stock table on pages 465 and 466. (See Example 1.)
Volume for Ball Corporation (BLL) _____________
Volume for Ball Corporation (BLL) _____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
20
Ignore commissions and find the cost for this stock purchases at the closing price for the week. Then find the annual dividend that will be paid on those shares.
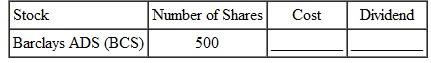
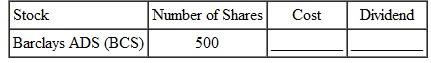

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
21
Find the PE ratio for each of the following. Round all answers to the nearest whole number. (See Example 4.)
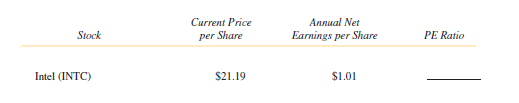
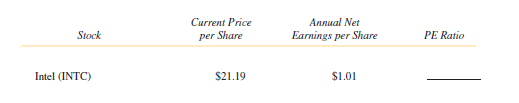

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
22
Find the cost, including sales charges of $10 per bond, for each of the following purchases. (See Example 3.)
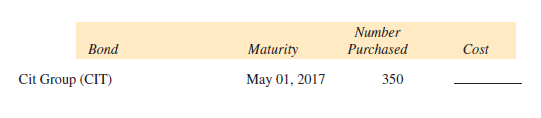
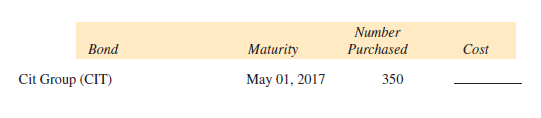

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
23
AMERICAN RIVER COLLEGE
www.arc.losrios.edu
Facts:
• 1955: Founded
• 2010: About 35,000 students
• 2011: 58% of the students are under 30
• 2011: 50.3% of students are women
American River offers students a choice of more than 70 different majors of study, including biology, engineering, hospitality management, mortuary science, collision repair, business, and even fire technology. College personnel work closely with students to help them find financial aid.
Amazingly, about one-half of the students at American River College receive some kind of financial aid. Roman Rodriguez had 3 years of experience when he went to work in Human Resources at American River College at a salary of $42,000. He began work on his 30th birthday. The college matches his contributions to his retirement plan up to 8% of his salary.
For planning purposes, Rodriguez assumes he will work at American River until he is 60 and believes he can earn 8% per year in a global stock fund. Assume the contributions continue at the same level as in Exercise 1 and estimate the future value.
www.arc.losrios.edu
Facts:
• 1955: Founded
• 2010: About 35,000 students
• 2011: 58% of the students are under 30
• 2011: 50.3% of students are women
American River offers students a choice of more than 70 different majors of study, including biology, engineering, hospitality management, mortuary science, collision repair, business, and even fire technology. College personnel work closely with students to help them find financial aid.
Amazingly, about one-half of the students at American River College receive some kind of financial aid. Roman Rodriguez had 3 years of experience when he went to work in Human Resources at American River College at a salary of $42,000. He began work on his 30th birthday. The college matches his contributions to his retirement plan up to 8% of his salary.
For planning purposes, Rodriguez assumes he will work at American River until he is 60 and believes he can earn 8% per year in a global stock fund. Assume the contributions continue at the same level as in Exercise 1 and estimate the future value.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
24
Find the present value of this annuities.



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
25
Find the amount of this ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples.)
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
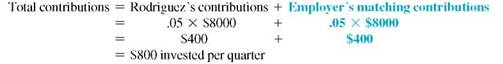
(a) Interest of
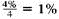 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
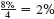 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
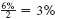 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
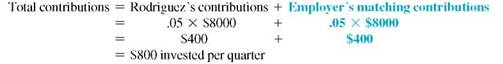
(a) Interest of
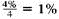 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407. Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
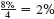 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703. Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
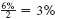 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
26
Solve the following application problems.
MUTUAL FUND INVESTING Sandra Gonzales deposits $1000 into a mutual fund containing international stocks at the end of each semiannual period for 12 years. Assume the fund earns 10% interest compounded semiannually and find the future value. ____________
MUTUAL FUND INVESTING Sandra Gonzales deposits $1000 into a mutual fund containing international stocks at the end of each semiannual period for 12 years. Assume the fund earns 10% interest compounded semiannually and find the future value. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
27
Solve this application problems. Round to the nearest cent.
SELLING A RESTAURANT Anna Stanley has two offers for her pizza business. The first (a) offer is a cash payment of $85,000, and the second is a down payment of $25,000 with (b) payments of $3500 at the end of each quarter for 5 years. (a) Identify the better offer assuming 8% compounded quarterly. ____________ (b) Find the difference in the present values. ____________
SELLING A RESTAURANT Anna Stanley has two offers for her pizza business. The first (a) offer is a cash payment of $85,000, and the second is a down payment of $25,000 with (b) payments of $3500 at the end of each quarter for 5 years. (a) Identify the better offer assuming 8% compounded quarterly. ____________ (b) Find the difference in the present values. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
28
Find the amount of the payment needed to accumulate the indicated amount in a sinking fund. Round to the nearest cent. (See Examples.)
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
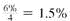 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.
$7894, money earns 12% compounded monthly, 3 years____________
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
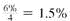 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.

$7894, money earns 12% compounded monthly, 3 years____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the application problem. Round to the nearest cent.
A NEW SHOWROOM A Ford dealership wants to build a new showroom costing $2,300,000. It sets up a sinking fund with end-of-the-month payments in an account earning 12, compounded monthly. Find the amount that should be deposited in this fund each month if the dealership wishes to build the showroom in (a) 3 years ____________and (b) 4 years. ____________
A NEW SHOWROOM A Ford dealership wants to build a new showroom costing $2,300,000. It sets up a sinking fund with end-of-the-month payments in an account earning 12, compounded monthly. Find the amount that should be deposited in this fund each month if the dealership wishes to build the showroom in (a) 3 years ____________and (b) 4 years. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
30
Find the following from the stock table on pages 465 and 466. (See Example 1.)
PE ratio for BlackRock (BLK)____________
PE ratio for BlackRock (BLK)____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
31
Ignore commissions and find the cost for the following stock purchases at the closing price for the week. Then find the annual dividend that will be paid on those shares.
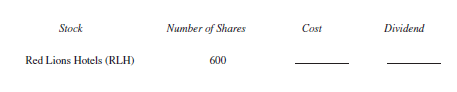
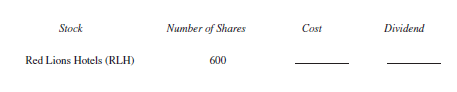

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
32
Stock prices on consecutive days for a stock are shown next. Find the increase (decrease) in the price of each stock as a number and the percent increase (decrease) rounded to the nearest tenth of a percent.
$34.35, 35.20
$34.35, 35.20

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
33
Find the cost, including sales charges of $10 per bond, for each of the following purchases. (See Example 3.)
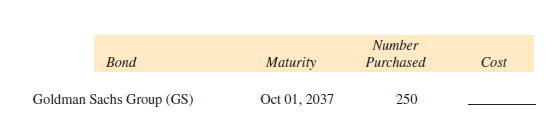
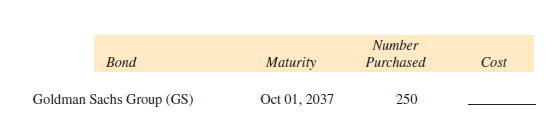

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
34
To help you review, the numbers in brackets show the section in which the topic was discussed.
Find the amounts of the following annuities
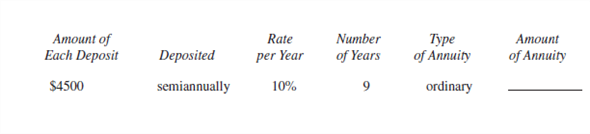
Find the amounts of the following annuities
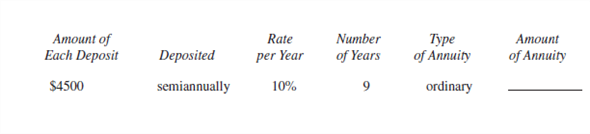

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
35
Find the present value of this annuities.



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
36
Find the amount of this ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples.)
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
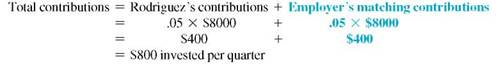
(a) Interest of
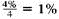 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
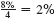 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
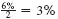 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
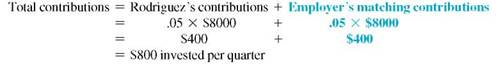
(a) Interest of
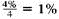 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407. Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
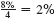 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703. Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
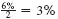 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the following application problems.
T-BILL AND STOCK INVESTING Joann Gretz (see Example, page) decides to place half of her $2000 deposit at the end of each year into the bond fund and half into the stock fund. Assume the bond fund earns 6% compounded annually and the stock fund earns 10% compounded annually. Find the amount available in 33 years. ____________
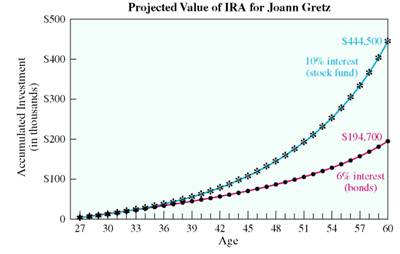
Finding the Value of an IRA
At 27, Joann Gretz sets up an IRA with online broker Charles Schwab, where she plans to deposit $2000 at the end of each year until age 60. Find the amount of the annuity if she invests in (a) a bond fund that has historically yielded 6% compounded annually versus (b) a stock fund that has historically yielded 10% compounded annually. Assume that future yields equal historical yields.
SOLUTION
Age 60 is 60 ? 27 = 33 years away , so she will make deposits at the end of each year for 33 years.
(a) Bond fund: Look down the left column of the amount of an annuity table on page for 33 years and across the top for 6% to find 97.34316.
Amount = $2000 × 97.34316 = $194,686.32
(b) Stock fund: Look down the left column of the table for 33 years and across the top for 10, to find 222.25154.
Amount = $2000 × 222.25154 = $ 444,503.08
Quick TIP
Investments can be risky. For example, stocks usually increase in value over the long term, but they may go down as well.
The differences in the two investments are shown in the figure. Gretz wants the larger amount, but she is worried she might lose money in the stock fund. See Exercise 20 at the end of this section to find her investment choice.
T-BILL AND STOCK INVESTING Joann Gretz (see Example, page) decides to place half of her $2000 deposit at the end of each year into the bond fund and half into the stock fund. Assume the bond fund earns 6% compounded annually and the stock fund earns 10% compounded annually. Find the amount available in 33 years. ____________
Finding the Value of an IRA
At 27, Joann Gretz sets up an IRA with online broker Charles Schwab, where she plans to deposit $2000 at the end of each year until age 60. Find the amount of the annuity if she invests in (a) a bond fund that has historically yielded 6% compounded annually versus (b) a stock fund that has historically yielded 10% compounded annually. Assume that future yields equal historical yields.
SOLUTION
Age 60 is 60 ? 27 = 33 years away , so she will make deposits at the end of each year for 33 years.
(a) Bond fund: Look down the left column of the amount of an annuity table on page for 33 years and across the top for 6% to find 97.34316.
Amount = $2000 × 97.34316 = $194,686.32
(b) Stock fund: Look down the left column of the table for 33 years and across the top for 10, to find 222.25154.
Amount = $2000 × 222.25154 = $ 444,503.08
Quick TIP
Investments can be risky. For example, stocks usually increase in value over the long term, but they may go down as well.
The differences in the two investments are shown in the figure. Gretz wants the larger amount, but she is worried she might lose money in the stock fund. See Exercise 20 at the end of this section to find her investment choice.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
38
Solve this application problems. Round to the nearest cent.
GROCERY STORE Adolf Hegman has two offers for his Canadian grocery company. The first offer is a cash payment of $540,000, and the second is a down payment of $240,000 with payments of $65,000 at the end of each semiannual period for 4 years. (a) Identify the better offer assuming 10% compounded semiannually. ____________ (b) Find the difference in the present values. ____________
GROCERY STORE Adolf Hegman has two offers for his Canadian grocery company. The first offer is a cash payment of $540,000, and the second is a down payment of $240,000 with payments of $65,000 at the end of each semiannual period for 4 years. (a) Identify the better offer assuming 10% compounded semiannually. ____________ (b) Find the difference in the present values. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
39
Solve this application problems. Round to the nearest cent.
Katherine Wysong was injured when she fell on ice at work. Her employer's workers compensation insurance paid for her medical bills and must also pay her $5000 per quarter for the next 6 years. Find the lump sum that must be deposited into an investment earning 4% per year compounded quarterly needed to make the payments. ____________

Katherine Wysong was injured when she fell on ice at work. Her employer's workers compensation insurance paid for her medical bills and must also pay her $5000 per quarter for the next 6 years. Find the lump sum that must be deposited into an investment earning 4% per year compounded quarterly needed to make the payments. ____________


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the application problem. Round to the nearest cent.
AIRPORT IMPROVEMENTS A city near Chicago sold $9,000,000 in bonds to pay for improvements to an airport. It sets up a sinking fund with end-of-the-quarter payments in an account earning 8, compounded quarterly. Find the amount that should be deposited in this fund each quarter if the city wishes to pay off the bonds in (a) 7 years ____________and (b) 12 years. ____________
AIRPORT IMPROVEMENTS A city near Chicago sold $9,000,000 in bonds to pay for improvements to an airport. It sets up a sinking fund with end-of-the-quarter payments in an account earning 8, compounded quarterly. Find the amount that should be deposited in this fund each quarter if the city wishes to pay off the bonds in (a) 7 years ____________and (b) 12 years. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
41
Find the following from the stock table on pages 465 and 466. (See Example 1.)
PE ratio for Baytex Energy Trust (BTE)____________
PE ratio for Baytex Energy Trust (BTE)____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
42
Ignore commissions and find the cost for the following stock purchases at the closing price for the week. Then find the annual dividend that will be paid on those shares.
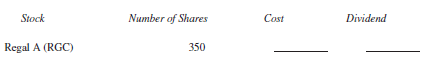
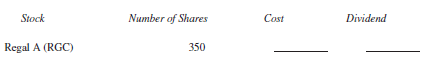

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
43
Stock prices on consecutive days for a stock are shown next. Find the increase (decrease) in the price of each stock as a number and the percent increase (decrease) rounded to the nearest tenth of a percent.
$46.50, 45.90
$46.50, 45.90

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
44
Find the cost, including sales charges of $10 per bond, for each of the following purchases. (See Example 3.)
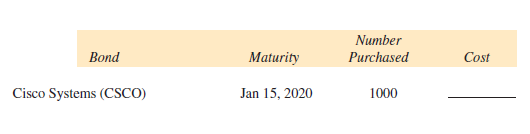
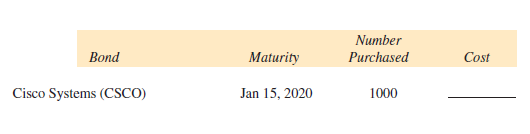

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
45
Li has read newspaper articles stating that Social Security benefits will be reduced in the years ahead. After some thought, he decides to be conservative and assume that Social Security will pay only the first $30,000 of the annual income he needs at age 67. Find the remaining income he will need beginning at age 67. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
46
Betty Yowski borrows money for a new swimming pool and hot tub. She agrees to repay the note with a payment of $1200 per quarter for 6 years. Find the amount she must set aside today to satisfy this capital requirement in an investment earning 8% compounded quarterly. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
47
Find the amount of this ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples.)
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
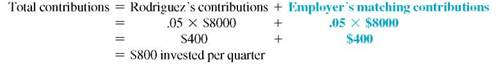
(a) Interest of
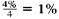 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
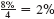 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
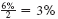 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.

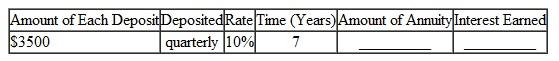
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
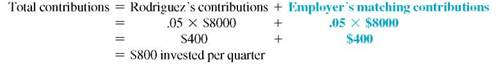
(a) Interest of
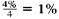 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407. Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
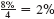 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703. Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
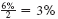 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
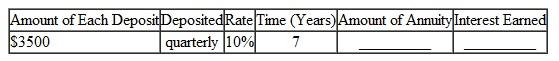

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
48
Find the present value of the following annuities. Round to the nearest cent. (See Examples 1-3.)
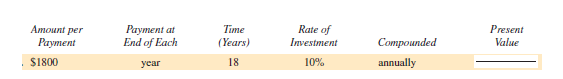
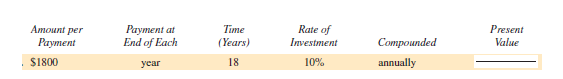

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the following application problems. Round to the nearest cent.
SOCIAL SECURITY Jessica Thames expects to receive $18,400 per year based on her deceased husband's contributions to Social Security. Assume that she receives payments for 14 years and a rate of 8% per year, and find the present value of this annuity.
SOCIAL SECURITY Jessica Thames expects to receive $18,400 per year based on her deceased husband's contributions to Social Security. Assume that she receives payments for 14 years and a rate of 8% per year, and find the present value of this annuity.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
50
Find the amount of the payment needed to accumulate the indicated amount in a sinking fund. Round to the nearest cent. (See Examples.)
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
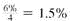 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.
$29,804, money earns 12% compounded monthly, 2 years____________
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
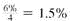 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)

Finding the Periodic Payments
First Christian Church sold $100,000 worth of bonds that must be paid off in 8 years. It now must set up a sinking fund to accumulate the necessary $100,000 to pay off the debt. Find the amount of each payment into a sinking fund if the payments are made at the end of each year and the fund earns 10% compounded annually. Find the amount of interest earned.
SOLUTION
Look along the top of the sinking fund table for 10% and down the side for 8 periods to find.08744.
Payment = $100,000 ×.08744 = $ 8744
The church must deposit $8744 at the end of each year for 8 years into an account paying 10% compounded annually to accumulate $100,000. The interest earned is the future value less all payments.
Interest = $100,000 ? (8 × $8744) = $ 30,048

Setting up a Sinking Fund Table
First Christian Church in Example deposited $8744 at the end of each year for 8 years into a sinking fund that earned 10% compounded annually. Set up a sinking fund table for these deposits. After each calculation, round each answer to the nearest cent before proceeding.
SOLUTION
The sinking fund account contains no money until the end of the first year, when a single deposit of $8744 is made. Since the deposit is made at the end of the year, no interest is earned.
At the end of the second year, the account contains the original $8744 plus the interest earned by this money. This interest is found by the formula for simple interest.
I = $8744 ×.10 × 1 = $874.40
An additional deposit is also made at the end of the second year, so that the sinking fund then contains the following total.
$8744 + $874.40 + $8744 = $18,362.40
Continue this work to get the following sinking fund table.
Quick TIP
Normally the last payment is adjusted as needed so that the future value exactly equals the desired amount. We assume this is true from this point forward.

$29,804, money earns 12% compounded monthly, 2 years____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the application problem. Round to the nearest cent.
LAND SALE Helen Spence sells a lot in Nevada. She will be paid a lump sum of $60,000 in 4 years. Until then, the buyer pays 8% simple interest every quarter. (a) Find the amount of each quarterly interest payment. ____________ (b) The buyer sets up a sinking fund so that enough money will be present to pay off the $60,000. The buyer wants to make semiannual payments into the sinking fund. The account pays 8% compounded semiannually. Find the amount of each payment into the fund. ____________ (c) Prepare a table showing the amount in the sinking fund after each deposit.

LAND SALE Helen Spence sells a lot in Nevada. She will be paid a lump sum of $60,000 in 4 years. Until then, the buyer pays 8% simple interest every quarter. (a) Find the amount of each quarterly interest payment. ____________ (b) The buyer sets up a sinking fund so that enough money will be present to pay off the $60,000. The buyer wants to make semiannual payments into the sinking fund. The account pays 8% compounded semiannually. Find the amount of each payment into the fund. ____________ (c) Prepare a table showing the amount in the sinking fund after each deposit.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
52
Find the following from the stock table on pages 465 and 466. (See Example 1.)
Estimated earnings per share for this year for Barck Gold (ABX) ____________
Estimated earnings per share for this year for Barck Gold (ABX) ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
53
Define and explain (a) current yield and (b) PE ratio.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the following application problems.
STOCK PURCHASE Patsy Bonner buys 200 shares of Target at $56.30 and 100 shares of Pepsi at $38.60. Find the total cost ignoring commissions.
STOCK PURCHASE Patsy Bonner buys 200 shares of Target at $56.30 and 100 shares of Pepsi at $38.60. Find the total cost ignoring commissions.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
55
Explain the purpose of bonds. (See Objective.)

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
56
AMERICAN RIVER COLLEGE
www.arc.losrios.edu
Facts:
• 1955: Founded
• 2010: About 35,000 students
• 2011: 58% of the students are under 30
• 2011: 50.3% of students are women
American River offers students a choice of more than 70 different majors of study, including biology, engineering, hospitality management, mortuary science, collision repair, business, and even fire technology. College personnel work closely with students to help them find financial aid.
Amazingly, about one-half of the students at American River College receive some kind of financial aid. Roman Rodriguez had 3 years of experience when he went to work in Human Resources at American River College at a salary of $42,000. He began work on his 30th birthday. The college matches his contributions to his retirement plan up to 8% of his salary.
Assume that there are 422 full-time faculty at American River College and that their average income is $48,500 per year. Find the annual payroll for the faculty.
www.arc.losrios.edu
Facts:
• 1955: Founded
• 2010: About 35,000 students
• 2011: 58% of the students are under 30
• 2011: 50.3% of students are women
American River offers students a choice of more than 70 different majors of study, including biology, engineering, hospitality management, mortuary science, collision repair, business, and even fire technology. College personnel work closely with students to help them find financial aid.
Amazingly, about one-half of the students at American River College receive some kind of financial aid. Roman Rodriguez had 3 years of experience when he went to work in Human Resources at American River College at a salary of $42,000. He began work on his 30th birthday. The college matches his contributions to his retirement plan up to 8% of his salary.
Assume that there are 422 full-time faculty at American River College and that their average income is $48,500 per year. Find the annual payroll for the faculty.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
57
Dan and Mary Foster just divorced. The divorce settlement included $650 a month payment to Dan for the 4 years until their son turns 18. Find the amount Mary must set aside today in an account earning 12, per year compounded monthly to satisfy this financial obligation.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
58
Find the amount of this ordinary annuities rounded to the nearest cent. Find the total interest earned. (See Examples.)
Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
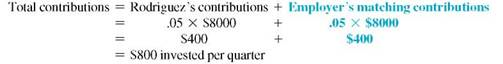
(a) Interest of
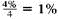 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
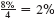 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
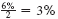 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Finding the Value of an Annuity and Interest Earned
Roman Rodriguez's employer will match his contributions into a retirement plan up to 5% of his $32,000 annual salary. In other words, the employer will put $1 into his retirement plan for every $1 Rodriguez puts into his retirement plan up to the limit. Find the future amount in 8 years if every quarter he contributes the maximum allowed assuming (a) funds earn 4% compounded quarterly and (b) funds earn 8% compounded quarterly. (c) Then find the difference between the two.
CASE IN POINT
SOLUTION
Salary per quater = $32,000 ÷ 4 = $8000
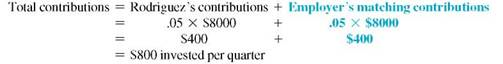
(a) Interest of
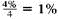 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 1% and down the side for 32 periods to find 37.49407. Amount = $800 × 37.49407 = $29,995.26 (rounded)
(b) Interest of
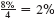 is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703.
is earned per quarter for 8 × 4 = 32 quarters. Look across the top of the table for 2% and down the side for 32 periods to find 44.22703. Amount = $800 × 44.22703 = $35,381.62 (rounded)
(c) Difference = $35,381.62 ? $30,295.21 = $5086.41
Finding the Amount of an Annuity and Interest Earned

At the birth of her grandson, Junella Smith commits to help pay for his college education. She decides to make deposits of $600 at the end of each 6 months into an account for 17 years. Find the amount of the annuity and the interest earned, assuming 6% compounded semiannually.
SOLUTION
Interest of
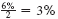 is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.
is earned each semiannual period. There are 17 × 2 = 34 semiannual periods in 17 years. Find 3% across the top and 34 periods down the side of the table for 57.73018.Amount = $600 × 57.73018 = $ 34,638.11
Interest = $34,638.11 ? ( 34 × $600) = $14,238.11 (rounded)
Smith knows that a college education will cost a lot more in 17 years than it does now, but she also knows that $34,638.11 will be of great help to her grandson.
Financial Calculator solution
In this example, payment ($600), interest rate per compounding period (3,), and number of compounding periods (34) are known. Future value is the unknown. Enter the payment as a negative number since it is an outflow of cash that Junella Smith pays each month. Finally, press the
 key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.
key to find the future value, which is a positive value since it will be an inflow of cash to her grandson.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
59
Find the present value of the following annuities. Round to the nearest cent. (See Examples 1-3.)
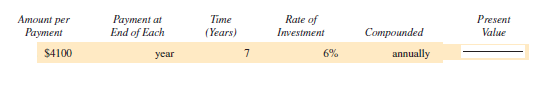
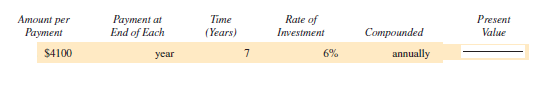

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
60
Solve this application problems. Round to the nearest cent.
SOCIAL SECURITY Warren and Bernice White's combined Social Security payments add up to $35,400 per year. Assume payments for 20 years and a rate of 6% per year, and find the present value. ____________
SOCIAL SECURITY Warren and Bernice White's combined Social Security payments add up to $35,400 per year. Assume payments for 20 years and a rate of 6% per year, and find the present value. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
61
Solve this application problems. Round to the nearest cent.
Carl and Amy Glaser recently divorced. As part of the divorce settlement, Carl must pay Amy $1000 at the end of every quarter for 8 years. Find the lump sum he must deposit into an account earning 8% per year compounded quarterly to make the payments. ____________
Carl and Amy Glaser recently divorced. As part of the divorce settlement, Carl must pay Amy $1000 at the end of every quarter for 8 years. Find the lump sum he must deposit into an account earning 8% per year compounded quarterly to make the payments. ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the application problem. Round to the nearest cent.
RARE STAMPS Jeff Reschke bought a rare stamp for his collection. He agreed to pay a lump sum of $4000 after 5 years. Until then, he pays 6% simple interest every 6 months. (a) Find the amount of each semiannual interest payment. ____________ (b) Reschke sets up a sinking fund so that money will be available to pay off the $4000. He wants to make annual payments into the fund. The account pays 8% compounded annually. Find the amount of each payment into the fund. ____________ (c) Prepare a table showing the amount in the sinking fund after each deposit.

RARE STAMPS Jeff Reschke bought a rare stamp for his collection. He agreed to pay a lump sum of $4000 after 5 years. Until then, he pays 6% simple interest every 6 months. (a) Find the amount of each semiannual interest payment. ____________ (b) Reschke sets up a sinking fund so that money will be available to pay off the $4000. He wants to make annual payments into the fund. The account pays 8% compounded annually. Find the amount of each payment into the fund. ____________ (c) Prepare a table showing the amount in the sinking fund after each deposit.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
63
Find the following from the stock table on pages 465 and 466. (See Example 1.)
Estimated earnings per share for this year for Bank Hawaii (BOH)_____________
Estimated earnings per share for this year for Bank Hawaii (BOH)_____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
64
Use the chart of the Dow Jones Industrial Average and estimate the years in which stocks fell by more than 10%. (See Objective 5.)
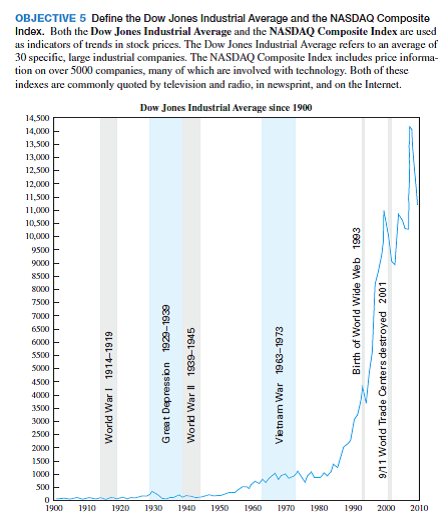


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the following application problems.
WRITING A WILL In her will, Barbara Bains stated that the trustee should purchase 300 shares of McDonalds and 200 shares of Wal-Mart and give the stock to her grandson on his 25th birthday. If the stocks are selling for $58.70 per share and $52.20 per share, respectively, find the total amount paid, ignoring broker's commissions.
WRITING A WILL In her will, Barbara Bains stated that the trustee should purchase 300 shares of McDonalds and 200 shares of Wal-Mart and give the stock to her grandson on his 25th birthday. If the stocks are selling for $58.70 per share and $52.20 per share, respectively, find the total amount paid, ignoring broker's commissions.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
66
Explain how a bondholder can estimate the effective interest rate return on the total cost of the investment, including commissions. (See Example.)
Finding the Cost to Buy Bonds
Assume that the sales charge is $1 per bond, and find the following for Morgan Stanley (MS) bonds maturing in 2042.
(a) The total cost of purchasing 20 bonds
(b) The total annual interest paid on these bonds
(c) The effective interest rate to the buyer including the cost of buying the bonds
SOLUTION

Finding the Cost to Buy Bonds
Assume that the sales charge is $1 per bond, and find the following for Morgan Stanley (MS) bonds maturing in 2042.
(a) The total cost of purchasing 20 bonds
(b) The total annual interest paid on these bonds
(c) The effective interest rate to the buyer including the cost of buying the bonds
SOLUTION


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
67
To help you review, the numbers in brackets show the section in which the topic was discussed.
Find the amounts of this annuities.

Find the amounts of this annuities.


Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
68
Find the amount of each payment into a sinking fund for the following.



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
69
Find the amount of the following annuities due rounded to the nearest cent. Find the total interest earned. (See Example 3.)
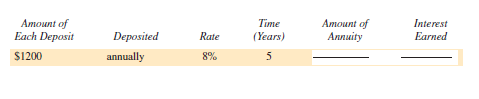
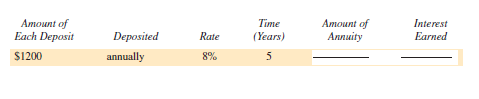

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
70
Find the present value of this annuities. Round to the nearest cent. (See Examples.)
Finding the Present Value of an Annuity
At the end of each quarter for 5 years, the Daily News deposits $4325 in an account paying 6% compounded quarterly. The goal is to accumulate funds for a new printing press. ( a ) Use the concepts of Section to find the future value of the annuity. ( b ) Then find the lump sum (present value) that must be deposited today to accumulate the same future value.
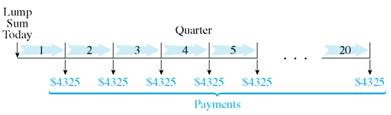
SOLUTION
(a)
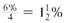 (or 1.5%) per quarter; 5 years × 4 = 20 quarters. Use the amount of an annuity table in Section to find 23.12367.
(or 1.5%) per quarter; 5 years × 4 = 20 quarters. Use the amount of an annuity table in Section to find 23.12367.
Future value = $4325 × 23.12367 = $ 100,009.87 (rounded)
(b) It is not necessary to use this future value to find the present value of the annuity. Instead, use the present value of an annuity table with 1.5, per period and 20 periods to find 17.16864.
Present value = $4325 × 17.16864 = $74,254.37
Thus, a deposit of $4325 at the end of every quarter for 5 years has a present value today of $74,254.37. If we assume 6% compounded quarterly and ignore income taxes, each of the following has exactly the same value:
1. 20 end-of-quarter deposits of $4325
2. A future value at the end of 5 years of $100,009.87
3. A present value on hand today of $74,254.37
Finding the Present Value
Tom and Brandy Barrett recently divorced. The judge gave custody of their 4-year-old son to Brandy and ruled that Tom must pay $1500 in child support to Brandy at the end of each quarter until the son turns 16. Find the lump sum that Tom must put into an account earning 6% compounded quarterly to cover the periodic payments. Find the interest earned.
SOLUTION
Payments must be made for 16 - 4 = 12 years, or for 12 × 4 = 48 quarters. The interest rate per quarter is
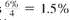 per quarter. Look across the top of the present value of an annuity table for 1.5% and down the side for 48 payments to find 34.04255.
per quarter. Look across the top of the present value of an annuity table for 1.5% and down the side for 48 payments to find 34.04255.
Present value of annuity = $1500 × 34.04255 = $ 51,063.83
A deposit of $51,063.83 today will make 48 end-of-quarter payments of $1500 each. Interest earned during the 12 years is the sum of all payments less the original lump sum.
Interest = (48 × $1500) - $51,063.83 = $20,936.17
Quick TIP
Although the $1500 withdrawals to Brandy are at the end of each quarter, the original lump sum must be deposited at the beginning of the first year.
Finding the Present Value
An American company hires a project manager to work in Saudi Arabia. The contract states that if the manager works there for 5 years, he will receive an extra benefit of $15,000 at the end of each semiannual period for the 8 years that follow. Find the lump sum that can be deposited today to satisfy the contract, assuming 6% compounded semiannually.
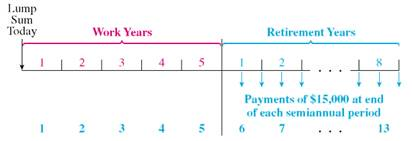
SOLUTION
The project manager works from years 1 to 5. He then receives two $15,000 annuity payments each year during years 6 through 13. Solve this problem in two steps.
1. Find the present value at the beginning of year 6 of the annuity with $15,000 payments.
Use
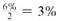 per compounding period and 8 × 2 = 16 compounding periods to find 12.56110 in the present value of an annuity table.
per compounding period and 8 × 2 = 16 compounding periods to find 12.56110 in the present value of an annuity table.
Present value of annuity = $15,000 × 12.56110 = $188,416.50
This is the present value of the annuity needed at the beginning of year 6 to fund payments in years 6 through 13. But it is also the future value needed for the investment made today that will fund the eventual payments.
2. Find the lump sum needed today to accumulate the $188,416.50 by the end of year 5.
Use the table showing present value of a dollar in Section (page) with
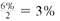 per compounding period and 5 × 2 = 10 compounding periods to find.74409.
per compounding period and 5 × 2 = 10 compounding periods to find.74409.
Present value needed today = $188,416.50 ×.74409 = $ 140,198.83
A lump sum of $140,198.83 today will grow to $188,416.50 in 5 years. The $188,416.50 at the end of year 5 is enough to make 16 semiannual payments of $15,000 each during years 6 through 13.
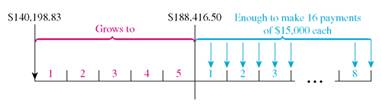
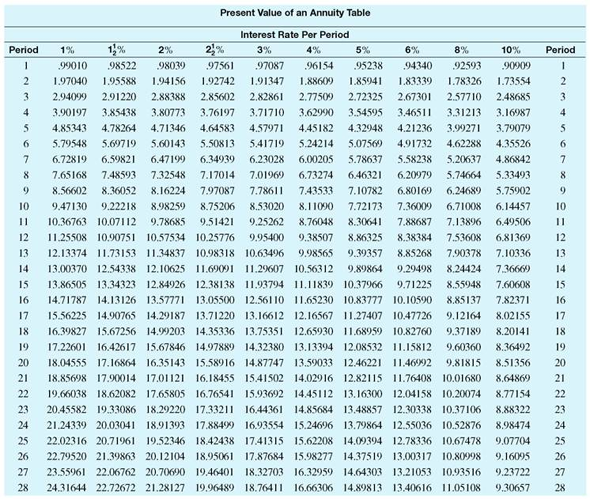
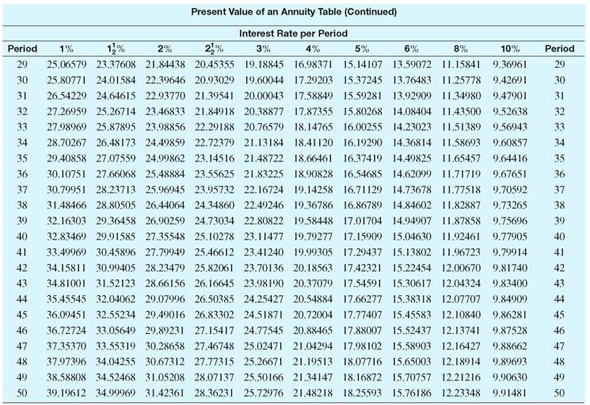
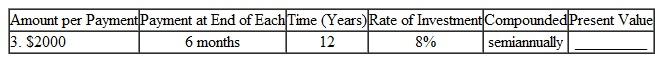
Finding the Present Value of an Annuity
At the end of each quarter for 5 years, the Daily News deposits $4325 in an account paying 6% compounded quarterly. The goal is to accumulate funds for a new printing press. ( a ) Use the concepts of Section to find the future value of the annuity. ( b ) Then find the lump sum (present value) that must be deposited today to accumulate the same future value.

SOLUTION
(a)
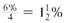 (or 1.5%) per quarter; 5 years × 4 = 20 quarters. Use the amount of an annuity table in Section to find 23.12367.
(or 1.5%) per quarter; 5 years × 4 = 20 quarters. Use the amount of an annuity table in Section to find 23.12367.Future value = $4325 × 23.12367 = $ 100,009.87 (rounded)
(b) It is not necessary to use this future value to find the present value of the annuity. Instead, use the present value of an annuity table with 1.5, per period and 20 periods to find 17.16864.
Present value = $4325 × 17.16864 = $74,254.37
Thus, a deposit of $4325 at the end of every quarter for 5 years has a present value today of $74,254.37. If we assume 6% compounded quarterly and ignore income taxes, each of the following has exactly the same value:
1. 20 end-of-quarter deposits of $4325
2. A future value at the end of 5 years of $100,009.87
3. A present value on hand today of $74,254.37
Finding the Present Value
Tom and Brandy Barrett recently divorced. The judge gave custody of their 4-year-old son to Brandy and ruled that Tom must pay $1500 in child support to Brandy at the end of each quarter until the son turns 16. Find the lump sum that Tom must put into an account earning 6% compounded quarterly to cover the periodic payments. Find the interest earned.
SOLUTION
Payments must be made for 16 - 4 = 12 years, or for 12 × 4 = 48 quarters. The interest rate per quarter is
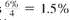 per quarter. Look across the top of the present value of an annuity table for 1.5% and down the side for 48 payments to find 34.04255.
per quarter. Look across the top of the present value of an annuity table for 1.5% and down the side for 48 payments to find 34.04255.Present value of annuity = $1500 × 34.04255 = $ 51,063.83
A deposit of $51,063.83 today will make 48 end-of-quarter payments of $1500 each. Interest earned during the 12 years is the sum of all payments less the original lump sum.
Interest = (48 × $1500) - $51,063.83 = $20,936.17
Quick TIP
Although the $1500 withdrawals to Brandy are at the end of each quarter, the original lump sum must be deposited at the beginning of the first year.
Finding the Present Value
An American company hires a project manager to work in Saudi Arabia. The contract states that if the manager works there for 5 years, he will receive an extra benefit of $15,000 at the end of each semiannual period for the 8 years that follow. Find the lump sum that can be deposited today to satisfy the contract, assuming 6% compounded semiannually.

SOLUTION
The project manager works from years 1 to 5. He then receives two $15,000 annuity payments each year during years 6 through 13. Solve this problem in two steps.
1. Find the present value at the beginning of year 6 of the annuity with $15,000 payments.
Use
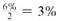 per compounding period and 8 × 2 = 16 compounding periods to find 12.56110 in the present value of an annuity table.
per compounding period and 8 × 2 = 16 compounding periods to find 12.56110 in the present value of an annuity table.Present value of annuity = $15,000 × 12.56110 = $188,416.50
This is the present value of the annuity needed at the beginning of year 6 to fund payments in years 6 through 13. But it is also the future value needed for the investment made today that will fund the eventual payments.
2. Find the lump sum needed today to accumulate the $188,416.50 by the end of year 5.
Use the table showing present value of a dollar in Section (page) with
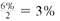 per compounding period and 5 × 2 = 10 compounding periods to find.74409.
per compounding period and 5 × 2 = 10 compounding periods to find.74409.Present value needed today = $188,416.50 ×.74409 = $ 140,198.83
A lump sum of $140,198.83 today will grow to $188,416.50 in 5 years. The $188,416.50 at the end of year 5 is enough to make 16 semiannual payments of $15,000 each during years 6 through 13.



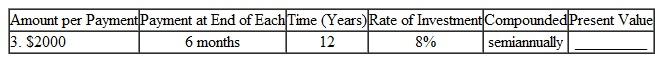

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
71
Find the amount of each payment needed to accumulate the indicated amount in a sinking fund. Round to the nearest cent. (See Examples 1-3.)
$12,000, money earns 5% compounded annually, 4 years__________
$12,000, money earns 5% compounded annually, 4 years__________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
72
Explain the difference between a sinking fund (see OBJECTIVE) and the present value of an annuity discussed in Section.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the application problem. Round to the nearest cent.
SPORTS COMPLEX Prepare a sinking fund table for the first four payments for the community college sports complex described in Example.
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
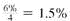 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)


SPORTS COMPLEX Prepare a sinking fund table for the first four payments for the community college sports complex described in Example.
Finding Periodic Payments
Administrators at a community college have decided to build, in 5 years, a new sports complex with two indoor 50-meter swimming pools and a large gymnasium. The cost estimate is $16,500,000. They decide to make end-of-quarter deposits into a fund expected to earn 6% compounded quarterly. Find ( a ) the amount of each quarterly payment and ( b ) the interest earned.
CASE IN POINT
SOLUTION
(a) Use
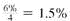 per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.
per compounding period for 5 × 4 years = 20 compounding periods in the sinking fund table on page to find.04325.Quarterly payment = $16,500,000 ×.04325 = $713,625
Twenty end-of-quarter payments of $713,625 at 6% compounded quarterly will grow to $16,501,629 using the table in Section.
(b) Interest is the future value minus the payments.
Interest = $16,501,629 ? 120 × $713,6252 = $ 2,229,129 (rounded)



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
74
Find the following from the stock table on pages 465 and 466. (See Example 1.)
Dividend yield for Realty Inco (O)____________
Dividend yield for Realty Inco (O)____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
75
Find the current yield for each of the following stocks. Round to the nearest tenth of a percent. (See Example 3.)
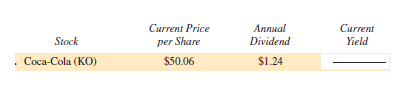
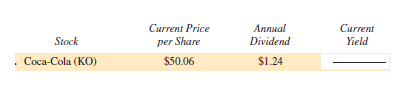

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the following application problems.
CDS OR GLOBAL STOCKS Stan Walker is comparing treasury bills currently yielding 5% compounded semiannually to a mutual fund with stocks that he believes will yield 8% compounded semiannually. Find the future value of an annuity with deposits of $600 every 6 months for 10 years for (a) the CDs and (b) the mutual fund. (c) Find the difference.
CDS OR GLOBAL STOCKS Stan Walker is comparing treasury bills currently yielding 5% compounded semiannually to a mutual fund with stocks that he believes will yield 8% compounded semiannually. Find the future value of an annuity with deposits of $600 every 6 months for 10 years for (a) the CDs and (b) the mutual fund. (c) Find the difference.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
77
Solve each application problem. Assume a sales commission of $10 per bond, unless indicated otherwise, and use the table in this section. Round the rate to the nearest tenth of a percent.
BOND FUND Pete Chong manages bonds for a fund company. He purchases 4000 Goldman Sachs Group (GS) bonds that mature in 2037. Since this is a large purchase, the commission is only $.80 per bond. Find (a) the total cost of the purchase including commissions, (b) the annual interest payment, and (c) the effective interest rate based on total cost including commissions.
BOND FUND Pete Chong manages bonds for a fund company. He purchases 4000 Goldman Sachs Group (GS) bonds that mature in 2037. Since this is a large purchase, the commission is only $.80 per bond. Find (a) the total cost of the purchase including commissions, (b) the annual interest payment, and (c) the effective interest rate based on total cost including commissions.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
78
Li decides to plan funding for his retirement for 20 years, from ages 67 to 87. If funds earn 8% compounded annually, find the present value of the annual income that he needs at 67 based on the income from part (c). ____________

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
79
Find the amount of each payment into a sinking fund for the following.



Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
80
the amount of the following annuities due rounded to the nearest cent. Find the total interest earned. (See Example 3.)
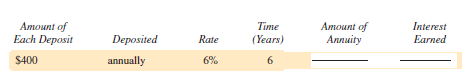
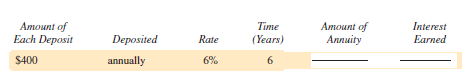

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck


