Deck 12: Business and Consumer Loans
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/168
Play
Full screen (f)
Deck 12: Business and Consumer Loans
1
Round money amounts to the nearest cent and rates to the nearest tenth of a percent.
Find the amount and interest earned of each of the following ordinary annuities.

Find the amount and interest earned of each of the following ordinary annuities.

This is a problem of finding the amount of an annuity.
The following table is given,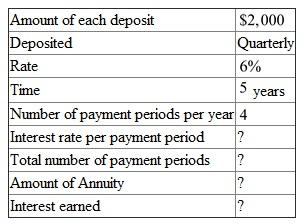 There are
There are 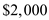 payment periods.
payment periods.
The interest rate per payment period is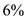 .
.
Look across the top of the Amount of an Annuity Table for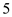 and down the side for
and down the side for 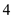 periods to find
periods to find 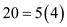 .
.
Recall the formula, Finding Amount of an Annuity,
"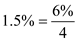 , or
, or 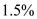 "
"
Use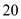 , and
, and 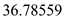 in the formula above,
in the formula above, 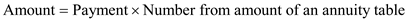 Therefore, the amount of annuity is
Therefore, the amount of annuity is 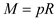 .
.
Recall the formula, Finding Interest of an Annuity,
"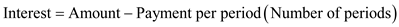 , or
, or 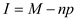 "
"
Use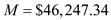 ,
, 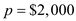 , and
, and 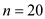 in the formula above,
in the formula above, 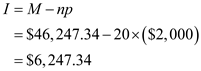 Therefore, the interest earned is
Therefore, the interest earned is 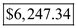 .
.
The following table is given,
 There are
There are 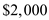 payment periods.
payment periods. The interest rate per payment period is
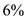 .
. Look across the top of the Amount of an Annuity Table for
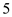 and down the side for
and down the side for 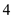 periods to find
periods to find 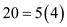 .
. Recall the formula, Finding Amount of an Annuity,
"
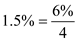 , or
, or 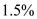 "
"Use
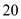 , and
, and 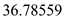 in the formula above,
in the formula above, 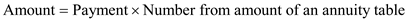 Therefore, the amount of annuity is
Therefore, the amount of annuity is 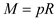 .
.Recall the formula, Finding Interest of an Annuity,
"
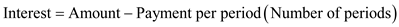 , or
, or 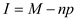 "
"Use
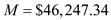 ,
, 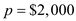 , and
, and 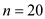 in the formula above,
in the formula above, 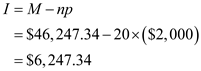 Therefore, the interest earned is
Therefore, the interest earned is 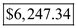 .
. 2
Solve the following application problems.
A note with a face value of $7000 is made on June 21. The note is for 90 days and carries interest of 13%. A partial payment of $2800 is made on July 17. Find the amount due on the maturity date of the note. __________ [12.3]
A note with a face value of $7000 is made on June 21. The note is for 90 days and carries interest of 13%. A partial payment of $2800 is made on July 17. Find the amount due on the maturity date of the note. __________ [12.3]
There are 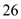 days from June 21 to July 17:
days from June 21 to July 17: 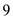 days in June, and
days in June, and 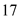 days in July.
days in July.
The following table is given,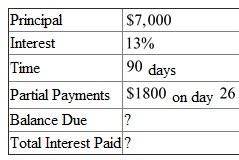 Recall the rule, the United States Rule,
Recall the rule, the United States Rule,
"Step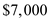 : Find the simple interest due from the date the loan was made until the date the partial payment is made.
: Find the simple interest due from the date the loan was made until the date the partial payment is made.
Step 2: Subtract this interest from the amount of the payment.
Step 3: Any difference is used to reduce the principal.
Step 4: Treat additional partial payments in the same way, always finding interest on only the unpaid balance after the last partial payment.
Step 5: The remaining principal plus interest on this unpaid principal is then due on the due date of the loan."
You are supposed to following the steps one by one.
Step : Find the simple interest due from the date the loan was made until the date the partial payment is made.
: Find the simple interest due from the date the loan was made until the date the partial payment is made.
Recall the formula, Finding Simple Interest,
"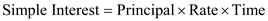
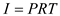 "
"
Use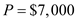 ,
, 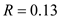 , and
, and 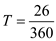 in the formula above,
in the formula above, 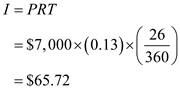 Step 2: Subtract this interest from the amount of the payment.
Step 2: Subtract this interest from the amount of the payment.
The amount of first payment applied to reduce debt is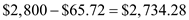 .
.
Step 3: Any difference is used to reduce the principal.
The debt after first payment is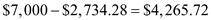 .
.
Step 4: Treat additional partial payments in the same way, always finding interest on only the unpaid balance after the last partial payment.
There are no additional partial payments in this question.
Step 5: The remaining principal plus interest on this unpaid principal is then due on the due date of the loan.
The balance due on maturity date is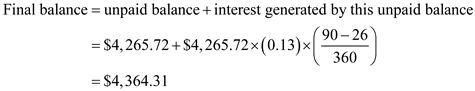 Therefore, the balance due is
Therefore, the balance due is 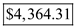 .
.
 days from June 21 to July 17:
days from June 21 to July 17:  days in June, and
days in June, and  days in July.
days in July. The following table is given,
 Recall the rule, the United States Rule,
Recall the rule, the United States Rule, "Step
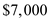 : Find the simple interest due from the date the loan was made until the date the partial payment is made.
: Find the simple interest due from the date the loan was made until the date the partial payment is made. Step 2: Subtract this interest from the amount of the payment.
Step 3: Any difference is used to reduce the principal.
Step 4: Treat additional partial payments in the same way, always finding interest on only the unpaid balance after the last partial payment.
Step 5: The remaining principal plus interest on this unpaid principal is then due on the due date of the loan."
You are supposed to following the steps one by one.
Step
 : Find the simple interest due from the date the loan was made until the date the partial payment is made.
: Find the simple interest due from the date the loan was made until the date the partial payment is made. Recall the formula, Finding Simple Interest,
"
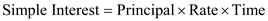
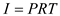 "
"Use
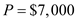 ,
, 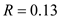 , and
, and 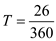 in the formula above,
in the formula above, 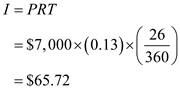 Step 2: Subtract this interest from the amount of the payment.
Step 2: Subtract this interest from the amount of the payment. The amount of first payment applied to reduce debt is
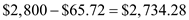 .
. Step 3: Any difference is used to reduce the principal.
The debt after first payment is
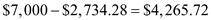 .
. Step 4: Treat additional partial payments in the same way, always finding interest on only the unpaid balance after the last partial payment.
There are no additional partial payments in this question.
Step 5: The remaining principal plus interest on this unpaid principal is then due on the due date of the loan.
The balance due on maturity date is
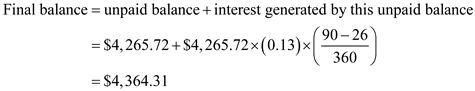 Therefore, the balance due is
Therefore, the balance due is 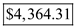 .
. 3
Work the following application problems.
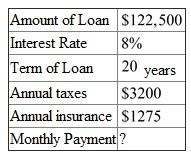
Jerome Watson, owner of Watson Welding, purchases a storage building for his business and makes a $25,000 down payment. He finances the balance of $122,500 for 20 years at 8%. (a) Find the total monthly payment given taxes of $3200 per year and insurance of $1275 per year. ___________ (b) Assume that insurance and taxes do not increase, and find the total cost owning the building for 20 years (including the down payment). ___________
Jerome Watson, owner of Watson Welding, purchases a storage building for his business and makes a $25,000 down payment. He finances the balance of $122,500 for 20 years at 8%. (a) Find the total monthly payment given taxes of $3200 per year and insurance of $1275 per year. ___________ (b) Assume that insurance and taxes do not increase, and find the total cost owning the building for 20 years (including the down payment). ___________
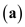 This is a problem of finding the monthly payment for a mortgage.
This is a problem of finding the monthly payment for a mortgage. The following table is given,
 Look across the top of the Real Estate Amortization Table for
Look across the top of the Real Estate Amortization Table for 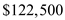 and down the side for
and down the side for  periods to find
periods to find 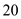 .
. Recall the formula, Finding the Monthly Payment for a Mortgage,
"
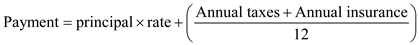 , or
, or 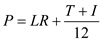 "
"The amount to be financed in thousands is
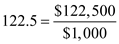 .
. Use
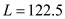 ,
, 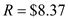 , and
, and 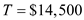 ,
, 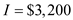 in the formula above,
in the formula above, 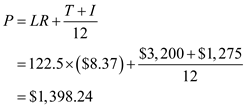 Therefore, the monthly payment is
Therefore, the monthly payment is  .
.  Recall the formula, Finding the Total Installment Cost,
Recall the formula, Finding the Total Installment Cost, "
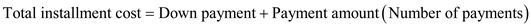 , or
, or 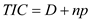 "
"Use
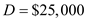 ,
, 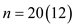 , and
, and 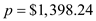 in the formula above,
in the formula above, 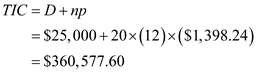 Therefore, the total cost of owning the building for
Therefore, the total cost of owning the building for 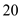 years is
years is 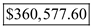 .
. 4
Explain how consolidating loans may be of some advantage to the borrower. What disadvantages can you think of?

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
5
Find the finance charge (FC) and the total installment cost (TIC) for the following. (See Example.)
Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.

Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
6
Explain the difference between open-end credit and installment loans. (See Section and OBJECTIVE of this section.)
Define installment loan. A loan is amortized if both principal and interest are paid off by a sequence of equal periodic payments. This type of loan is called an installment loan. People use installment loans for cars, boats, home improvements, and even for consolidating several loans into one affordable loan. Firms use installment loans to purchase equipment, computers, vehicles, mining equipment, etc. The graphic shows the total interest that must be paid when financing a new Ford Escape over 3, 4, and 5 years. Notice that financing the SUV over 5 years results in interest costs of $2600, thereby increasing the total cost of the $25,000 loan to $27,600 or by 10.4%.

Quick TIP
The interest rates on installments loans can be very high.
Notice that the total interest paid is much higher the longer the term of the loan. It may be difficult to make the higher payments of a short-term loan, but it results in less total interest!
The federal Truth in Lending Act (Regulation Z) of 1969 requires lenders to disclose their finance charge (the charge for credit) and annual percentage rate (APR) on installment loans. The federal government does not regulate rates. Each individual state sets the maximum allowable rates and charges.
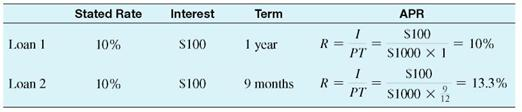
The interest rate that is stated (in the newspaper, a marketing brochure, or a problem in a textbook) is also called the nominal rate. The nominal or stated rate can differ from the annual percentage rate or APR, which is based on the actual amount received by the borrower. The APR is the true effective annual interest rate for a loan. Information on two loans of $1000 each is shown below. An advertisement indicates a rate of 10, for each loan, and the actual interest is $100 for each. However, the terms differ as do the APRs.
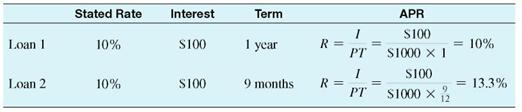
The interest rates on these two loans are very different. In fact, interest rate charges vary a surprising amount from one lender to another, so it pays to shop around for the lowest APR. Furthermore, institutions usually charge a much higher interest rate for individuals with poor credit history. Thus, it is worth it to maintain a good credit history by paying all bills on time.
Define installment loan. A loan is amortized if both principal and interest are paid off by a sequence of equal periodic payments. This type of loan is called an installment loan. People use installment loans for cars, boats, home improvements, and even for consolidating several loans into one affordable loan. Firms use installment loans to purchase equipment, computers, vehicles, mining equipment, etc. The graphic shows the total interest that must be paid when financing a new Ford Escape over 3, 4, and 5 years. Notice that financing the SUV over 5 years results in interest costs of $2600, thereby increasing the total cost of the $25,000 loan to $27,600 or by 10.4%.

Quick TIP
The interest rates on installments loans can be very high.
Notice that the total interest paid is much higher the longer the term of the loan. It may be difficult to make the higher payments of a short-term loan, but it results in less total interest!
The federal Truth in Lending Act (Regulation Z) of 1969 requires lenders to disclose their finance charge (the charge for credit) and annual percentage rate (APR) on installment loans. The federal government does not regulate rates. Each individual state sets the maximum allowable rates and charges.
The interest rate that is stated (in the newspaper, a marketing brochure, or a problem in a textbook) is also called the nominal rate. The nominal or stated rate can differ from the annual percentage rate or APR, which is based on the actual amount received by the borrower. The APR is the true effective annual interest rate for a loan. Information on two loans of $1000 each is shown below. An advertisement indicates a rate of 10, for each loan, and the actual interest is $100 for each. However, the terms differ as do the APRs.

The interest rates on these two loans are very different. In fact, interest rate charges vary a surprising amount from one lender to another, so it pays to shop around for the lowest APR. Furthermore, institutions usually charge a much higher interest rate for individuals with poor credit history. Thus, it is worth it to maintain a good credit history by paying all bills on time.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
7
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on each note. Use the United States Rule. (See Examples 1 and 2.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the following application problem using the United States Rule.
PARTIAL PAYMENT Johnson Solar Technologies borrowed $92,000 on May 7, signing a note due in 90 days at 11.25% interest. On June 24, the company made a partial payment of $24,350. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________

PARTIAL PAYMENT Johnson Solar Technologies borrowed $92,000 on May 7, signing a note due in 90 days at 11.25% interest. On June 24, the company made a partial payment of $24,350. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
9
Find the payment necessary to amortize the following loans using the amortization table. Round to the nearest cent if needed. (See Example.)
Amortizing a Loan
Sven Yarborough earned a degree at a community college and is now a mechanic at a Ford dealership. He was so impressed with the quality of Fords that he purchased an SUV at a cost of $29,400, including tax, title, and license, after the rebate. He made a down payment of $3500 and was able to finance the balance at a rate of 6% per year for 4 years. Find (a) the monthly payment, (b) the portion of the first payment that is interest, (c) the balance due after one payment, (d) the interest owed for the second month, and (e) the balance after the second payment.

SOLUTION
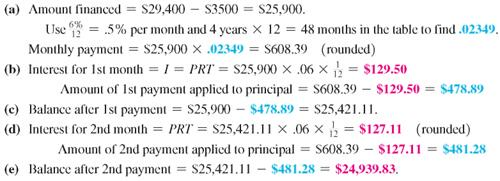

Amortizing a Loan
Sven Yarborough earned a degree at a community college and is now a mechanic at a Ford dealership. He was so impressed with the quality of Fords that he purchased an SUV at a cost of $29,400, including tax, title, and license, after the rebate. He made a down payment of $3500 and was able to finance the balance at a rate of 6% per year for 4 years. Find (a) the monthly payment, (b) the portion of the first payment that is interest, (c) the balance due after one payment, (d) the interest owed for the second month, and (e) the balance after the second payment.

SOLUTION
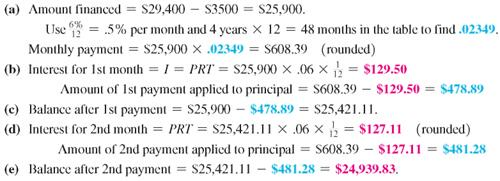


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the following application problems. Use the loan payoff table. (See Objective.)
Set up an amortization schedule.
SMART PHONE Ben Watson needs $50,000 to set up his own booth at a local mall. He has $15,000 and financed the balance at a high rate of 14% for 36 months since he did not have much credit history. Prepare an amortization schedule showing the first 5 payments.

Set up an amortization schedule.
SMART PHONE Ben Watson needs $50,000 to set up his own booth at a local mall. He has $15,000 and financed the balance at a high rate of 14% for 36 months since he did not have much credit history. Prepare an amortization schedule showing the first 5 payments.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the following application problems.
HOME PURCHASE The Potters want to buy a cottage costing $127,000 with annual insurance and taxes of $720 and $2300, respectively. They have saved $10,000 for a down payment, and they can get a
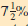 , 30-year mortgage from Citibank. They are qualified for a home loan as long as the total monthly payment does not exceed $1200. Are they qualified?
, 30-year mortgage from Citibank. They are qualified for a home loan as long as the total monthly payment does not exceed $1200. Are they qualified?
HOME PURCHASE The Potters want to buy a cottage costing $127,000 with annual insurance and taxes of $720 and $2300, respectively. They have saved $10,000 for a down payment, and they can get a
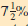 , 30-year mortgage from Citibank. They are qualified for a home loan as long as the total monthly payment does not exceed $1200. Are they qualified?
, 30-year mortgage from Citibank. They are qualified for a home loan as long as the total monthly payment does not exceed $1200. Are they qualified?
Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
12
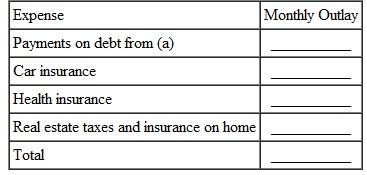
These monthly expenses do not include car insurance ($215 per month), health insurance ($290 per month), or real estate taxes and insurance on their home ($3350 per year), among other expenses. Find their total monthly outlay for all of these expenses.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
13
Round money amounts to the nearest cent and rates to the nearest tenth of a percent.
Find the required payment into a sinking fund.

Find the required payment into a sinking fund.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the following application problem using 360-day years where applicable.
Mayberry Pets borrows to purchase a van to transport animals and supplies. They agree to make quarterly payments on the $22,400 debt for 3 years at a rate of 8% compounded quarterly. Find (a) the quarterly payment __________ and (b) the total amount of interest paid. __________
Mayberry Pets borrows to purchase a van to transport animals and supplies. They agree to make quarterly payments on the $22,400 debt for 3 years at a rate of 8% compounded quarterly. Find (a) the quarterly payment __________ and (b) the total amount of interest paid. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
15
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example 2.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
16
Find the finance charge (FC) and the total installment cost (TIC) for the following. (See Example.)
Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.

Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
17
Make a list of all of the items that you have bought on an installment loan. Make another list of things you plan to buy in the next 2 years on an installment loan. (See Objective.)
Define installment loan. A loan is amortized if both principal and interest are paid off by a sequence of equal periodic payments. This type of loan is called an installment loan. People use installment loans for cars, boats, home improvements, and even for consolidating several loans into one affordable loan. Firms use installment loans to purchase equipment, computers, vehicles, mining equipment, etc. The graphic shows the total interest that must be paid when financing a new Ford Escape over 3, 4, and 5 years. Notice that financing the SUV over 5 years results in interest costs of $2600, thereby increasing the total cost of the $25,000 loan to $27,600 or by 10.4%.

Quick TIP
The interest rates on installments loans can be very high.
Notice that the total interest paid is much higher the longer the term of the loan. It may be difficult to make the higher payments of a short-term loan, but it results in less total interest!
The federal Truth in Lending Act (Regulation Z) of 1969 requires lenders to disclose their finance charge (the charge for credit) and annual percentage rate (APR) on installment loans. The federal government does not regulate rates. Each individual state sets the maximum allowable rates and charges.
The interest rate that is stated (in the newspaper, a marketing brochure, or a problem in a textbook) is also called the nominal rate. The nominal or stated rate can differ from the annual percentage rate or APR, which is based on the actual amount received by the borrower. The APR is the true effective annual interest rate for a loan. Information on two loans of $1000 each is shown below. An advertisement indicates a rate of 10, for each loan, and the actual interest is $100 for each. However, the terms differ as do the APRs.
The interest rates on these two loans are very different. In fact, interest rate charges vary a surprising amount from one lender to another, so it pays to shop around for the lowest APR. Furthermore, institutions usually charge a much higher interest rate for individuals with poor credit history. Thus, it is worth it to maintain a good credit history by paying all bills on time.
Define installment loan. A loan is amortized if both principal and interest are paid off by a sequence of equal periodic payments. This type of loan is called an installment loan. People use installment loans for cars, boats, home improvements, and even for consolidating several loans into one affordable loan. Firms use installment loans to purchase equipment, computers, vehicles, mining equipment, etc. The graphic shows the total interest that must be paid when financing a new Ford Escape over 3, 4, and 5 years. Notice that financing the SUV over 5 years results in interest costs of $2600, thereby increasing the total cost of the $25,000 loan to $27,600 or by 10.4%.

Quick TIP
The interest rates on installments loans can be very high.
Notice that the total interest paid is much higher the longer the term of the loan. It may be difficult to make the higher payments of a short-term loan, but it results in less total interest!
The federal Truth in Lending Act (Regulation Z) of 1969 requires lenders to disclose their finance charge (the charge for credit) and annual percentage rate (APR) on installment loans. The federal government does not regulate rates. Each individual state sets the maximum allowable rates and charges.
The interest rate that is stated (in the newspaper, a marketing brochure, or a problem in a textbook) is also called the nominal rate. The nominal or stated rate can differ from the annual percentage rate or APR, which is based on the actual amount received by the borrower. The APR is the true effective annual interest rate for a loan. Information on two loans of $1000 each is shown below. An advertisement indicates a rate of 10, for each loan, and the actual interest is $100 for each. However, the terms differ as do the APRs.

The interest rates on these two loans are very different. In fact, interest rate charges vary a surprising amount from one lender to another, so it pays to shop around for the lowest APR. Furthermore, institutions usually charge a much higher interest rate for individuals with poor credit history. Thus, it is worth it to maintain a good credit history by paying all bills on time.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
18
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on each note. Use the United States Rule. (See Examples 1 and 2.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
19
Solve the following application problem using the United States Rule.
REMODELING The Second Avenue Butcher Shop financed a remodeling program by giving the builder a note for $32,500. The note was made on September 14 and is due in 120 days. Interest on the note is 9.75%. On December 9, the firm makes a partial payment of $9000. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________

REMODELING The Second Avenue Butcher Shop financed a remodeling program by giving the builder a note for $32,500. The note was made on September 14 and is due in 120 days. Interest on the note is 9.75%. On December 9, the firm makes a partial payment of $9000. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
20
Find the payment necessary to amortize the following loans using the amortization table. Round to the nearest cent if needed. (See Example.)
Amortizing a Loan
Sven Yarborough earned a degree at a community college and is now a mechanic at a Ford dealership. He was so impressed with the quality of Fords that he purchased an SUV at a cost of $29,400, including tax, title, and license, after the rebate. He made a down payment of $3500 and was able to finance the balance at a rate of 6% per year for 4 years. Find (a) the monthly payment, (b) the portion of the first payment that is interest, (c) the balance due after one payment, (d) the interest owed for the second month, and (e) the balance after the second payment.

SOLUTION
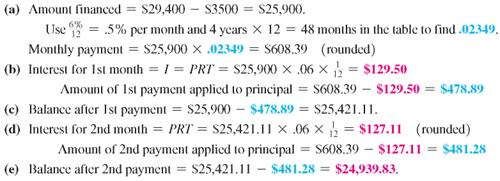

Amortizing a Loan
Sven Yarborough earned a degree at a community college and is now a mechanic at a Ford dealership. He was so impressed with the quality of Fords that he purchased an SUV at a cost of $29,400, including tax, title, and license, after the rebate. He made a down payment of $3500 and was able to finance the balance at a rate of 6% per year for 4 years. Find (a) the monthly payment, (b) the portion of the first payment that is interest, (c) the balance due after one payment, (d) the interest owed for the second month, and (e) the balance after the second payment.

SOLUTION
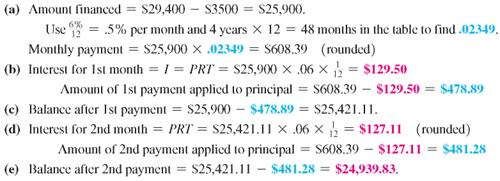


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
21
Solve the following application problems. Use the loan payoff table. (See Objective.)
Set up an amortization schedule.
SCUBA EQUIPMENT Jessica Chien needed $280,000 for inventory for a scuba diving shop that she was opening. She had $40,000, and the bank loaned her the balance at 11% for 30 months. Prepare an amortization schedule showing the first 5 payments.


Set up an amortization schedule.
SCUBA EQUIPMENT Jessica Chien needed $280,000 for inventory for a scuba diving shop that she was opening. She had $40,000, and the bank loaned her the balance at 11% for 30 months. Prepare an amortization schedule showing the first 5 payments.



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the following application problems.
CONDOMINIUM PURCHASE The Polinki family wants to buy a condominium that costs $225,000 with annual insurance and taxes of $850 and $3200, respectively. They plan to pay $20,000 down and amortize the balance at 8% per year for 25 years. They are qualified for a loan as long as the payments do not exceed $1800. Are they qualified for the loan?
CONDOMINIUM PURCHASE The Polinki family wants to buy a condominium that costs $225,000 with annual insurance and taxes of $850 and $3200, respectively. They plan to pay $20,000 down and amortize the balance at 8% per year for 25 years. They are qualified for a loan as long as the payments do not exceed $1800. Are they qualified for the loan?

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
23
CITIGROUP INC.-HOME FINANCING
www.citigroup.com Facts:
• 1812: Founded in New York City
• 1914: Opened first international branch, in Argentina
• 1998: Merged with Travelers Insurance Group
• 2008: Lost $27.7 billion Took funds from government during financial crisis
• 2010: Revenue estimated to fall 40% compared to 2007
Citigroup Inc. (Citi) provides various banking, lending, insurance, and investment services to individual and corporate customers worldwide. It operates more than 7200 branches and 7000 ATMs. Citi had more than $150 billion in credit-card loans outstanding in 2010 in addition to huge volumes of home loans and business loans.
The financial crisis of 2008-10 created very serious problems for Citigroup. To illustrate the nature of some of the problems, we use the example of one family: Tom and Marie Duston purchased their first home in 2008 when home loans were still very easy to get. They bought a beautiful new 4-bedroom, -bath home with a down payment of only $8500.
At the time of the purchase in 2008, the Dustons were told that the interest rate on their ARM loan would reset in 2011, so they knew the payments might increase. However, they were not worried since they assumed that their incomes and also the value of the house would be higher by then. But home prices fell across much of the country in 2008-11, as did the value of their home. By 2011, an appraiser estimated that it was worth only 75% of the original loan balance of $306,500, which they still owed. They were underwater on their home! Find out what the house was worth in 2011 and the amount by which they were underwater.
www.citigroup.com Facts:
• 1812: Founded in New York City
• 1914: Opened first international branch, in Argentina
• 1998: Merged with Travelers Insurance Group
• 2008: Lost $27.7 billion Took funds from government during financial crisis
• 2010: Revenue estimated to fall 40% compared to 2007
Citigroup Inc. (Citi) provides various banking, lending, insurance, and investment services to individual and corporate customers worldwide. It operates more than 7200 branches and 7000 ATMs. Citi had more than $150 billion in credit-card loans outstanding in 2010 in addition to huge volumes of home loans and business loans.
The financial crisis of 2008-10 created very serious problems for Citigroup. To illustrate the nature of some of the problems, we use the example of one family: Tom and Marie Duston purchased their first home in 2008 when home loans were still very easy to get. They bought a beautiful new 4-bedroom, -bath home with a down payment of only $8500.
At the time of the purchase in 2008, the Dustons were told that the interest rate on their ARM loan would reset in 2011, so they knew the payments might increase. However, they were not worried since they assumed that their incomes and also the value of the house would be higher by then. But home prices fell across much of the country in 2008-11, as did the value of their home. By 2011, an appraiser estimated that it was worth only 75% of the original loan balance of $306,500, which they still owed. They were underwater on their home! Find out what the house was worth in 2011 and the amount by which they were underwater.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
24
Solve the following application problems.
Mock Construction bought a truck and financed $7400 with 48 monthly payments of $228.14 each. Suppose the firm pays the loan off with 12 payments left. Use the Rule of 78 to find (a) the amount of unearned interest and (b) the amount necessary to pay off the loan. __________
Mock Construction bought a truck and financed $7400 with 48 monthly payments of $228.14 each. Suppose the firm pays the loan off with 12 payments left. Use the Rule of 78 to find (a) the amount of unearned interest and (b) the amount necessary to pay off the loan. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the following application problems using 360-day years where applicable.
The Hodges purchase an older 4-bedroom home for $195,000 with 5 down. They finance the balance at
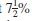 per year for 30 years. If insurance is $720 per year and taxes are $4140 per year, find the monthly payment.
per year for 30 years. If insurance is $720 per year and taxes are $4140 per year, find the monthly payment.
The Hodges purchase an older 4-bedroom home for $195,000 with 5 down. They finance the balance at
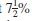 per year for 30 years. If insurance is $720 per year and taxes are $4140 per year, find the monthly payment.
per year for 30 years. If insurance is $720 per year and taxes are $4140 per year, find the monthly payment.
Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
26
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example 2.)
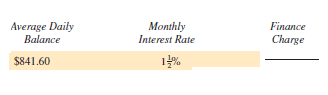
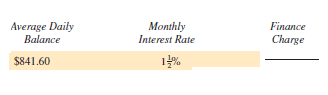

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
27
Find the finance charge (FC) and the total installment cost (TIC) for the following. (See Example.)
Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.

Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the following application problems. Use the formula on page 505 to estimate the APR, and round rates to the nearest tenth of a percent.
METAL LATHE Benson Fabrication purchased a new precision metal lathe for $74,800. The company made a down payment of 20% and financed the balance using 36 monthly payments of $1916.85. Find (a) the amount financed, (b) the total installment cost, and (c) the finance charge. (d) Then estimate the APR.
METAL LATHE Benson Fabrication purchased a new precision metal lathe for $74,800. The company made a down payment of 20% and financed the balance using 36 monthly payments of $1916.85. Find (a) the amount financed, (b) the total installment cost, and (c) the finance charge. (d) Then estimate the APR.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
29
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on the note. Use the United States Rule. (See Examples.)
Finding the Amount Due
On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

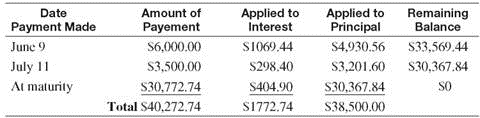
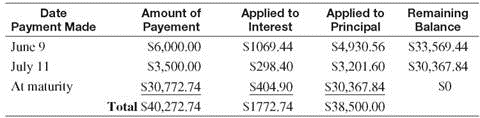
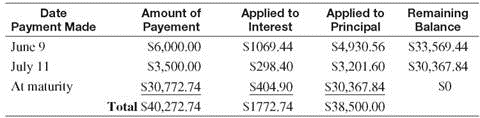
On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.


Finding the Amount Due

On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.




Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the following application problem using the United States Rule.
INVENTORY The Washington News orders large quantities of paper every 4 months to save on freight charges. For its last order, the firm signed a note on February 18, maturing on May 15. The face value of the note was $104,500, with interest of 11%. The firm made a partial payment of $38,000 on March 20 and a second partial payment of $27,200 on April 16. Find (a) the amount due on the maturity date of the note __________ and (b) the amount of interest paid on the note. __________
INVENTORY The Washington News orders large quantities of paper every 4 months to save on freight charges. For its last order, the firm signed a note on February 18, maturing on May 15. The face value of the note was $104,500, with interest of 11%. The firm made a partial payment of $38,000 on March 20 and a second partial payment of $27,200 on April 16. Find (a) the amount due on the maturity date of the note __________ and (b) the amount of interest paid on the note. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
31
Use the loan payoff table to find the monthly payment (MP) and finance charge (FC) for each of the following loans. (See Example 3.)
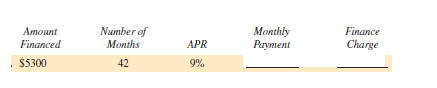
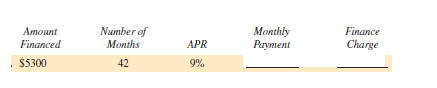

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
32
Use the real estate amortization table to find the monthly payment for the following loans. (See Example 1.)
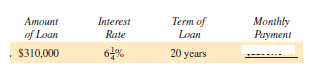
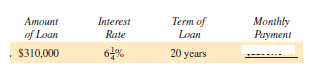

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the following application problems.
HOME LOAN June and Bill Able borrow $122,500 on their home at
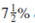 for 15 years. Prepare a repayment schedule for the first two payments. (See Example.)
for 15 years. Prepare a repayment schedule for the first two payments. (See Example.)
Preparing a Repayment Schedule
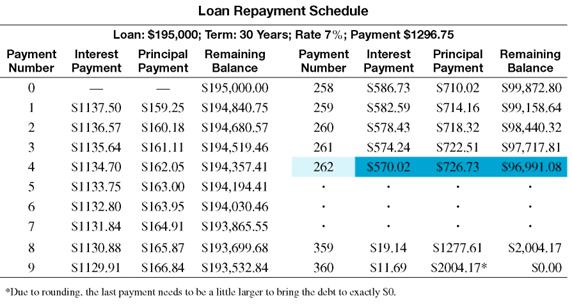
The Zinks purchase a house by borrowing $195,000 at 7% for 30 years. Prepare a loan repayment schedule for this loan.

SOLUTION
First find the monthly payment, then use simple interest calculations for the first two months. Be sure to round to the nearest cent at each step.

Every time a payment is made, interest is first subtracted from the payment. As a result, only a small portion of the first payment is applied to reduce the principal.
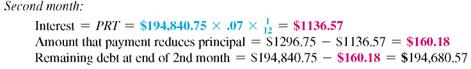
These and other results are shown in the table. Notice that at first the amount applied to interest is large and the amount applied to reduce principal is small. But every month, the debt goes down, resulting in lower interest the following month, and more of each payment is applied to reduce the principal. It requires 262 months (nearly 22 years) to pay off half of the debt and only 98 months (just over 8 years) to pay off the other half of the loan.

HOME LOAN June and Bill Able borrow $122,500 on their home at
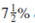 for 15 years. Prepare a repayment schedule for the first two payments. (See Example.)
for 15 years. Prepare a repayment schedule for the first two payments. (See Example.)Preparing a Repayment Schedule
The Zinks purchase a house by borrowing $195,000 at 7% for 30 years. Prepare a loan repayment schedule for this loan.

SOLUTION
First find the monthly payment, then use simple interest calculations for the first two months. Be sure to round to the nearest cent at each step.

Every time a payment is made, interest is first subtracted from the payment. As a result, only a small portion of the first payment is applied to reduce the principal.
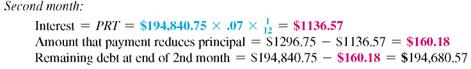
These and other results are shown in the table. Notice that at first the amount applied to interest is large and the amount applied to reduce principal is small. But every month, the debt goes down, resulting in lower interest the following month, and more of each payment is applied to reduce the principal. It requires 262 months (nearly 22 years) to pay off half of the debt and only 98 months (just over 8 years) to pay off the other half of the loan.



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
34
To help you review, the numbers in brackets show the section in which the topic was discussed.
Solve for following problems.
The balance on John Baker's MasterCard on November 1 is $680.45. In November, he charges an additional $337.32, has returns of $45.42, and makes a payment of $50. If the finance charges are calculated at 1.5% per month on the unpaid balance, find his balance on December 1. __________
Solve for following problems.
The balance on John Baker's MasterCard on November 1 is $680.45. In November, he charges an additional $337.32, has returns of $45.42, and makes a payment of $50. If the finance charges are calculated at 1.5% per month on the unpaid balance, find his balance on December 1. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
35
Round money amounts to the nearest cent and rates to the nearest tenth of a percent.
Find the required payment into a sinking fund.

Find the required payment into a sinking fund.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the following application problem using 360-day years where applicable.
On January 10, Bob Jones signed a 200-day note for $24,000 to finance some work on a roof. The note was at 9% per year simple interest. Due to an unexpected income tax refund, he was able to repay $10,000 on April 15. Use the United States Rule and (a) find the balance owed on the principal after the partial payment. __________ (b) Then find the amount due at maturity of the loan. __________
On January 10, Bob Jones signed a 200-day note for $24,000 to finance some work on a roof. The note was at 9% per year simple interest. Due to an unexpected income tax refund, he was able to repay $10,000 on April 15. Use the United States Rule and (a) find the balance owed on the principal after the partial payment. __________ (b) Then find the amount due at maturity of the loan. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
37
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example.)
Finding the Average Daily Balance
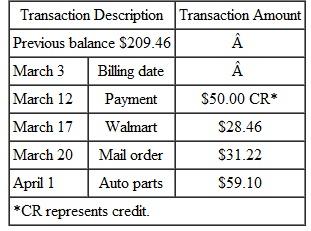
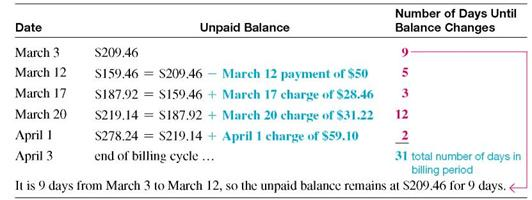
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION
(a)
Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).
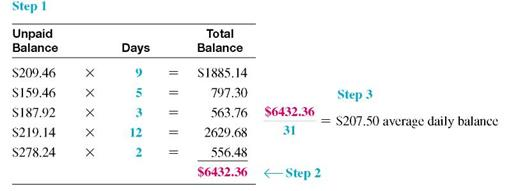
Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
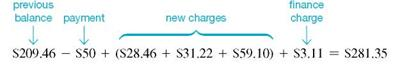

Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION (a)

Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).

Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
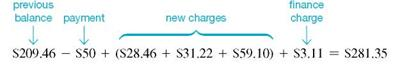


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
38
Find the finance charge (FC) and the total installment cost (TIC) for the following. (See Example.)
Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.

Finding the Total Installment Cost
Frank Kimlicko recently received his master's degree and began work at a large community college as a music professor specializing in classical guitar. He purchased an exquisite-sounding classical guitar costing $3800 with $500 down and 36 monthly payments of $109.61 each. Find (a) the total installment cost, (b) the finance charge, and (c) the amount financed.
Quick TIP
To find the total installment cost, add the down payment to the sum of all monthly payments.
SOLUTION
(a) The total installment cost is the down payment plus the total of all monthly payments.
Total installment cost = $500 + 1$109.61 × 362 = $4445.96
(b) The finance charge is the total installment cost less the cash price.
Finance charge = $4445.96 ? $ 3800 = $645.96
(c) The amount financed is $3800 ? $500 = $3300.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the following application problem. Use formula to estimate the APR, and round rates to the nearest tenth of a percent.
PLAYSET Tom and Jane Franklin bought a backyard playset with a trampoline for their grandchildren for $9400. They paid 10% down and financed the balance with 24 monthly payments of $398.24. Find (a) the amount financed,___________ (b) the total installment cost,___________ and (c) the finance charge. ___________ (d) Then estimate the APR.___________
PLAYSET Tom and Jane Franklin bought a backyard playset with a trampoline for their grandchildren for $9400. They paid 10% down and financed the balance with 24 monthly payments of $398.24. Find (a) the amount financed,___________ (b) the total installment cost,___________ and (c) the finance charge. ___________ (d) Then estimate the APR.___________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
40
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on the note. Use the United States Rule. (See Examples.)
Finding the Amount Due
On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.


Finding the Amount Due

On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.




Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the following application problem using the United States Rule.
SURVEILLANCE CAMERAS To help detect trespassers at night, a small security firm purchased some high-technology cameras using a note from Citibank for $32,000. The note was signed on July 26 and was due on November 20. The interest rate is 13%. The firm made a partial payment of $6000 on August 31 and a second partial payment of $11,700 on October 4. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________
SURVEILLANCE CAMERAS To help detect trespassers at night, a small security firm purchased some high-technology cameras using a note from Citibank for $32,000. The note was signed on July 26 and was due on November 20. The interest rate is 13%. The firm made a partial payment of $6000 on August 31 and a second partial payment of $11,700 on October 4. Find (a) the amount due on the maturity date of the note __________ and (b) the interest paid on the note. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
42
Use the loan payoff table to find the monthly payment (MP) and finance charge (FC) for each of the following loans. (See Example 3.)
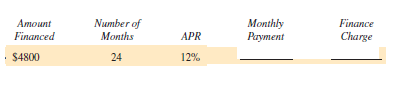
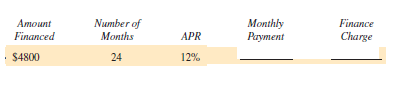

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
43
Use the real estate amortization table to find the monthly payment for the following loans. (See Example 1.)
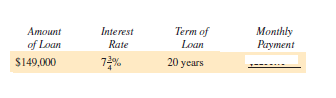


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the following application problems.
ELDERLY HOUSING Tom Ajax purchases a tiny home for his elderly mother. After a large down payment, he finances $88,600 at
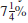 for 10 years. Prepare a repayment schedule for the first two payments. (See Example 2.)
for 10 years. Prepare a repayment schedule for the first two payments. (See Example 2.)

ELDERLY HOUSING Tom Ajax purchases a tiny home for his elderly mother. After a large down payment, he finances $88,600 at
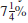 for 10 years. Prepare a repayment schedule for the first two payments. (See Example 2.)
for 10 years. Prepare a repayment schedule for the first two payments. (See Example 2.)

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
45
Round money amounts to the nearest cent and rates to the nearest tenth of a percent.
Find the amount of each annuity due and the interest earned.

Find the amount of each annuity due and the interest earned.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
46
Find the amount of each payment necessary to amortize the following loans.
Jenson SawLogs borrows $34,500 to buy a new electric generator. The company agrees to make quarterly payments for 2 years at 10% per year. Find the amount of the quarterly payment. ___________
Jenson SawLogs borrows $34,500 to buy a new electric generator. The company agrees to make quarterly payments for 2 years at 10% per year. Find the amount of the quarterly payment. ___________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the following application problem using 360-day years where applicable.
Karoline Jacobs borrowed $2200 for new kitchen appliances. She agreed to pay the loan back with 8 payments of $290.69 each. After 3 payments, she decides to go ahead and pay off the loan in full. Use the Rule of 78 to find (a) the amount of unearned interest __________ and (b) the amount needed to repay the loan in full. __________ [12.3]
Karoline Jacobs borrowed $2200 for new kitchen appliances. She agreed to pay the loan back with 8 payments of $290.69 each. After 3 payments, she decides to go ahead and pay off the loan in full. Use the Rule of 78 to find (a) the amount of unearned interest __________ and (b) the amount needed to repay the loan in full. __________ [12.3]

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
48
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example.)
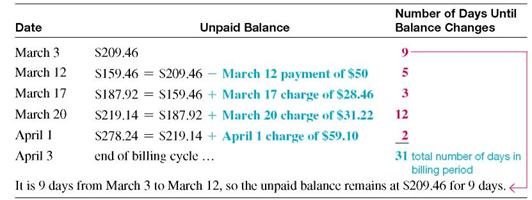
Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
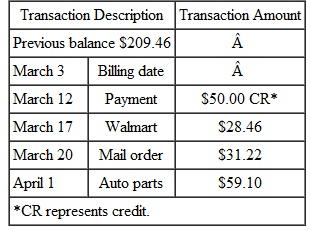 SOLUTION
SOLUTION
(a)
Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).
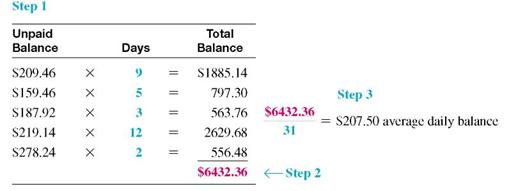
Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
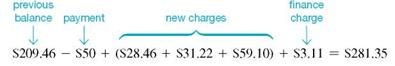

Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION (a)

Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).

Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
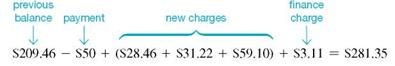


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
49
Find the approximate annual percentage rate using the approximate annual percentage rate formula. Round to the nearest tenth of a percent. (See Example 2.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the following application problem. Use formula to estimate the APR, and round rates to the nearest tenth of a percent.
ELECTRIC GUITAR Yanni Benjamin purchased a good-quality electric guitar with amplifier and financed $3600 over 12 months. The finance charge was $260. (a) Estimate the APR,___________ then (b) find the exact APR using the table.___________

ELECTRIC GUITAR Yanni Benjamin purchased a good-quality electric guitar with amplifier and financed $3600 over 12 months. The finance charge was $260. (a) Estimate the APR,___________ then (b) find the exact APR using the table.___________


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
51
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on the note. Use the United States Rule. (See Examples.)
Finding the Amount Due
On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.


Finding the Amount Due

On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.




Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the following application problems using the Rule of 78. (See Example 3.)
ENGAGEMENT RING Tom Stowe purchased a diamond engagement ring for $1150. He paid $100 down and agreed to 12 monthly payments of $95 each. After making 7 payments, he paid the loan in full. Find (a) the unearned interest and (b) the amount necessary to pay the loan in full.
ENGAGEMENT RING Tom Stowe purchased a diamond engagement ring for $1150. He paid $100 down and agreed to 12 monthly payments of $95 each. After making 7 payments, he paid the loan in full. Find (a) the unearned interest and (b) the amount necessary to pay the loan in full.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
53
Use the loan payoff table to find the monthly payment (MP) and finance charge (FC) for each of the following loans. (See Example.)
Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
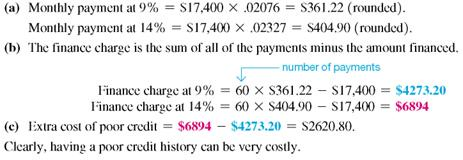

Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
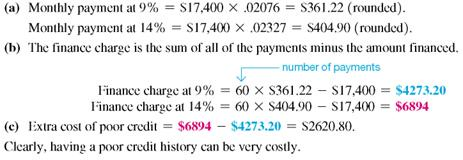


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
54
Use the real estate amortization table to find the monthly payment for the following loans. (See Example 1.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
55
Roberto and Julie Hernandez are struggling to make their monthly payments. They accumulated too much debt, which was easy to do with two young kids at home. Julie works 30 hours a week and takes care of the two kids. Their credit history had been poor, but Roberto took on a second job during the evenings and they have been making payments regularly for 8 months.
After discussing things with Jackie Waterton at Citibank, the Hernandez's have learned that they can (1) refinance the remaining $14,900 amount on the Honda Accord at 12 over 4 years, (2) refinance the remaining $8600 loan amount on the Ford truck at 12 over 3 years, (3) refinance the remaining $94,800 loan amount on their home at 8 over 30 years, and (4) reduce their car insurance payments by $28 per month. Complete the following table.

After discussing things with Jackie Waterton at Citibank, the Hernandez's have learned that they can (1) refinance the remaining $14,900 amount on the Honda Accord at 12 over 4 years, (2) refinance the remaining $8600 loan amount on the Ford truck at 12 over 3 years, (3) refinance the remaining $94,800 loan amount on their home at 8 over 30 years, and (4) reduce their car insurance payments by $28 per month. Complete the following table.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the following application problems using 360-day years where applicable.
At 58, Thomas Jones knows that he needs to save more. He decides to invest $300 per quarter in an account paying 10 compounded quarterly. Find the accumulated amount (a) at age 65 and (b) at age 70.
At 58, Thomas Jones knows that he needs to save more. He decides to invest $300 per quarter in an account paying 10 compounded quarterly. Find the accumulated amount (a) at age 65 and (b) at age 70.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the following application problems using 360-day years where applicable.
Waterford Landscaping lost a lawsuit and must pay the injured party $3500 at the end of each quarter for 1 year. If funds earn 8 compounded quarterly, find the amount that needs to be set aside today to fulfill this obligation.
Waterford Landscaping lost a lawsuit and must pay the injured party $3500 at the end of each quarter for 1 year. If funds earn 8 compounded quarterly, find the amount that needs to be set aside today to fulfill this obligation.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
58
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example.)
Finding the Average Daily Balance
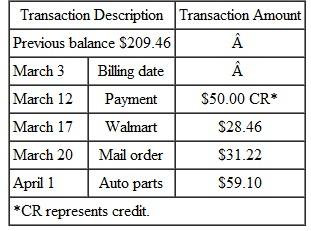
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION
(a)
Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
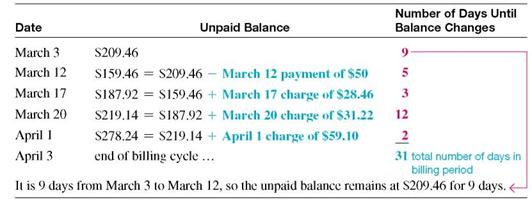
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).
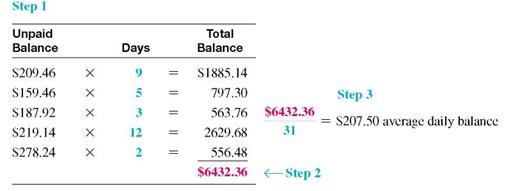
Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
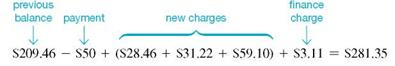

Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION (a)

Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).

Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
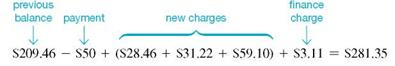


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
59
Find the approximate annual percentage rate using the approximate annual percentage rate formula. Round to the nearest tenth of a percent. (See Example.)
Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
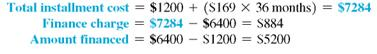
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.

Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
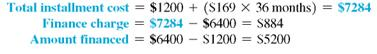
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the following application problem. Use formula to estimate the APR, and round rates to the nearest tenth of a percent.
CANNING MACHINE Aluminum Cans Inc. purchased a new machine to press aluminum into cans and financed $385,000 over 30 months. The finance charge was $54,411. (a) Estimate the APR, __________ then (b) find the exact APR using the table. __________
CANNING MACHINE Aluminum Cans Inc. purchased a new machine to press aluminum into cans and financed $385,000 over 30 months. The finance charge was $54,411. (a) Estimate the APR, __________ then (b) find the exact APR using the table. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
61
Find the balance due on the maturity date of the following notes. Find the total amount of interest paid on the note. Use the United States Rule. (See Examples.)
Finding the Amount Due
On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.

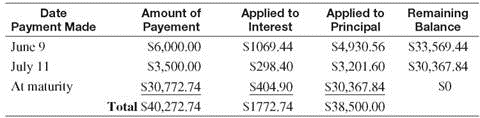

Finding the Amount Due

On August 14, Dr. Jane Ficker signed a 180-day note for $28,500 for a used x-ray machine for her dental office. The note has an interest rate of 10% compounded annually. On October 25, a payment of $8500 is made. (a) Find the balance owed on the principal after the payment. (b) If no additional payments are made, find the amount due at maturity of the loan.
SOLUTION

Finding the Interest Paid and Amount Due

On March 1, Boston Dairy signs a promissory note for $38,500 to replace some milking equipment for their Holsteins. The note is for 180 days at a rate of 10%. The dairy makes the following partial payments: $6000 on June 9 and $3500 on July 11. Find the interest paid on the note and the amount due on the due date of the note.
SOLUTION
The first partial payment is on June 9 or, using the number of days in each month, after
(30 + 30 + 31 + 9) = 100 days.

Debt on July 11 after 2nd partial payment = $33,569.44 ? $3201.60 = $ 30,367.84
The first partial payment is made after 100 days, and the second partial payment is made after an additional 32 days. Thus, the due date of the note is 180 ? 100 ? 32 = 48 days after the second partial payment.




Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the following application problems using the Rule of 78. (See Example.)
Finding Unearned Interest and Balance Due
Aaron Ortego borrowed $6000, which he is paying back in 24 monthly payments of $295 each. With 9 payments remaining, he decides to repay the loan in full. Find (a) the amount of unearned interest and (b) the amount necessary to repay the loan in full. Use the Rule of 78.
SOLUTION
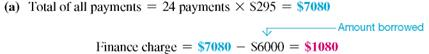
Find the amount of unearned interest as follows. The finance charge is $1080, the scheduled number of payments is 24, and the loan is paid off with 9 payments left. Solve as follows.
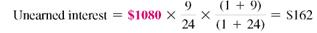
(b) When Ortego decides to pay off the loan, he has 9 payments of $295 left.
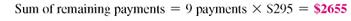
Ortego saves the unearned interest of $162 by paying off the loan early. Therefore, the amount needed to pay the loan in full is the sum of the remaining payments minus the unearned interest.
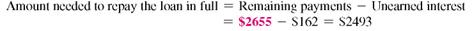
GARBAGE TRUCK Haul-it-Away, Inc., purchased a dump truck for $62,000. The owners made a down payment of $22,000 and financed the remainder with 36 payments of $1328.57 each. They paid off the note with 12 payments remaining. Find (a) the amount of unearned interest __________ and (b) the amount necessary to pay the loan in full. __________
Finding Unearned Interest and Balance Due
Aaron Ortego borrowed $6000, which he is paying back in 24 monthly payments of $295 each. With 9 payments remaining, he decides to repay the loan in full. Find (a) the amount of unearned interest and (b) the amount necessary to repay the loan in full. Use the Rule of 78.
SOLUTION
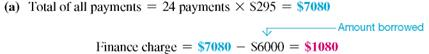
Find the amount of unearned interest as follows. The finance charge is $1080, the scheduled number of payments is 24, and the loan is paid off with 9 payments left. Solve as follows.
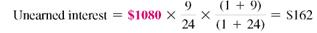
(b) When Ortego decides to pay off the loan, he has 9 payments of $295 left.
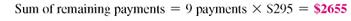
Ortego saves the unearned interest of $162 by paying off the loan early. Therefore, the amount needed to pay the loan in full is the sum of the remaining payments minus the unearned interest.
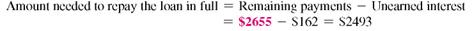
GARBAGE TRUCK Haul-it-Away, Inc., purchased a dump truck for $62,000. The owners made a down payment of $22,000 and financed the remainder with 36 payments of $1328.57 each. They paid off the note with 12 payments remaining. Find (a) the amount of unearned interest __________ and (b) the amount necessary to pay the loan in full. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
63
Use the loan payoff table to find the monthly payment (MP) and finance charge (FC) for each of the following loans. (See Example.)
Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
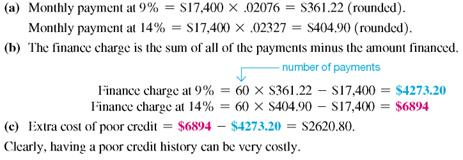

Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
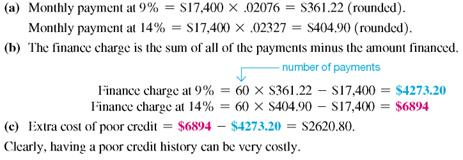


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
64
Use the real estate amortization table to find the monthly payment for the following loans. (See Example.)
Understanding the Effects of Rate and Term
After making a down payment, the Stringers need to borrow $140,000 to purchase a condominium. They want to know the effect of the interest rate and term of the loan on cost. (a) Find the monthly payment for both 15 and 30 years at 4% and 6%. Then find (b) the total cost of the home with each loan and (c) the finance charge for each loan.
Quick TIP
Be sure to divide the loan amount by $1000 before calculating the monthly payment.
SOLUTION
(a) The amount to be financed in thousands = $140,000 ÷ $1000 = 140. Multiply this value by the appropriate factor from the real estate amortization table.
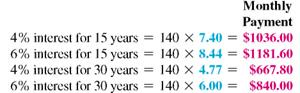
Monthly payments range from $667.80 to $1181.60, depending on the interest rate and length of the loan. The lowest payment of $667.80 may look good at first, but read part (b) below.
(b) The total cost of the home is the sum of all payments over the respective months and years.
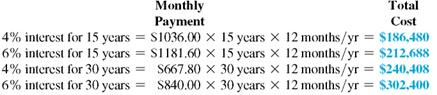
(c) The finance charge, or interest cost, of each of the loans is the total cost found in part (b) minus the amount financed of $140,000.
Quick TIP
You can reduce your long-term cost of a mortgage by paying more than the required payment every month. Even an extra $60 per month can make a big difference over the long run.
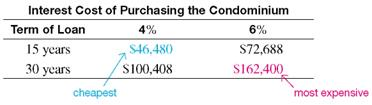
First, notice that interest adds quite a bit to the cost of the $140,000 loan. The longer term of 30 years results in a significantly lower house payment, but it also results in a much higher eventual cost. So, the longer term loan of 30 years is not necessarily the best choice. Clearly, higher interest rates and longer terms ADD HUGE amounts to the interest that must be paid to purchase a property.

Understanding the Effects of Rate and Term
After making a down payment, the Stringers need to borrow $140,000 to purchase a condominium. They want to know the effect of the interest rate and term of the loan on cost. (a) Find the monthly payment for both 15 and 30 years at 4% and 6%. Then find (b) the total cost of the home with each loan and (c) the finance charge for each loan.
Quick TIP
Be sure to divide the loan amount by $1000 before calculating the monthly payment.
SOLUTION
(a) The amount to be financed in thousands = $140,000 ÷ $1000 = 140. Multiply this value by the appropriate factor from the real estate amortization table.
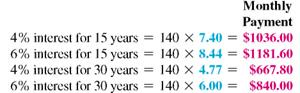
Monthly payments range from $667.80 to $1181.60, depending on the interest rate and length of the loan. The lowest payment of $667.80 may look good at first, but read part (b) below.
(b) The total cost of the home is the sum of all payments over the respective months and years.
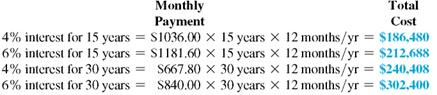
(c) The finance charge, or interest cost, of each of the loans is the total cost found in part (b) minus the amount financed of $140,000.
Quick TIP
You can reduce your long-term cost of a mortgage by paying more than the required payment every month. Even an extra $60 per month can make a big difference over the long run.

First, notice that interest adds quite a bit to the cost of the $140,000 loan. The longer term of 30 years results in a significantly lower house payment, but it also results in a much higher eventual cost. So, the longer term loan of 30 years is not necessarily the best choice. Clearly, higher interest rates and longer terms ADD HUGE amounts to the interest that must be paid to purchase a property.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
65
CITIGROUP INC.-HOME FINANCING
www.citigroup.com Facts:
• 1812: Founded in New York City
• 1914: Opened first international branch, in Argentina
• 1998: Merged with Travelers Insurance Group
• 2008: Lost $27.7 billion Took funds from government during financial crisis
• 2010: Revenue estimated to fall 40% compared to 2007
Citigroup Inc. (Citi) provides various banking, lending, insurance, and investment services to individual and corporate customers worldwide. It operates more than 7200 branches and 7000 ATMs. Citi had more than $150 billion in credit-card loans outstanding in 2010 in addition to huge volumes of home loans and business loans.
The financial crisis of 2008-10 created very serious problems for Citigroup. To illustrate the nature of some of the problems, we use the example of one family: Tom and Marie Duston purchased their first home in 2008 when home loans were still very easy to get. They bought a beautiful new 4-bedroom, -bath home with a down payment of only $8500.
The Dustons were shocked to find out that they would have to come up with $76,625 to pay off the bank loan to sell their home. They were further shocked to find out they would also need to come up with an additional $23,000 to pay various expenses, such as the real estate commission related to the sale of their home. Estimate the total amount they would have to pay to sell their home, rounded to the nearest thousand.
www.citigroup.com Facts:
• 1812: Founded in New York City
• 1914: Opened first international branch, in Argentina
• 1998: Merged with Travelers Insurance Group
• 2008: Lost $27.7 billion Took funds from government during financial crisis
• 2010: Revenue estimated to fall 40% compared to 2007
Citigroup Inc. (Citi) provides various banking, lending, insurance, and investment services to individual and corporate customers worldwide. It operates more than 7200 branches and 7000 ATMs. Citi had more than $150 billion in credit-card loans outstanding in 2010 in addition to huge volumes of home loans and business loans.
The financial crisis of 2008-10 created very serious problems for Citigroup. To illustrate the nature of some of the problems, we use the example of one family: Tom and Marie Duston purchased their first home in 2008 when home loans were still very easy to get. They bought a beautiful new 4-bedroom, -bath home with a down payment of only $8500.
The Dustons were shocked to find out that they would have to come up with $76,625 to pay off the bank loan to sell their home. They were further shocked to find out they would also need to come up with an additional $23,000 to pay various expenses, such as the real estate commission related to the sale of their home. Estimate the total amount they would have to pay to sell their home, rounded to the nearest thousand.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
66
Find the amount of each payment necessary to amortize the following loans.
Scented Candles remodeled its lobby at a cost of $36,000. It pays $6000 down and pays off the balance in payments made at the end of each quarter for 5 years. Interest is 10% compounded quarterly. Find the amount of each payment so that the loan is fully amortized. ___________
Scented Candles remodeled its lobby at a cost of $36,000. It pays $6000 down and pays off the balance in payments made at the end of each quarter for 5 years. Interest is 10% compounded quarterly. Find the amount of each payment so that the loan is fully amortized. ___________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the following application problem using 360-day years where applicable.
James Booker signs an employment contract that guarantees him $35,000 at the end of each year for 3 years when he retires in 4 years. If funds earn 8% per year, find the present value needed today to meet the eventual payment stream. __________
James Booker signs an employment contract that guarantees him $35,000 at the end of each year for 3 years when he retires in 4 years. If funds earn 8% per year, find the present value needed today to meet the eventual payment stream. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
68
Find the finance charge for the following revolving charge accounts. Assume that interest is calculated on the average daily balance of the account. (See Example.)
Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
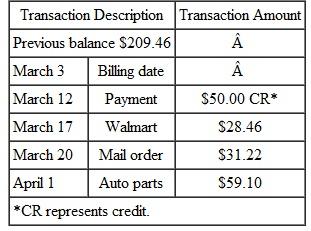 SOLUTION
SOLUTION
(a)
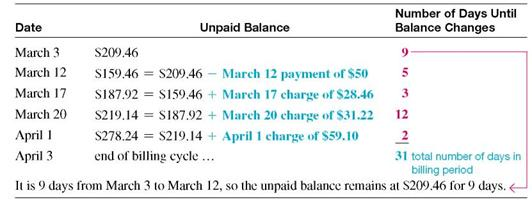
Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).
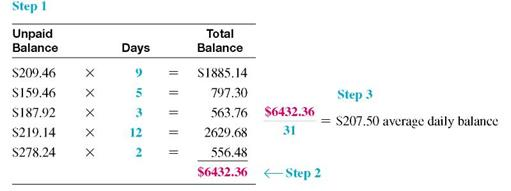
Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
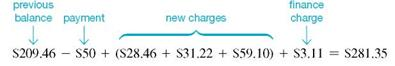

Finding the Average Daily Balance
Beth Hogan's balance on a Visa card was $209.46 on March 3. Her activity for the next 30 days is shown in the table. (a) Find the average daily balance on April 3. Given finance charges based on 1 1 2 % on the average daily balance, find (b) the finance charge for the month and (c) the balance owed on April 3.
 SOLUTION
SOLUTION (a)

Quick TIP
The billing period in Example is 31 days. Some billing periods are 30 days (or 28 or 29 days in February). Be sure to use the correct number of days for the month of the billing period.
There are 31 days in the billing period (March has 31 days). Find the average daily balance as follows:
Step 1 Multiply each unpaid balance by the number of days for that balance.
Step 2 Total these amounts.
Step 3 Divide by the number of days in that particular billing cycle (month).

Hogan will pay a finance charge based on the average daily balance of $207.50.
(b) The finance charge is.015 × $207.50 = $3.11 (rounded).(c) The amount owed on April 3 is the beginning unpaid balance less any returns or payments, plus new charges and the finance charge.
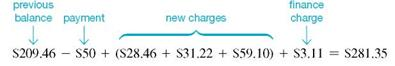


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
69
Find the approximate annual percentage rate using the approximate annual percentage rate formula. Round to the nearest tenth of a percent. (See Example.)
Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
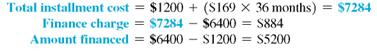
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.

Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
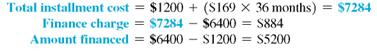
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the following application problems and use the table to find the annual percentage rate.
CHIP FABRICATION A Chinese computer chip manufacturer borrowed $84 million worth of Chinese yuan to purchase some sophisticated equipment. The note required 24 monthly payments of $3.88 million each. Find the annual percentage rate.
CHIP FABRICATION A Chinese computer chip manufacturer borrowed $84 million worth of Chinese yuan to purchase some sophisticated equipment. The note required 24 monthly payments of $3.88 million each. Find the annual percentage rate.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
71
Each of the following loans is paid in full before the date of maturity. Find the amount of unearned interest. Use the Rule of 78. (See Example 3.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the following application problems using the Rule of 78. (See Example.)
Finding Unearned Interest and Balance Due
Aaron Ortego borrowed $6000, which he is paying back in 24 monthly payments of $295 each. With 9 payments remaining, he decides to repay the loan in full. Find (a) the amount of unearned interest and (b) the amount necessary to repay the loan in full. Use the Rule of 78.
SOLUTION
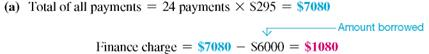
Find the amount of unearned interest as follows. The finance charge is $1080, the scheduled number of payments is 24, and the loan is paid off with 9 payments left. Solve as follows.
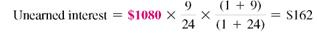
(b) When Ortego decides to pay off the loan, he has 9 payments of $295 left.
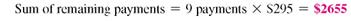
Ortego saves the unearned interest of $162 by paying off the loan early. Therefore, the amount needed to pay the loan in full is the sum of the remaining payments minus the unearned interest.
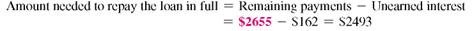
PRINTING BlackTop Printing made a $5000 down payment on a special copy machine costing $23,800. The loan agreement with Citibank called for 20 monthly payments of $1025 each. Find (a) the finance charge, __________ (b) the unearned interest, __________ and (c) the amount necessary to pay the loan in full after the 14th payment. __________
Finding Unearned Interest and Balance Due
Aaron Ortego borrowed $6000, which he is paying back in 24 monthly payments of $295 each. With 9 payments remaining, he decides to repay the loan in full. Find (a) the amount of unearned interest and (b) the amount necessary to repay the loan in full. Use the Rule of 78.
SOLUTION
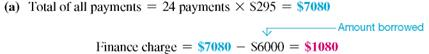
Find the amount of unearned interest as follows. The finance charge is $1080, the scheduled number of payments is 24, and the loan is paid off with 9 payments left. Solve as follows.
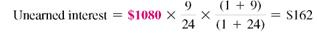
(b) When Ortego decides to pay off the loan, he has 9 payments of $295 left.
Ortego saves the unearned interest of $162 by paying off the loan early. Therefore, the amount needed to pay the loan in full is the sum of the remaining payments minus the unearned interest.
PRINTING BlackTop Printing made a $5000 down payment on a special copy machine costing $23,800. The loan agreement with Citibank called for 20 monthly payments of $1025 each. Find (a) the finance charge, __________ (b) the unearned interest, __________ and (c) the amount necessary to pay the loan in full after the 14th payment. __________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
73
Use the loan payoff table to find the monthly payment (MP) and finance charge (FC) for each of the following loans. (See Example.)
Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
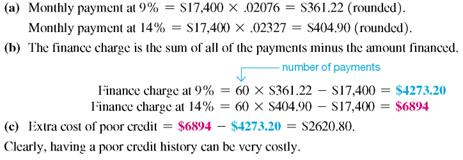

Finding Amortization Payments
After a trade-in, Vickie Ewing owes $17,400 on a new Harley-Davidson motorcycle and wishes to pay the loan off in 60 months. She has found that she can finance the loan at 9% per year if she has a good credit history, but at 14, per year if she has a poor credit history.
(a) Find the monthly payment at both interest rates.
(b) Find the total finance charge at both interest rates.
(c) Find the extra cost of having poor credit.
SOLUTION
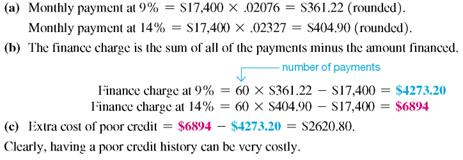


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
74
Use the real estate amortization table to find the monthly payment for the following loans. (See Example 1.)



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
75
Find the annual percentage rate, using the annual percentage rate table.



Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the following application problems using 360-day years where applicable.
A public utility needs $60 million in 5 years for a major capital expansion. What annual payment must the firm place into a sinking fund earning 10 per year in order to accumulate the required funds?
A public utility needs $60 million in 5 years for a major capital expansion. What annual payment must the firm place into a sinking fund earning 10 per year in order to accumulate the required funds?

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
77
Explain the terms present value, future value , and annuity.

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the following application problems.
HOT TUB PURCHASE Betty Thomas borrowed $6500 on her Visa card to install a hot tub with landscaping around it. The interest charges are 1.6% per month on the unpaid balance. (a) Find the interest charges. __________ (b) Find the interest charges if she moves the debt to a credit card charging 1% per month on the unpaid balance. __________ (c) Find the monthly savings.__________

HOT TUB PURCHASE Betty Thomas borrowed $6500 on her Visa card to install a hot tub with landscaping around it. The interest charges are 1.6% per month on the unpaid balance. (a) Find the interest charges. __________ (b) Find the interest charges if she moves the debt to a credit card charging 1% per month on the unpaid balance. __________ (c) Find the monthly savings.__________


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
79
Find the approximate annual percentage rate using the approximate annual percentage rate formula. Round to the nearest tenth of a percent. (See Example.)
Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
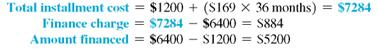
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.

Finding the Annual Percentage Rate
Ed Chamski decides to buy a used car for $6400. He makes a down payment of $1200 and monthly payments of $169 for 36 months. Find the approximate annual percentage rate rounded to the nearest tenth of a percent.
SOLUTION
Use the steps outlined above.
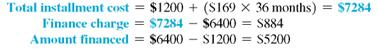
Quick TIP
The precise APR can be found using a financial calculator as shown in examples in Appendix C.
Use the formula for approximate APR. Replace the finance charge with $884, the amount financed with $5200, and the number of payments with 36.

The approximate annual percentage rate on this loan is 11%. Example shows how to find the actual APR for this loan.
Finding the Annual Percentage Rate
In Example, a used car costing $6400 was financed at $169 per month for 36 months after a down payment of $1200. The total finance charge was $884, and the amount financed was $5200. Find the annual percentage rate.
SOLUTION
Step 1 Multiply the finance charge by $100, and divide by the amount financed.
Quick TIP
When using the annual percentage rate table, select the column with the table number that is closest to the finance charge per $100 of amount financed.

This gives the finance charge per $100 financed.
Step 2 Read down the left column of the annual percentage rate table to the line for 36 months (the actual number of monthly payments). Follow across to the right to find the number closest to $17.00. Here, find 17.01. Read the number at the top of this column of figures to find the annual percentage rate, 10.50%.
In this example, 10.50% is the annual percentage rate that must be disclosed to the buyer of the car. In Example, the formula for the approximate annual percentage rate gave an answer of 11%, which is not accurate enough to meet the requirements of the law.


Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the following application problems and use the table to find the annual percentage rate.
REFRIGERATOR PURCHASE Sears offers a refrigerator for $1600 with no down payment, $294.06 in interest charges, and 30 equal payments. Find the annual percentage rate. _________
REFRIGERATOR PURCHASE Sears offers a refrigerator for $1600 with no down payment, $294.06 in interest charges, and 30 equal payments. Find the annual percentage rate. _________

Unlock Deck
Unlock for access to all 168 flashcards in this deck.
Unlock Deck
k this deck


