Deck 3: Kinetic Concepts for Analyzing Human Motion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/20
Play
Full screen (f)
Deck 3: Kinetic Concepts for Analyzing Human Motion
1
What is the volume of a milk crate with sides of 25 cm, 40 cm, and 30 cm?
Find the area of the object. The dimensions of the object are 25 cm, 40 cm, and 30 cm.
The volume of a box can be calculated using the formula for volume. Volume V is length l multiplied by width w multiplied by height h.
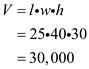 The volume of the object is 30,000 cm 3.
The volume of the object is 30,000 cm 3.
The volume of a box can be calculated using the formula for volume. Volume V is length l multiplied by width w multiplied by height h.
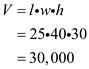 The volume of the object is 30,000 cm 3.
The volume of the object is 30,000 cm 3. 2
Estimate the volume of your own body. Construct a table that shows the approximate body dimensions you used in formulating your estimate.
To estimate the volume of the average human body, the limbs, torso and head must be divided and estimated.
All limbs and have a cylindrical shape, thus the equation for volume of a cylinder will be used. Volume of a cylinder is pi multiplied by the radius r squared multiplied by height.
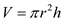 The torso is more of a box shape, thus using the formula length l multiplied by width w multiplied by height h will be used.
The torso is more of a box shape, thus using the formula length l multiplied by width w multiplied by height h will be used.
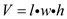 The head is shaped like a sphere, thus the formula for the volume of a sphere will be used. The volume of a sphere can be calculated by multiplying 4/3 by pi multiplied by the radius r cubed.
The head is shaped like a sphere, thus the formula for the volume of a sphere will be used. The volume of a sphere can be calculated by multiplying 4/3 by pi multiplied by the radius r cubed.
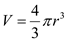
 Total calculated volume can be found by adding all of the objects calculated volumes together. Since the human body has two legs and two arms, these volumes must be doubled.
Total calculated volume can be found by adding all of the objects calculated volumes together. Since the human body has two legs and two arms, these volumes must be doubled.
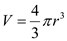 The total calculated volume of the human body is estimated to be 1648.7 in 3.
The total calculated volume of the human body is estimated to be 1648.7 in 3.
All limbs and have a cylindrical shape, thus the equation for volume of a cylinder will be used. Volume of a cylinder is pi multiplied by the radius r squared multiplied by height.
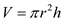 The torso is more of a box shape, thus using the formula length l multiplied by width w multiplied by height h will be used.
The torso is more of a box shape, thus using the formula length l multiplied by width w multiplied by height h will be used. 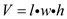 The head is shaped like a sphere, thus the formula for the volume of a sphere will be used. The volume of a sphere can be calculated by multiplying 4/3 by pi multiplied by the radius r cubed.
The head is shaped like a sphere, thus the formula for the volume of a sphere will be used. The volume of a sphere can be calculated by multiplying 4/3 by pi multiplied by the radius r cubed. 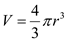
 Total calculated volume can be found by adding all of the objects calculated volumes together. Since the human body has two legs and two arms, these volumes must be doubled.
Total calculated volume can be found by adding all of the objects calculated volumes together. Since the human body has two legs and two arms, these volumes must be doubled. 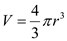 The total calculated volume of the human body is estimated to be 1648.7 in 3.
The total calculated volume of the human body is estimated to be 1648.7 in 3. 3
Choose three objects that are within your field of view, and estimate the volume of each. List the approximate dimensions you used in formulating your estimates.
To determine the approximate volume of a crate, the lengths of the sides of the crate must be estimated, and then multiplied together. The sides all look to be approximately 5 inches in length. Volume V is length l multiplied by width w multiplied by height h.
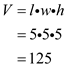 The approximate volume of the object is 125 in 3.
The approximate volume of the object is 125 in 3.
To determine the approximate volume of a coffee mug, the height of the coffee mug and the approximate radius must be estimated. The height looks to be three inches and the radius looks to be 1 inch. Volume of a cylinder V is pi multiplied by radius r squared and the height.

 The approximate volume of the mug is 9.4 in 3.
The approximate volume of the mug is 9.4 in 3.
To determine the approximate volume of a drinking glass, the height of the glass and the approximate radius must be estimated. The height looks to be five inches and the radius looks to be 1 inch. Volume of a cylinder V is pi multiplied by radius r squared and the height.

 The approximate volume of the mug is 15.7 in 3.
The approximate volume of the mug is 15.7 in 3.
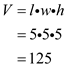 The approximate volume of the object is 125 in 3.
The approximate volume of the object is 125 in 3.To determine the approximate volume of a coffee mug, the height of the coffee mug and the approximate radius must be estimated. The height looks to be three inches and the radius looks to be 1 inch. Volume of a cylinder V is pi multiplied by radius r squared and the height.

 The approximate volume of the mug is 9.4 in 3.
The approximate volume of the mug is 9.4 in 3.To determine the approximate volume of a drinking glass, the height of the glass and the approximate radius must be estimated. The height looks to be five inches and the radius looks to be 1 inch. Volume of a cylinder V is pi multiplied by radius r squared and the height.

 The approximate volume of the mug is 15.7 in 3.
The approximate volume of the mug is 15.7 in 3. 4
What is your own body mass in kg?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
5
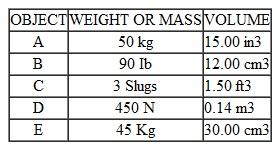
Given the mass or weight and the volume of each of the following objects, rank them in the order of their densities.


Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
6
William Perry, defensive tackle and part-time running back better known as "The Refrigerator," weighed in at 1352 N during his 1985 rookie season with the Chicago Bears. What was Perry's mass?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
7
If the contents of the crate described in Problem 7 weigh 120 N, what are the average density and specific weight of the box and contents?
Problem 7
What is the volume of a milk crate with sides of 25 cm, 40 cm, and 30 cm?
Problem 7
What is the volume of a milk crate with sides of 25 cm, 40 cm, and 30 cm?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
8
Gravitational force on planet X is 40% of that found on the earth. If a person weighs 667.5 N on earth, what is the person's weight on planet X? What is the person's mass on the earth and on planet X?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
9
Two muscles develop tension simultaneously on opposite sides of a joint. Muscle A, attaching 3 cm from the axis of rotation at the joint, exerts 250 N of force. Muscle B, attaching 2.5 cm from the joint axis, exerts 260 N of force. How much torque is created at the joint by each muscle? What is the net torque created at the joint? In which direction will motion at the joint occur?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
10
How much force must be applied to a 0.5 kg hockey puck to give it an acceleration of 30 m/s 2 ?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
11
Two children sit on opposite sides of a playground seesaw. Joey, who weighs 220 N, sits 1.5 m from the axis of the seesaw, and Suzy, who weighs 200 N, sits 1.7 m from the axis of the seesaw. How much torque is created at the axis by each child? In which direction will the seesaw tip?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
12
A football player is contacted by two tacklers simultaneously. Tackler A exerts a force of 400 N, and tackler B exerts a force of 375 N. If the forces are coplanar and directed perpendicular to each other, what is the magnitude and direction of the resultant force acting on the player?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
13
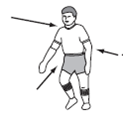
A rugby player is contacted simultaneously by three opponents who exert forces of the magnitudes and directions shown in the diagram at right. Using a graphic solution, show the magnitude and direction of the resultant force.


Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
14
A 75 kg skydiver in free fall is subjected to a crosswind exerting a force of 60 N and to a vertical air resistance force of 100 N. Describe the resultant force acting on the skydiver.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
15
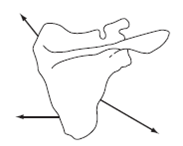
Using a graphic solution, compose the muscle force vectors to find the net force acting on the scapula shown below.


Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
16
Use a trigonometric solution to find the magnitude of the resultant of the following coplanar forces: 60 N at 90°, 80 N at 120°, and 100 N at 270°.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
17
Draw the horizontal and vertical components of the vectors shown below.



Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
18
If 37% of body weight is distributed above the superior surface of the L5 intervertebral disc and the area of the superior surface of the disc is 25 cm 2 , how much pressure exerted on the disc is attributable to body weight for a 930 N man?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
19
A gymnastics floor mat weighing 220 N has dimensions of 3 m × 4 m × 0.04 m. How much pressure is exerted by the mat against the floor?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
20
In the nucleus pulposus of an intervertebral disc, the compressive load is 1.5 times the externally applied load. In the annulus fibrosus, the compressive force is 0.5 times the external load. What are the compressive loads on the nucleus pulposus and annulus fibrosus of the L5-S1 intervertebral disc of a 930 N man holding a 445 N weight bar across his shoulders, given that 37% of body weight is distributed above the disc?

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck


