Deck 17: Behavioral Economics
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/37
Play
Full screen (f)
Deck 17: Behavioral Economics
1
Use a calculator to verify the value of the second prize offered by the queen.
2. Suppose the queen offers a third prize. This prize starts at $10,000 on the first day, doubling every other day over a 31-day month. Before doing any calculations, guess whether the hero should choose this prize. Check your guess by calculating the exact prize value.
2. Suppose the queen offers a third prize. This prize starts at $10,000 on the first day, doubling every other day over a 31-day month. Before doing any calculations, guess whether the hero should choose this prize. Check your guess by calculating the exact prize value.
1. In accordance with the second prize, the hero will get one penny for the first day, two penny on the second day, four penny on the third day and so on for a month of 31 days. Thus, the total value of the prize will be
 Hence, it can be seen that the value of the second prize is
Hence, it can be seen that the value of the second prize is
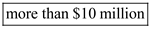 .
.
2. As per the terms of the third prize, the hero recieves $10,000 on the first day, $20,000 on the third day, $40,000 on the fifth day and so on for a month of 31 days. At the face value, the hero will not choose the prize because it will appear to him that the thrid prize is less than the first prize. However, the calculation shows that the hero should choose the third prize over first prize because it will pay him $328 million over the 31 days. The calculation is shown below:
 or
or
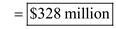
 Hence, it can be seen that the value of the second prize is
Hence, it can be seen that the value of the second prize is 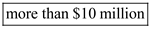 .
.2. As per the terms of the third prize, the hero recieves $10,000 on the first day, $20,000 on the third day, $40,000 on the fifth day and so on for a month of 31 days. At the face value, the hero will not choose the prize because it will appear to him that the thrid prize is less than the first prize. However, the calculation shows that the hero should choose the third prize over first prize because it will pay him $328 million over the 31 days. The calculation is shown below:
 or
or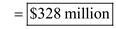
2
A queen gives a dragon-slaying hero a choice between two prizes. The first provides $100,000 a day for d days; the second provides an amount of money that doubles in size each day for d days starting from a penny (so one penny the first day, two pennies the second, four pennies the next, etc.).
a. Provide the formula for the amount of money after d days provided by each prize.
b. Graph your results for values of d ranging from 0 to 31 days.
c. Using your graph, advise the hero on which prize he should choose depending on the number of days d involved in the queen's offer.
a. Provide the formula for the amount of money after d days provided by each prize.
b. Graph your results for values of d ranging from 0 to 31 days.
c. Using your graph, advise the hero on which prize he should choose depending on the number of days d involved in the queen's offer.
a) Since the first prize provides $100,000 for
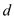 days, therefore the formula for the first prize is
days, therefore the formula for the first prize is
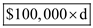 .
.
The second prize provides one penny on the first day and thereafter it doubles each day for d days. Since the amount of prize increases exponentially, therefore the formula will be
 .
.
b) Consider the graph given below
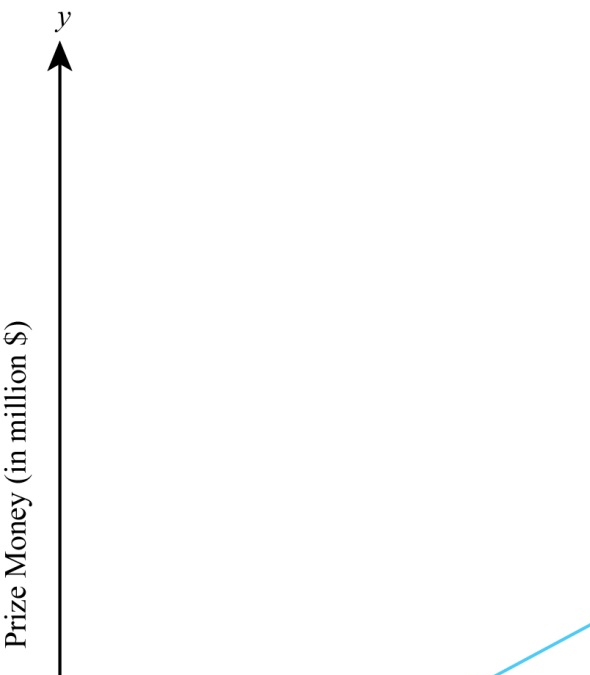 In the graph, the x -axis measures days
In the graph, the x -axis measures days
 and the
and the
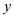 -axis measures money (in million $). Further the red line shows the first prize wherein the line of prize money increases at a constant rate and is upward sloping and linear. The blue line shows the second prize wherein the prize money line rises steeply after
-axis measures money (in million $). Further the red line shows the first prize wherein the line of prize money increases at a constant rate and is upward sloping and linear. The blue line shows the second prize wherein the prize money line rises steeply after
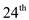 day indicating the exponential growth in the size of second prize.
day indicating the exponential growth in the size of second prize.
c) It can be seen from the above graph that the two lines cross between 29 and 30 days. It is advisable that the hero should choose the first prize if he is thinking of benefits in the short run. And if he is thinking of the long-run, then he is advised to choose the second prize.
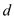 days, therefore the formula for the first prize is
days, therefore the formula for the first prize is 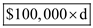 .
.The second prize provides one penny on the first day and thereafter it doubles each day for d days. Since the amount of prize increases exponentially, therefore the formula will be
 .
.b) Consider the graph given below
 In the graph, the x -axis measures days
In the graph, the x -axis measures days  and the
and the  -axis measures money (in million $). Further the red line shows the first prize wherein the line of prize money increases at a constant rate and is upward sloping and linear. The blue line shows the second prize wherein the prize money line rises steeply after
-axis measures money (in million $). Further the red line shows the first prize wherein the line of prize money increases at a constant rate and is upward sloping and linear. The blue line shows the second prize wherein the prize money line rises steeply after  day indicating the exponential growth in the size of second prize.
day indicating the exponential growth in the size of second prize.c) It can be seen from the above graph that the two lines cross between 29 and 30 days. It is advisable that the hero should choose the first prize if he is thinking of benefits in the short run. And if he is thinking of the long-run, then he is advised to choose the second prize.
3
Describe the three limits to rational decision making identified in this chapter.
Behavioral economics identifies three limits that restrict the ability of individuals to make a rational decision or a payoff-maximizing decision. These limits are:
i) Limited cognitive ability: This relates to an individual's limitations in calculating the payoffs when the decision-making involved is complex.
ii) Limited willpower: This limitation is important in dynamic decisions. These are decisions that involve some time element, where an action taken has long-term implications.
iii) Limited self-interest: This limitation relates to the fact that sometimes people are not driven by self-interest. Rather, interpersonal values are also important to individuals to determine fairness.
i) Limited cognitive ability: This relates to an individual's limitations in calculating the payoffs when the decision-making involved is complex.
ii) Limited willpower: This limitation is important in dynamic decisions. These are decisions that involve some time element, where an action taken has long-term implications.
iii) Limited self-interest: This limitation relates to the fact that sometimes people are not driven by self-interest. Rather, interpersonal values are also important to individuals to determine fairness.
4
On a graph similar to Figure, demonstrate that the person with standard, risk-averse preferences would choose B or D over the other gambles in the two Kahneman and Tversky scenarios.
Figure Standard Preferences versus Prospect Theory
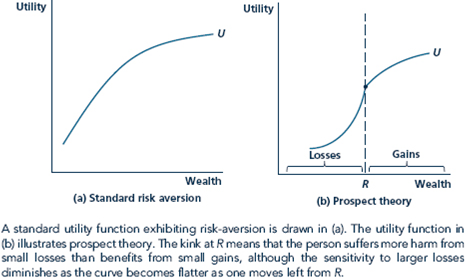
Figure Standard Preferences versus Prospect Theory


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
5
Imagine that you are a subject in one of Maurice Allais lab experiments involving the same four gambles as in the chapter. Gamble A provides a 89% chance of winning $1,000, a 10% chance of winning $5,000, and a 1% chance of winning nothing. Gamble B provides a 100% chance of winning $1,000. Gamble C provides an 11% chance of winning $1,000 and an 89% chance of winning nothing. Finally, gamble D provides a 10% chance of winning $5,000 and a 90% chance of winning nothing. Your utility function over money is U(x) = \Jx.
a. Compute your expected utility from each of the four gambles.
b. In the first scenario, you are given a choice between gambles A and B. Which would you choose given your utility function?
c. In the second scenario, you are given a choice between gambles C and D. Which would you choose given your utility function?
d. Compare your choices in the two scenarios, and compare them to the actual experimental results reported in the text.
a. Compute your expected utility from each of the four gambles.
b. In the first scenario, you are given a choice between gambles A and B. Which would you choose given your utility function?
c. In the second scenario, you are given a choice between gambles C and D. Which would you choose given your utility function?
d. Compare your choices in the two scenarios, and compare them to the actual experimental results reported in the text.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
6
Distinguish between behavioral and neoclassical economics. What are the relative merits of each approach? Would you expect the relative merits to change as knowledge advances?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
7
According to a recent poll, 61% of citizens approve of an elected official's performance, and 39% disapprove.
1. How would a political supporter like to see these poll results reported?
2. How would a political enemy like to see these poll results reported?
1. How would a political supporter like to see these poll results reported?
2. How would a political enemy like to see these poll results reported?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
8
Refer back to Chapter 5, in particular to the Prisoners' Dilemma in Figure. Imagine that these payoffs are monetary payoffs, with negative numbers being money that is taken away from a player.
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. Find the pure-strategy Nash equilibria.
b. Suppose that players have a preference for fairness. Each player loses 1 util for each dollar difference (in absolute value) between their payoffs. Show how the Prisoners' Dilemma payoffs would change by writing down a new normal form. Find the pure-strategy Nash equilibria.
c. Suppose that players have different fairness preferences than in part b. Suppose that only the player who earns less money cares about fairness. That player loses 1 util for each dollar less he or she earns than the other player. Write down the normal form of the Prisoners' Dilemma reflecting these new preferences. Find the pure-strategy Nash equilibria.
Figure Prisoner's Dilemma in Extensive From
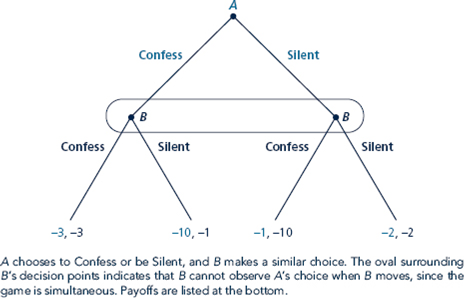
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. Find the pure-strategy Nash equilibria.
b. Suppose that players have a preference for fairness. Each player loses 1 util for each dollar difference (in absolute value) between their payoffs. Show how the Prisoners' Dilemma payoffs would change by writing down a new normal form. Find the pure-strategy Nash equilibria.
c. Suppose that players have different fairness preferences than in part b. Suppose that only the player who earns less money cares about fairness. That player loses 1 util for each dollar less he or she earns than the other player. Write down the normal form of the Prisoners' Dilemma reflecting these new preferences. Find the pure-strategy Nash equilibria.
Figure Prisoner's Dilemma in Extensive From


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
9
One oddity often observed in the market is that stores charge prices ending in 99 (so we see prices of $1.99, $5.99, and so forth). Explain why this sort of pricing might be puzzling to economists. Some have suggested that this is due to stores trying to exploit a cognitive limitation of shoppers. What sort of cognitive limitation might this be? Would you expect market forces to prevent firms from exploiting consumers in this or other ways?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
10
Instead of playing an equilibrium, suppose player 1 believes that 2 chooses C in the last stage with a certain probability. What would this probability have to be for 1 to choose C rather than E in the next-to-last stage?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
11
Refer back to Chapter 5, in particular to the Battle of the Sexes in Table Imagine that these payoffs are monetary payoffs.
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. What are the pure-strategy Nash equilibria?
b. Suppose that players have extreme preferences for fairness. Each player loses 10 utils for each dollar difference (in absolute value) between their payoffs. Show how the payoffs in the Battle of the Sexes would change by writing down a new normal form. Find the pure-strategy Nash equilibria.
c. Suppose that players have different fairness preferences than in part b. Now only the player who earns more money cares about fairness. This player feels guilty about earning more, losing 10 utils for each dollar advantage. Write down the normal form of the Battle of the Sexes reflecting these new preferences. Find the pure-strategy Nash equilibria.
Table Battle of the Sexes in Normal Form
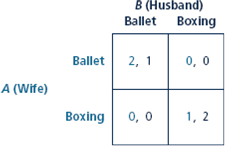
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. What are the pure-strategy Nash equilibria?
b. Suppose that players have extreme preferences for fairness. Each player loses 10 utils for each dollar difference (in absolute value) between their payoffs. Show how the payoffs in the Battle of the Sexes would change by writing down a new normal form. Find the pure-strategy Nash equilibria.
c. Suppose that players have different fairness preferences than in part b. Now only the player who earns more money cares about fairness. This player feels guilty about earning more, losing 10 utils for each dollar advantage. Write down the normal form of the Battle of the Sexes reflecting these new preferences. Find the pure-strategy Nash equilibria.
Table Battle of the Sexes in Normal Form


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
12
Behavioral economists have different views of the anomalies uncovered by experiments. Some view the anomalies as evidence of mistakes in decision making. Others view the anomalies as providing a new understanding of people's true preferences. What difference does it make for policy which theory is right? How could the theories be tested apart using experiments?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
13
The example shows that the hyperbolic discounter does not carry through on a plan to study when studying costs 20 utils. For what cost level would this same person carry through on a study plan?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
14
Refer to the Ultimatum Game in Figure. Recall that the payoffs are monetary payoffs.
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. Find the subgame-perfect equilibrium.
b. Suppose that players are imperfectly altruistic. They receive 1 util for each dollar they earn but

util for each dollar the other player earns. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium.
c. Suppose that players are perfectly altruistic, receiving 1 util for each dollar in the sum of their earnings. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium.
d. Suppose that players are perfectly selfless, getting 1 util for each dollar the other player earns but no utility for their own earnings. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium. Does player 1 end up choosing the outcome that player 2 prefers?
Figure Ultima tum Game
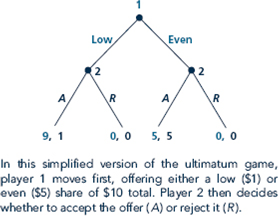
a. Suppose that players only care about monetary payoffs, with $1 - 1 util. Find the subgame-perfect equilibrium.
b. Suppose that players are imperfectly altruistic. They receive 1 util for each dollar they earn but

util for each dollar the other player earns. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium.
c. Suppose that players are perfectly altruistic, receiving 1 util for each dollar in the sum of their earnings. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium.
d. Suppose that players are perfectly selfless, getting 1 util for each dollar the other player earns but no utility for their own earnings. Write down the extensive form reflecting the new payoffs. Find the subgame-perfect equilibrium. Does player 1 end up choosing the outcome that player 2 prefers?
Figure Ultima tum Game


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
15
According to prospect theory, people are very averse to small risks. How is this captured on a utility function? How is this different from the standard theory about choice under uncertainty discussed in Chapter 4?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
16
Return to the Centipede Game (Figure). Assume now that in addition to caring about monetary payoffs, both players have a preference for fairness in that they lose 1 util for each dollar gap between the their payoffs (in absolute value).
1. Write down the extensive form for this new game.
2. Find the equilibrium. Can fairness provide another explanation of the experimental behavior in the Centipede Game cited earlier in the chapter?
Figure Centipede Game
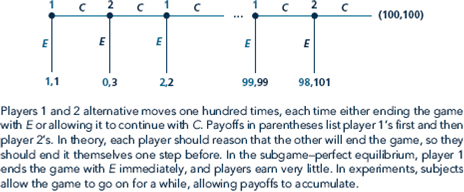
1. Write down the extensive form for this new game.
2. Find the equilibrium. Can fairness provide another explanation of the experimental behavior in the Centipede Game cited earlier in the chapter?
Figure Centipede Game


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
17
Julia visits her local grocery store to buy a jar of jam. She is overwhelmed to see the twenty-four varieties shown in Figure there.
a. Suppose she makes her decision by evaluating every pairwise comparison among the twenty-four varieties. How many comparisons does she have to make, and how long will it take her if she requires 1 second for each comparison?
b. Suppose she uses a different system for making her decision. First, she considers each of the separate categories separately and m the pair-wise comparisons just within the category to find the best. Then, she takes the best from each category and makes all the pairwise comparisons among them. Has she reduced the number of comparisons and total decision time using this system?
Figure Classifying Jame to Solve the Paradox of Choice
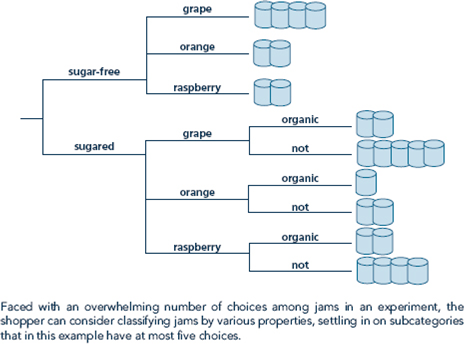
a. Suppose she makes her decision by evaluating every pairwise comparison among the twenty-four varieties. How many comparisons does she have to make, and how long will it take her if she requires 1 second for each comparison?
b. Suppose she uses a different system for making her decision. First, she considers each of the separate categories separately and m the pair-wise comparisons just within the category to find the best. Then, she takes the best from each category and makes all the pairwise comparisons among them. Has she reduced the number of comparisons and total decision time using this system?
Figure Classifying Jame to Solve the Paradox of Choice


Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
18
Argue that in the Centipede Game, a player is better off being known to be short-sighted. Are there any other settings in which it would be useful to be known to have behavioral biases?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
19
Will and Becky are two college students who are planning on Sunday how much they will study on Monday for a test on Tuesday. Will weighs future utility the same as current utility. Becky is more impulsive. She puts weight 1 on current period utility but only weight w on utility earned in future periods where 0
a. Under what condition on s and b would Will plan to study for the test? What condition is required for him to carry through on his plan?
b. Under what conditions on s and b would Becky plan to study for the test? What condition is required for her to carry through on her plan?
a. Under what condition on s and b would Will plan to study for the test? What condition is required for him to carry through on his plan?
b. Under what conditions on s and b would Becky plan to study for the test? What condition is required for her to carry through on her plan?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
20
What did Odysseus's having himself tied to the mast indicate about the level of his rationality? Provide three other examples of commitment devices used in the real world.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
21
In period 1, Mr. Consistency and Mr. Hyperbola are each trying to come up with a plan for how much they will exercise in period 2. Exercise is less enjoyable than other leisure activities, leading to a loss of 100 in terms of period 2 utils. Exercise provides health benefits, realized in period 3, leading to a gain of 250 in terms of period 3 utils. They put the following weights on utilities each period:
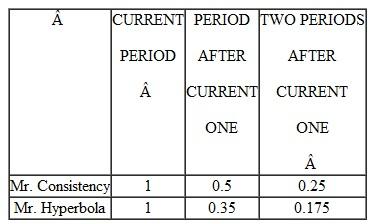
According to this table, Mr. Consistency's weight on future utility falls by half each period. Mr. Hyperbola's weights are related to Mr. Consistency's; the difference is that Mr. Hyperbola's are reduced a further 30% for periods after the current one.
a. Would Mr. Consistency plan to exercise in period 1? Would he follow through on this plan in period 2?
b. Show that Mr. Hyperbola would not follow through on his exercise plan.
c. Suppose Mr. Hyperbola could sign a contract in period 1 that forced him to give up an amount of money valued at x utils in period 2 if he does not stick with his exercise plan. How high would x have to be to help him commit to his plan?

According to this table, Mr. Consistency's weight on future utility falls by half each period. Mr. Hyperbola's weights are related to Mr. Consistency's; the difference is that Mr. Hyperbola's are reduced a further 30% for periods after the current one.
a. Would Mr. Consistency plan to exercise in period 1? Would he follow through on this plan in period 2?
b. Show that Mr. Hyperbola would not follow through on his exercise plan.
c. Suppose Mr. Hyperbola could sign a contract in period 1 that forced him to give up an amount of money valued at x utils in period 2 if he does not stick with his exercise plan. How high would x have to be to help him commit to his plan?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
22
Distinguish between altruism, fairness, and reciprocity. Suggest experiments related to the Ultimatum Game that could sort out how much each of these interpersonal values matter to subjects.

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
23
Prospect Pete's preferences are given by the following utility function. His wealth prior to taking a gamble serves as a reference point. He gains 1 util for each dollar of wealth in the reference point. A gain beyond this reference point is worth 1 util per dollar. A loss below this reference point subtracts off 2 utils per dollar. Faced with the choice between gambles, he will choose the one giving the highest expected utility. He has signed up to be a subject in an experiment. Before starting the experiment, his wealth is $10,000.
a. In a first experiment, he is given a choice between two gambles. Gamble A offers an even chance of winning $250 or losing $100. Gamble B provides $30 with certainty. Which gamble would he choose?
b. In a second experiment, he is given a $100 starting bonus. Then, he is given the choice between two different gambles. Gamble C offers an even chance of winning $150 or losing $200. Gamble D results in a loss of $70 with certainty. What choice would he make if he calculates his reference point including the $100 starting bonus? Would his choice change his reference point is his initial $10,000 wealth, meaning that he considers the $100 starting bonus as part of the amount he gets from the gambles?
c. Are Pete's choices in parts a and b the same as he would make if he only cared about the final wealth level he ends up with after the experiment?
a. In a first experiment, he is given a choice between two gambles. Gamble A offers an even chance of winning $250 or losing $100. Gamble B provides $30 with certainty. Which gamble would he choose?
b. In a second experiment, he is given a $100 starting bonus. Then, he is given the choice between two different gambles. Gamble C offers an even chance of winning $150 or losing $200. Gamble D results in a loss of $70 with certainty. What choice would he make if he calculates his reference point including the $100 starting bonus? Would his choice change his reference point is his initial $10,000 wealth, meaning that he considers the $100 starting bonus as part of the amount he gets from the gambles?
c. Are Pete's choices in parts a and b the same as he would make if he only cared about the final wealth level he ends up with after the experiment?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
24
A vast amount of information is available on Internet Web sites free of charge. The Web site author may just be altruistic. Give at least two other motives for Web sites to give away information. Which motives seem to best fit some of your favorite Web sites that give away free information?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
25
Trans-fatty potato chips are competitively supplied. The supply curve is
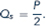
Demand for these potato chips is Q D = 100 - 2P.
a. Compute the equilibrium price, quantity, consumer surplus, producer surplus, and social welfare.
b. Suppose that consumers make irrational decisions either because of cognitive or willpower limitations, leading them to buy too many bags of potato chips. Although their true demand if they made rational decisions is as given already, their perceived or ''mistaken'' demand is Q D = 200 - 2P. Compute the equilibrium price and quantity now. Demonstrate the deadweight loss triangle on a diagram of the market and compute the deadweight loss.
c. What per-unit tax could the government impose to correct this deadweight loss problem?
d. Suppose instead the government made a mistake and the second demand is actually the true demand stemming from rational decisions. What deadweight loss has the government introduced with the tax?
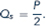
Demand for these potato chips is Q D = 100 - 2P.
a. Compute the equilibrium price, quantity, consumer surplus, producer surplus, and social welfare.
b. Suppose that consumers make irrational decisions either because of cognitive or willpower limitations, leading them to buy too many bags of potato chips. Although their true demand if they made rational decisions is as given already, their perceived or ''mistaken'' demand is Q D = 200 - 2P. Compute the equilibrium price and quantity now. Demonstrate the deadweight loss triangle on a diagram of the market and compute the deadweight loss.
c. What per-unit tax could the government impose to correct this deadweight loss problem?
d. Suppose instead the government made a mistake and the second demand is actually the true demand stemming from rational decisions. What deadweight loss has the government introduced with the tax?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
26
'Behavioral economics justifies intervention in the market by a paternalistic government.'' Explain the pros and cons of this view. What other market failures were identified in the book where government intervention might have been called for? Is the argument for intervening to solve behavioral problems stronger or weaker than the argument for intervening to solve these other market failures?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
27
One symptom of the recent U.S. economic crisis is the growing number of late mortgage payments and home foreclosures. Some blame predatory lenders, who induced naive consumers to sign complicated contracts (involving adjustable rates, balloon payments, and other features) with unfavorable terms that the consumers did not understand. Read some newspaper accounts of the Mortgage Reform and Anti-Predatory Lending Act, introduced into the U.S. House of Representatives in March 2009. What are potential costs and benefits of this bill? How much of the foreclosure problem can be attributed to consumer naivete versus an unexpected decline in economic conditions?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the fact that cold openings are becoming more common recently. Would this fact affect the signal you, as a fully rational and fully informed consumer, would take from cold opening now, compared to the past?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
29
There are a few cases in which movie studios cold open movies that go on to get fairly good reviews (for example, Snakes on a Plane, which opened in 2006). What do you think explain these cases?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
30
Do you think NFL coaching strategy will eventually change as a result of Romer's work? Does your prediction depend on the underlying reason why coaches were not following this strategy (mistakes versus preferences)?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
31
Imagine you are the coach of an NFLteam that is playing a much better opponent. How might this affect your decision to kick or ''go for it''?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
32
If you were designing a new lab experiment in economics, how many trials would you have subjects play to allow them to become familiar with the setting? On what factors would this depend? How could you determine what the ''right'' number of trials is?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
33
In the Oscar-winning movie Slumdog Millionaire, the hero of the movie, a contestant on a game show, is fed the wrong answer by the host to try to get him to lose.4 (The hero wisely chooses to ignore the host's ''hint.'') If Monty Hall has this same animosity toward contestants on Let's Make a Deal, how might this show up in when and whom to selects to offer the chance of switching? Would switching remain the correct decision for contestants? What if Monty is known instead to have a benevolent attitude toward contestants?
4 Slumdog Millionaire (Fox Searchlight, 2008)
4 Slumdog Millionaire (Fox Searchlight, 2008)

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
34
Whom would you select to ''referee'' your commitment contract? What would be the drawbacks of selecting a friend to ''referee'' the commitment contract? What about an enemy?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
35
Which self-control problems would be easiest to specify in a contract and have a ''referee'' monitor? Which problems would be difficult to monitor?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
36
What would happen to the number of late pickups if the fine were increased from $5 to $6? What if it were increased to $50 or even $500? How might the graph look if average number of late pickups (on the vertical axis) were plotted against the level of the late fine (on the horizontal axis).

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck
37
Think of some examples from your personal experience of situations where small fines were applied for ''bad'' behavior or small bonuses for ''good'' behavior. Did the prices have the anticipated effect or a perverse effect on behavior in these situations?

Unlock Deck
Unlock for access to all 37 flashcards in this deck.
Unlock Deck
k this deck


