Deck 11: Equilibrium and Elasticity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 11: Equilibrium and Elasticity
1
Simple harmonic motion: An object is undergoing simple harmonic motion with frequency f = 9.7 Hz and an amplitude of 0.12 m. At t = 0.00 s the object is at x = 0.00 m. How long does it take the object to go from 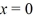 .00 m to
.00 m to 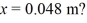
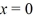 .00 m to
.00 m to 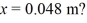
0.0068 seconds
2
Simple pendulum: A frictionless pendulum released from 65 degrees with the vertical will vibrate with the same frequency as if it were released from 5 degrees with the vertical because the period is independent of the amplitude and mass.
False
3
Simple harmonic motion: A sewing machine needle moves up and down in simple harmonic motion with an amplitude of 1.27 cm and a frequency of 2.55 Hz.
(a) What is the maximum speed of the needle?
(b) What is the maximum acceleration of the needle?
(a) What is the maximum speed of the needle?
(b) What is the maximum acceleration of the needle?
(a) 20.3 cm/s
(b) 326 cm/s2
(b) 326 cm/s2
4
Simple harmonic motion: The position of an object that is oscillating on an ideal spring is given by the equation x = (12.3 cm) cos[(1.26s-1)t]. At time t = 0.815 s,
(a) how fast is the object moving?
(b) what is the magnitude of the acceleration of the object?
(a) how fast is the object moving?
(b) what is the magnitude of the acceleration of the object?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
Simple harmonic motion: An object is executing simple harmonic motion. What is true about the acceleration of this object? (There may be more than one correct choice.)
A) The acceleration is a maximum when the displacement of the object is a maximum.
B) The acceleration is a maximum when the speed of the object is a maximum.
C) The acceleration is a maximum when the displacement of the object is zero.
D) The acceleration is zero when the speed of the object is a maximum.
E) The acceleration is a maximum when the object is instantaneously at rest.
A) The acceleration is a maximum when the displacement of the object is a maximum.
B) The acceleration is a maximum when the speed of the object is a maximum.
C) The acceleration is a maximum when the displacement of the object is zero.
D) The acceleration is zero when the speed of the object is a maximum.
E) The acceleration is a maximum when the object is instantaneously at rest.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
Energy in SHM: In simple harmonic motion, the speed is greatest at that point in the cycle when
A) the magnitude of the acceleration is a maximum.
B) the displacement is a maximum.
C) the magnitude of the acceleration is a minimum.
D) the potential energy is a maximum.
E) the kinetic energy is a minimum.
A) the magnitude of the acceleration is a maximum.
B) the displacement is a maximum.
C) the magnitude of the acceleration is a minimum.
D) the potential energy is a maximum.
E) the kinetic energy is a minimum.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
Energy in SHM: If we double only the mass of a vibrating ideal mass-and-spring system, the mechanical energy of the system
A) increases by a factor of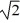 .
.
B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.
A) increases by a factor of
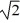 .
.B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
Simple pendulum: A certain frictionless simple pendulum having a length L and mass M swings with period T. If both L and M are doubled, what is the new period?
A) 4T
B) 2T
C)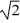 T
T
D) T
E) T/4
A) 4T
B) 2T
C)
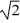 T
TD) T
E) T/4

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
Simple harmonic motion: A restoring force of magnitude F acts on a system with a displacement of magnitude x. In which of the following cases will the system undergo simple harmonic motion?
A) F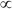
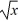
B) F sin x
sin x
C) F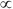 x2
x2
D) F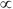 x
x
E) F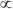 1/x
1/x
A) F
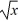
B) F
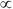 sin x
sin xC) F
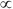 x2
x2D) F
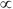 x
xE) F
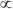 1/x
1/x
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
Energy in SHM: If we double only the amplitude of a vibrating ideal mass-and-spring system, the mechanical energy of the system
A) increases by a factor of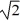 .
.
B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.
A) increases by a factor of
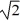 .
.B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Mass on a spring: A mass M is attached to an ideal massless spring. When this system is set in motion with amplitude A, it has a period T. What is the period if the amplitude of the motion is increased to 2A?
A) 2T
B) T/2
C)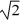 T
T
D) 4T
E) T
A) 2T
B) T/2
C)
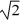 T
TD) 4T
E) T

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Simple pendulum: A frictionless pendulum clock on the surface of the earth has a period of 1.00 s. On a distant planet, the length of the pendulum must be shortened slightly to have a period of 1.00 s. What is true about the acceleration due to gravity on the distant planet?
A) The gravitational acceleration on the planet is slightly greater than g.
B) The gravitational acceleration on the planet is slightly less than g.
C) The gravitational acceleration on the planet is equal to g.
D) We cannot tell because we do not know the mass of the pendulum.
A) The gravitational acceleration on the planet is slightly greater than g.
B) The gravitational acceleration on the planet is slightly less than g.
C) The gravitational acceleration on the planet is equal to g.
D) We cannot tell because we do not know the mass of the pendulum.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Energy in SHM: If we double only the spring constant of a vibrating ideal mass-and-spring system, the mechanical energy of the system
A) increases by a factor of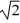 .
.
B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.
A) increases by a factor of
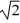 .
.B) increases by a factor of 2.
C) increases by a factor of 3.
D) increases by a factor of 4.
E) does not change.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Energy in SHM: An object is attached to a vertical ideal massless spring and bobs up and down between the two extreme points A and B. When the kinetic energy of the object is a minimum, the object is located
A) at either A or B.
B) midway between A and B.
C) 1/3 of the distance from A to B.
D) 1/4 of the distance from A to B.
E) 1/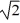 times the distance from A to B.
times the distance from A to B.
A) at either A or B.
B) midway between A and B.
C) 1/3 of the distance from A to B.
D) 1/4 of the distance from A to B.
E) 1/
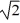 times the distance from A to B.
times the distance from A to B.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
Mass on a spring: A mass M is attached to an ideal massless spring. When this system is set in motion, it has a period T. What is the period if the mass is doubled to 2M?
A) 2T
B) T/2
C)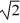 T
T
D) 4T
E) T
A) 2T
B) T/2
C)
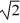 T
TD) 4T
E) T

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
Resonance: In designing buildings to be erected in an area prone to earthquakes, what relationship should the designer try to achieve between the natural frequency of the building and the typical earthquake frequencies?
A) The natural frequency of the building should be exactly the same as typical earthquake frequencies.
B) The natural frequency of the building should be very different from typical earthquake frequencies.
C) The natural frequency of the building should be almost the same as typical earthquake frequencies but slightly higher.
D) The natural frequency of the building should be almost the same as typical earthquake frequencies but slightly lower.
A) The natural frequency of the building should be exactly the same as typical earthquake frequencies.
B) The natural frequency of the building should be very different from typical earthquake frequencies.
C) The natural frequency of the building should be almost the same as typical earthquake frequencies but slightly higher.
D) The natural frequency of the building should be almost the same as typical earthquake frequencies but slightly lower.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
Simple harmonic motion: Which of following graphs describes simple periodic motion with amplitude 2.00 cm and angular frequency 2.00 rad/s?
A)
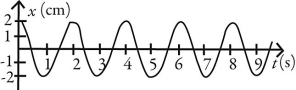
B)
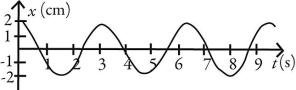
C)
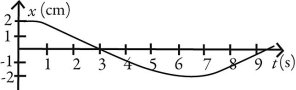
D)
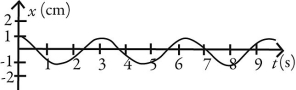
E)
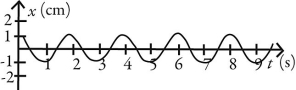
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
Simple harmonic motion: The simple harmonic motion of an object is described by the graph shown in the figure. What is the equation for the position x(t) of the object as a function of time t? ![<strong>Simple harmonic motion: The simple harmonic motion of an object is described by the graph shown in the figure. What is the equation for the position x(t) of the object as a function of time t? </strong> A) x(t) = (4.0 cm)sin[(2π/8.0 s)t + π/3.0] B) x(t) = (4.0 cm)cos[(2π/8.0 s)t + 2π/3.0] C) x(t) = (4.0 cm)cos[(2π/8.0 s)t + π/3.0] D) x(t) = (4.0 cm)cos[(2π/8.0 s)t - π/3.0] E) x(t) = (8.0 cm)cos[(2π/8.0 s)t + π/3.0]](https://storage.examlex.com/TB8274/11eb6b7b_2fb3_4807_b0cf_9938bb8c577d_TB8274_00.jpg)
A) x(t) = (4.0 cm)sin[(2π/8.0 s)t + π/3.0]
B) x(t) = (4.0 cm)cos[(2π/8.0 s)t + 2π/3.0]
C) x(t) = (4.0 cm)cos[(2π/8.0 s)t + π/3.0]
D) x(t) = (4.0 cm)cos[(2π/8.0 s)t - π/3.0]
E) x(t) = (8.0 cm)cos[(2π/8.0 s)t + π/3.0]
![<strong>Simple harmonic motion: The simple harmonic motion of an object is described by the graph shown in the figure. What is the equation for the position x(t) of the object as a function of time t? </strong> A) x(t) = (4.0 cm)sin[(2π/8.0 s)t + π/3.0] B) x(t) = (4.0 cm)cos[(2π/8.0 s)t + 2π/3.0] C) x(t) = (4.0 cm)cos[(2π/8.0 s)t + π/3.0] D) x(t) = (4.0 cm)cos[(2π/8.0 s)t - π/3.0] E) x(t) = (8.0 cm)cos[(2π/8.0 s)t + π/3.0]](https://storage.examlex.com/TB8274/11eb6b7b_2fb3_4807_b0cf_9938bb8c577d_TB8274_00.jpg)
A) x(t) = (4.0 cm)sin[(2π/8.0 s)t + π/3.0]
B) x(t) = (4.0 cm)cos[(2π/8.0 s)t + 2π/3.0]
C) x(t) = (4.0 cm)cos[(2π/8.0 s)t + π/3.0]
D) x(t) = (4.0 cm)cos[(2π/8.0 s)t - π/3.0]
E) x(t) = (8.0 cm)cos[(2π/8.0 s)t + π/3.0]

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Simple harmonic motion: A simple harmonic oscillator has an amplitude of 3.50 cm and a maximum speed of 26.0 cm/s. What is its speed when the displacement is 1.75 cm?
A) 12.0 cm/s
B) 22.5 cm/s
C) 14.2 cm/s
D) 15.0 cm/s
E) 17.0 cm/s
A) 12.0 cm/s
B) 22.5 cm/s
C) 14.2 cm/s
D) 15.0 cm/s
E) 17.0 cm/s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
Simple harmonic motion: The position x of an object varies with time t. For which of the following equations relating x and t is the motion of the object simple harmonic motion? (There may be more than one correct choice.)
A) x = 5 sin23t
B) x = 8 cos 3t
C) x = 4 tan 2t
D) x = 5 sin 3t
E) x = 2 cos(3t - 1)
A) x = 5 sin23t
B) x = 8 cos 3t
C) x = 4 tan 2t
D) x = 5 sin 3t
E) x = 2 cos(3t - 1)

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
Mass on a spring: A 0.28-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 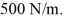 The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is
The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is 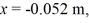 find the acceleration of the block.
find the acceleration of the block.
A) 92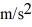
B) 46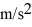
C) 69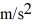
D) 230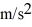
E) 280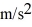
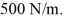 The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is
The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is 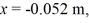 find the acceleration of the block.
find the acceleration of the block.A) 92
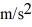
B) 46
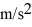
C) 69
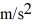
D) 230
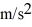
E) 280
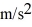

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
Energy in SHM: A 0.025-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 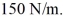 The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is
The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is 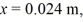 what is the kinetic energy of the block?
what is the kinetic energy of the block?
A) 0.44 J
B) 0.41 J
C) 0.46 J
D) 0.49 J
E) 0.52 J
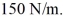 The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is
The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. When the displacement is 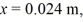 what is the kinetic energy of the block?
what is the kinetic energy of the block?A) 0.44 J
B) 0.41 J
C) 0.46 J
D) 0.49 J
E) 0.52 J

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
Mass on a spring: An object of mass 8.0 kg is attached to an ideal massless spring and allowed to hang in the Earth's gravitational field. The spring stretches 3.6 cm before it reaches its equilibrium position. If this system is allowed to oscillate, what will be its frequency?
A) 2.6 Hz
B) 0.0045 Hz
C) 0.67 Hz
D) 2.1 Hz
A) 2.6 Hz
B) 0.0045 Hz
C) 0.67 Hz
D) 2.1 Hz

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
Simple harmonic motion: The x component of the velocity of an object vibrating along the x-axis obeys the equation vx(t) = (0.445 m/s) sin[(25.4 rad/s)t + 0.223].
(a) What is the amplitude of the motion of this object?
(b) What is the maximum acceleration of the vibrating object?
(a) What is the amplitude of the motion of this object?
(b) What is the maximum acceleration of the vibrating object?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
Energy in SHM: A 1.5-kg mass attached to an ideal massless spring with a spring constant of 20.0 N/m oscillates on a horizontal, frictionless track. At time t = 0.00 s, the mass is released from rest at x = 10.0 cm. (That is, the spring is stretched by 10.0 cm.)
(a) Find the frequency of the oscillations.
(b) Determine the maximum speed of the mass. At what point in the motion does the maximum speed occur?
(c) What is the maximum acceleration of the mass? At what point in the motion does the maximum acceleration occur?
(d) Determine the total energy of the oscillating system.
(e) Express the displacement x as a function of time t.
(a) Find the frequency of the oscillations.
(b) Determine the maximum speed of the mass. At what point in the motion does the maximum speed occur?
(c) What is the maximum acceleration of the mass? At what point in the motion does the maximum acceleration occur?
(d) Determine the total energy of the oscillating system.
(e) Express the displacement x as a function of time t.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
Mass on a spring: An object that weighs 2.450 N is attached to an ideal massless spring and undergoes simple harmonic oscillations with a period of 0.640 s. What is the spring constant of the spring?
A) 2.45 N/m
B) 12.1 N/m
C) 24.1 N/m
D) 0.102 N/m
E) 0.610 N/m
A) 2.45 N/m
B) 12.1 N/m
C) 24.1 N/m
D) 0.102 N/m
E) 0.610 N/m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
Mass on a spring: A 2.25-kg object is attached to a horizontal an ideal massless spring on a frictionless table. What should be the spring constant of this spring so that the maximum acceleration of the object will be g when it oscillates with amplitude of 4.50 cm?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Simple harmonic motion: A machine part is vibrating along the x-axis in simple harmonic motion with a period of 0.27 s and a range (from the maximum in one direction to the maximum in the other) of 3.0 cm. At time t = 0 it is at its central position and moving in the +x direction. What is its position when t = 55 s?
A) x = -0.43 cm
B) x = -0.51 cm
C) x = +0.51 cm
D) x = -1.3 cm
E) x = -1.4 cm
A) x = -0.43 cm
B) x = -0.51 cm
C) x = +0.51 cm
D) x = -1.3 cm
E) x = -1.4 cm

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
Energy in SHM: A 0.25 kg ideal harmonic oscillator has a total mechanical energy of 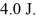 If the oscillation amplitude is
If the oscillation amplitude is 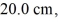 what is the oscillation frequency?
what is the oscillation frequency?
A) 4.5 Hz
B) 1.4 Hz
C) 2.3 Hz
D) 3.2 Hz
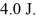 If the oscillation amplitude is
If the oscillation amplitude is 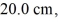 what is the oscillation frequency?
what is the oscillation frequency?A) 4.5 Hz
B) 1.4 Hz
C) 2.3 Hz
D) 3.2 Hz

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
Mass on a spring: A 1.6-kg block on a horizontal frictionless surface is attached to an ideal massless spring whose spring constant is 190 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a displacement x = +0.080 m and is released from rest. The block then executes simple harmonic motion along the horizontal x-axis. What is the velocity of the block at time t = 0.40 s?
A) 0.82 m/s
B) -0.82 m/s
C) 0.30 m/s
D) -0.30 m/s
E) 0.00 m/s
A) 0.82 m/s
B) -0.82 m/s
C) 0.30 m/s
D) -0.30 m/s
E) 0.00 m/s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
Mass on a spring: A 56.0 kg bungee jumper jumps off a bridge and undergoes simple harmonic motion. If the period of oscillation is 11.2 s, what is the spring constant of the bungee cord, assuming it has negligible mass compared to that of the jumper?
A) 17.6 N/m
B) 21.1 N/m
C) 28.2 N/m
A) 17.6 N/m
B) 21.1 N/m
C) 28.2 N/m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Energy in SHM: A 0.50-kg object is attached to an ideal massless spring of spring constant 20 N/m along a horizontal, frictionless surface. The object oscillates in simple harmonic motion and has a speed of 1.5 m/s at the equilibrium position.
(a) What is the amplitude of vibration?
(b) At what location are the kinetic energy and the potential energy of the system the same?
(a) What is the amplitude of vibration?
(b) At what location are the kinetic energy and the potential energy of the system the same?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
Mass on a spring: A 2.0 kg block on a frictionless table is connected to two ideal massless springs with spring constants k1 and k2 whose opposite ends are fixed to walls, as shown in the figure. What is angular frequency of the oscillation if 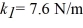 and
and 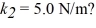
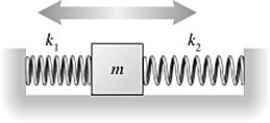
A) 2.5 rad/s
B) 3.5 rad/s
C) 0.40 rad/s
D) 0.56 rad/s
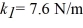 and
and 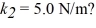

A) 2.5 rad/s
B) 3.5 rad/s
C) 0.40 rad/s
D) 0.56 rad/s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
Energy in SHM: An object of mass 6.8 kg is attached to an ideal massless spring of spring constant 1690 N/m. The object is pulled from its equilibrium position at x = 0.00 m to a displacement x = 0.35 m and is released from rest. Calculate the maximum speed the object reaches during its motion.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Energy in SHM: An object weighing 44.1 N hangs from a vertical massless ideal spring. When set in vertical motion, the object obeys the equation y(t) = (6.20 cm) cos[(2.74 rad/s)t - 1.40].
(a) Find the time for this object to vibrate one complete cycle.
(b) What are the maximum speed and maximum acceleration of the object.
(c) What is the TOTAL distance the object moves through in one cycle.
(d) Find the maximum kinetic energy of the object.
(e) What is the spring constant of the spring.
(a) Find the time for this object to vibrate one complete cycle.
(b) What are the maximum speed and maximum acceleration of the object.
(c) What is the TOTAL distance the object moves through in one cycle.
(d) Find the maximum kinetic energy of the object.
(e) What is the spring constant of the spring.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
Mass on a spring: In the figure, two masses, M = 16 kg and m = 12.8 kg, are connected to a very light rigid bar and are attached to an ideal massless spring of spring constant 100 N/m. The system is set into oscillation with an amplitude of 78 cm. At the instant when the acceleration is at its maximum, the 16-kg mass separates from the 12.8-kg mass, which then remains attached to the spring and continues to oscillate. What will be the amplitude of oscillation of the 12.8-kg mass? 
A) 78 cm
B) 62 cm
C) 35 cm
D) 98 cm
E) 180 cm

A) 78 cm
B) 62 cm
C) 35 cm
D) 98 cm
E) 180 cm

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Mass on a spring: A 2.00-kg object is attached to an ideal massless horizontal spring of spring constant 100.0 N/m and is at rest on a frictionless horizontal table. The spring is aligned along the x-axis and is fixed to a peg in the table. Suddenly this mass is struck by another 2.00-kg object traveling along the x-axis at 3.00 m/s, and the two masses stick together. What are the amplitude and period of the oscillations that result from this collision?
A) 0.300 m, 1.26 s
B) 0.300 m, 0.889 s
C) 0.424 m, 0.889 s
D) 0.424 m, 1.26 s
E) 0.424 m, 5.00 s
A) 0.300 m, 1.26 s
B) 0.300 m, 0.889 s
C) 0.424 m, 0.889 s
D) 0.424 m, 1.26 s
E) 0.424 m, 5.00 s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Simple pendulum: A frictionless simple pendulum on Earth has a period of 1.75 s. On Planet X its period is 2.14 s. What is the acceleration due to gravity on Planet X?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
Simple pendulum: In the figure, a 0.24-kg ball is suspended from a very light string 9.79 m long and is pulled slightly to the left. As the ball swings without friction through the lowest part of its motion it encounters an ideal massless spring attached to the wall. The spring pushes against the ball and eventually the ball is returned to its original starting position. Find the time for one complete cycle of this motion if the spring constant of the spring is 21 N/m. (Assume that once the pendulum ball hits the spring there is no effect due to the vertical movement of the ball.) 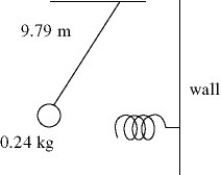


Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
Mass on a spring: A 12.0-N object is oscillating in simple harmonic motion at the end of an ideal vertical spring. Its vertical position y as a function of time t is given by y(t) = 4.50 cm cos[(19.5 s-1)t - π/8].
(a) What is the spring constant of the spring?
(b) What is the maximum acceleration of the object?
(c) What is the maximum speed that the object reaches?
(d) How long does it take the object to go from its highest point to its lowest point?
(a) What is the spring constant of the spring?
(b) What is the maximum acceleration of the object?
(c) What is the maximum speed that the object reaches?
(d) How long does it take the object to go from its highest point to its lowest point?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
Damped harmonic motion: A 25 kg object is undergoing lightly damped harmonic oscillations. If the maximum displacement of the object from its equilibrium point drops to 1/3 its original value in 1.8 s, what is the value of the damping constant b?
A) 31 kg/s
B) 34 kg/s
C) 37 kg/s
D) 40 kg/s
A) 31 kg/s
B) 34 kg/s
C) 37 kg/s
D) 40 kg/s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Damped harmonic motion: The amplitude of a lightly damped harmonic oscillator decreases from 60.0 cm to 40.0 cm in 10.0 s. What will be the amplitude of the harmonic oscillator after another 10.0 s passes?
A) 20.0 cm
B) 167 cm
C) 30.0 cm
D) 0.00 cm
E) 26.7 cm
A) 20.0 cm
B) 167 cm
C) 30.0 cm
D) 0.00 cm
E) 26.7 cm

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Physical pendulum: A uniform meter stick is freely pivoted about the 0.20-m mark. If it is allowed to swing in a vertical plane with a small amplitude and friction, what is the frequency of its oscillations?
A) 0.55 Hz
B) 0.66 Hz
C) 0.92 Hz
D) 1.1 Hz
E) 1.3 Hz
A) 0.55 Hz
B) 0.66 Hz
C) 0.92 Hz
D) 1.1 Hz
E) 1.3 Hz

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
Resonance: An object of mass of 2.0 kg hangs from an ideal massless spring with a spring constant of 50 N/m. An oscillating force F = (4.8 N) cos[(3.0 rad/s)t] is applied to the object. What is the amplitude of the resulting oscillations? You can neglect damping.
A) 0.15 m
B) 0.30 m
C) 1.6 m
D) 2.4 m
E) 0.80 m
A) 0.15 m
B) 0.30 m
C) 1.6 m
D) 2.4 m
E) 0.80 m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
Damped harmonic motion: A 5.0-kg block is attached to an ideal massless spring whose spring constant is 125 N/m. The block is pulled from its equilibrium position at x = 0.00 m to a position at x = +0.687 m and is released from rest. The block then executes lightly damped oscillation along the x-axis, and the damping force is proportional to the velocity. When the block first returns to x = 0.00 m, its x component of velocity is -2.0 m/s and its x component of acceleration is +5.6 m/s2.
(a) What is the magnitude of the acceleration of the block upon release at x = +0.687 m.
(b) Find the damping constant b.
(a) What is the magnitude of the acceleration of the block upon release at x = +0.687 m.
(b) Find the damping constant b.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Damped harmonic motion: An ideal massless spring with a spring constant of 2.00 N/m is attached to an object of 75.0 g. The system has a small amount of damping. If the amplitude of the oscillations decreases from 10.0 mm to 5.00 mm in 15.0 s, what is the magnitude of the damping constant b?
A) 0.00693 kg/s
B) 0.0462 kg/s
C) 0.00762 kg/s
D) 0.0100 kg/s
E) 0.00857 kg/s
A) 0.00693 kg/s
B) 0.0462 kg/s
C) 0.00762 kg/s
D) 0.0100 kg/s
E) 0.00857 kg/s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
Physical pendulum: A long thin uniform rod of length 1.50 m is to be suspended from a frictionless pivot located at some point along the rod so that its pendulum motion takes 3.00 s. How far from the center of the rod should the pivot be located?
A) 7.98 cm
B) 7.52 cm
C) 8.73 cm
D) 8.40 cm
E) 23.4 cm
A) 7.98 cm
B) 7.52 cm
C) 8.73 cm
D) 8.40 cm
E) 23.4 cm

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
Damped harmonic motion: A 2.15 kg lightly damped harmonic oscillator has an angular oscillation frequency of 0.261 rad/s. If the maximum displacement of  occurs when t = 0.00 s, and the damping constant b is 0.74 kg/s what is the object's displacement when t = 4.01 s?
occurs when t = 0.00 s, and the damping constant b is 0.74 kg/s what is the object's displacement when t = 4.01 s?
A) 0.50 m
B) 0.43 m
C) 0.58 m
D) 0.65 m
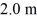 occurs when t = 0.00 s, and the damping constant b is 0.74 kg/s what is the object's displacement when t = 4.01 s?
occurs when t = 0.00 s, and the damping constant b is 0.74 kg/s what is the object's displacement when t = 4.01 s?A) 0.50 m
B) 0.43 m
C) 0.58 m
D) 0.65 m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
Damped harmonic motion: A lightly damped harmonic oscillator, with a damping force proportional to its speed, is oscillating with an amplitude of 0.500 cm at time t = 0. When t = 8.20 s, the amplitude has died down to 0.400 cm. At what value of t will the oscillations have an amplitude of 0.250 cm?
A) 18.5 s
B) 20.5 s
C) 16.5 s
D) 25.5 s
E) 5.13 s
A) 18.5 s
B) 20.5 s
C) 16.5 s
D) 25.5 s
E) 5.13 s

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Physical pendulum: A large stick is pivoted about one end and allowed to swing back and forth with no friction as a physical pendulum. The mass of the stick is 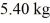 and its center of gravity (found by finding its balance point) is
and its center of gravity (found by finding its balance point) is 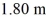 from the pivot. If the period of the swinging stick is
from the pivot. If the period of the swinging stick is 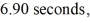 what is the moment of inertia of the stick about an axis through the pivot?
what is the moment of inertia of the stick about an axis through the pivot?
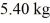 and its center of gravity (found by finding its balance point) is
and its center of gravity (found by finding its balance point) is 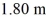 from the pivot. If the period of the swinging stick is
from the pivot. If the period of the swinging stick is 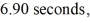 what is the moment of inertia of the stick about an axis through the pivot?
what is the moment of inertia of the stick about an axis through the pivot?
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


