Deck 7: Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/162
Play
Full screen (f)
Deck 7: Sampling Distributions
1
Small haphazard changes in a process variable due to alteration in the production environment that is not controllable are said to be assignable causes.
False
2
For a 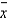 control chart, the lower and upper control limits are usually set at:
control chart, the lower and upper control limits are usually set at:
A) one standard deviation from the centerline
B) two standard deviations from the centerline
C) three standard deviations from the centerline
D) four standard deviations from the centerline
E) five standard deviations from the centerline
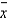 control chart, the lower and upper control limits are usually set at:
control chart, the lower and upper control limits are usually set at:A) one standard deviation from the centerline
B) two standard deviations from the centerline
C) three standard deviations from the centerline
D) four standard deviations from the centerline
E) five standard deviations from the centerline
three standard deviations from the centerline
3
If a process is in control, we expect all the data values to fall within three standard deviations of the mean.
True
4
Once a process is in control and is producing a satisfactory product, the process variables are monitored by use of control charts.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
5
The mean of the sample means and the standard deviation of 50 samples of size 5 taken from a production process under control are found to be 300 and 25, respectively. The lower control limit for the 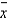 chart is located at:
chart is located at:
A) 333.54
B) 289.39
C) 310.61
D) 266.46
E) 342.88
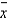 chart is located at:
chart is located at:A) 333.54
B) 289.39
C) 310.61
D) 266.46
E) 342.88

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
6
The first objective in statistical process control is to eliminate assignable causes of variation in the process variable and then get the process in control. The next step is to reduce variation and get the measurements on the process variable within specification limits, the limits within which the measurements on usable items or services must fall.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
7
If a process is in control, we expect all the data values to fall within two standard deviations of the mean.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
8
Assignable cause variation refers to variation in the output of a process that is naturally occurring, expected, and that may be the result of random causes.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
9
Random cause variation refers to variation n, the output of a process that is unexpected and has an assignable cause.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
10
Fifty samples of size 500 were drawn from a manufacturing process and the number of defectives in each sample was counted. The average of the sample proportion was 0.032. The centerline for the p chart is:
A) 0.032
B) 16.0
C) 0.512
D) 0.968
E) 4.2
A) 0.032
B) 16.0
C) 0.512
D) 0.968
E) 4.2

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
11
Twenty five samples of size 1000 each were drawn from a manufacturing process and the number of defectives in each sample was counted. The average sample proportion was 0.05. The upper control limit for the p chart is:
A) 0.0475
B) 0.0206
C) 0.0293
D) 0.0707
E) 0.0635
A) 0.0475
B) 0.0206
C) 0.0293
D) 0.0707
E) 0.0635

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
12
Random variation in a process can be eliminated.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
13
Process control charts, such as the 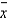 and p-charts, are used to provide signals to indicate when the output of a process is out of control.
and p-charts, are used to provide signals to indicate when the output of a process is out of control.
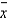 and p-charts, are used to provide signals to indicate when the output of a process is out of control.
and p-charts, are used to provide signals to indicate when the output of a process is out of control.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
14
Statistical process control (SPC) methodology was developed to monitor, control, and improve products and services.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
15
If a process is in control, we expect all the data values to fall within one standard deviation of the mean.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
16
In most processes, the process control limits are set to correspond with the specification limits on the process.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
17
The cause of a change in a process variable being monitored is regarded as random variation if it can be found and corrected.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
18
One of the most common sources of random cause variation is the people who are working in the process.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
19
In control process is typically defined as a process in which all output is operating within 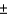 3 standard deviation of the centerline of the process.
3 standard deviation of the centerline of the process.
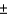 3 standard deviation of the centerline of the process.
3 standard deviation of the centerline of the process.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
20
If the variation in a process variable is solely random, the process is said to be in control.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
21
On a particular freeway in Michigan, it is reported that the proportion of cars that exceed the speed limit is 0.15. Given this information, the probability that a sample of 250 cars will have a sample proportion below 0.12 is approximately .0918.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
22
The standard error of the sampling distribution of sample proportion, SE ( 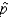 ), depends on the value of the population proportion p, and the closer the value of p to .50, the larger SE (
), depends on the value of the population proportion p, and the closer the value of p to .50, the larger SE ( 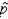 ) will be for a given sample size n.
) will be for a given sample size n.
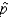 ), depends on the value of the population proportion p, and the closer the value of p to .50, the larger SE (
), depends on the value of the population proportion p, and the closer the value of p to .50, the larger SE ( 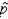 ) will be for a given sample size n.
) will be for a given sample size n.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
23
Standard error of the sample proportion is another term for the variance of the sampling distribution of the sample proportion 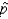 .
.
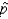 .
.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
24
A producer of brass rivets randomly samples 500 rivets each hour and calculates the proportion of defectives in the sample. The mean sample proportion calculated from 250 samples was equal to 0.025. Calculate the upper and lower control limits for a control chart for the proportion of defectives in samples of 500 rivets.
UCL = ______________
LCL = ______________
UCL = ______________
LCL = ______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
25
Assignable cause variation is also called:
A) random variation
B) special cause variation
C) common cause variation
D) within-group variation
E) none of these
A) random variation
B) special cause variation
C) common cause variation
D) within-group variation
E) none of these

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
26
Among the most common sources of random variation is:
A) people
B) materials
C) equipment
D) all of these
E) none of these
A) people
B) materials
C) equipment
D) all of these
E) none of these

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
27
Sixty samples of size 600 each were drawn from a manufacturing process and the number of defectives in each sample was counted. The average sample proportion was 0.04. The lower control limit for the p chart is:
A) 0.008
B) 0.016
C) 0.064
D) 0.048
E) 0.032
A) 0.008
B) 0.016
C) 0.064
D) 0.048
E) 0.032

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
28
Samples of n = 100 items were selected hourly over a 100-hour period, and the sample proportion of defectives was calculated each hour. The mean of the 100 sample proportions was 0.042.
Calculate the upper and lower control limits for a p chart.
UCL = ______________
LCL = ______________
Explain how to construct a p chart for the process and how it can be used.
________________________________________________________
Calculate the upper and lower control limits for a p chart.
UCL = ______________
LCL = ______________
Explain how to construct a p chart for the process and how it can be used.
________________________________________________________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
29
The Central Limit Theorem applies to the sampling distribution of sample proportion 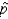 but not for the sampling distribution of sample mean
but not for the sampling distribution of sample mean 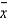 .
.
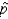 but not for the sampling distribution of sample mean
but not for the sampling distribution of sample mean 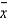 .
.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
30
As the sample size increases, the standard error of the sample proportion decreases.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
31
The expression SE ( 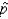 ) represents the standard error sampling distribution of the sample proportion,
) represents the standard error sampling distribution of the sample proportion, 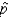 .
.
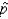 ) represents the standard error sampling distribution of the sample proportion,
) represents the standard error sampling distribution of the sample proportion, 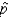 .
.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
32
A candy bar factory is pouring chocolate into molds to cool. The finished bars are sold as 1.25 ounce bars. The company will lose money if the molds are over-filled. If the molds are under-filled, the weight of the candy bars will be less than the wrapper label says, and the Food and Drug Administration will fine the company for misrepresenting the size of its product. The company wants to create an 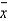 chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.
chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.
What is the centerline value?
______________
The calculated value of s, the sample standard deviation of all nk = (30)(5) = 150 observations, is 0.12 ounces. What is the standard error of the mean of 30 observations?
______________
What are the control limits?
UCL = ______________
LCL = ______________
How is the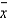 chart used in this situation?
chart used in this situation?
________________________________________________________
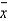 chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.
chart to monitor the weight of the candy bars. Suppose there are 5 samples of size 30 each taken, and their sample means are 1.27, 1.22, 1.26, 1.23, and 1.26 ounces.What is the centerline value?
______________
The calculated value of s, the sample standard deviation of all nk = (30)(5) = 150 observations, is 0.12 ounces. What is the standard error of the mean of 30 observations?
______________
What are the control limits?
UCL = ______________
LCL = ______________
How is the
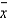 chart used in this situation?
chart used in this situation?________________________________________________________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
33
The mean of the sampling distribution of the sample proportion 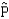 when n = 100 and p = 0.5 is 5.0.
when n = 100 and p = 0.5 is 5.0.
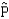 when n = 100 and p = 0.5 is 5.0.
when n = 100 and p = 0.5 is 5.0.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
34
As a general rule, the normal distribution is used to approximate the sampling distribution of the sample proportion only if the sample size n is greater than or equal to 30.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose that 56% of all registered voters in Michigan are supporting John Kerry for president. A sample of 1500 voters is selected at random from Michigan. Based on the concept of sampling distribution of sample proportion 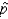 , it can be assumed that
, it can be assumed that 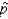 = .56.
= .56.
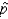 , it can be assumed that
, it can be assumed that 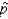 = .56.
= .56.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
36
Recall the rule of thumb used to indicate when the normal distribution is a good approximation of the sampling distribution for the sample proportion 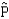 . For the combination n = 25; p = 0.05, the rule is satisfied.
. For the combination n = 25; p = 0.05, the rule is satisfied.
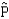 . For the combination n = 25; p = 0.05, the rule is satisfied.
. For the combination n = 25; p = 0.05, the rule is satisfied.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
37
The expression SE ( 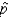 ) represents the standard deviation of the sampling distribution of the sample proportion,
) represents the standard deviation of the sampling distribution of the sample proportion, 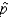 .
.
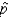 ) represents the standard deviation of the sampling distribution of the sample proportion,
) represents the standard deviation of the sampling distribution of the sample proportion, 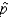 .
.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
38
The sampling distribution of the sample proportion 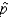 can be approximated by a normal distribution as long as the population proportion p is very close to .50.
can be approximated by a normal distribution as long as the population proportion p is very close to .50.
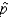 can be approximated by a normal distribution as long as the population proportion p is very close to .50.
can be approximated by a normal distribution as long as the population proportion p is very close to .50.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose an actual census showed that 20% of the households in Michigan have incomes in excess of $60,000. Assume that a random sample of 500 households in Michigan is taken. Then, the standard error of the sampling distribution of sample proportion of households who have incomes in excess of $60,000 will be:
A) 0.0179
B) 0.0003
C) 0.1600
D) 0.0256
E) 0.1482
A) 0.0179
B) 0.0003
C) 0.1600
D) 0.0256
E) 0.1482

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
40
The standard error of the sampling distribution of the sample proportion 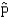 when n = 100 and p = 0.15 is 0.001275.
when n = 100 and p = 0.15 is 0.001275.
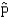 when n = 100 and p = 0.15 is 0.001275.
when n = 100 and p = 0.15 is 0.001275.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
41
A student government representative at a local university claims that 60% of the undergraduate students favor a move to Division I in college football. A random sample of 250 undergraduate students is selected.
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion exceeds 0.65.
______________
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion exceeds 0.65.
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
42
If the standard error of the sampling distribution of the sample proportion is 0.02049 for samples of size 500, then the population proportion must be either:
A) 0.2 or 0.8
B) 0.5 or 0.5
C) 0.3 or 0.7
D) 0.6 or 0.4
E) 0.2 or 0.5
A) 0.2 or 0.8
B) 0.5 or 0.5
C) 0.3 or 0.7
D) 0.6 or 0.4
E) 0.2 or 0.5

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
43
A candy bar company is interested in reducing the percent defective candy bars made, where a defective candy bar has too few almonds by weight. The company randomly samples 100 candy bars a day for 5 days and finds the percent defective to be 0.0200, 0.0125, 0.0225, 0.0100, and 0.0150. The company wants to construct a control chart for the proportion defective in samples of size n = 100.
Estimate the process fraction defective p.
______________
Estimate the standard deviation of the sample proportions.
______________
What are the control limits?
UCL = ______________
LCL = ______________
How are these control limits used?
________________________________________________________
Estimate the process fraction defective p.
______________
Estimate the standard deviation of the sample proportions.
______________
What are the control limits?
UCL = ______________
LCL = ______________
How are these control limits used?
________________________________________________________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
44
As a general rule, the normal distribution provides a good approximation to the sampling distribution of the sample proportion 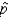 only if:
only if:
A) the sample size n is greater than 30
B) the sample size n is greater than 100
C) the population proportion p is greater than 0.50
D) the underlying population has a small standard deviation and n is large
E) np and n(1-p) are both greater than 5
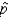 only if:
only if:A) the sample size n is greater than 30
B) the sample size n is greater than 100
C) the population proportion p is greater than 0.50
D) the underlying population has a small standard deviation and n is large
E) np and n(1-p) are both greater than 5

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following statements is true regarding the sampling distribution of sample proportion 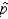 ?
?
A) The mean of the sampling distribution will equal the population proportion p.
B) The sampling distribution will be approximately normal provided that np > 5 and nq > 5.
C) An increase in the sample size n will result in a decrease in the standard error of.
D) All of these.
E) None of these.
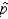 ?
?A) The mean of the sampling distribution will equal the population proportion p.
B) The sampling distribution will be approximately normal provided that np > 5 and nq > 5.
C) An increase in the sample size n will result in a decrease in the standard error of.
D) All of these.
E) None of these.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
46
A statistics professor has stated that 90% of his students pass the class. To check this claim, a random sample of 150 students who have taken the class indicated that 129 passed the class. If the professor's claim is correct, what is the probability that 129 or fewer will pass the class this semester?
A) .9484
B) .0516
C) .5516
D) .4484
E) .1624
A) .9484
B) .0516
C) .5516
D) .4484
E) .1624

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
47
Completely describe the distribution of the sample proportion for samples of size n = 500 from a population with p = 0.4.
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
48
A recent nationwide survey by the American Cancer Society found the percentage of women who smoke has increased to 30%. That seems a little low for your state, so you sample 500 women from your state and find 180 of them smoke.
Find the sample proportion of women who smoke in your state.
______________
Describe sampling distribution of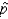 ; the proportion of women who smoke.
; the proportion of women who smoke.
Is the sampling distribution approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that at least 36% of women in your state are smokers if the true population proportion p = 0.30?
______________
Does your answer to the previous question cast doubt on the American Cancer Society's claim?
______________
Find the sample proportion of women who smoke in your state.
______________
Describe sampling distribution of
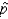 ; the proportion of women who smoke.
; the proportion of women who smoke.Is the sampling distribution approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that at least 36% of women in your state are smokers if the true population proportion p = 0.30?
______________
Does your answer to the previous question cast doubt on the American Cancer Society's claim?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose public opinion is split 65% against and 35% for increasing taxes to help balance the federal budget. 500 people from the population are selected randomly and interviewed.
Is the sampling distribution of the sample proportion of people who are in favor of increasing taxes to help balance the federal budget approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability the proportion favoring a tax increase is more than 30%?
______________
Is the sampling distribution of the sample proportion of people who are in favor of increasing taxes to help balance the federal budget approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability the proportion favoring a tax increase is more than 30%?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
50
The proportion of individuals with an Rh-positive blood type is 88%. You have a random sample of n = 500 individuals.
What is the mean of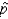 , the sample proportion with Rh-positive blood type?
, the sample proportion with Rh-positive blood type?
______________
What is the standard deviation?
______________
Is the distribution approximately normal?
______________
What is the probability that the sample proportion exceeds 85%.
______________
What is the probability that the sample proportion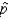 lies between 86% and 91%?
lies between 86% and 91%?
______________
99% of the time, the sample proportion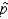 would lie between what two limits?
would lie between what two limits?
Lower Limit = ______________
Upper Limit = ______________
What is the mean of
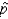 , the sample proportion with Rh-positive blood type?
, the sample proportion with Rh-positive blood type?______________
What is the standard deviation?
______________
Is the distribution approximately normal?
______________
What is the probability that the sample proportion exceeds 85%.
______________
What is the probability that the sample proportion
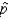 lies between 86% and 91%?
lies between 86% and 91%?______________
99% of the time, the sample proportion
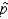 would lie between what two limits?
would lie between what two limits?Lower Limit = ______________
Upper Limit = ______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
51
Assume that the proportion of defective items in a sample of 400 items is 0.20.
Is the normal approximation to the sampling distribution of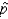 appropriate in this situation?
appropriate in this situation?
______________
Find the probability that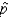 is greater than 0.23.
is greater than 0.23.
______________
Find the probability that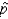 lies between 0.16 and 0.24.
lies between 0.16 and 0.24.
______________
Is the normal approximation to the sampling distribution of
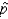 appropriate in this situation?
appropriate in this situation?______________
Find the probability that
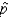 is greater than 0.23.
is greater than 0.23.______________
Find the probability that
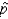 lies between 0.16 and 0.24.
lies between 0.16 and 0.24.______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
52
A well-known juice manufacturer claims that its citrus punch contains 15% real orange juice. A random sample of 150 cans of the citrus punch is selected and analyzed for content composition.
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion will be less than 0.10.
______________
Would a value of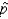 = 0.25 be considered unusual?
= 0.25 be considered unusual?
______________
Explain.
________________________________________________________
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion will be less than 0.10.
______________
Would a value of
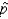 = 0.25 be considered unusual?
= 0.25 be considered unusual?______________
Explain.
________________________________________________________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
53
A TV pollster believed that 70% of all TV households would be tuned in to Game 6 of the 1997 NBA Championship series between the Chicago Bulls and the Utah Jazz. A random sample of 500 TV households is selected.
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion on will be between 0.65 and 0.75.
______________
Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample proportion on will be between 0.65 and 0.75.
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
54
Which of the following statements is false regarding the Central Limit Theorem (CLT) of the sample proportion 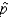 ?
?
A) CLT indicates that the mean of the sampling distribution ofwill be equal to the population proportion p.
B) CLT indicates that the sampling distribution ofcan be approximated by a normal distribution if np > 5 and nq > 5.
C) CLT is applied regardless of the sample size n and the population proportion p.
D) CLT is applied to non-normal populations.
E) CLT indicates that the mean of the sampling distribution ofwill be equal to the population proportion p and CLT indicates that the sampling distribution ofcan be approximated by a normal distribution if np > 5 and nq > 5.
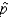 ?
?A) CLT indicates that the mean of the sampling distribution ofwill be equal to the population proportion p.
B) CLT indicates that the sampling distribution ofcan be approximated by a normal distribution if np > 5 and nq > 5.
C) CLT is applied regardless of the sample size n and the population proportion p.
D) CLT is applied to non-normal populations.
E) CLT indicates that the mean of the sampling distribution ofwill be equal to the population proportion p and CLT indicates that the sampling distribution ofcan be approximated by a normal distribution if np > 5 and nq > 5.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
55
Given a population proportion of p = .8 and a sample size of n = 100, these imply a standard deviation of the sampling distribution of the sample proportion 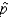 of:
of:
A) .0258
B) .0355
C) .0400
D) .0538
E) none of these
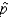 of:
of:A) .0258
B) .0355
C) .0400
D) .0538
E) none of these

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
56
Suppose a sample of 120 items is drawn from a population of manufactured products and the number of defective items is recorded. Prior experience has shown that the proportion of defectives is 0.05.
Is the sampling distribution of the proportion of defectives approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion is less than 0.10?
______________
How would the sampling distribution of the sample proportion change if the sample size were raised to 200?
________________________________________________________
Is the sampling distribution of the proportion of defectives approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion is less than 0.10?
______________
How would the sampling distribution of the sample proportion change if the sample size were raised to 200?
________________________________________________________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
57
A machine which manufactures a part for a car engine was observed over a period of time before a random sample of 300 parts was selected from those produced by this machine. Out of the 300 parts, 15 were defective.
Find the proportion of defective parts in the sample.
______________
Is the sampling distribution of the proportion of defectives approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion will lie within 0.02 of the true population proportion of defective parts?
______________
Find the proportion of defective parts in the sample.
______________
Is the sampling distribution of the proportion of defectives approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion will lie within 0.02 of the true population proportion of defective parts?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
58
In a recent study, it was reported that the proportion of employees who miss work on Fridays is 0.15, and that the standard deviation of the sampling distribution of sample proportion 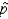 is 0.025. However, the report did not indicate what the sample size n was. What was it?
is 0.025. However, the report did not indicate what the sample size n was. What was it?
A) 204
B) 26
C) 108
D) 58
E) More information needed to determine the value of n.
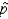 is 0.025. However, the report did not indicate what the sample size n was. What was it?
is 0.025. However, the report did not indicate what the sample size n was. What was it?A) 204
B) 26
C) 108
D) 58
E) More information needed to determine the value of n.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
59
Which of the following statement is true?
A) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same.
B) The standard deviation of the sampling distribution of the proportionis denoted by SE ().
C) The standard deviation of the sampling distribution of the proportionis denoted by().
D) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same and The standard deviation of the sampling distribution of the proportionis denoted by SE ().
E) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same and The standard deviation of the sampling distribution of the proportionis denoted by().
A) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same.
B) The standard deviation of the sampling distribution of the proportionis denoted by SE ().
C) The standard deviation of the sampling distribution of the proportionis denoted by().
D) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same and The standard deviation of the sampling distribution of the proportionis denoted by SE ().
E) The mean of all possible sample proportionsand the expected value of the sampling distribution ofare the same and The standard deviation of the sampling distribution of the proportionis denoted by().

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
60
A southern state has an unemployment rate of 6%. The state conducts monthly surveys in order to track the unemployment rate. In a recent month, a random sample of 700 people showed that 35 were unemployed.
If the true unemployment rate is 6%, describe the sampling distribution of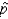 . Is the sampling distribution of the sample proportion approximately normal?
. Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample unemployment rate is at most 5%.
______________
Assume the population proportion, p, is unknown. Describe the sampling distribution of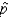 based on the most recent sample. Is the sampling distribution of the sample proportion approximately normal?
based on the most recent sample. Is the sampling distribution of the sample proportion approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
Based on the most recent sample, find the probability that the sample proportion will lie within 0.005 of the true proportion p of people who are unemployed.
______________
If the true unemployment rate is 6%, describe the sampling distribution of
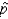 . Is the sampling distribution of the sample proportion approximately normal?
. Is the sampling distribution of the sample proportion approximately normal?______________
What is the mean?
______________
What is the standard deviation?
______________
Find the probability that the sample unemployment rate is at most 5%.
______________
Assume the population proportion, p, is unknown. Describe the sampling distribution of
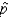 based on the most recent sample. Is the sampling distribution of the sample proportion approximately normal?
based on the most recent sample. Is the sampling distribution of the sample proportion approximately normal?______________
What is the mean?
______________
What is the standard deviation?
______________
Based on the most recent sample, find the probability that the sample proportion will lie within 0.005 of the true proportion p of people who are unemployed.
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
61
The total area under a probability density function curve is a number between 0.5 and 1.0.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
62
The sampling distribution of the sample mean is exactly normally distributed, regardless of the sample size n.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
63
The most important contribution of the Central Limit Theorem is in statistical inference.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
64
According to one study, 50% of Americans admit to overeating sweet foods when stressed. Suppose that the 50% figure is correct and that a random sample of n = 100 Americans is selected.
Does the distribution of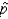 , the sample proportion of Americans who relieve stress by overeating sweet foods, have an approximately normal distribution?
, the sample proportion of Americans who relieve stress by overeating sweet foods, have an approximately normal distribution?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion,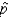 , exceeds 0.54?
, exceeds 0.54?
______________
What is the probability that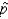 lies within the interval 0.39 to 0.59?
lies within the interval 0.39 to 0.59?
______________
Would it be unusual if the sample proportion were as small as 34%?
______________
Does the distribution of
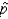 , the sample proportion of Americans who relieve stress by overeating sweet foods, have an approximately normal distribution?
, the sample proportion of Americans who relieve stress by overeating sweet foods, have an approximately normal distribution?______________
What is the mean?
______________
What is the standard deviation?
______________
What is the probability that the sample proportion,
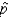 , exceeds 0.54?
, exceeds 0.54?______________
What is the probability that
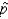 lies within the interval 0.39 to 0.59?
lies within the interval 0.39 to 0.59?______________
Would it be unusual if the sample proportion were as small as 34%?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
65
The standard deviation of a statistic that is used to estimate an unknown parameter is called the standard error of the statistic.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
66
The sample standard deviations measures the variability of all possible sample mean 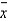 values that might be obtained.
values that might be obtained.
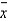 values that might be obtained.
values that might be obtained.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
67
According to the Central Limit Theorem, for large samples the standard error of the sample mean is the population standard deviation divided by the square root of the sample size.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
68
The Central Limit Theorem does not apply to the sample means of large samples drawn from a discrete distribution.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
69
The total area under a probability density function curve is equal to 1.0.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
70
If random samples of size n = 36 are drawn from a nonnormal population with finite mean  and standard deviation
and standard deviation 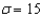 , then the sampling distribution of the sample mean
, then the sampling distribution of the sample mean 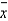 is approximately normally distributed with mean
is approximately normally distributed with mean 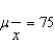 and standard deviation
and standard deviation 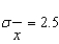
 and standard deviation
and standard deviation 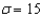 , then the sampling distribution of the sample mean
, then the sampling distribution of the sample mean 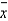 is approximately normally distributed with mean
is approximately normally distributed with mean 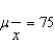 and standard deviation
and standard deviation 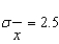

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
71
When all possible simple random samples of size n are drawn from a population that is normally distributed, the sampling distribution of the sample means 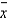 will be normal regardless of sample size n.
will be normal regardless of sample size n.
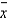 will be normal regardless of sample size n.
will be normal regardless of sample size n.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
72
The spread of the distribution of sample means is considerably less than the spread of the sampled population.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
73
As the sample size increases, the standard error of the sample mean decreases.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
74
A summary measure calculated for a population is called a parameter and is designated by Greek letters (such as 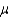 for mean or
for mean or 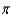 for proportion).
for proportion).
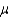 for mean or
for mean or 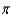 for proportion).
for proportion).
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
75
If 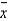 is the mean of a simple random sample taken from a large population and if the N population values are normally distributed, the sampling distribution of
is the mean of a simple random sample taken from a large population and if the N population values are normally distributed, the sampling distribution of 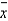 is also normally distributed, regardless of sample size, n.
is also normally distributed, regardless of sample size, n.
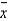 is the mean of a simple random sample taken from a large population and if the N population values are normally distributed, the sampling distribution of
is the mean of a simple random sample taken from a large population and if the N population values are normally distributed, the sampling distribution of 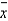 is also normally distributed, regardless of sample size, n.
is also normally distributed, regardless of sample size, n.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
76
A sampling distribution is a probability distribution that shows the likelihood of occurrence associated with all the possible values of a parameter, which values would be obtained when drawing all possible samples of a given size from a population.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
77
If random samples of size n = 50 are drawn from a nonnormal population with finite mean 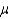 =100 and standard deviation
=100 and standard deviation 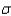 = 20, then, the sampling distribution of the sum of sample measurements
= 20, then, the sampling distribution of the sum of sample measurements 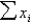 is approximately normally distributed with mean
is approximately normally distributed with mean 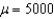 and standard deviation
and standard deviation 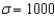 .
.
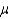 =100 and standard deviation
=100 and standard deviation 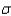 = 20, then, the sampling distribution of the sum of sample measurements
= 20, then, the sampling distribution of the sum of sample measurements 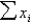 is approximately normally distributed with mean
is approximately normally distributed with mean 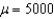 and standard deviation
and standard deviation 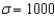 .
.
Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
78
A production process produces 10 percent defective items.
Describe the sampling distribution of the proportion of defectives for a simple random sample of n = 50.
Is the distribution approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the likelihood of encountering a sample proportion within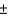 0.03 of the population proportion?
0.03 of the population proportion?
______________
If the production process is shut down whenever a sample proportion of defectives exceeds 0.05, what is the likelihood of this happening?
______________
Describe the sampling distribution of the proportion of defectives for a simple random sample of n = 50.
Is the distribution approximately normal?
______________
What is the mean?
______________
What is the standard deviation?
______________
What is the likelihood of encountering a sample proportion within
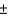 0.03 of the population proportion?
0.03 of the population proportion?______________
If the production process is shut down whenever a sample proportion of defectives exceeds 0.05, what is the likelihood of this happening?
______________

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
79
A sampling distribution is defined as a sample chosen in such a way that every possible subset of like size has an equal chance of being selected.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck
80
The Central Limit Theorem describes the distribution of the sample mean except for populations that are normal.

Unlock Deck
Unlock for access to all 162 flashcards in this deck.
Unlock Deck
k this deck


