Deck 4: Probability

Question 1

The objective of statistics is to make inferences about a population based on information contained in a sample.

Answer 1

True

Question 2

Sampling n items from a population of size N without replacements is referred to as combinations.

Answer 2

True

Question 3

An event is a process that produces outcomes.

Answer 3

False

Question 4

If two events are mutually exclusive, then the two events are also independent.

Question 5

The symbol $\cup$ represents the intersection of two events.

Question 6

All possible elementary events for an experiment is referred to as collectively exhaustive events.

Question 7

The symbol $\cup$ represents the union of two events.

Question 8

An experiment is a process that produces outcomes.

Question 9

The method of assigning probabilities to uncertain outcomes based on laws and rules is called the classical method.

Question 10

If the occurrence of one event precludes the occurrence of another event, then the two events are independent.

Question 11

A probability of an event will have a value ranging from -1 to +1.

Question 12

Assigning probabilities by dividing the number of ways that an event can occur by the total number of possible outcomes in an experiment is called the relative frequency of occurrence method.

Question 13

If the occurrence of one event does not affect the occurrence of another event, then the two events are mutually exclusive.

Question 14

The list of all elementary events for an experiment is called the sample space.

Question 15

The probability of an event A is equal to the sum of the probabilities of the sample points in A.

Question 16

An event that cannot be broken down into other events is called a certainty outcome.

Question 17

Probability is used to develop knowledge of the fundamental mathematical tools for quantitatively assessing risk.

Question 18

Assigning probabilities to uncertain events based on one's beliefs or intuitions is called classical method.

Question 19

Inferring the value of a population parameter from the statistic on a random sample drawn from the population is an inferential process under uncertainty.

Question 20

The mn counting rule may only be used when there are two operations from which to count.

Question 21

If the probability that someone likes the color blue is 44% and the probability that individuals wake up early is 64%, then the probability that individuals who like the color blue and wake up early is about 23%.In this case, the two events are independent.

Question 22

Buyers of television sets are offered a choice of one of three different styles.There are 9 different outcomes if two customers make a selection.

Question 23

Events A and B are said to be independent if either P(A $\mid$ B)= P(B)or if P(B $\mid$ A)= P(A).

Question 24

Given two events, A and B, if the probability of either A or B occurring is 0.6, then the probability of neither A nor B occurring is -0.6.

Question 25

A joint probability is the same as the intersection of two or more events.

Question 26

The law of multiplication gives the probability that at least one of the two events will occur.

Question 27

The general law of addition is P(X $\cup$ Y)= P(X)+ P(Y)- P(X $\cap$ Y).

Question 28

If P(X|Y)= P(X)then the events X and Y are independent.

Question 29

There are 4 simple events in a two-coin toss experiment.

Question 30

Given that two events, A and B, are independent, if the marginal probability of A is 0.6, the conditional probability of A given B will be 0.4.

Question 31

Given two events, A and B, if the probability of either A or B occurring is 0.8, then the probability of neither A nor B occurring is -0.8.

Question 32

The probability of A $\cup$ B where A is receiving a state grant and B is receiving a federal grant is the probability of receiving no more than one of the two grants.

Question 33

The general law of addition is P(X $\cap$ Y)= P(X)+ P(Y)- P(X $\cup$ Y).

Question 34

If the probability that someone likes the color blue is 44% and the probability that among those individuals, the probability that they wake up early is 52%, then the probability that individuals who like the color blue and wake up early is about 23%.

Question 35

The probability that a person's favorite color is blue would be an example of a marginal probability.

Question 36

Given two events, A and B, if the probability of A is 0.7, the probability of B is 0.3, and the joint probability of A and B is 0.21, then the two events are independent.

Question 37

Buyers of television sets are offered a choice of one of three different styles.There are 720 different outcomes if ten customers make a selection.

Question 38

In the conditional probability P(E₁|E₂)is interpreted as given that E₂ has occurred what is the probability of E₁ occurring.

Question 39

If two events are mutually exclusive, then their joint probability is always zero.

Question 40

A joint probability is the probability that at least one of two events occur.

Question 41

Five people are selected from a group of 20 to form a committee.How many different committee combinations could be formed?

A)100
B)120
C)15,504
D)3.2 Million
E)9,5 Billion

Question 42

Given two events A and B each with a non-zero probability, if the conditional probability of A given B is zero, it implies that the events A and B are independent.

Question 43

P(B $\mid$ A)denotes a conditional probability.

Question 44

In a set of 10 aluminum castings, two castings are defective (D), and the remaining eight are good (G).A quality control inspector randomly selects three of the ten castings with replacement and classifies each as defective (D)or good (G).How large is the sample space?

A)1,000
B)720
C)100
D)10
E)3

Question 45

Buyers of television sets are offered a choice of one of three different styles.How many different outcomes could result if two customers make a selection?

A)3
B)5
C)6
D)8
E)9

Question 46

The intersection of two events, M and N is denoted by ___.

A)(MN)
B)M $\subset$ N
C)M $\cap$ N
D)M $\cup$ N
E)M $\supset$ N

Question 47

Bayes' rule is an extension of the law of conditional probabilities to allow revision of original probabilities with new information.

Question 48

The list of all elementary events for an experiment is called ___.

A)the sample space
B)the exhaustive list
C)the population space
D)the event union
E)a frame

Question 49

Which of the following statements is not true regarding probabilities:

A)probability is the basis for inferential statistics
B)probabilities are subjective measures with limited value in business.
C)probabilities are used to determine the likelihood of certain outcomes
D)probabilities can inform many business decisions.

Question 50

Belinda Bose is reviewing a newly proposed advertising campaign.Based on her 15 years experience, she believes the campaign has a 75% chance of significantly increasing brand name recognition of the product.This is an example of assigning probabilities using the ___ method.

A)subjective probability
B)relative frequency
C)classical probability
D)a priori probability
E)a posterior probability

Question 51

In a set of 15 aluminum castings, two castings are defective (D), and the remaining thirteen are good (G).A quality control inspector randomly selects three of the fifteen castings without replacement and classifies each as defective (D)or good (G).How large is the sample space?

A)3,375
B)2,730
C)455
D)15
E)3

Question 52

P(B $\mid$ A)denotes the posterior probability of event B given event A.

Question 53

The union of two events, M and N is denoted by ___.

A)(MN)
B)M $\subset$ N
C)M $\cap$ N
D)M $\cup$ N
E)M $\supset$ N

Question 54

Buyers of television sets are offered a choice of one of three different styles.How many different outcomes could result if ten customers make a selection?

A)30
B)120
C)720
D)1000
E)59049

Question 55

Which of the following is not a legitimate probability value?

A)0.67
B)15/16
C)0.23
D)4/3
E)0.98

Question 56

Given two events A and B each with a non-zero probability, if the conditional probability of A given B is zero, it implies that the events A and B are mutually exclusive.

Question 57

Which of the following is a legitimate probability value?

A)1.67
B)16/15
C)-0.23
D)3/2
E)0.28

Question 58

Bayes' rule is a rule to assign probabilities under the classical method.

Question 59

Assigning probability 1/52 on drawing the ace of spade in a deck of cards is an example of assigning probabilities using the ________________ method

A)subjective probability
B)relative frequency
C)classical probability
D)prior probability
E)posterior probability

Question 60

P(B)denotes an unconditional probability.

Question 61

Abel Alonzo, Director of Human Resources, is exploring employee absenteeism at the Plano Power Plant.10% of all plant employees work in the finishing department; 20% of all plant employees are absent excessively; and 7% of all plant employees work in the finishing department and are absent excessively.A plant employee is selected randomly; F is the event "works in the finishing department;" and A is the event "is absent excessively." P(A $\cup$ F)= ___.

A)0.07
B)0.10
C)0.20
D)0.23
E)0.37

Question 62

The probability that given one event has occurred that another event would occur would be an example of _________ probability.

A)marginal
B)union
C)joint
D)conditional
E)non-union

Question 63

Meagan Dubean manages a portfolio of 200 common stocks.Her staff classified the portfolio stocks by 'industry sector' and 'investment objective.' 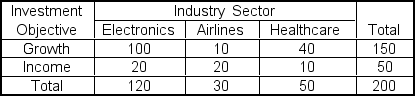Which of the following statements is NOT true?

A)Growth and Income are complementary events.
B)Electronics and Growth are dependent.
C)Electronics and Healthcare are mutually exclusive.
D)Airlines and Healthcare are collectively exhaustive.
E)Growth and Income are collectively exhaustive.

Question 64

Let A be the event that a student is enrolled in an accounting course, and let S be the event that a student is enrolled in a statistics course.It is known that 30% of all students are enrolled in an accounting course and 40% of all students are enrolled in statistics.Included in these numbers are 15% who are enrolled in both statistics and accounting.Find the probability that a student is in accounting and is also in statistics.

A)0.15
B)0.70
C)0.55
D)0.12
E)0.60

Question 65

Consider the following sample space, S, and several events defined on it.S = {Albert, Betty, Abel, Jack, Patty, Meagan}, and the events are: F = {Betty, Patty, Meagan}, H = {Abel, Meagan}, and P = {Betty, Abel}.The complement of F is ___.

A){Albert, Betty, Jack, Patty}
B){Betty, Patty, Meagan}
C){Albert, Abel, Jack}
D){Betty, Abel}
E){Meagan}

Question 66

Consider the following sample space, S, and several events defined in it.S = {Albert, Betty, Abel, Jack, Patty, Meagan}, and the events are: F = {Betty, Patty, Meagan}, H = {Abel, Meagan}, and P = {Betty, Abel}.F $\cap$ H is ___.

A){Meagan}
B){Betty, Patty, Abel, Meagan}
C)empty, since F and H are complements
D)empty, since F and H are independent
E)empty, since F and H are mutually exclusive

Question 67

If the CEO of Apple wanted to know the probability that someone would own an Apple computer and spend more than 20 hours each week on the internet would be an example of a _____________ probability.

A)unconditional
B)union
C)joint
D)marginal
E)conditional

Question 68

One event is that individuals like lasagna and the other event is that individuals like soda, the union of these two events would be the probability of _____________.

A)both events occurring
B)at least one event occurring
C)neither event occurring
D)0%
E)100%

Question 69

If X and Y are mutually exclusive events, then if X occurs, ___.

A)Y must also occur
B)Y cannot occur
C)X and Y are independent
D)X and Y are complements
E)A and Y are collectively exhaustive

Question 70

Let A be the event that a student is enrolled in an accounting course, and let S be the event that a student is enrolled in a statistics course.It is known that 30% of all students are enrolled in an accounting course and 40% of all students are enrolled in statistics.Included in these numbers are 15% who are enrolled in both statistics and accounting.A student is randomly selected, what is the probability that the student is enrolled in either accounting or statistics or both?

A)0.15
B)0.85
C)0.70
D)0.55
E)0.90

Question 71

The number of different committees of 2 students that can be chosen from a group of 5 students is

A)20
B)2
C)5
D)10
E)1

Question 72

The CEO of Apple wanted to know the probability that someone would own an Apple computer or spend more than 20 hours each week on the internet, this would be an example of a ______________ probability.

A)union
B)unconditional
C)marginal
D)conditional
E)joint

Question 73

Max Sandlin is exploring the characteristics of stock market investors.He found that 60% of all investors have a net worth exceeding $1,000,000; 20% of all investors use an online brokerage; and 10% of all investors a have net worth exceeding $1,000,000 and use an online brokerage.An investor is selected randomly, and E is the event "net worth exceeds $1,000,000" and O is the event "uses an online brokerage." P(O $\cup$ E)= ___.

A)0.17
B)0.50
C)0.80
D)0.70
E)0.10

Question 74

Let A be the event that a student is enrolled in an accounting course, and let S be the event that a student is enrolled in a statistics course.It is known that 30% of all students are enrolled in an accounting course and 40% of all students are enrolled in statistics.Included in these numbers are 15% who are enrolled in both statistics and accounting.A student is randomly selected, and it is found that the student is enrolled in accounting.What is the probability that this student is also enrolled in statistics?

A)0.15
B)0.75
C)0.375
D)0.50
E)0.80

Question 75

Let A be the event that a student is enrolled in an accounting course, and let S be the event that a student is enrolled in a statistics course.It is known that 30% of all students are enrolled in an accounting course and 40% of all students are enrolled in statistics.Included in these numbers are 15% who are enrolled in both statistics and accounting.Find P(S).

A)0.15
B)0.30
C)0.40
D)0.55
E)0.60

Question 76

If the CEO of Apple wanted to know the probability that if someone owned an Apple computer, they would also own a different brand computer, this would be an example of a __________ probability.

A)conditional
B)marginal
C)joint
D)non-joint
E)union

Question 77

If X and Y are mutually exclusive, then ___.

A)the probability of the union is zero
B)P(X)= 1 - P(Y)
C)the probability of the intersection is zero
D)the probability of the union is one
E)P(Y)= P(X)

Question 78

The probability of at least one of two events occurring would be an example of a____________ probability.

A)marginal
B)union
C)joint
D)conditional
E)non-union

Question 79

Consider the following sample space, S, and several events defined in it.S = {Albert, Betty, Abel, Jack, Patty, Meagan}, and the events are: F = {Betty, Patty, Meagan}, H = {Abel, Meagan}, and P = {Betty, Abel}.F $\cup$ H is ___.

A){Meagan}
B){Betty, Abel, Patty, Meagan}
C)empty, since F and H are complements
D)empty, since F and H are independent
E)empty, since F and H are mutually exclusive

Question 80

Meagan Dubean manages a portfolio of 200 common stocks.Her staff classified the portfolio stocks by 'industry sector' and 'investment objective.' 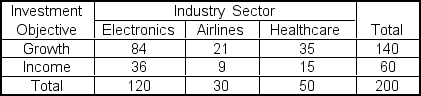Which of the following statements is true?

A)Growth and Healthcare are complementary events.
B)Electronics and Growth are independent.
C)Electronics and Growth are mutually exclusive.
D)Airlines and Healthcare are collectively exhaustive.
E)Electronics and Healthcare are collectively exhaustive.