Deck 20: Inventory Management: Economic Order Quantity, Jit, and the Theory of Constraints
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/41
Play
Full screen (f)
Deck 20: Inventory Management: Economic Order Quantity, Jit, and the Theory of Constraints
1
Explain why, in the traditional view of inventory, carrying costs increase as ordering costs decrease.
In the traditional view of inventory, carrying cost is inversely proportional to the ordering cost. It is because as the order quantity increases, ordering cost may get reduced but the carrying cost increases. Increase in the order quantity reduces the total number of annual orders and hence the ordering cost may get reduced. But as the ordering quantity increases, handling cost and other cost related to carrying cost increases with the number of units. Thus, the carrying costs increases as the ordering costs decreases.
2
EOQ WITH SETUP COSTS
Cushing Manufacturing produces casings for sewing machines: large and small. To produce the different casings, equipment must be set up. The setup cost per production run is $9,000 for either casing. The cost of carrying small casings in inventory is $3 per casing per year; the cost of large casings is $9 per unit per year. To satisfy demand, the company produces 600,000 small casings and 200,000 large casings.
Required:
1. Compute the number of small casings that should be produced per setup to minimize total setup and carrying costs.
2. Compute the setup, carrying, and total costs associated with the economic order quantity for the small casings.
Cushing Manufacturing produces casings for sewing machines: large and small. To produce the different casings, equipment must be set up. The setup cost per production run is $9,000 for either casing. The cost of carrying small casings in inventory is $3 per casing per year; the cost of large casings is $9 per unit per year. To satisfy demand, the company produces 600,000 small casings and 200,000 large casings.
Required:
1. Compute the number of small casings that should be produced per setup to minimize total setup and carrying costs.
2. Compute the setup, carrying, and total costs associated with the economic order quantity for the small casings.
We are given the following costs of casings for C Manufacturing:
Annual Demand, D (Small casings) = 600,000; D (Large casings) = 200,000
Setup Cost, S = $9,000
Carrying cost, C (Small casings) = $3; C (Large casings) = $9
We are required to compute the number of small casings that should be produced per setup to minimize total setup and carrying costs.
1. Number of casings are computed as under:
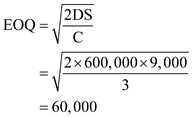 2. Setup cost is computed as under:
2. Setup cost is computed as under:
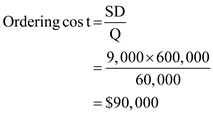 Carrying cost is computed as under:
Carrying cost is computed as under:
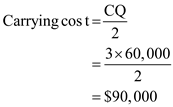
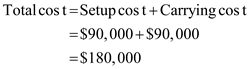
Annual Demand, D (Small casings) = 600,000; D (Large casings) = 200,000
Setup Cost, S = $9,000
Carrying cost, C (Small casings) = $3; C (Large casings) = $9
We are required to compute the number of small casings that should be produced per setup to minimize total setup and carrying costs.
1. Number of casings are computed as under:
 2. Setup cost is computed as under:
2. Setup cost is computed as under: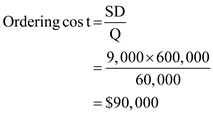 Carrying cost is computed as under:
Carrying cost is computed as under: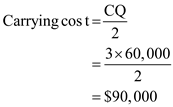
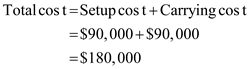
3
Product Mix Decision, Single and Multiple Constraints, Basics of Linear Programming
Desayuno Products, Inc., produces cornflakes and branflakes. The manufacturing process is highly mechanized; both products are produced by the same machinery by using different settings. For the coming period, 200,000 machine hours are available. Management is trying to decide on the quantities of each product to produce. The following data are available:
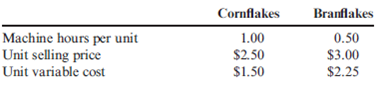
Required:
1. Determine the units of each product that should be produced in order to maximize profits.
2. Because of market conditions, the company can sell no more than 150,000 boxes of cornflakes and 300,000 boxes of branflakes. Do the following:
a. Formulate the problem as a linear programming problem.
b. Determine the optimal mix using a graph.
c. Compute the maximum contribution margin given the optimal mix.
Desayuno Products, Inc., produces cornflakes and branflakes. The manufacturing process is highly mechanized; both products are produced by the same machinery by using different settings. For the coming period, 200,000 machine hours are available. Management is trying to decide on the quantities of each product to produce. The following data are available:
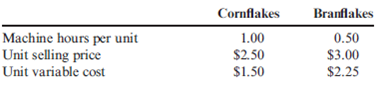
Required:
1. Determine the units of each product that should be produced in order to maximize profits.
2. Because of market conditions, the company can sell no more than 150,000 boxes of cornflakes and 300,000 boxes of branflakes. Do the following:
a. Formulate the problem as a linear programming problem.
b. Determine the optimal mix using a graph.
c. Compute the maximum contribution margin given the optimal mix.
We are given the data relating to cornflakes and branflakes being produced by D P Inc. We are required to determine the optimal mix given the different scenarios.
1. The optimal mix is computed as follows:
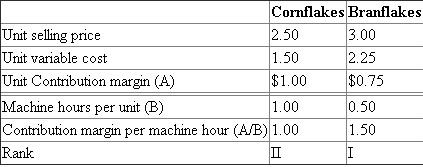 Ranking indicates that all the machine hours should be allocated to the production of branflakes. The contribution margin from production of brabflakes is computed as follows:
Ranking indicates that all the machine hours should be allocated to the production of branflakes. The contribution margin from production of brabflakes is computed as follows:
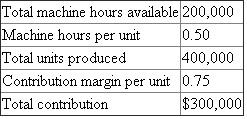 Hence, 400,000 units of branflakes should be produced to maximize the profits.
Hence, 400,000 units of branflakes should be produced to maximize the profits.
2. a. Let x units of cornflakes and y units of branflakes are produced.
Objective function:
Maximize,
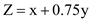 Subject to
Subject to
Internal constraint:
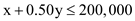 External constraints:
External constraints:
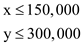 Non negativity constraints:
Non negativity constraints:
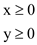 b. Graph for the above linear programming problem is prepared as follows:
b. Graph for the above linear programming problem is prepared as follows:
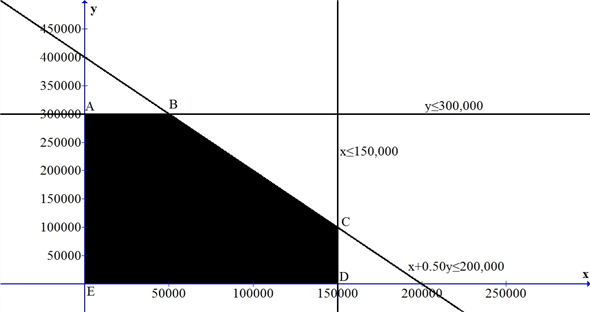 c. The coordinates of A, B, C, D and E are obtained by solving the simultaneous equations of the associated intersecting constraints within the feasible set (Region ABCDE, including the frontier).
c. The coordinates of A, B, C, D and E are obtained by solving the simultaneous equations of the associated intersecting constraints within the feasible set (Region ABCDE, including the frontier).
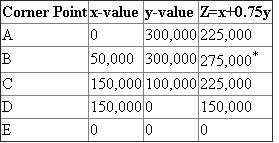 * Optimal solution.
* Optimal solution.
Hence, 50,000 units of cornflakes and 300,000 units of branflakes should be produced to maximize the contribution margin to $275,000.
1. The optimal mix is computed as follows:
 Ranking indicates that all the machine hours should be allocated to the production of branflakes. The contribution margin from production of brabflakes is computed as follows:
Ranking indicates that all the machine hours should be allocated to the production of branflakes. The contribution margin from production of brabflakes is computed as follows: Hence, 400,000 units of branflakes should be produced to maximize the profits.
Hence, 400,000 units of branflakes should be produced to maximize the profits.2. a. Let x units of cornflakes and y units of branflakes are produced.
Objective function:
Maximize,
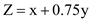 Subject to
Subject toInternal constraint:
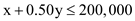 External constraints:
External constraints: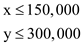 Non negativity constraints:
Non negativity constraints: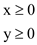 b. Graph for the above linear programming problem is prepared as follows:
b. Graph for the above linear programming problem is prepared as follows: c. The coordinates of A, B, C, D and E are obtained by solving the simultaneous equations of the associated intersecting constraints within the feasible set (Region ABCDE, including the frontier).
c. The coordinates of A, B, C, D and E are obtained by solving the simultaneous equations of the associated intersecting constraints within the feasible set (Region ABCDE, including the frontier). * Optimal solution.
* Optimal solution.Hence, 50,000 units of cornflakes and 300,000 units of branflakes should be produced to maximize the contribution margin to $275,000.
4
CONSTRAINED OPTIMIZATION: ONE INTERNAL BINDING CONSTRAINT
Fisher Company produces two types of airplane components: Component A and Component B, with unit contribution margins of $200 and $400, respectively. Assume initially that Fisher can sell all that is produced of either component. Component A requires two hours of assembly, and B requires five hours of assembly. The firm has 200 assembly hours per week.
Required:
1. Express the objective of maximizing total contribution margin subject to the assembly-hour constraint.
2. Identify the optimal amount that should be produced of each airplane component and the total contribution margin associated with this mix.
3. What if market conditions are such that Fisher can sell at most 50 units of Component A and 40 units of Component B? Express the objective function with its associated constraints for this case and identify the optimal mix and its associated total contribution margin.
Fisher Company produces two types of airplane components: Component A and Component B, with unit contribution margins of $200 and $400, respectively. Assume initially that Fisher can sell all that is produced of either component. Component A requires two hours of assembly, and B requires five hours of assembly. The firm has 200 assembly hours per week.
Required:
1. Express the objective of maximizing total contribution margin subject to the assembly-hour constraint.
2. Identify the optimal amount that should be produced of each airplane component and the total contribution margin associated with this mix.
3. What if market conditions are such that Fisher can sell at most 50 units of Component A and 40 units of Component B? Express the objective function with its associated constraints for this case and identify the optimal mix and its associated total contribution margin.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
5
What is a constraint? An internal constraint? An external constraint?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
6
Product Mix Decisions
Calen Company manufactures and sells three products in a factory of three departments. Both labor and machine time are applied to the products as they pass through each department. The nature of the machine processing and of the labor skills required in each department is such that neither machines nor labor can be switched from one department to another.
Calen's management is attempting to plan its production schedule for the next several months. The planning is complicated by the fact that labor shortages exist in the community and some machines will be down several months for repairs.
Following is information regarding available machine and labor time by department and the machine hours and direct labor hours required per unit of product. These data should be valid for at least the next six months.
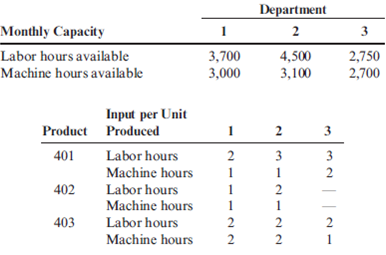
Calen believes that the monthly demand for the next six months will be as follows:
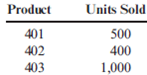
Inventory levels will not be increased or decreased during the next six months. The unit cost and price data for each product are as follows:
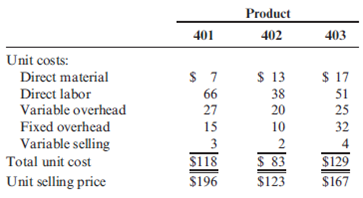
Required:
1. Calculate the monthly requirement for machine hours and direct labor hours for producing Products 401, 402, and 403 to determine whether or not the factory can meet the monthly sales demand.
2. Determine the quantities of 401, 402, and 403 that should be produced monthly to maximize profits. Prepare a schedule that shows the contribution to profits of your product mix.
3. Assume that the machine hours available in Department 3 are 1,500 instead of 2,700. Calculate the optimal monthly product mix using the graphing approach to linear programming. Prepare a schedule that shows the contribution to profits from this optimal mix. (CMA
Calen Company manufactures and sells three products in a factory of three departments. Both labor and machine time are applied to the products as they pass through each department. The nature of the machine processing and of the labor skills required in each department is such that neither machines nor labor can be switched from one department to another.
Calen's management is attempting to plan its production schedule for the next several months. The planning is complicated by the fact that labor shortages exist in the community and some machines will be down several months for repairs.
Following is information regarding available machine and labor time by department and the machine hours and direct labor hours required per unit of product. These data should be valid for at least the next six months.

Calen believes that the monthly demand for the next six months will be as follows:

Inventory levels will not be increased or decreased during the next six months. The unit cost and price data for each product are as follows:

Required:
1. Calculate the monthly requirement for machine hours and direct labor hours for producing Products 401, 402, and 403 to determine whether or not the factory can meet the monthly sales demand.
2. Determine the quantities of 401, 402, and 403 that should be produced monthly to maximize profits. Prepare a schedule that shows the contribution to profits of your product mix.
3. Assume that the machine hours available in Department 3 are 1,500 instead of 2,700. Calculate the optimal monthly product mix using the graphing approach to linear programming. Prepare a schedule that shows the contribution to profits from this optimal mix. (CMA

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
7
Discuss the traditional reasons for carrying inventory.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
8
EOQ WITH SETUP COSTS
Refer to Exercise 20-10.
Required:
1. Compute the number of large casings that should be produced per setup to minimize total setup and carrying costs for this product.
2. Compute the setup, carrying, and total costs associated with the economic order quantity for the large casings.
Refer to Exercise 20-10.
Required:
1. Compute the number of large casings that should be produced per setup to minimize total setup and carrying costs for this product.
2. Compute the setup, carrying, and total costs associated with the economic order quantity for the large casings.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
9
IDENTIFYING AND EXPLOITING CONSTRAINTS, CONSTRAINT ELEVATION
Berry Company produces two different metal components used in medical equipment (Component X and Component Y). The company has three processes: molding, grinding, and finishing. In molding, molds are created, and molten metal is poured into the shell. Grinding removes the gates that allowed the molten metal to flow into the mold's cavities. In finishing, rough edges caused by the grinders are removed by small, handheld pneumatic tools. In molding, the setup time is one hour. The other two processes have no setup time required. The demand for Component X is 300 units per day, and the demand for Component Y is 500 units per day. The minutes required per unit for each product are as follows:

The company operates one eight-hour shift. The molding process employs 12 workers (who each work eight hours). Two hours of their time, however, are used for setups (assuming both products are produced). The grinding process has sufficient equipment and workers to provide 200 grinding hours per shift.
The Finishing Department is labor intensive and employs 35 workers, who each work eight hours per day. The only significant unit-level variable costs are materials and power. For Component X, the variable cost per unit is $40, and for Component Y, it is $50. Selling prices for X and Y are $90 and $110, respectively. Berry's policy is to use two setups per day: an initial setup to produce all that is scheduled for Component X and a second setup (changeover) to produce all that is scheduled for Component Y. The amount scheduled does not necessarily correspond to each product's daily demand.
Required:
1. Calculate the time (in minutes) needed each day to meet the daily market demand for Component X and Component Y. What is the major internal constraint facing Berry Company?
2. Describe how Berry should exploit its major binding constraint. Specifically, identify the product mix that will maximize daily throughput.
3. Assume that manufacturing engineering has found a way to reduce the molding setup time from one hour to 10 minutes. Explain how this affects the product mix and daily throughput.
Berry Company produces two different metal components used in medical equipment (Component X and Component Y). The company has three processes: molding, grinding, and finishing. In molding, molds are created, and molten metal is poured into the shell. Grinding removes the gates that allowed the molten metal to flow into the mold's cavities. In finishing, rough edges caused by the grinders are removed by small, handheld pneumatic tools. In molding, the setup time is one hour. The other two processes have no setup time required. The demand for Component X is 300 units per day, and the demand for Component Y is 500 units per day. The minutes required per unit for each product are as follows:

The company operates one eight-hour shift. The molding process employs 12 workers (who each work eight hours). Two hours of their time, however, are used for setups (assuming both products are produced). The grinding process has sufficient equipment and workers to provide 200 grinding hours per shift.
The Finishing Department is labor intensive and employs 35 workers, who each work eight hours per day. The only significant unit-level variable costs are materials and power. For Component X, the variable cost per unit is $40, and for Component Y, it is $50. Selling prices for X and Y are $90 and $110, respectively. Berry's policy is to use two setups per day: an initial setup to produce all that is scheduled for Component X and a second setup (changeover) to produce all that is scheduled for Component Y. The amount scheduled does not necessarily correspond to each product's daily demand.
Required:
1. Calculate the time (in minutes) needed each day to meet the daily market demand for Component X and Component Y. What is the major internal constraint facing Berry Company?
2. Describe how Berry should exploit its major binding constraint. Specifically, identify the product mix that will maximize daily throughput.
3. Assume that manufacturing engineering has found a way to reduce the molding setup time from one hour to 10 minutes. Explain how this affects the product mix and daily throughput.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
10
CONSTRAINED OPTIMIZATION: MULTIPLE INTERNAL CONSTRAINTS
Fisher Company produces two types of components for airplanes: A and B, with unit contribution margins of $200 and $400, respectively. The components pass through three sequential processes: cutting, welding, and assembly. Data pertaining to these processes and market demand are given on the following page (weekly data).

Required:
1. Express Fisher Company's constrained optimization problem as a linear programming model.
2. Using a graphical approach, solve the linear programming model expressed in Requirement 1. Which constraints are binding?
3. What if Fisher Company had five additional machine hours (cutting) with all other resources held constant? What is the new optimal mix and associated total contribution margin? What is the incremental benefit per machine hour caused by the additional five hours, if any?
Fisher Company produces two types of components for airplanes: A and B, with unit contribution margins of $200 and $400, respectively. The components pass through three sequential processes: cutting, welding, and assembly. Data pertaining to these processes and market demand are given on the following page (weekly data).

Required:
1. Express Fisher Company's constrained optimization problem as a linear programming model.
2. Using a graphical approach, solve the linear programming model expressed in Requirement 1. Which constraints are binding?
3. What if Fisher Company had five additional machine hours (cutting) with all other resources held constant? What is the new optimal mix and associated total contribution margin? What is the incremental benefit per machine hour caused by the additional five hours, if any?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
11
Explain the procedures for graphically solving a linear programming problem. What solution method is used when the problem includes more than two or three products?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
12
Theory of Constraints, Internal Constraints
Pratt Company produces two replacement parts for a popular line of Blu-ray disc players: Part A and Part B. Part A is made up of two components, one manufactured internally and one purchased from external suppliers. Part B is made up of three components, one manufactured internally and two purchased from suppliers. The company has two processes: fabrication and assembly. In fabrication, the internally produced components are made. Each component takes 20 minutes to produce. In assembly, it takes 30 minutes to assemble the components for Part A and 40 minutes to assemble the components for Part B. Pratt Company operates one shift per day. Each process employs 100 workers who each work eight hours per day.
Part A earns a unit contribution margin of $20, and Part B earns a unit contribution margin of $24 (calculated as the difference between revenue and the cost of materials and energy). Pratt can sell all that it produces of either part. There are no other constraints. Pratt can add a second shift of either process. Although a second shift would work eight hours, there is no mandate that it employ the same number of workers. The labor cost per hour for fabrication is $15, and the labor cost per hour for assembly is $12.
Required:
1. Identify the constraints facing Pratt, and graph them. How many binding constraints are possible? What is Pratt's optimal product mix? What daily contribution margin is produced by this mix?
2. What is the drummer constraint? How much excess capacity does the other constraint have? Assume that a 1.5-day buffer inventory is needed to deal with any production interruptions. Describe the drum-buffer-rope concept using the Pratt data to illustrate the process.
3. Explain why the use of local labor efficiency measures will not work in Pratt's TOC environment.
4. Suppose Pratt decides to elevate the binding constraint by adding a second shift of 50 workers (labor rates are the same as those of the first shift). Would elevation of Pratt's binding constraint improve its system performance? Explain with supporting computations.
Pratt Company produces two replacement parts for a popular line of Blu-ray disc players: Part A and Part B. Part A is made up of two components, one manufactured internally and one purchased from external suppliers. Part B is made up of three components, one manufactured internally and two purchased from suppliers. The company has two processes: fabrication and assembly. In fabrication, the internally produced components are made. Each component takes 20 minutes to produce. In assembly, it takes 30 minutes to assemble the components for Part A and 40 minutes to assemble the components for Part B. Pratt Company operates one shift per day. Each process employs 100 workers who each work eight hours per day.
Part A earns a unit contribution margin of $20, and Part B earns a unit contribution margin of $24 (calculated as the difference between revenue and the cost of materials and energy). Pratt can sell all that it produces of either part. There are no other constraints. Pratt can add a second shift of either process. Although a second shift would work eight hours, there is no mandate that it employ the same number of workers. The labor cost per hour for fabrication is $15, and the labor cost per hour for assembly is $12.
Required:
1. Identify the constraints facing Pratt, and graph them. How many binding constraints are possible? What is Pratt's optimal product mix? What daily contribution margin is produced by this mix?
2. What is the drummer constraint? How much excess capacity does the other constraint have? Assume that a 1.5-day buffer inventory is needed to deal with any production interruptions. Describe the drum-buffer-rope concept using the Pratt data to illustrate the process.
3. Explain why the use of local labor efficiency measures will not work in Pratt's TOC environment.
4. Suppose Pratt decides to elevate the binding constraint by adding a second shift of 50 workers (labor rates are the same as those of the first shift). Would elevation of Pratt's binding constraint improve its system performance? Explain with supporting computations.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
13
What are stock-out costs?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
14
REORDER POINT
Refer to Exercise 20-10. Assume the economic lot size for small casings is 60,000 and that of the large casings is 20,000. Cushing Manufacturing sells an average of 2,400 small casings per workday and an average of 800 large casings per workday. It takes Cushing two days to set up the equipment for small or large casings. Once set up, it takes nine workdays to produce a batch of small casings and 10 days for large casings. There are 250 workdays available per year.
Required:
1. What is the reorder point for small casings? Large casings?
2. Using the economic order batch size, is it possible for Cushing to produce the amount that can be sold of each casing? Does scheduling have a role here? Explain. Is this a push or pull-through system approach to inventory management? Explain.
Refer to Exercise 20-10. Assume the economic lot size for small casings is 60,000 and that of the large casings is 20,000. Cushing Manufacturing sells an average of 2,400 small casings per workday and an average of 800 large casings per workday. It takes Cushing two days to set up the equipment for small or large casings. Once set up, it takes nine workdays to produce a batch of small casings and 10 days for large casings. There are 250 workdays available per year.
Required:
1. What is the reorder point for small casings? Large casings?
2. Using the economic order batch size, is it possible for Cushing to produce the amount that can be sold of each casing? Does scheduling have a role here? Explain. Is this a push or pull-through system approach to inventory management? Explain.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
15
TOC, Internal and External Constraints
Bountiful Manufacturing produces two types of bike frames (Frame X and Frame Y). Frame X passes through four processes: cutting, welding, polishing, and painting. Frame Y uses three of the same processes: cutting, welding, and painting. Each of the four processes employs 10 workers who work eight hours each day. Frame X sells for $40 per unit, and Frame Y sells for $55 per unit. Materials is the only unit-level variable expense. The materials cost for Frame X is $20 per unit, and the materials cost for Frame Y is $25 per unit. Bountiful's accounting system has provided the following additional information about its operations and products:

Bountiful's management has determined that any production interruptions can be corrected within two days.
Required:
1. Assuming that Bountiful can meet daily market demand, compute the potential daily profit. Now, compute the minutes needed for each process to meet the daily market demand. Can Bountiful meet daily market demand? If not, where is the bottleneck? Can you derive an optimal mix without using a graphical solution? If so, explain how.
2. Identify the objective function and the constraints. Then, graph the constraints facing Bountiful. Determine the optimal mix and the maximum daily contribution margin (throughput).
3. Explain how a drum-buffer-rope system would work for Bountiful.
4. Suppose that the Engineering Department has proposed a process design change that will increase the polishing time for Frame X from 15 to 23 minutes per unit and decrease the welding time from 15 minutes to 10 minutes per unit (for Frame X). The cost of process redesign would be $10,000. Evaluate this proposed change. What step in the TOC process does this proposal represent?
Bountiful Manufacturing produces two types of bike frames (Frame X and Frame Y). Frame X passes through four processes: cutting, welding, polishing, and painting. Frame Y uses three of the same processes: cutting, welding, and painting. Each of the four processes employs 10 workers who work eight hours each day. Frame X sells for $40 per unit, and Frame Y sells for $55 per unit. Materials is the only unit-level variable expense. The materials cost for Frame X is $20 per unit, and the materials cost for Frame Y is $25 per unit. Bountiful's accounting system has provided the following additional information about its operations and products:

Bountiful's management has determined that any production interruptions can be corrected within two days.
Required:
1. Assuming that Bountiful can meet daily market demand, compute the potential daily profit. Now, compute the minutes needed for each process to meet the daily market demand. Can Bountiful meet daily market demand? If not, where is the bottleneck? Can you derive an optimal mix without using a graphical solution? If so, explain how.
2. Identify the objective function and the constraints. Then, graph the constraints facing Bountiful. Determine the optimal mix and the maximum daily contribution margin (throughput).
3. Explain how a drum-buffer-rope system would work for Bountiful.
4. Suppose that the Engineering Department has proposed a process design change that will increase the polishing time for Frame X from 15 to 23 minutes per unit and decrease the welding time from 15 minutes to 10 minutes per unit (for Frame X). The cost of process redesign would be $10,000. Evaluate this proposed change. What step in the TOC process does this proposal represent?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
16
DRUM-BUFFER-ROPE
See Cornerstone Exercise 20-4. Fisher Company has three sequential processes: cutting, welding, and assembly. Assume that the optimal mix is: Component A = 0 units per week; Component B = 30 units per week. Demand is uniformly spread out over the five-day work week. Fisher requires a 2.5-day buffer.
Required:
1. Identify the drummer, the rate of production, the time buffer, and the rope.
2. Illustrate the DBR structure of Fisher Company.
3. What if the Welding Department was allowed or encouraged to produce at capacity? What effect will this have on work-in-process inventories?
See Cornerstone Exercise 20-4. Fisher Company has three sequential processes: cutting, welding, and assembly. Assume that the optimal mix is: Component A = 0 units per week; Component B = 30 units per week. Demand is uniformly spread out over the five-day work week. Fisher requires a 2.5-day buffer.
Required:
1. Identify the drummer, the rate of production, the time buffer, and the rope.
2. Illustrate the DBR structure of Fisher Company.
3. What if the Welding Department was allowed or encouraged to produce at capacity? What effect will this have on work-in-process inventories?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
17
Define and discuss the three measures of organizational performance used by the theory of constraints.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
18
Please answer each of the following:
Required:
1. Go to http://www.goldratt.com , and locate the list of cases detailing successful use of the theory of constraints. Pick three cases, and summarize the benefits each firm realized from implementing TOC.
2. Access the library at http://www.goldratt.com , and see if you can find any information on what TOC followers call the "Thinking Process." If not, then do a general Internet search to find the information. Once located, describe what is meant by the "Thinking Process."


Required:
1. Go to http://www.goldratt.com , and locate the list of cases detailing successful use of the theory of constraints. Pick three cases, and summarize the benefits each firm realized from implementing TOC.
2. Access the library at http://www.goldratt.com , and see if you can find any information on what TOC followers call the "Thinking Process." If not, then do a general Internet search to find the information. Once located, describe what is meant by the "Thinking Process."



Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
19
Explain how safety stock is used to deal with demand uncertainty.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
20
Safety Stock
Eyring Manufacturing produces a component used in its production of washing machines. The time to set up and produce a batch of the components is two days. The average daily usage is 800 components, and the maximum daily usage is 875 components.
Required:
Compute the reorder point assuming that safety stock is carried by Eyring Manufacturing. How much safety stock is carried by Eyring?
Eyring Manufacturing produces a component used in its production of washing machines. The time to set up and produce a batch of the components is two days. The average daily usage is 800 components, and the maximum daily usage is 875 components.
Required:
Compute the reorder point assuming that safety stock is carried by Eyring Manufacturing. How much safety stock is carried by Eyring?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
21
What is the economic order quantity?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
22
Explain how lowering inventory produces better products, lower prices, and better responsiveness to customer needs.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
23
ORDERING AND CARRYING COSTS
Larsen, Inc., uses 160,000 plastic housing units each year in its production of paper shredders. The cost of placing an order is $60. The cost of holding one unit of inventory for one year is $7.50. Currently, Larsen places 40 orders of 4,000 plastic housing units per year.
Required:
1. Compute the annual ordering cost.
2. Compute the annual carrying cost.
3. Compute the cost of Larsen's current inventory policy. Is this the minimum cost? Why or why not?
Larsen, Inc., uses 160,000 plastic housing units each year in its production of paper shredders. The cost of placing an order is $60. The cost of holding one unit of inventory for one year is $7.50. Currently, Larsen places 40 orders of 4,000 plastic housing units per year.
Required:
1. Compute the annual ordering cost.
2. Compute the annual carrying cost.
3. Compute the cost of Larsen's current inventory policy. Is this the minimum cost? Why or why not?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
24
Kanban System, EDI
Hales Company produces a product that requires two processes. In the first process, a subassembly is produced (subassembly A). In the second process, this subassembly and a subassembly purchased from outside the company (subassembly B) are assembled to produce the final product. For simplicity, assume that the assembly of one final unit takes the same time as the production of subassembly A. Subassembly A is placed in a container and sent to an area called the subassembly stores (SB stores) area. A production Kanban is attached to this container. A second container, also with one subassembly, is located near the assembly line (called the withdrawal store). This container has attached to it a withdrawal Kanban.
Required:
1. Explain how withdrawal and production Kanban cards are used to control the work flow between the two processes. How does this approach minimize inventories?
2. Explain how vendor Kanban cards can be used to control the flow of the purchased subassembly. What implications does this have for supplier relationships? What role, if any, do continuous replenishment and EDI play in this process?
Hales Company produces a product that requires two processes. In the first process, a subassembly is produced (subassembly A). In the second process, this subassembly and a subassembly purchased from outside the company (subassembly B) are assembled to produce the final product. For simplicity, assume that the assembly of one final unit takes the same time as the production of subassembly A. Subassembly A is placed in a container and sent to an area called the subassembly stores (SB stores) area. A production Kanban is attached to this container. A second container, also with one subassembly, is located near the assembly line (called the withdrawal store). This container has attached to it a withdrawal Kanban.
Required:
1. Explain how withdrawal and production Kanban cards are used to control the work flow between the two processes. How does this approach minimize inventories?
2. Explain how vendor Kanban cards can be used to control the flow of the purchased subassembly. What implications does this have for supplier relationships? What role, if any, do continuous replenishment and EDI play in this process?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
25
What approach does JIT take to minimize total inventory costs?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
26
What are the five steps that TOC uses to improve organizational performance?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
27
ECONOMIC ORDER QUANTITY
Refer to the data in Exercise 20-6.
Required:
1. Compute the economic order quantity.
2. Compute the ordering, carrying, and total costs for the EOQ.
3. How much money does using the EOQ policy save the company over the policy of purchasing 10,000 plastic housing units per order?
Refer to the data in Exercise 20-6.
Required:
1. Compute the economic order quantity.
2. Compute the ordering, carrying, and total costs for the EOQ.
3. How much money does using the EOQ policy save the company over the policy of purchasing 10,000 plastic housing units per order?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
28
JIT Limitations
Many companies have viewed JIT as a panacea-a knight in shining armor that promises rescue from sluggish profits, poor quality, and productive inefficiency. It is often lauded for its beneficial effects on employee morale and self-esteem. Yet, JIT may also cause a company to struggle and may produce a good deal of frustration. In some cases, JIT appears to deliver less than its reputation seems to call for.
Required:
Discuss some of the limitations and problems that companies may encounter when implementing a JIT system.
Many companies have viewed JIT as a panacea-a knight in shining armor that promises rescue from sluggish profits, poor quality, and productive inefficiency. It is often lauded for its beneficial effects on employee morale and self-esteem. Yet, JIT may also cause a company to struggle and may produce a good deal of frustration. In some cases, JIT appears to deliver less than its reputation seems to call for.
Required:
Discuss some of the limitations and problems that companies may encounter when implementing a JIT system.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
29
One reason for inventory is to prevent shutdowns. How does the JIT approach to inventory management deal with this potential problem?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
30
Product Mix Decision, Single Constraint
Behar Company makes three types of stainless steel frying pans. Each of the three types of pans requires the use of a special machine that has total operating capacity of 182,000 hours per year. Information on each of the three products is as follows:
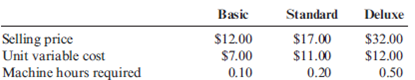
The marketing manager has determined that the company can sell all that it can produce of each of the three products.
Required:
1. How many of each product should be sold to maximize the total contribution margin? What is the total contribution margin for this product mix?
2. Suppose that Behar can sell no more than 300,000 units of each type at the prices indicated. What product mix would you recommend, and what would be the total contribution margin?
Behar Company makes three types of stainless steel frying pans. Each of the three types of pans requires the use of a special machine that has total operating capacity of 182,000 hours per year. Information on each of the three products is as follows:
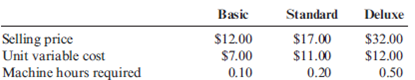
The marketing manager has determined that the company can sell all that it can produce of each of the three products.
Required:
1. How many of each product should be sold to maximize the total contribution margin? What is the total contribution margin for this product mix?
2. Suppose that Behar can sell no more than 300,000 units of each type at the prices indicated. What product mix would you recommend, and what would be the total contribution margin?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
31
Economic Order Quantity
Melchar Company uses 78,125 pounds of oats each year. The cost of placing an order is $18, and the carrying cost for one pound of oats is $0.45.
Required:
1. Compute the economic order quantity for oats.
2. Compute the carrying and ordering costs for the EOQ.
Melchar Company uses 78,125 pounds of oats each year. The cost of placing an order is $18, and the carrying cost for one pound of oats is $0.45.
Required:
1. Compute the economic order quantity for oats.
2. Compute the carrying and ordering costs for the EOQ.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
32
Drum-Buffer-Rope System
Duckstein, Inc., manufactures two types of aspirin: plain and buffered. It sells all it produces. Recently, Duckstein implemented a TOC approach for its Fort Smith plant. One binding constraint was identified, and the optimal product mix was determined. The following diagram reflects the TOC outcome:
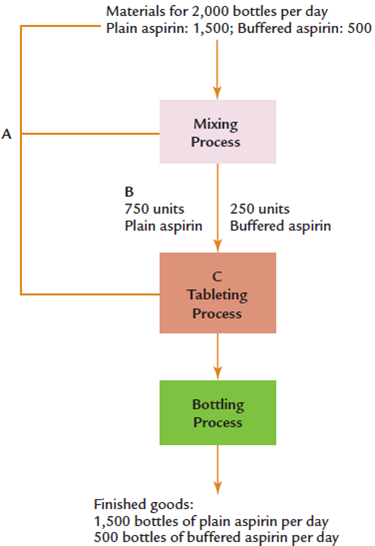
Required:
1. What is the daily production rate? Which process sets this rate?
2. How many days of buffer inventory is Duckstein carrying? How is this time buffer determined?
3. Explain what the letters A, B, and C in the exhibit represent. Discuss each of their roles in the TOC system.
Duckstein, Inc., manufactures two types of aspirin: plain and buffered. It sells all it produces. Recently, Duckstein implemented a TOC approach for its Fort Smith plant. One binding constraint was identified, and the optimal product mix was determined. The following diagram reflects the TOC outcome:

Required:
1. What is the daily production rate? Which process sets this rate?
2. How many days of buffer inventory is Duckstein carrying? How is this time buffer determined?
3. Explain what the letters A, B, and C in the exhibit represent. Discuss each of their roles in the TOC system.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
33
EOQ
Sterling Corporation produces air conditioning units. The following values apply for a part used in their production (purchased from external suppliers):
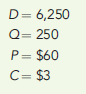
Required:
1. For Sterling, calculate the ordering cost, the carrying cost, and the total cost associated with an order size of 250 units.
2. Calculate the EOQ and its associated ordering cost, carrying cost, and total cost. Compare and comment on the EOQ relative to the current order quantity.
3. What if Sterling enters into an exclusive supplier agreement with one supplier who will supply all of the demands with smaller, more frequent orders? Under this arrangement, the ordering cost is reduced to $0.60 per order. Calculate the new EOQ and comment on the implications.
Sterling Corporation produces air conditioning units. The following values apply for a part used in their production (purchased from external suppliers):
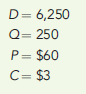
Required:
1. For Sterling, calculate the ordering cost, the carrying cost, and the total cost associated with an order size of 250 units.
2. Calculate the EOQ and its associated ordering cost, carrying cost, and total cost. Compare and comment on the EOQ relative to the current order quantity.
3. What if Sterling enters into an exclusive supplier agreement with one supplier who will supply all of the demands with smaller, more frequent orders? Under this arrangement, the ordering cost is reduced to $0.60 per order. Calculate the new EOQ and comment on the implications.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
34
Explain how the Kanban system helps reduce inventories.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
35
EOQ, Safety Stock, Lead Time, Batch Size, and JIT
Bateman Company produces helmets for drivers of motorcycles. Helmets are produced in batches according to model and size. Although the setup and production time vary for each model, the smallest lead time is six days. The most popular model, Model HA2, takes two days for setup, and the production rate is 750 units per day. The expected annual demand for the model is 36,000 units. Demand for the model, however, can reach 45,000 units. The cost of carrying one HA2 helmet is $3 per unit. The setup cost is $6,000. Bateman chooses its batch size based on the economic order quantity criterion. Expected annual demand is used to compute the EOQ.
Recently, Bateman has encountered some stiff competition-especially from foreign sources. Some of the foreign competitors have been able to produce and deliver the helmets to retailers in half the time it takes Bateman to produce. For example, a large retailer recently requested a delivery of 12,000 Model HA2 helmets with the stipulation that the helmets be delivered within seven working days. Bateman had 3,000 units of HA2 in stock. Bateman informed the potential customer that it could deliver 3,000 units immediately and the other 9,000 units in about 14 working days-with the possibility of interim partial orders being delivered. The customer declined the offer indicating that the total order had to be delivered within seven working days so that its stores could take advantage of some special local conditions. The customer expressed regret and indicated that it would accept the order from another competitor who could satisfy the time requirements.
Required:
1. Calculate the optimal batch size for Model HA2 using the EOQ model. Was Bateman's response to the customer right? Would it take the time indicated to produce the number of units wanted by the customer? Explain with supporting computations.
2. Upon learning of the lost order, the marketing manager grumbled about Bateman's inventory policy, "We lost the order because we didn't have sufficient inventory. We need to carry more units in inventory to deal with unexpected orders like these." Do you agree or disagree? How much additional inventory would have been needed to meet customer requirements? In the future, should Bateman carry more inventory? Can you think of other solutions?
3. Fenton Gray, the head of industrial engineering, reacted differently to the lost order: "Our problem is more complex than insufficient inventory. I know that our foreign competitors carry much less inventory than we do. What we need to do is decrease the lead time. I have been studying this problem, and my staff has found a way to reduce setup time for Model HA2 from two days to 1.5 hours. Using this new procedure, setup cost can be reduced to about $94. Also, by rearranging the plant layout for this product-creating what are called manufacturing cells-we can increase the production rate from 750 units per day to about 2,000 units per day. This is done simply by eliminating a lot of move time and waiting time-both non-value-added activities." Assume that the engineer's estimates are on target. Compute the new optimal batch size (using the EOQ formula). What is the new lead time? Given this new information, would Bateman have been able to meet the customer's time requirements? Assume that there are eight hours available in each workday.
4. Suppose that the setup time and cost are reduced to 0.5 hour and $10, respectively. What is the batch size now? As setup time approaches zero and the setup cost becomes negligible, what does this imply? Assume, for example, that it takes five minutes to set up, and costs are about $0.864 per setup.
Bateman Company produces helmets for drivers of motorcycles. Helmets are produced in batches according to model and size. Although the setup and production time vary for each model, the smallest lead time is six days. The most popular model, Model HA2, takes two days for setup, and the production rate is 750 units per day. The expected annual demand for the model is 36,000 units. Demand for the model, however, can reach 45,000 units. The cost of carrying one HA2 helmet is $3 per unit. The setup cost is $6,000. Bateman chooses its batch size based on the economic order quantity criterion. Expected annual demand is used to compute the EOQ.
Recently, Bateman has encountered some stiff competition-especially from foreign sources. Some of the foreign competitors have been able to produce and deliver the helmets to retailers in half the time it takes Bateman to produce. For example, a large retailer recently requested a delivery of 12,000 Model HA2 helmets with the stipulation that the helmets be delivered within seven working days. Bateman had 3,000 units of HA2 in stock. Bateman informed the potential customer that it could deliver 3,000 units immediately and the other 9,000 units in about 14 working days-with the possibility of interim partial orders being delivered. The customer declined the offer indicating that the total order had to be delivered within seven working days so that its stores could take advantage of some special local conditions. The customer expressed regret and indicated that it would accept the order from another competitor who could satisfy the time requirements.
Required:
1. Calculate the optimal batch size for Model HA2 using the EOQ model. Was Bateman's response to the customer right? Would it take the time indicated to produce the number of units wanted by the customer? Explain with supporting computations.
2. Upon learning of the lost order, the marketing manager grumbled about Bateman's inventory policy, "We lost the order because we didn't have sufficient inventory. We need to carry more units in inventory to deal with unexpected orders like these." Do you agree or disagree? How much additional inventory would have been needed to meet customer requirements? In the future, should Bateman carry more inventory? Can you think of other solutions?
3. Fenton Gray, the head of industrial engineering, reacted differently to the lost order: "Our problem is more complex than insufficient inventory. I know that our foreign competitors carry much less inventory than we do. What we need to do is decrease the lead time. I have been studying this problem, and my staff has found a way to reduce setup time for Model HA2 from two days to 1.5 hours. Using this new procedure, setup cost can be reduced to about $94. Also, by rearranging the plant layout for this product-creating what are called manufacturing cells-we can increase the production rate from 750 units per day to about 2,000 units per day. This is done simply by eliminating a lot of move time and waiting time-both non-value-added activities." Assume that the engineer's estimates are on target. Compute the new optimal batch size (using the EOQ formula). What is the new lead time? Given this new information, would Bateman have been able to meet the customer's time requirements? Assume that there are eight hours available in each workday.
4. Suppose that the setup time and cost are reduced to 0.5 hour and $10, respectively. What is the batch size now? As setup time approaches zero and the setup cost becomes negligible, what does this imply? Assume, for example, that it takes five minutes to set up, and costs are about $0.864 per setup.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
36
What are ordering costs? What are setup costs? What are carrying costs? Provide examples of each type of cost.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
37
REORDER POINT
Baker Company manufactures backpacks. A heavy-duty strap is one part the company orders from an outside supplier. Information pertaining to the strap is as follows:

Required:
1. What is the reorder point assuming no safety stock is carried?
2. What is the reorder point assuming that safety stock is carried?
Baker Company manufactures backpacks. A heavy-duty strap is one part the company orders from an outside supplier. Information pertaining to the strap is as follows:

Required:
1. What is the reorder point assuming no safety stock is carried?
2. What is the reorder point assuming that safety stock is carried?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
38
PRODUCT MIX DECISIONS, MULTIPLE CONSTRAINTS
Cardin Company produces two types of gears: Model 12 and Model 15. Market conditions limit the number of each gear that can be sold. For Model 12, no more than 15,000 units can be sold, and for Model 15, no more than 40,000 units. Each gear must be notched by a special machine. Cardin owns eight machines that together provide 40,000 hours of machine time per year. Each unit of Model 12 requires two hours of machine time, and each unit of Model 15 requires one half-hour of machine time. The unit contribution for Model 12 is $30 and for Model 15 is $15. Cardin wants to identify the product mix that will maximize total contribution margin.
Required:
1. Formulate Cardin's problem as a linear programming model.
2. Solve the linear programming model in Requirement 1.
3. Identify which constraints are binding and which are loose. Also, identify the constraints as internal or external.
Cardin Company produces two types of gears: Model 12 and Model 15. Market conditions limit the number of each gear that can be sold. For Model 12, no more than 15,000 units can be sold, and for Model 15, no more than 40,000 units. Each gear must be notched by a special machine. Cardin owns eight machines that together provide 40,000 hours of machine time per year. Each unit of Model 12 requires two hours of machine time, and each unit of Model 15 requires one half-hour of machine time. The unit contribution for Model 12 is $30 and for Model 15 is $15. Cardin wants to identify the product mix that will maximize total contribution margin.
Required:
1. Formulate Cardin's problem as a linear programming model.
2. Solve the linear programming model in Requirement 1.
3. Identify which constraints are binding and which are loose. Also, identify the constraints as internal or external.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
39
REORDER POINT
Jimbaya Corporation has an EOQ of 2,500 units. The company uses an average of 250 units per day. An order to replenish the part requires a lead time of five days.
Required:
1. Calculate the reorder point, using Equation 20.3.
2. Graphically display the reorder point, where the vertical axis is inventory (units) and the horizontal axis is time (days). Show two replenishments, beginning at time zero with the economic order quantity in inventory.
3. What if the average usage per day of the part is 250 units but a daily maximum usage of 300 units is possible? What is the reorder point when this demand uncertainty exists?
Jimbaya Corporation has an EOQ of 2,500 units. The company uses an average of 250 units per day. An order to replenish the part requires a lead time of five days.
Required:
1. Calculate the reorder point, using Equation 20.3.
2. Graphically display the reorder point, where the vertical axis is inventory (units) and the horizontal axis is time (days). Show two replenishments, beginning at time zero with the economic order quantity in inventory.
3. What if the average usage per day of the part is 250 units but a daily maximum usage of 300 units is possible? What is the reorder point when this demand uncertainty exists?

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
40
Explain how long-term contractual relationships with suppliers can reduce the acquisition cost of materials.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck
41
Product Mix Decision, Single and Multiple Constraints
Taylor Company produces two industrial cleansers that use the same liquid chemical input: Pocolimpio and Maslimpio. Pocolimpio uses two quarts of the chemical for every unit produced, and Maslimpio uses five quarts. Currently, Taylor has 6,000 quarts of the material in inventory. All of the material is imported. For the coming year, Taylor plans to import 6,000 quarts to produce 1,000 units of Pocolimpio and 2,000 units of Maslimpio. The detail of each product's unit contribution margin is as follows:
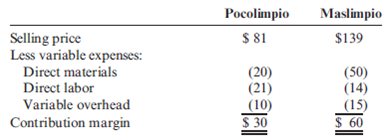
Taylor Company has received word that the source of the material has been shut down by embargo. Consequently, the company will not be able to import the 6,000 quarts it planned to use in the coming year's production. There is no other source of the material.
Required:
1. Compute the total contribution margin that the company would earn if it could import the 6,000 quarts of the material.
2. Determine the optimal usage of the company's inventory of 6,000 quarts of the material. Compute the total contribution margin for the product mix that you recommend.
3. Assume that Pocolimpio uses three direct labor hours for every unit produced and that Mas- limpio uses two hours. A total of 6,000 direct labor hours is available for the coming year.
a. Formulate the linear programming problem faced by Taylor Company. To do so, you must derive mathematical expressions for the objective function and for the materials and labor constraints.
b. Solve the linear programming problem using the graphical approach.
c. Compute the total contribution margin produced by the optimal mix.
Taylor Company produces two industrial cleansers that use the same liquid chemical input: Pocolimpio and Maslimpio. Pocolimpio uses two quarts of the chemical for every unit produced, and Maslimpio uses five quarts. Currently, Taylor has 6,000 quarts of the material in inventory. All of the material is imported. For the coming year, Taylor plans to import 6,000 quarts to produce 1,000 units of Pocolimpio and 2,000 units of Maslimpio. The detail of each product's unit contribution margin is as follows:

Taylor Company has received word that the source of the material has been shut down by embargo. Consequently, the company will not be able to import the 6,000 quarts it planned to use in the coming year's production. There is no other source of the material.
Required:
1. Compute the total contribution margin that the company would earn if it could import the 6,000 quarts of the material.
2. Determine the optimal usage of the company's inventory of 6,000 quarts of the material. Compute the total contribution margin for the product mix that you recommend.
3. Assume that Pocolimpio uses three direct labor hours for every unit produced and that Mas- limpio uses two hours. A total of 6,000 direct labor hours is available for the coming year.
a. Formulate the linear programming problem faced by Taylor Company. To do so, you must derive mathematical expressions for the objective function and for the materials and labor constraints.
b. Solve the linear programming problem using the graphical approach.
c. Compute the total contribution margin produced by the optimal mix.

Unlock Deck
Unlock for access to all 41 flashcards in this deck.
Unlock Deck
k this deck


