Deck 14: Experimental Designonline Only
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/64
Play
Full screen (f)
Deck 14: Experimental Designonline Only
1
In a factorial experiment, all possible treatment combinations of the various levels of the factors under study are examined.
True
2
In an observational study, information from a population of interest is gathered without any attempt on the part of those conducting the study to influence the population or to intervene in any way.
True
3
Blocking is a way to reduce or eliminate within-groups variation.
True
4
A factorial design allows us to examine potentially important interactions among the independent variables.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
5
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 5 treatment groups, 16 blocks.The treatments F value (Fstat) turns out to be 6.253.In determining the p-value for this result, you should use df1 = 4 and df2 = 15.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
6
The independent variables in an experimental study are called factors.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
7
A completely randomized design is an extension of the matched samples approach.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
8
In an experimental study the investigator has no ability to directly influence or manipulate any of the elements involved in the investigation.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
9
In an experiment using a randomized complete block design, if the p-value for Fstat is greater than the significance level of the test, we can conclude that one of more of the treatment means is different from the others.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
10
In an experiment using a randomized complete block design, if the p-value for Fstat is less than the significance level of the test, we can conclude that one of more of the treatment means is different from the others.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
11
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 3 treatment groups and 9 blocks.The treatments F value (Fstat) turns out to be 5.080.In determining the p-value for this result, you should use df1 = 2 and df2 = 16.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
12
In an experiment using a randomized complete block design we usually don't test to see if there are statistically significant differences between block means.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
13
In an experiment using a randomized complete block design, if the value of Fstat is less than the critical value of F ( Fc or Fcrit) for the test, we can conclude that one of more of the treatment means is different from the others.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
14
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 5 treatment groups, 15 blocks.The error sum of squares (SSE) value is 2800.The mean square error (MSE) value must be 50.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
15
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 3 treatment groups, 8 blocks and 24 experimental units.The degrees of freedom that you should assign to the blocks sum of squares is 16.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
16
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 2 treatment groups, 20 blocks.The treatments F value (Fstat) turns out to be 3.662.In finding the critical F value to use in an "equal treatment means" hypothesis test here, you should use df1 = 1 and df2 = 19.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
17
Treatments are the various states or levels that an experimental factor can take on.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
18
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 4 treatment groups and 10 blocks.The degrees of freedom that you should use to compute the mean square error (MSE) is 27.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
19
The dependent variable in an experimental study is called a response variable.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
20
In a randomized complete block design, experimental units are matched according to a similarity of characteristics.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
21
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two Factor A treatments, five Factor B treatments, and three replications.In finding the critical F value to use in testing the significance of the Factor A effect, you should use df1 = 1 and df2 = 20.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
22
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are three treatments for Factor A and four treatments for Factor B.Four replications are being used for each factor combination.The degrees of freedom that you should assign to the interaction sum of squares is 6.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
23
A study in which the investigator has the ability to directly influence or manipulate any of the elements involved in the investigation is called a(n)
A)observational study
B)census study
C)experimental study
D)replicated study
E)gratuitous study
A)observational study
B)census study
C)experimental study
D)replicated study
E)gratuitous study

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
24
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two treatments for Factor A and three treatments for Factor B.Two replications are being used for each factor combination.The degrees of freedom that you should use to compute the Factor B mean square value is 2.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
25
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 4 treatment groups and 10 blocks.The error sum of squares value is 5400.The mean square error value must be
A)122.22
B)540
C)1800
D)135
E)200
A)122.22
B)540
C)1800
D)135
E)200

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
26
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two Factor A treatments, four Factor B treatments, and three replications.The interaction sum of squares value turns out to be 6000.The interaction mean square value must be 750.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
27
The various states or levels that an experimental factor can take on are called
A)x factors
B)y factors
C)repetitions
D)treatments
E)experimental units
A)x factors
B)y factors
C)repetitions
D)treatments
E)experimental units

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
28
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two Factor A treatments, five Factor B treatments, and two replications.The F value (Fstat) for Factor B turns out to be 4.662.In determining the p-value for this result, you should use df1 = 4 and df2 = 10.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
29
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 4 treatment groups and 6 blocks.The number of experimental units is
A)15
B)10
C)18
D)24
E)36
A)15
B)10
C)18
D)24
E)36

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
30
The dependent variable in an experimental study is called a(n)
A)x variable
B)index variable
C)extraneous factor
D)dummy factor
E)response variable
A)x variable
B)index variable
C)extraneous factor
D)dummy factor
E)response variable

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
31
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are three treatments for Factor A and four treatments for Factor B.Two replications are being used for each factor combination.The degrees of freedom that you should use to compute the mean square error (MSE) value is 12.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
32
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 5 treatment groups, 9 blocks.The degrees of freedom that you should assign to the error sum of squares is
A)45
B)32
C)14
D)24
E)12
A)45
B)32
C)14
D)24
E)12

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
33
An experimental design that represents an extension of the matched samples idea is a(n)
A)completely randomized design
B)randomized block design
C)factorial design
D)observational design
E)graphic design
A)completely randomized design
B)randomized block design
C)factorial design
D)observational design
E)graphic design

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
34
The independent variables in an experimental study are called
A)factors
B)objectives
C)y variables
D)treatments
E)extraneous variables
A)factors
B)objectives
C)y variables
D)treatments
E)extraneous variables

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
35
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 3 treatment groups and 12 blocks.The error sum of squares value is 4400.The mean square error value must be
A)122.22
B)200
C)146.67
D)440
E)400
A)122.22
B)200
C)146.67
D)440
E)400

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
36
A study in which information from a population of interest is gathered without any attempt on the part of those conducting the study to influence the population or to intervene in any way is called a(n)
A)statistical study
B)experimental study
C)hands-free study
D)longitudinal study
E)observational study
A)statistical study
B)experimental study
C)hands-free study
D)longitudinal study
E)observational study

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
37
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are three treatments for Factor A and five treatments for Factor B.Two replications are being used for each factor combination.Total sample size must be 15.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
38
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are three treatments for Factor A and four treatments for Factor B.Two replications are being used for each factor combination.The degrees of freedom that you should assign to the error sum of squares is 12.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
39
In a randomized complete block design, we routinely test whether the effect of one factor on the response variable depends on the level of another factor.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
40
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two Factor A treatments, five Factor B treatments, and two replications.The p-value for Factor B turns out to be .026.If the significance level for the test is set at 5%, we can conclude that the Factor B be effect is not statistically significant.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
41
An experimental design that allows us to examine potentially important interactions among the independent variables is a(n)
A)repetitious design
B)block design
C)factorial design
D)interactive design
E)none of the above
A)repetitious design
B)block design
C)factorial design
D)interactive design
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
42
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 5 treatment groups and 6 blocks.If the significance level for the F test you will use to test for a difference in treatment means is 5%, the critical F value (Fc or Fcrit) for the test is
A)2.534
B)2.866
C)2.690
D)2.711
E)4.431
A)2.534
B)2.866
C)2.690
D)2.711
E)4.431

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
43
In a factorial experiment,
A)all possible treatment combinations of the various levels of the factors under study are examined.
B)we can test for interactions
C)we can examine the role of multiple factors
D)we can establish whether a factor effect is statistically significant
E)all of the above
A)all possible treatment combinations of the various levels of the factors under study are examined.
B)we can test for interactions
C)we can examine the role of multiple factors
D)we can establish whether a factor effect is statistically significant
E)all of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
44
Below is some of the ANOVA information for an experiment using a randomized complete block design.In the experiment, there are three treatment groups and nine blocks.Report the indicated critical F value if the significance level for the test is set at 5%. 
A)15.303
B)3.634
C)11.726
D)6.240
E)2.115

A)15.303
B)3.634
C)11.726
D)6.240
E)2.115

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
45
In a two-factor factorial experiment, there are four treatments for Factor A and five treatments for Factor B.Two replications are being used for each factor combination.Total sample size here
A)20
B)24
C)60
D)12
E)40
A)20
B)24
C)60
D)12
E)40

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
46
Below is some of the ANOVA information for an experiment using a randomized complete block design.In the experiment, there are two treatment groups and five blocks.Report the indicated F value in the partially completed ANOVA table. 
A)2.565
B)1.291
C)60
D)12
E)6.456

A)2.565
B)1.291
C)60
D)12
E)6.456

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
47
Below are the results from an experiment using a randomized complete block design. 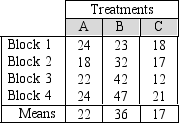 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below:
 Report the treatments sum of squares here.
Report the treatments sum of squares here.
A)776
B)632
C)388
D)316
E)none of the above
 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below: Report the treatments sum of squares here.
Report the treatments sum of squares here.A)776
B)632
C)388
D)316
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
48
Below are the results from an experiment using a randomized complete block design. 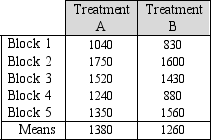 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below:
 Report the treatments mean square here.
Report the treatments mean square here.
A)24000
B)22050
C)36000
D)31650
E)none of the above
 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below: Report the treatments mean square here.
Report the treatments mean square here.A)24000
B)22050
C)36000
D)31650
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
49
Below are the results from an experiment using a randomized complete block design. 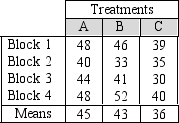 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below:
 Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
A)12.74, Reject the no difference in treatment means null hypothesis
B)7.12, Reject the no difference in treatment means null hypothesis
C)3.62, Do not reject the no difference in treatment means null hypothesis
D)5.96, Reject the no difference in treatment means null hypothesis
E)1.40, Do not reject the no difference in treatment means null hypothesis
 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below: Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.A)12.74, Reject the no difference in treatment means null hypothesis
B)7.12, Reject the no difference in treatment means null hypothesis
C)3.62, Do not reject the no difference in treatment means null hypothesis
D)5.96, Reject the no difference in treatment means null hypothesis
E)1.40, Do not reject the no difference in treatment means null hypothesis

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
50
Testing whether the effect of one factor on the response variable depends on the level of another factor means we are testing
A)replications
B)experimental units
C)factorials
D)interactions
E)extraneous variables
A)replications
B)experimental units
C)factorials
D)interactions
E)extraneous variables

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
51
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 3 treatment groups and 8 blocks.The treatment sum of squares is 7200.The error sum of squares value is 4200.The F value (Fstat) that will be used to test the "equal treatment means" null hypothesis is
A)12.00
B)6.00
C)14.667
D)4.222
E)400.333
A)12.00
B)6.00
C)14.667
D)4.222
E)400.333

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
52
Below is some of the ANOVA information for an experiment using a randomized complete block design.In the experiment, there are four treatment groups and five blocks.Report the indicated F value in the partially completed ANOVA table. 
A)2.50
B)12.20
C)4.80
D)6.24
E)8.00

A)2.50
B)12.20
C)4.80
D)6.24
E)8.00

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
53
You are filling in the ANOVA table values for an experiment using a two-factor factorial design.In the experiment, there are two treatments for Factor A and three treatments for Factor B.Two replications are being used for each factor combination.The degrees of freedom that you should assign to the Factor B sum of squares is
A)3
B)2
C)4
D)5
E)6
A)3
B)2
C)4
D)5
E)6

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
54
Below is a partially complete ANOVA table from an experiment using a randomized complete block design.Report the appropriate Fstat to use in determining whether you can you reject the null hypothesis that there is no difference in the treatment means for the populations represented.Use a significance level of 5% and state your conclusion. 
A)10.074, Reject the no difference in treatment means null hypothesis
B)8.135, Reject the no difference in treatment means null hypothesis
C)3.622, Do not reject the no difference in treatment means null hypothesis
D)4.295, Do not reject the no difference in treatment means null hypothesis
E)None of the above.

A)10.074, Reject the no difference in treatment means null hypothesis
B)8.135, Reject the no difference in treatment means null hypothesis
C)3.622, Do not reject the no difference in treatment means null hypothesis
D)4.295, Do not reject the no difference in treatment means null hypothesis
E)None of the above.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
55
An experimental design in which all possible treatment combinations of the various levels of the factors under study are examined is called a(n)
A)cross-tabs design
B)observational study
C)factorial design
D)block design
E)representative study
A)cross-tabs design
B)observational study
C)factorial design
D)block design
E)representative study

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
56
An experimental design that allows us to examine potentially important interactions among the independent variables is a(n)
A)cross-tabs design
B)observational design
C)factorial design
D)block design
E)time series design
A)cross-tabs design
B)observational design
C)factorial design
D)block design
E)time series design

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
57
Below are the results from an experiment using a randomized complete block design. 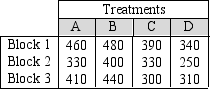 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below:
 Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
A)18.078, Reject the no difference in treatment means null hypothesis
B)2.444, Do not reject the no difference in treatment means null hypothesis
C)12.740, Reject the no difference in treatment means null hypothesis
D)3.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above
 Part of the ANOVA table for the results is shown below:
Part of the ANOVA table for the results is shown below: Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.
Report the appropriate Fstat value for the test of treatment means and your conclusion.The significance level for the test is set at 5%.A)18.078, Reject the no difference in treatment means null hypothesis
B)2.444, Do not reject the no difference in treatment means null hypothesis
C)12.740, Reject the no difference in treatment means null hypothesis
D)3.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
58
Below is some of the ANOVA information for an experiment using a randomized complete block design.In the experiment, there are four treatment groups and six blocks.The significance level for the test is set at 5%.Report the indicated F value and your conclusion. 
A)4.307, Reject the no difference in treatment means null hypothesis
B)1.634, Do not reject the no difference in treatment means null hypothesis
C)11.726, Reject the no difference in treatment means null hypothesis
D)5.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above

A)4.307, Reject the no difference in treatment means null hypothesis
B)1.634, Do not reject the no difference in treatment means null hypothesis
C)11.726, Reject the no difference in treatment means null hypothesis
D)5.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
59
You are filling in the ANOVA table values for an experiment using a randomized complete block design.In the experiment, there are 5 treatment groups and 9 blocks.The treatment sum of squares is 6400.The error sum of squares value is 32000.The F value (Fstat) that will be used to test the "equal treatment means" null hypothesis is
A)1.60
B)1600
C)10.00
D)3.20
E).200
A)1.60
B)1600
C)10.00
D)3.20
E).200

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
60
Below is some of the ANOVA information for an experiment using a randomized complete block design.In the experiment, there are four treatment groups and four blocks.The significance level for the test is set at 1%.Report the indicated F value and your conclusion. 
A)7.324, Do not reject the no difference in treatment means null hypothesis
B)2.444, Reject the no difference in treatment means null hypothesis
C)9.526, Reject the no difference in treatment means null hypothesis
D)3.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above

A)7.324, Do not reject the no difference in treatment means null hypothesis
B)2.444, Reject the no difference in treatment means null hypothesis
C)9.526, Reject the no difference in treatment means null hypothesis
D)3.240, Do not reject the no difference in treatment means null hypothesis
E)none of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
61
Below is some of the ANOVA information for a two-factor factorial experiment.Compute the appropriate Fstat value and indicate whether results here show a significant interaction effect at the 5% significance level. 
A)2.77; results do not show a significant interaction effect at the 5% significance level.
B)1.83; results do not show a significant interaction effect at the 5% significance level.
C)5.50; results show a significant interaction effect at the 5% significance level.
D)6.52; results show a significant interaction effect at the 5% significance level.
E)None of the above

A)2.77; results do not show a significant interaction effect at the 5% significance level.
B)1.83; results do not show a significant interaction effect at the 5% significance level.
C)5.50; results show a significant interaction effect at the 5% significance level.
D)6.52; results show a significant interaction effect at the 5% significance level.
E)None of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
62
Below is some of the ANOVA information for a two-factor factorial experiment.Compute the appropriate Fstat value and indicate whether results here show a significant Factor B effect at the 5% significance level. 
A)11.45; results show a significant Factor B effect at the 5% significance level.
B)3.26; results do not show a significant Factor B effect at the 5% significance level.
C)2.23; results do not show a significant Factor B effect at the 5% significance level.
D)8.58; results show a significant Factor B effect at the 5% significance level.
E)None of the above

A)11.45; results show a significant Factor B effect at the 5% significance level.
B)3.26; results do not show a significant Factor B effect at the 5% significance level.
C)2.23; results do not show a significant Factor B effect at the 5% significance level.
D)8.58; results show a significant Factor B effect at the 5% significance level.
E)None of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
63
Below is some of the ANOVA information for a two-factor factorial experiment.Compute the appropriate Fstat value and indicate whether results here show a significant Factor A effect at the 5% significance level. 
A)15.00; results show a significant Factor A effect at the 5% significance level.
B)3.50; results do not show a significant Factor A effect at the 5% significance level.
C)7.40; results show a significant Factor A effect at the 5% significance level.
D)2.10; results do not show a significant Factor A effect at the 5% significance level.
E)None of the above

A)15.00; results show a significant Factor A effect at the 5% significance level.
B)3.50; results do not show a significant Factor A effect at the 5% significance level.
C)7.40; results show a significant Factor A effect at the 5% significance level.
D)2.10; results do not show a significant Factor A effect at the 5% significance level.
E)None of the above

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck
64
Below is some of the ANOVA information for a two-factor factorial experiment in which the significance level is set at 5%.Indicate which, if any, of the following conclusions are supported by the information in the table. 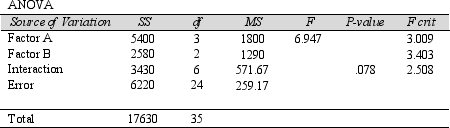
A)The Factor A effect is not statistically significant.
B)The interaction effect is statistically significant.
C)The Factor B effect is statistically significant.
D)The Factor B effect is not statistically significant.
E)None of the above.

A)The Factor A effect is not statistically significant.
B)The interaction effect is statistically significant.
C)The Factor B effect is statistically significant.
D)The Factor B effect is not statistically significant.
E)None of the above.

Unlock Deck
Unlock for access to all 64 flashcards in this deck.
Unlock Deck
k this deck


