Deck 8: Interval Estimates for Proportions, Mean Differences and Proportion Differences
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 8: Interval Estimates for Proportions, Mean Differences and Proportion Differences
1
In a 95% confidence interval estimate of a population proportion, the margin of error will be 2.33 times the standard error of the proportion.
False
2
In a matched sample design, one uses the average for each pair of data values when building a confidence interval.
False
3
An interval estimate of a population proportion is a range of values used to estimate the population parameter .
True
4
As the sample size increases, the margin of error in an interval estimate of a population proportion decreases.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
In a 95% confidence interval estimate of the difference between two population means, the standard error of the proportion will be 1.96 times the margin of error.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
In the absence of any other information, determining the largest sample size that might be necessary to build a 95% confidence interval estimate of a population proportion requires us to assume that the population proportion is .50.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
For the sampling distribution of the sample proportion, the distribution is approximately normal as long as n < 30.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
For large enough sample sizes, 95% of the possible sample mean differences will be within 1.96 standard errors of the population mean difference.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
The value of that maximizes the product (1 - ) is .05.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10
When each data value in one sample is paired with a corresponding data value in another sample, the samples are said to be independent.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
A matched sample design can lead to a smaller sampling error than the independent sample design because some or all of the variation between sampled items is eliminated as a source of sampling error.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
The sampling distribution of the sample mean difference is the probability distribution of all possible values of the sample mean difference when a sample of size n1 is taken from one population and a sample of size n2 is taken from another.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13
A 95% confidence interval estimate of the difference between two population proportions will contain 95% of the possible sample proportion differences.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
14
One of the properties of the sampling distribution of the sample proportion is that the expected value of the sample proportion will be exactly equal to 0.5.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
When calculating the sample size to use in estimating a population proportion, using a proportion equal to 0.25 will provide the maximum sample size.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16
In any confidence interval estimate of a population proportion difference, the margin of error will be less than the standard error of the sampling distribution.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
As the confidence requirement increases, the standard error term in an interval estimate of the difference between two population proportions decreases.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
The sampling distribution of the sample proportion is the probability distribution of all possible values of the sample proportion when a sample of size n is taken from a particular population.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
In determining a confidence interval for the difference between two population proportions, the point estimate of the difference is ( 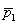 -
- 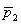 ).
).
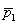 -
- 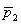 ).
).
Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


