Deck 10: Conics, Parametric Equations, and Polar Coordinates
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/114
Play
Full screen (f)
Deck 10: Conics, Parametric Equations, and Polar Coordinates
1
Find the corresponding rectangular coordinates for the point 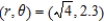 . Round your answer to three decimal places.
. Round your answer to three decimal places.
A)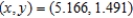
B)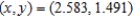
C)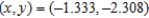
D)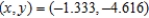
E)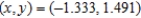
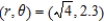 . Round your answer to three decimal places.
. Round your answer to three decimal places.A)
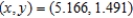
B)
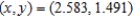
C)
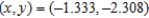
D)
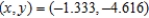
E)
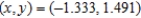
E
2
Match the graph with its polar equation. 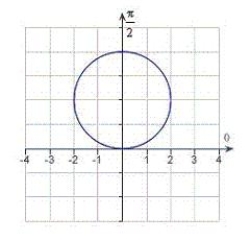
A)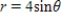
B)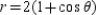
C)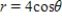
D)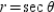
E)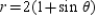

A)
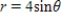
B)
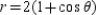
C)
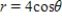
D)
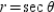
E)
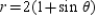
A
3
Find the second derivative 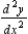 of the parametric equations
of the parametric equations 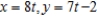 . Round your answer to two decimal places, if necessary.
. Round your answer to two decimal places, if necessary.
A) 0
B) 0.88
C)
D) 1.14
E)
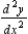 of the parametric equations
of the parametric equations 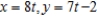 . Round your answer to two decimal places, if necessary.
. Round your answer to two decimal places, if necessary.A) 0
B) 0.88
C)

D) 1.14
E)

A
4
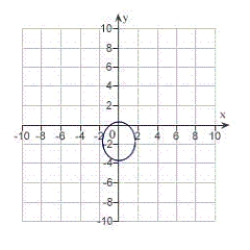
Find the eccentricity and distance from the pole to the directrix of the conic. Then sketch and identify the graph. Use a graphing utility to confirm your results. 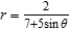
A) eccentricity:
Distance from pole to directrix:
The graph is an ellipse.
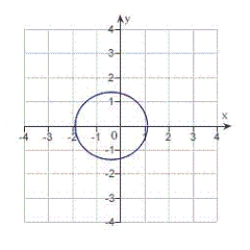
B) eccentricity:
Distance from pole to directrix:
The graph is a hyperbola.
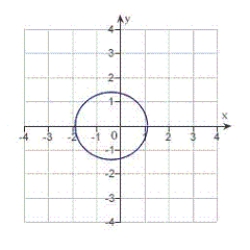
C) eccentricity:
Distance from pole to directrix:
The graph is a hyperbola.
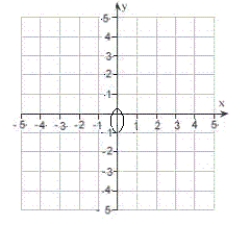
D) eccentricity:
Distance from pole to directrix:
The graph is an ellipse.
E) eccentricity:
Distance from pole to directrix:
The graph is an ellipse.
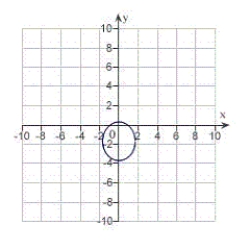
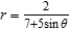
A) eccentricity:

Distance from pole to directrix:

The graph is an ellipse.

B) eccentricity:

Distance from pole to directrix:

The graph is a hyperbola.

C) eccentricity:

Distance from pole to directrix:

The graph is a hyperbola.

D) eccentricity:

Distance from pole to directrix:

The graph is an ellipse.

E) eccentricity:

Distance from pole to directrix:

The graph is an ellipse.


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
5
Find all points (if any) of horizontal and vertical tangency to the curve 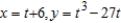 .
.
A) horizontal tangents: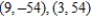 , vertical tangent: none
, vertical tangent: none
B) horizontal tangent: none, vertical tangents: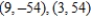
C) horizontal tangents: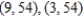 , vertical tangent: none
, vertical tangent: none
D) horizontal tangent: none, vertical tangents: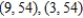
E) horizontal tangent: none, vertical tangent: none
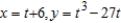 .
.A) horizontal tangents:
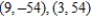 , vertical tangent: none
, vertical tangent: noneB) horizontal tangent: none, vertical tangents:
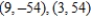
C) horizontal tangents:
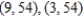 , vertical tangent: none
, vertical tangent: noneD) horizontal tangent: none, vertical tangents:
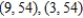
E) horizontal tangent: none, vertical tangent: none

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
6
Find the eccentricity of the ellipse given by 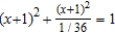 .
.
A)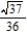
B)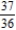
C)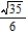
D)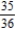
E)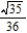
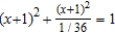 .
.A)
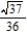
B)
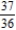
C)
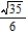
D)
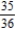
E)
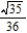

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
7
Match the equation with its graph. 
A)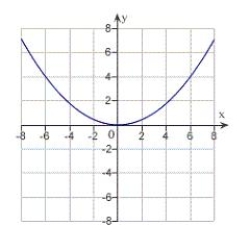
B)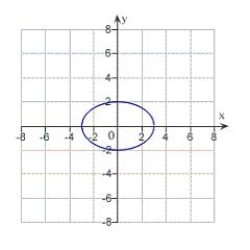
C)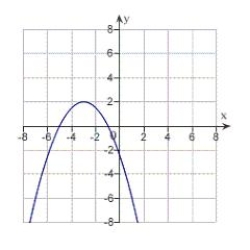
D)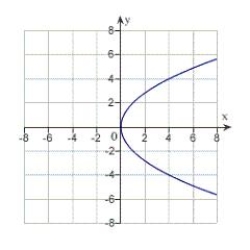
E)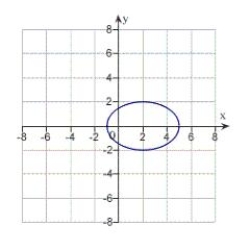

A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
8
For the given point in rectangular coordinates, find two sets of polar coordinates for the point for 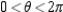 .
. 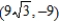
A)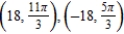
B)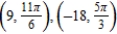
C)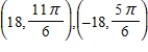
D)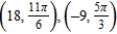
E)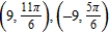
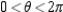 .
. 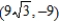
A)
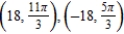
B)
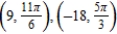
C)
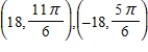
D)
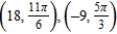
E)
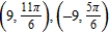

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
9
Identify the graph for the polar equation 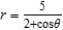 .
.
A)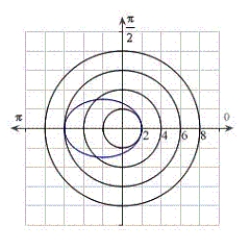
B)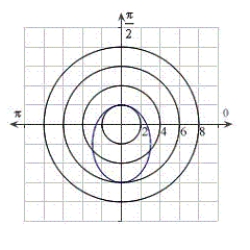
C)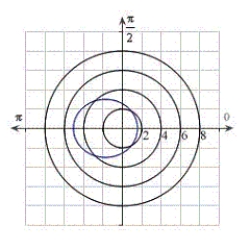
D)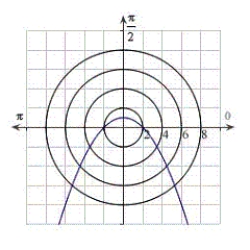
E)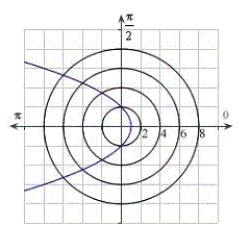
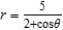 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
10
Find the area of the surface generated by revolving the curve about the given axis. 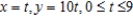 (i) x-axis; (ii) y-axis
(i) x-axis; (ii) y-axis
A)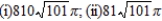
B)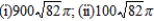
C)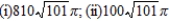
D)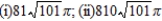
E)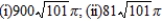
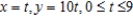 (i) x-axis; (ii) y-axis
(i) x-axis; (ii) y-axisA)
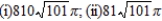
B)
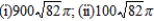
C)
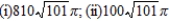
D)
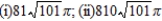
E)
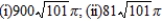

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
11
Match the graph with its polar equation. 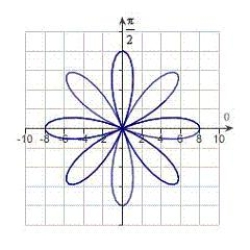
A)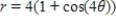
B)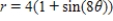
C)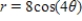
D)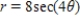
E)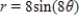

A)
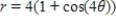
B)
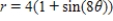
C)
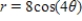
D)
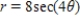
E)
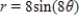

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
12
Find two sets of polar coordinates for the point 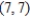 for
for 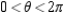 .
.
A)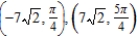
B)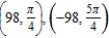
C)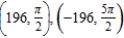
D)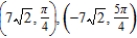
E)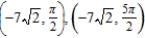
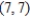 for
for 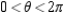 .
.A)
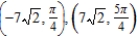
B)
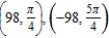
C)
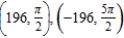
D)
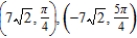
E)
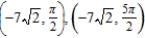

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
13
Match the equation with its graph. 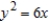
A)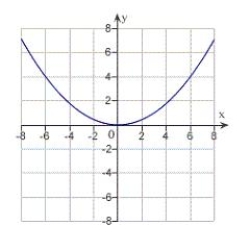
B)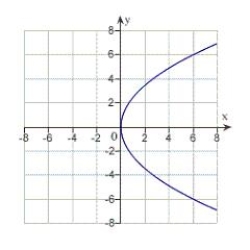
C)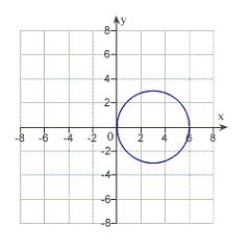
D)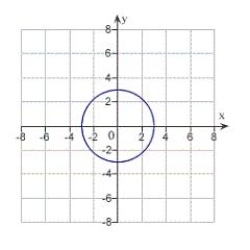
E)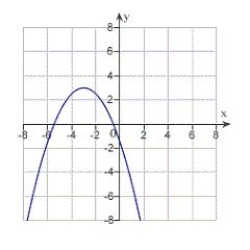
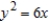
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
14
Find the eccentricity and distance from the pole to the directrix of the conic. Then sketch and identify the graph. Use a graphing utility to confirm your results. 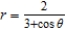
A) eccentricity: distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 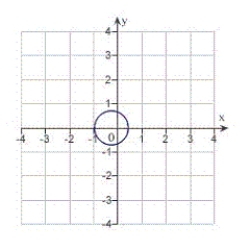
B) eccentricity: distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 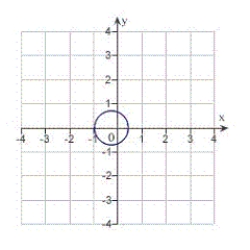
C) eccentricity: distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 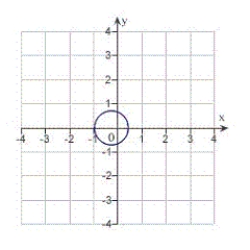
D) eccentricity: distance from pole to directrix:
distance from pole to directrix:  The graph is a hyperbola.
The graph is a hyperbola. 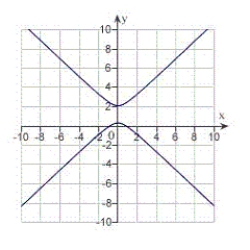
E) eccentricity: distance from pole to directrix:
distance from pole to directrix:  The graph is a hyperbola.
The graph is a hyperbola. 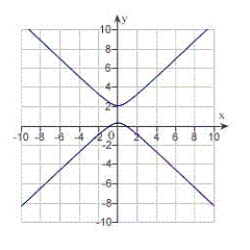
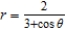
A) eccentricity:
 distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 
B) eccentricity:
 distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 
C) eccentricity:
 distance from pole to directrix:
distance from pole to directrix:  The graph is an ellipse.
The graph is an ellipse. 
D) eccentricity:
 distance from pole to directrix:
distance from pole to directrix:  The graph is a hyperbola.
The graph is a hyperbola. 
E) eccentricity:
 distance from pole to directrix:
distance from pole to directrix:  The graph is a hyperbola.
The graph is a hyperbola. 

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
15
Identify the graph for the polar equation 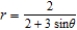 .
.
A)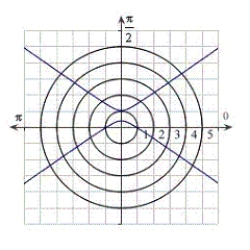
B)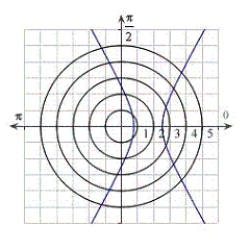
C)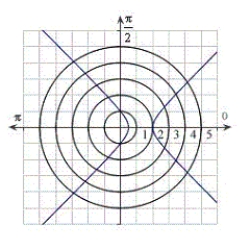
D)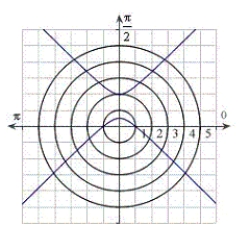
E)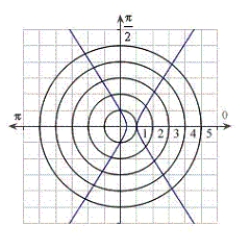
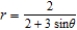 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
16
Match the equation with its graph. 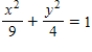
A)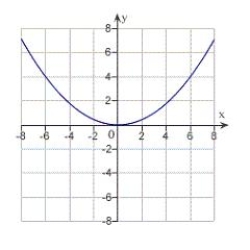
B)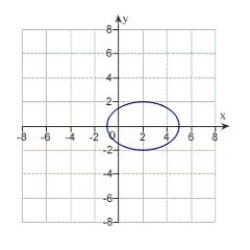
C)
D)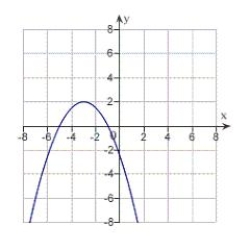
E)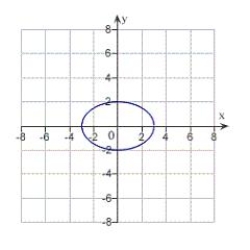
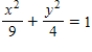
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
17
Identify the graph for the polar equation 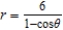 .
.
A)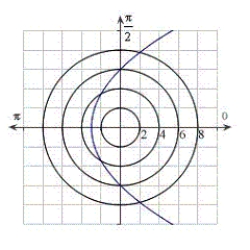
B)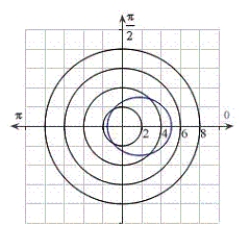
C)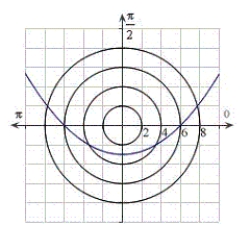
D)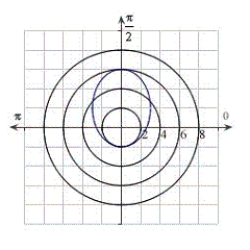
E)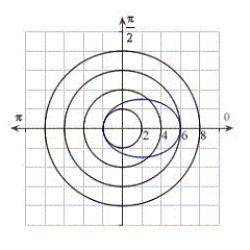
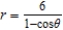 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
18
Match the graph with its polar equation. 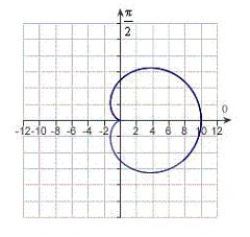
A)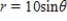
B)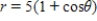
C)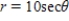
D)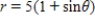
E)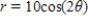

A)
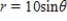
B)
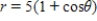
C)
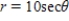
D)
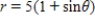
E)
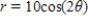

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
19
Match the equation with its graph. 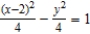
A)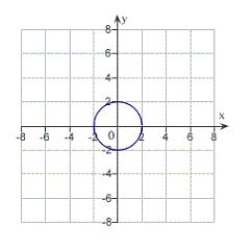
B)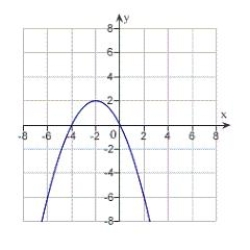
C)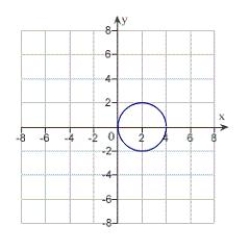
D)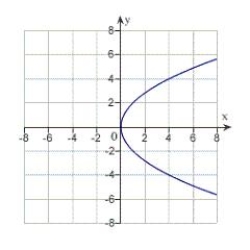
E) none of these
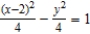
A)

B)

C)

D)

E) none of these

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
20
Find two sets of polar coordinates for the point 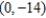 for
for 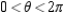 .
.
A)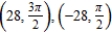
B)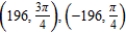
C)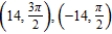
D)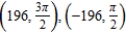
E)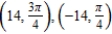
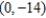 for
for 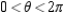 .
.A)
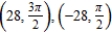
B)
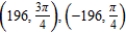
C)
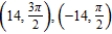
D)
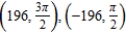
E)
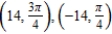

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
21
Find a polar equation for the parabola with its focus at the pole and vertex 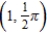 .
.
A)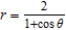
B)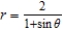
C)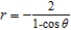
D)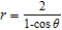
E)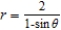
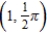 .
.A)
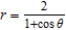
B)
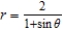
C)
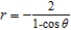
D)
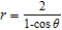
E)
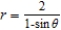

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
22
Find 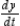 and
and 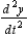 if possible, and find the slope and concavity (if possible) at the point corresponding to t = 2.
if possible, and find the slope and concavity (if possible) at the point corresponding to t = 2. 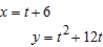
A)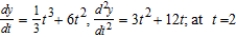 : slope
: slope 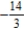 and concave up
and concave up
B)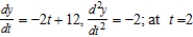 slope 8 and concave down
slope 8 and concave down
C)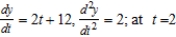 slope 16 and concave up
slope 16 and concave up
D)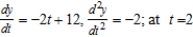 : slope -8 and concave down
: slope -8 and concave down
E)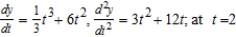 : slope
: slope 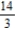 and concave up
and concave up
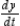 and
and 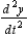 if possible, and find the slope and concavity (if possible) at the point corresponding to t = 2.
if possible, and find the slope and concavity (if possible) at the point corresponding to t = 2. 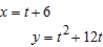
A)
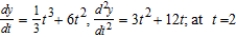 : slope
: slope 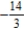 and concave up
and concave upB)
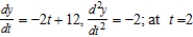 slope 8 and concave down
slope 8 and concave downC)
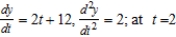 slope 16 and concave up
slope 16 and concave upD)
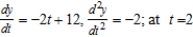 : slope -8 and concave down
: slope -8 and concave downE)
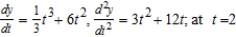 : slope
: slope 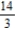 and concave up
and concave up
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
23
Find the center, foci, and vertices of the hyperbola. 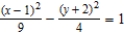
A) center: ; vertices:
; vertices: 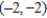 ,
, 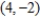 ; foci:
; foci: 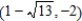 ,
, 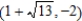 .
.
B) center: ; vertices:
; vertices: 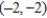 ,
, 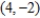 ; foci:
; foci: 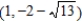 ,
, 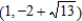 .
.
C) center: ; vertices:
; vertices: 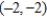 ,
, 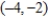 ; foci:
; foci: 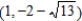 ,
, 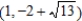 .
.
D) center: ; vertices:
; vertices: 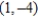 ,
, 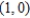 ; foci:
; foci: 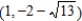 ,
, 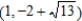 .
.
E) center: ; vertices:
; vertices: 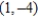 ,
, 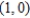 ; foci:
; foci: 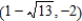 ,
, 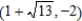 .
.
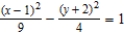
A) center:
 ; vertices:
; vertices: 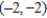 ,
, 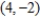 ; foci:
; foci: 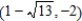 ,
, 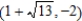 .
.B) center:
 ; vertices:
; vertices: 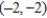 ,
, 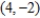 ; foci:
; foci: 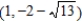 ,
, 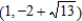 .
.C) center:
 ; vertices:
; vertices: 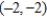 ,
, 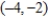 ; foci:
; foci: 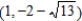 ,
, 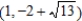 .
.D) center:
 ; vertices:
; vertices: 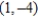 ,
, 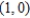 ; foci:
; foci: 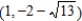 ,
, 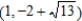 .
.E) center:
 ; vertices:
; vertices: 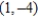 ,
, 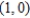 ; foci:
; foci: 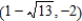 ,
, 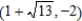 .
.
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
24
Find the eccentricity of the polar equation 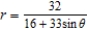 .
.
A)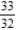
B)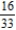
C)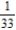
D)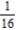
E)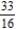
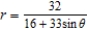 .
.A)
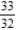
B)
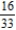
C)
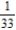
D)
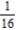
E)
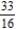

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
25
Find a polar equation for the hyperbola with its focus at the pole, eccentricity 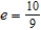 , and directrix
, and directrix  .
.
A)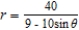
B)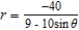
C)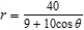
D)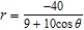
E)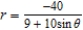
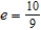 , and directrix
, and directrix  .
.A)
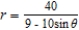
B)
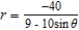
C)
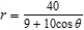
D)
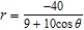
E)
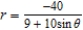

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
26
Find the vertex of the parabola given by  .
.
A)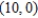
B)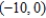
C)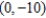
D)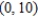
E)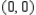
 .
.A)
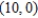
B)
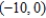
C)
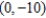
D)
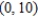
E)
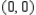

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
27
Find the distance from the pole to the directrix for the conic 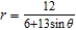 .
.
A)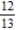
B)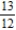
C)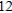
D)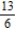
E)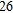
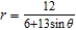 .
. A)
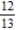
B)
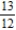
C)
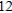
D)
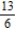
E)
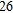

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
28
Find the center of the ellipse given by 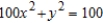 .
.
A)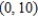
B)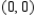
C)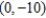
D)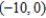
E)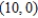
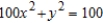 .
.A)
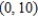
B)
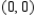
C)
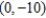
D)
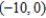
E)
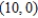

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
29
Find the area of the surface generated by revolving the curve 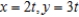 about the x-axis on the interval
about the x-axis on the interval 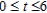 .
.
A)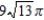
B)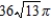
C)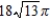
D)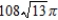
E)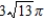
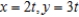 about the x-axis on the interval
about the x-axis on the interval 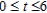 .
.A)
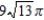
B)
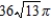
C)
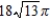
D)
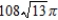
E)
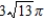

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
30
Identify the conic for the polar equation 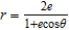 when
when 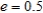 .
.
A) ellipse
B) parabola
C) hyperbola
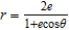 when
when 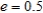 .
.A) ellipse
B) parabola
C) hyperbola

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
31
Find 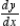 and
and 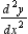 if possible, and find the slope and concavity (if possible) at the point corresponding to
if possible, and find the slope and concavity (if possible) at the point corresponding to 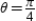 .
. 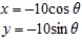
A)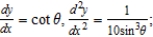 at
at 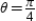 : slope 1 and concave up
: slope 1 and concave up
B)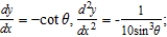 at
at 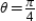 : slope -1 and concave up
: slope -1 and concave up
C)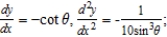 at
at 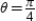 : slope -1 and concave down
: slope -1 and concave down
D)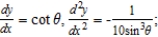 at
at 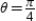 : slope 1 and concave down
: slope 1 and concave down
E)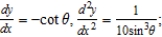 at
at 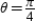 : slope of -1 and concave up
: slope of -1 and concave up
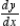 and
and 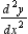 if possible, and find the slope and concavity (if possible) at the point corresponding to
if possible, and find the slope and concavity (if possible) at the point corresponding to 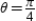 .
. 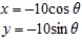
A)
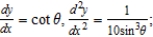 at
at 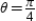 : slope 1 and concave up
: slope 1 and concave upB)
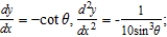 at
at 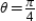 : slope -1 and concave up
: slope -1 and concave upC)
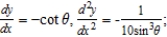 at
at 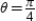 : slope -1 and concave down
: slope -1 and concave downD)
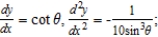 at
at 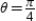 : slope 1 and concave down
: slope 1 and concave downE)
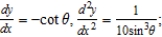 at
at 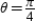 : slope of -1 and concave up
: slope of -1 and concave up
Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
32
Find the second derivative 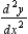 of the parametric equations
of the parametric equations 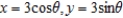 .
.
A)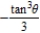
B)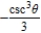
C)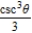
D)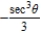
E)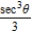
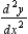 of the parametric equations
of the parametric equations 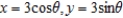 .
. A)
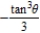
B)
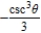
C)
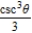
D)
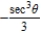
E)
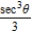

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
33
Classify the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola. 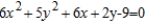
A) parabola
B) ellipse
C) circle
D) hyperbola
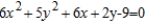
A) parabola
B) ellipse
C) circle
D) hyperbola

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
34
Find an equation of the hyperbola with vertices 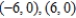 and asymptotes
and asymptotes  .
.
A)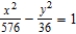
B)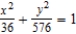
C)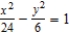
D)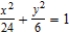
E)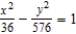
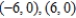 and asymptotes
and asymptotes  .
.A)
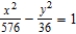
B)
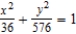
C)
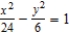
D)
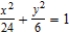
E)
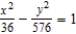

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
35
Find an equation of the parabola with vertex 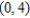 and directrix
and directrix  .
.
A)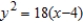
B)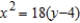
C)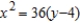
D)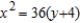
E)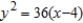
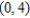 and directrix
and directrix  .
.A)
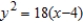
B)
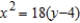
C)
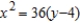
D)
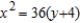
E)
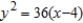

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
36
Find the length of the curve 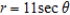 over the interval
over the interval 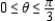 . Round your answer to two decimal places.
. Round your answer to two decimal places.
A) 0.58
B) 19.05
C) 11.00
D) 6.35
E) 1.73
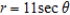 over the interval
over the interval 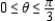 . Round your answer to two decimal places.
. Round your answer to two decimal places. A) 0.58
B) 19.05
C) 11.00
D) 6.35
E) 1.73

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
37
Convert the polar equation to rectangular form. 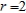
A)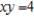
B)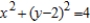
C)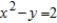
D)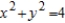
E)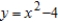
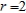
A)
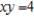
B)
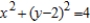
C)
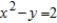
D)
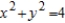
E)
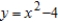

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
38
Find a polar equation for the ellipse with its focus at the pole and vertices 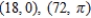 .
.
A)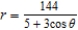
B)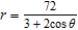
C)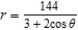
D)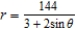
E)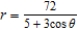
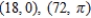 .
.A)
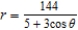
B)
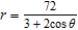
C)
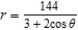
D)
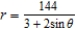
E)
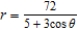

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
39
Find a polar equation for the ellipse with its focus at the pole, eccentricity 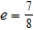 , and directrix
, and directrix  .
.
A)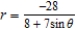
B)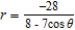
C)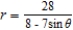
D)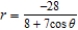
E)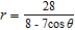
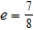 , and directrix
, and directrix  .
.A)
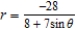
B)
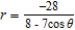
C)
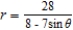
D)
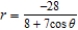
E)
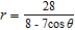

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
40
Find all points (if any) of horizontal and vertical tangency to the curve 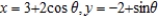 .
.
A) horizontal tangents: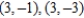 , vertical tangents:
, vertical tangents: 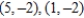
B) horizontal tangents: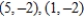 , vertical tangents:
, vertical tangents: 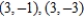
C) horizontal tangent: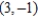 , vertical tangent:
, vertical tangent: 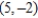
D) horizontal tangents: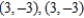 , vertical tangents:
, vertical tangents: 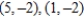
E) horizontal tangent: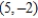 , vertical tangent:
, vertical tangent: 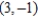
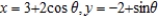 .
.A) horizontal tangents:
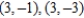 , vertical tangents:
, vertical tangents: 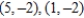
B) horizontal tangents:
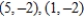 , vertical tangents:
, vertical tangents: 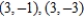
C) horizontal tangent:
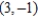 , vertical tangent:
, vertical tangent: 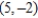
D) horizontal tangents:
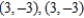 , vertical tangents:
, vertical tangents: 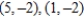
E) horizontal tangent:
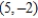 , vertical tangent:
, vertical tangent: 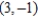

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
41
Find the area of the surface generated by revolving the curve 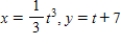 about the y-axis on the interval
about the y-axis on the interval 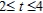 . Round your answer to two decimal places.
. Round your answer to two decimal places.
A) 1436.54
B) 1413.69
C) 1401.46
D) 706.85
E) 2132.77
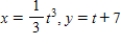 about the y-axis on the interval
about the y-axis on the interval 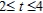 . Round your answer to two decimal places.
. Round your answer to two decimal places. A) 1436.54
B) 1413.69
C) 1401.46
D) 706.85
E) 2132.77

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
42
Find the arc length of the curve on the given interval. 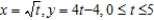
A)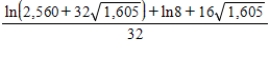
B)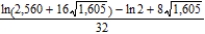
C)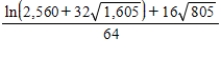
D)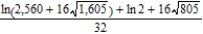
E)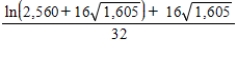
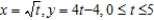
A)
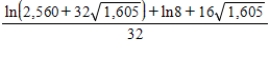
B)
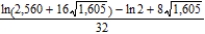
C)
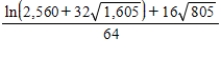
D)
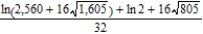
E)
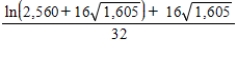

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
43
Find the arc length of the curve on the given interval. 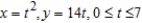
A)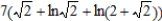
B)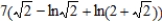
C)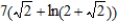
D)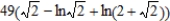
E)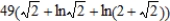
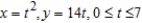
A)
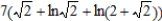
B)
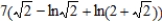
C)
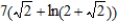
D)
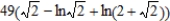
E)
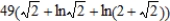

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
44
Determine the t intervals on which the curve 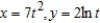 is concave downward or concave upward.
is concave downward or concave upward.
A) concave downward: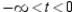 ; concave upward:
; concave upward: 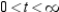
B) concave downward: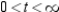 ; concave upward:
; concave upward: 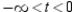
C) concave downward: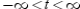
D) concave upward: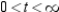
E) concave downward: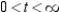
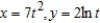 is concave downward or concave upward.
is concave downward or concave upward.A) concave downward:
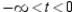 ; concave upward:
; concave upward: 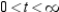
B) concave downward:
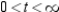 ; concave upward:
; concave upward: 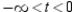
C) concave downward:
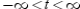
D) concave upward:
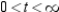
E) concave downward:
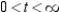

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
45
Use the result, "the set of parametric equations for the line passing through 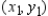 and
and 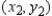 is
is 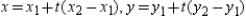 " to find a set of parametric equations for the line passing through
" to find a set of parametric equations for the line passing through 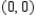 and
and 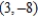 .
.
A)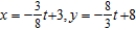
B)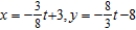
C)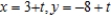
D)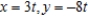
E)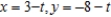
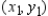 and
and 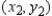 is
is 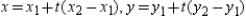 " to find a set of parametric equations for the line passing through
" to find a set of parametric equations for the line passing through 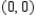 and
and 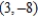 .
.A)
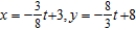
B)
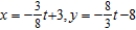
C)
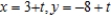
D)
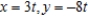
E)
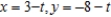

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
46
The path of a projectile is modeled by the parametric equations 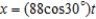 and
and 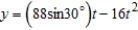 where x and y are measured in feet. Use a graphing utility to approximate the range of the projectile. Round your answer to two decimal places.
where x and y are measured in feet. Use a graphing utility to approximate the range of the projectile. Round your answer to two decimal places.
A) 335.33 ft
B) 558.88 ft
C) 73.76 ft
D) 419.16 ft
E) 209.58 ft
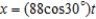 and
and 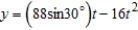 where x and y are measured in feet. Use a graphing utility to approximate the range of the projectile. Round your answer to two decimal places.
where x and y are measured in feet. Use a graphing utility to approximate the range of the projectile. Round your answer to two decimal places.A) 335.33 ft
B) 558.88 ft
C) 73.76 ft
D) 419.16 ft
E) 209.58 ft

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
47
Find the center, foci, vertices, and eccentricity of the ellipse. 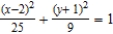
A)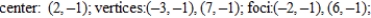
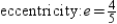
B)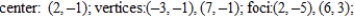
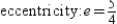
C)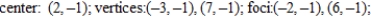
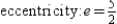
D)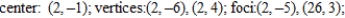
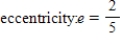
E)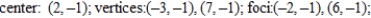
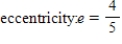
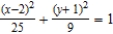
A)
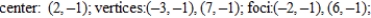
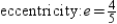
B)
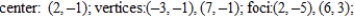
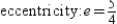
C)
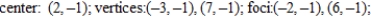
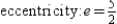
D)
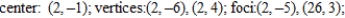
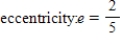
E)
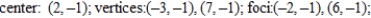
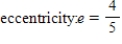

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
48
Find a set of parametric equations for the rectangular equation 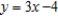 that satisfies the condition
that satisfies the condition 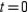 at the point
at the point 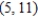 .
.
A)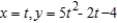
B)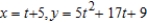
C)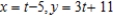
D)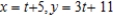
E)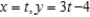
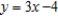 that satisfies the condition
that satisfies the condition 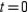 at the point
at the point 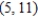 .
.A)
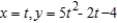
B)
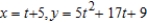
C)
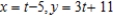
D)
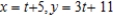
E)
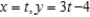

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
49
Convert the polar equation to rectangular form. 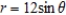
A)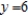
B)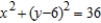
C)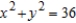
D)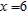
E)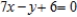
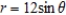
A)
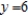
B)
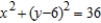
C)
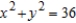
D)
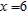
E)
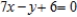

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
50
Identify any points at which the cycloid 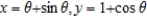 is not smooth.
is not smooth.
A) not smooth when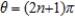
B) smooth everywhere
C) not smooth when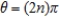
D) not smooth when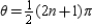
E) not smooth when
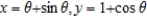 is not smooth.
is not smooth.A) not smooth when
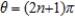
B) smooth everywhere
C) not smooth when
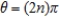
D) not smooth when
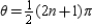
E) not smooth when


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
51
Find all points of intersection of the graphs of the equations. 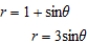
A)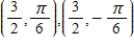
B)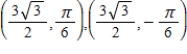
C)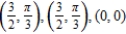
D)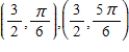
E)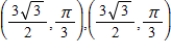
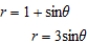
A)
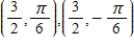
B)
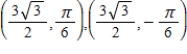
C)
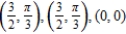
D)
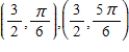
E)
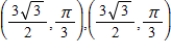

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
52
Write the corresponding rectangular equation for the curve represented by the parametric equations 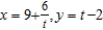 by eliminating the parameter.
by eliminating the parameter.
A)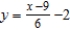
B)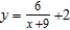
C)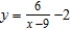
D)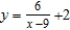
E)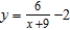
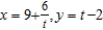 by eliminating the parameter.
by eliminating the parameter.A)
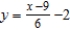
B)
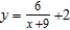
C)
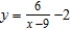
D)
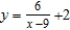
E)
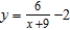

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
53
Write the corresponding rectangular equation for the curve represented by the parametric equations 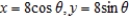 by eliminating the parameter.
by eliminating the parameter.
A)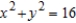
B)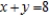
C)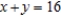
D)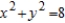
E)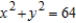
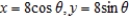 by eliminating the parameter.
by eliminating the parameter.A)
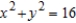
B)
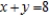
C)
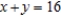
D)
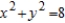
E)
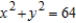

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
54
Find the area of inside 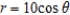 and outside
and outside 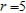 by sketching the graph of the equations using the graphing utility.
by sketching the graph of the equations using the graphing utility.
A)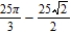
B)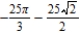
C)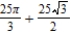
D)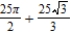
E)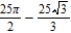
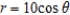 and outside
and outside 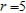 by sketching the graph of the equations using the graphing utility.
by sketching the graph of the equations using the graphing utility. A)
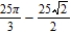
B)
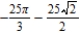
C)
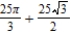
D)
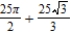
E)
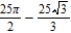

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
55
Find the length of the curve over the given interval. 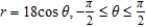
A)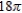
B)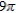
C)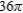
D)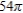
E)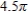
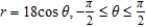
A)
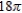
B)
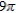
C)
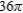
D)
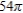
E)
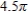

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
56
Determine the t intervals on which the curve 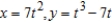 is concave downward or concave upward.
is concave downward or concave upward.
A) concave downward: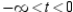 ; concave upward:
; concave upward: 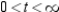
B) concave downward: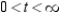 ; concave upward:
; concave upward: 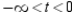
C) concave downward: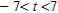 ; concave upward:
; concave upward: 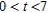
D) concave downward: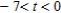 ; concave upward:
; concave upward: 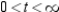
E) concave downward: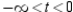 ; concave upward:
; concave upward: 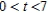
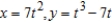 is concave downward or concave upward.
is concave downward or concave upward.A) concave downward:
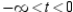 ; concave upward:
; concave upward: 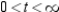
B) concave downward:
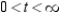 ; concave upward:
; concave upward: 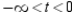
C) concave downward:
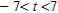 ; concave upward:
; concave upward: 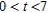
D) concave downward:
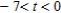 ; concave upward:
; concave upward: 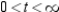
E) concave downward:
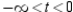 ; concave upward:
; concave upward: 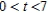

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
57
Write the corresponding rectangular equation for the curve represented by the parametric equation 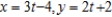 by eliminating the parameter.
by eliminating the parameter.
A)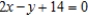
B)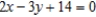
C)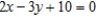
D)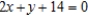
E)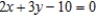
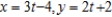 by eliminating the parameter.
by eliminating the parameter.A)
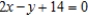
B)
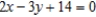
C)
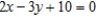
D)
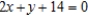
E)
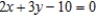

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
58
Find a set of parametric equations for the rectangular equation 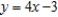 .
.
A)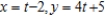
B)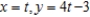
C)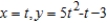
D)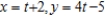
E)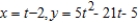
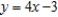 .
.A)
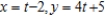
B)
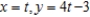
C)
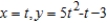
D)
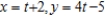
E)
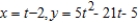

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
59
Find the area of the surface formed by revolving about the 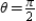 axis the following curve over the given interval.
axis the following curve over the given interval. 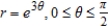
A)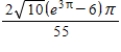
B)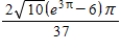
C)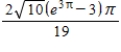
D)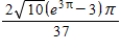
E)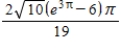
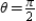 axis the following curve over the given interval.
axis the following curve over the given interval. 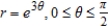
A)
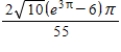
B)
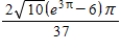
C)
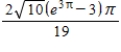
D)
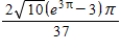
E)
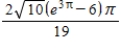

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
60
Sketch the curve represented by the parametric equations 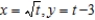 .
.
A)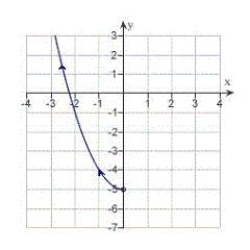
B)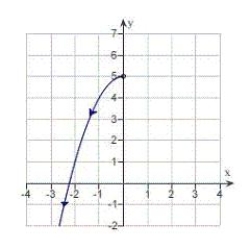
C)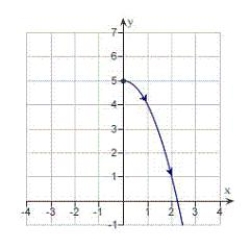
D)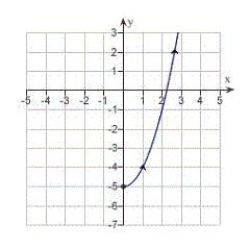
E)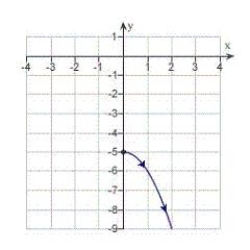
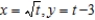 .
.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
61
Find the arc length of the curve 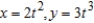 on the interval
on the interval 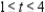 . Round your answer to three decimal places.
. Round your answer to three decimal places.
A) 287.453
B) 191.635
C) 193.606
D) 66.480
E) 99.721
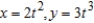 on the interval
on the interval 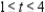 . Round your answer to three decimal places.
. Round your answer to three decimal places.A) 287.453
B) 191.635
C) 193.606
D) 66.480
E) 99.721

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
62
Find a set of parametric equations for the rectangular equation 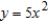 that satisfies the condition
that satisfies the condition 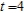 at the point
at the point 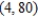 .
.
A)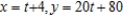
B)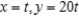
C)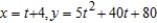
D)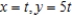
E)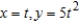
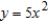 that satisfies the condition
that satisfies the condition 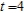 at the point
at the point 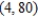 .
.A)
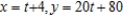
B)
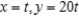
C)
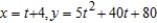
D)
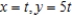
E)
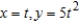

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
63
Find the area of the region lying between the loops of 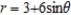 .
.
A)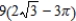
B)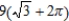
C)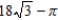
D)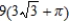
E)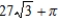
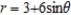 .
.A)
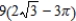
B)
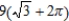
C)
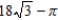
D)
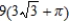
E)
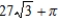

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
64
Sketch the curve represented by the parametric equations, and write the corresponding rectangular equation by eliminating the parameter. 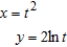
A)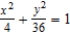
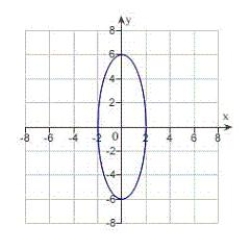
B)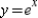
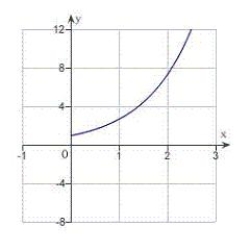
C)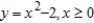
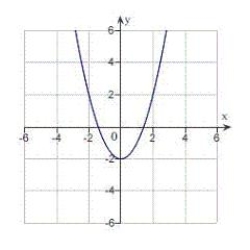
D)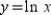
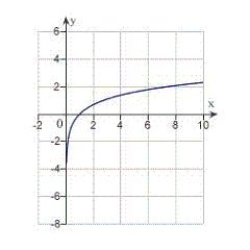
E)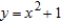
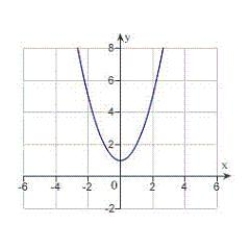
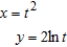
A)
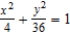

B)
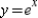

C)
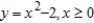

D)
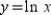

E)
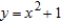


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
65
Find the area of the inner loop of 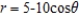 .
.
A)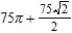
B)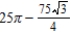
C)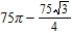
D)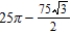
E)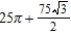
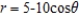 .
.A)
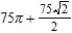
B)
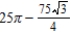
C)
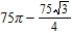
D)
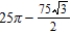
E)
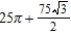

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
66
Find the area of the surface generated by revolving the curve about the given axis. 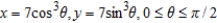 (i) x-axis; (ii) y-axis
(i) x-axis; (ii) y-axis
A)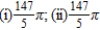
B)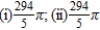
C)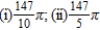
D)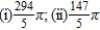
E)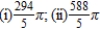
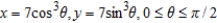 (i) x-axis; (ii) y-axis
(i) x-axis; (ii) y-axisA)
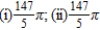
B)
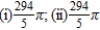
C)
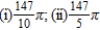
D)
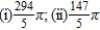
E)
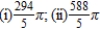

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
67
Classify the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola. 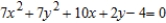
A) parabola
B) circle
C) ellipse
D) hyperbola
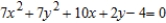
A) parabola
B) circle
C) ellipse
D) hyperbola

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
68
Find the foci of the ellipse given by 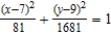 .
.
A)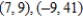
B)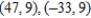
C)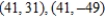
D)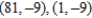
E)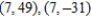
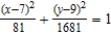 .
.A)
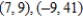
B)
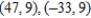
C)
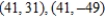
D)
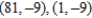
E)
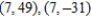

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
69
Use the result, "the set of parametric equations for the ellipse is 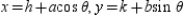 " to find a set of parametric equations for the ellipse with vertices
" to find a set of parametric equations for the ellipse with vertices 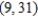 and
and 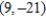 and with foci at
and with foci at 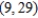 and
and 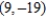 .
.
A)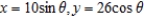
B)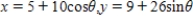
C)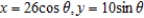
D)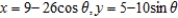
E)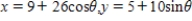
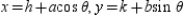 " to find a set of parametric equations for the ellipse with vertices
" to find a set of parametric equations for the ellipse with vertices 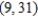 and
and 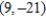 and with foci at
and with foci at 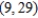 and
and 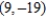 .
. A)
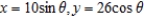
B)
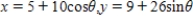
C)
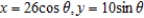
D)
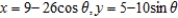
E)
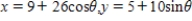

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
70
Classify the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola. 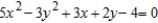
A) circle
B) hyperbola
C) ellipse
D) parabola
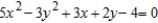
A) circle
B) hyperbola
C) ellipse
D) parabola

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
71
Identify any points at which the Folium of Descartes 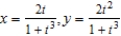 is not smooth. Round your answer to two decimal places, if necessary.
is not smooth. Round your answer to two decimal places, if necessary.
A) not smooth when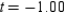
B) not smooth when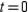
C) not smooth when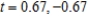
D) smooth everywhere
E) not smooth when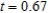
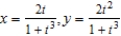 is not smooth. Round your answer to two decimal places, if necessary.
is not smooth. Round your answer to two decimal places, if necessary.A) not smooth when
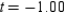
B) not smooth when
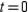
C) not smooth when
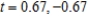
D) smooth everywhere
E) not smooth when
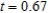

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
72
Find the distance from the pole to the directrix for the conic 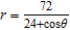 .
.
A)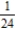
B)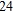
C)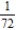
D)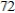
E)
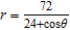 .
.A)
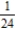
B)
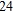
C)
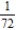
D)
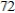
E)
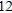

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
73
Uranus moves in an elliptical orbit with the sun at one of the foci. The length of the half of the major axis is 2,876,769,540 kilometers, and the eccentricity is 0.0444. Find the minimum distance (perihelion) of Uranus from the sun. Round your answer to nearest kilometer.
A) 3,004,498,108 km
B) 2,749,040,972 km
C) 2,819,234,149 km
D) 7,819,870,365 km
E) 2,934,304,931 km
A) 3,004,498,108 km
B) 2,749,040,972 km
C) 2,819,234,149 km
D) 7,819,870,365 km
E) 2,934,304,931 km

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
74
Find the distance from the pole to the directrix for the conic 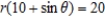 .
.
A)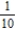
B)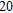
C)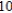
D)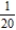
E)
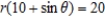 .
.A)
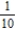
B)
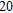
C)
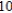
D)
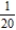
E)


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
75
Find the eccentricity of the polar equation 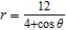 .
.
A)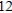
B)
C)
D)
E)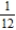
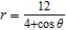 .
.A)
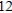
B)

C)

D)

E)

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
76
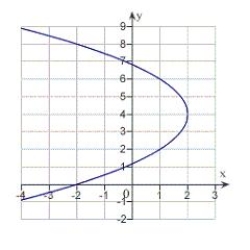
Find the vertex, focus, and directrix of the parabola and sketch its graph. 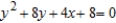
A) vertex: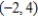 ; focus:
; focus: 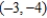 ; directrix
; directrix 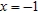
B) vertex: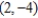 ; focus:
; focus: 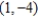 ; directrix
; directrix 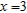
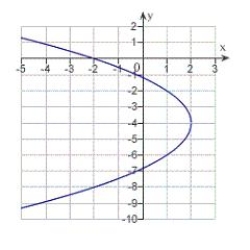
C) vertex: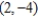 ; focus:
; focus: 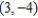 ; directrix
; directrix 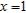
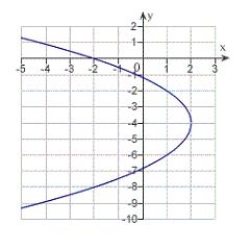
D) vertex: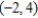 ; focus:
; focus: 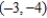 ; directrix
; directrix 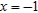
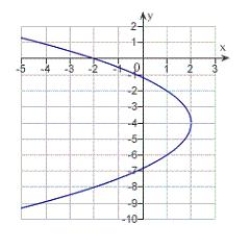
E) vertex: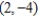 ; focus:
; focus: 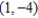 ; directrix
; directrix 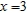
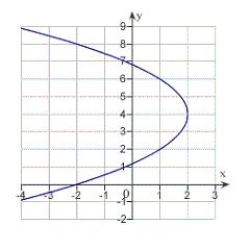
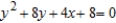
A) vertex:
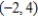 ; focus:
; focus: 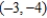 ; directrix
; directrix 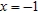

B) vertex:
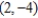 ; focus:
; focus: 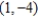 ; directrix
; directrix 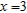

C) vertex:
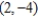 ; focus:
; focus: 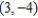 ; directrix
; directrix 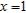

D) vertex:
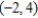 ; focus:
; focus: 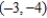 ; directrix
; directrix 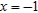

E) vertex:
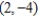 ; focus:
; focus: 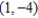 ; directrix
; directrix 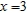


Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
77
Find the area of one petal of 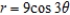 .
.
A)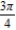
B)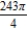
C)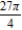
D)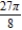
E)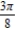
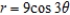 .
.A)
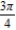
B)
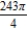
C)
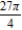
D)
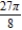
E)
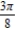

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
78
The parametric equations for the path of a projectile launched at a height h feet above the ground, at an angle  with the horizontal and having an initial velocity of
with the horizontal and having an initial velocity of  feet per second is given by
feet per second is given by 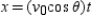 and
and 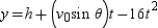 . The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of
. The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of  degrees with the horizontal at a speed of 95 miles per hour as shown in the figure. Find the minimum angle at which the ball must leave the bat in order for the hit to be a home run using the parametric equations
degrees with the horizontal at a speed of 95 miles per hour as shown in the figure. Find the minimum angle at which the ball must leave the bat in order for the hit to be a home run using the parametric equations 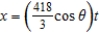 and
and 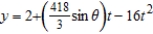 . Round your answer to one decimal place.
. Round your answer to one decimal place. 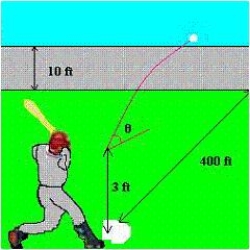
A)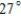
B)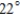
C)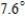
D)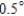
E)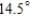
 with the horizontal and having an initial velocity of
with the horizontal and having an initial velocity of  feet per second is given by
feet per second is given by 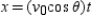 and
and 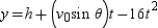 . The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of
. The center field fence in a ballpark is 10 feet high and 400 feet from home plate. The ball is hit 2 feet above the ground. It leaves the bat at an angle of  degrees with the horizontal at a speed of 95 miles per hour as shown in the figure. Find the minimum angle at which the ball must leave the bat in order for the hit to be a home run using the parametric equations
degrees with the horizontal at a speed of 95 miles per hour as shown in the figure. Find the minimum angle at which the ball must leave the bat in order for the hit to be a home run using the parametric equations 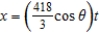 and
and 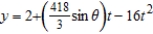 . Round your answer to one decimal place.
. Round your answer to one decimal place. 
A)
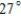
B)
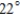
C)
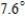
D)
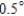
E)
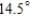

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
79
Find the area of the interior of 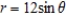 .
.
A)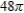
B)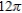
C)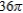
D)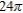
E)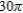
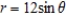 .
.A)
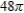
B)
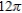
C)
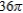
D)
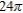
E)
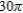

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck
80
For the given point in polar coordinates, find the corresponding rectangular coordinates for the point. 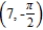 .
.
A)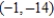
B)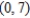
C)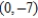
D)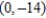
E)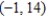
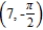 .
. A)
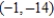
B)
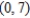
C)
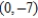
D)
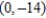
E)
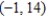

Unlock Deck
Unlock for access to all 114 flashcards in this deck.
Unlock Deck
k this deck


