Deck 9: Infinite Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/181
Play
Full screen (f)
Deck 9: Infinite Series
1
Use the Direct Comparison Test (if possible) to determine whether the series 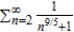
A) diverges
B) converges
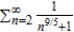
A) diverges
B) converges
B
2
Identify the graph of the first 10 terms of the sequence of partial sum of the series 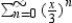 for
for 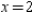 .
.
A)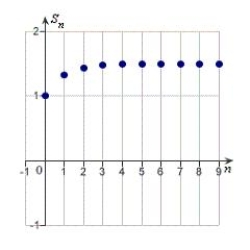
B)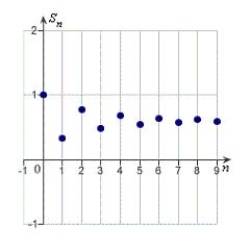
C)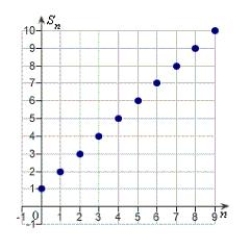
D)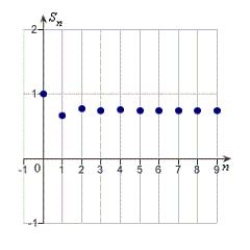
E)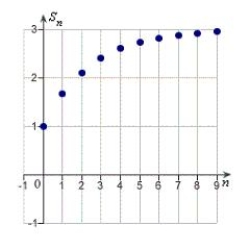
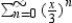 for
for 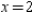 .
.A)

B)

C)

D)

E)

E
3
Find the fourth degree Maclaurin polynomial for the function. 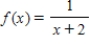
A)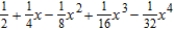
B)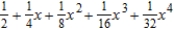
C)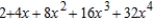
D)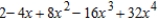
E)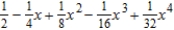
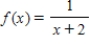
A)
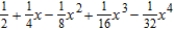
B)
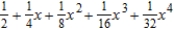
C)
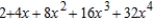
D)
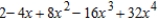
E)
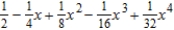
E
4
Identify the most appropriate test to be used to determine whether the series 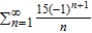 converges or diverges.
converges or diverges.
A) Ratio Test
B) ρ-Series Test
C) Alternating Series Test
D) Telescoping Series Test
E) Root Test
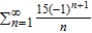 converges or diverges.
converges or diverges.A) Ratio Test
B) ρ-Series Test
C) Alternating Series Test
D) Telescoping Series Test
E) Root Test

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
5
Determine the convergence or divergence of the series using any appropriate test from this chapter. Identify the test used. 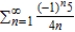
A) converges; Integral Test
B) converges; Ratio Test
C) converges; Alternating Series Test
D) diverges; Ratio Test
E) diverges; Integral Test
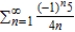
A) converges; Integral Test
B) converges; Ratio Test
C) converges; Alternating Series Test
D) diverges; Ratio Test
E) diverges; Integral Test

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
6
Use the Ratio Test to determine the convergence or divergence of the series 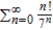 .
.
A) converges
B) diverges
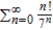 .
.A) converges
B) diverges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
7
True or false: The series 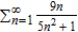 converges.
converges.
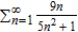 converges.
converges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
8
Find the Maclaurin polynomial of degree 5 for the function. 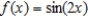
A)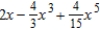
B)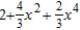
C)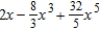
D)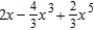
E)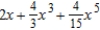
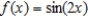
A)
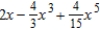
B)
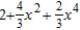
C)
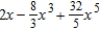
D)
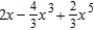
E)
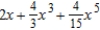

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
9
Determine the convergence or divergence of the series using any appropriate test from this chapter. Identify the test used. 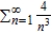
A) diverges; Ratio Test
B) converges; both p-series and Integral Test
C) converges; p-series
D) converges; Integral Test
E) diverges; p-series
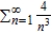
A) diverges; Ratio Test
B) converges; both p-series and Integral Test
C) converges; p-series
D) converges; Integral Test
E) diverges; p-series

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
10
Use a graphing utility to graph 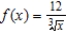 and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at
and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at 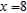 .
.
A) 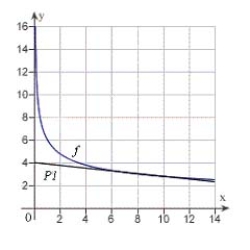
B) 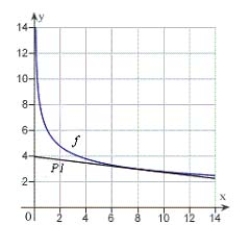
C) 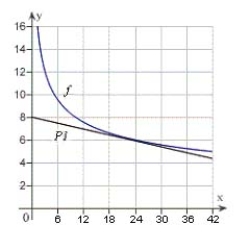
D) 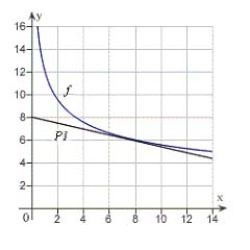
E) 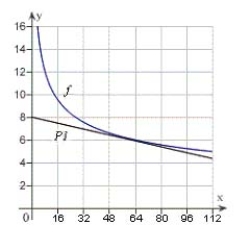
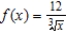 and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at
and P1, a first-degree polynomial function whose value and slope agree with the value and slope of f at 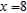 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
11
Use the Direct Comparison Test to determine the convergence or divergence of the series 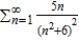 .
.
A) The series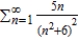 diverges.
diverges.
B) The series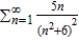 converges.
converges.
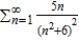 .
.A) The series
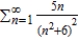 diverges.
diverges.B) The series
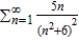 converges.
converges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
12
Match the sequence with its graph. 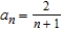
A)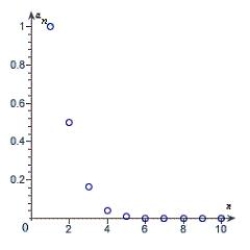
B)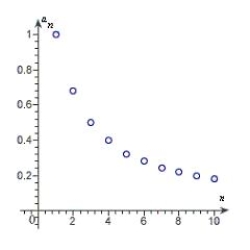
C)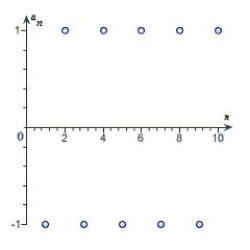
D)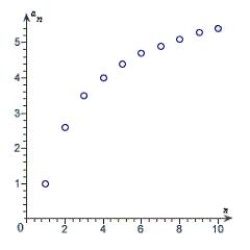
E)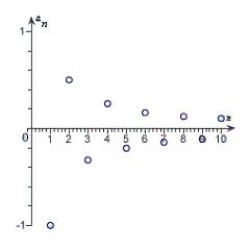
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
13
Approximate the sum of the series by using the first six terms. 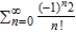
A) 0.723 < S < 0.743
B) 0.683 < S < 0.763
C) 0.733 < S < 0.738
D) 0.693 < S < 0.733
E) 0.73 < S < 0.736
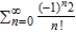
A) 0.723 < S < 0.743
B) 0.683 < S < 0.763
C) 0.733 < S < 0.738
D) 0.693 < S < 0.733
E) 0.73 < S < 0.736

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
14
Match the sequence with its graph. 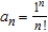
A)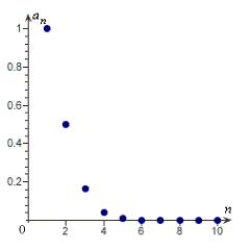
B)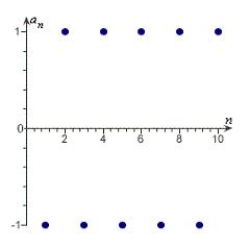
C)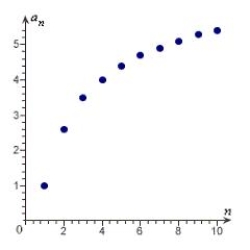
D)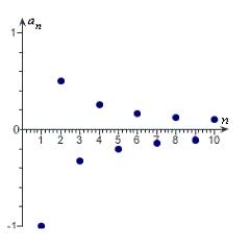
E)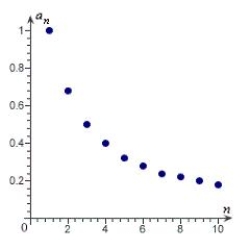
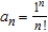
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
15
Match the sequence with its graph. 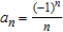
A)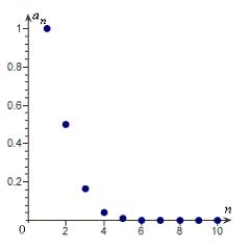
B)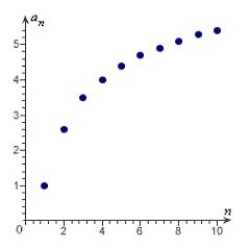
C)
D)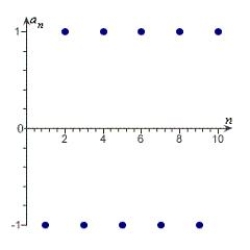
E)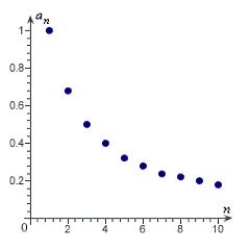
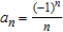
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
16
Use the definition to find the Taylor series centered at 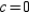 for the function
for the function 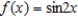 .
.
A)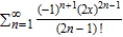
B)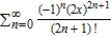
C)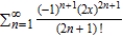
D)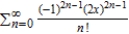
E)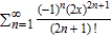
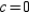 for the function
for the function 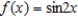 .
.A)
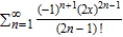
B)
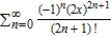
C)
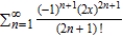
D)
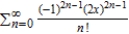
E)
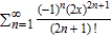

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
17
Find all values of x for which the series converges. For these values of x, write the sum of the series as a function of x. 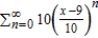
A)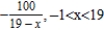
B)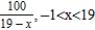
C)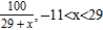
D)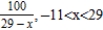
E) The series diverges for all x.
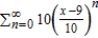
A)
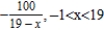
B)
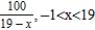
C)
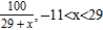
D)
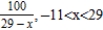
E) The series diverges for all x.

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
18
Use the Root Test to determine the convergence or divergence of the series. 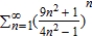
A) Root Test inconclusive
B) diverges
C) converges
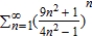
A) Root Test inconclusive
B) diverges
C) converges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
19
True or false. The series 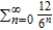 is convergent.
is convergent.
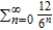 is convergent.
is convergent.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
20
Write the first three terms of the sequence. 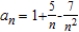
A)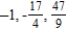
B)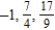
C)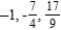
D)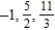
E)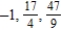
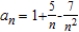
A)
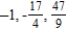
B)
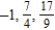
C)
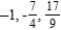
D)
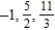
E)
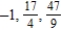

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
21
Find the Maclaurin polynomial of degree 3 for the function. 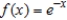
A)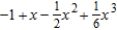
B)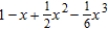
C)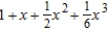
D)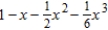
E)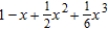
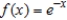
A)
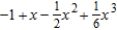
B)
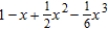
C)
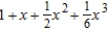
D)
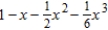
E)
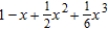

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
22
Determine the convergence or divergence of the sequence with the given nth term. If the sequence converges, find its limit. 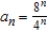
A) The sequence converges to 0.
B) The sequence diverges to -2.
C) The sequence converges to 1.
D) The sequence converges to -1.
E) The sequence diverges.
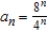
A) The sequence converges to 0.
B) The sequence diverges to -2.
C) The sequence converges to 1.
D) The sequence converges to -1.
E) The sequence diverges.

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
23
Find a power series for the function 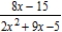 centered at 0.
centered at 0.
A)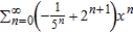
B)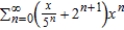
C)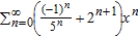
D)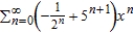
E)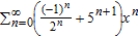
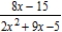 centered at 0.
centered at 0.A)
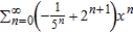
B)
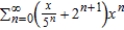
C)
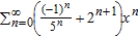
D)
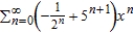
E)
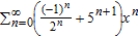

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
24
Find the Maclaurin polynomial of degree 4 for the function. 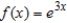
A)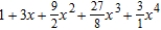
B)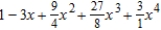
C)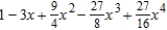
D)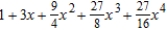
E)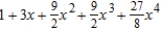
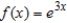
A)
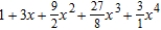
B)
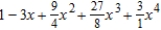
C)
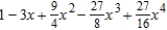
D)
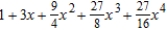
E)
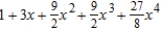

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
25
Approximate the sum of the series by using the first six terms. 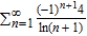
A) 0.783 < S < 4.630
B) 2.066 < S < 3.348
C) 1.745 < S < 3.669
D) 0.569 < S < 4.844
E) 0.302 < S < 5.111
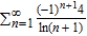
A) 0.783 < S < 4.630
B) 2.066 < S < 3.348
C) 1.745 < S < 3.669
D) 0.569 < S < 4.844
E) 0.302 < S < 5.111

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
26
Write the first five terms of the sequence of partial sums. 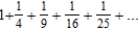
A)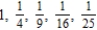
B)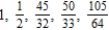
C)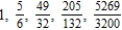
D)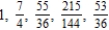
E)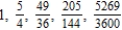
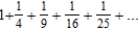
A)
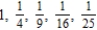
B)
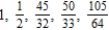
C)
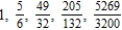
D)
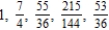
E)
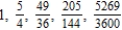

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
27
Determine the convergence or divergence of the series. 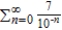
A) cannot be determined from the methods in the chapter
B) Diverges
C) Converges
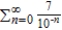
A) cannot be determined from the methods in the chapter
B) Diverges
C) Converges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the function given by 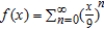 . Find the interval of convergence for
. Find the interval of convergence for 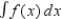 .
.
A)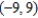
B)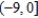
C)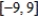
D)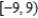
E)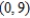
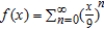 . Find the interval of convergence for
. Find the interval of convergence for 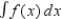 .
.A)
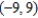
B)
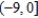
C)
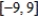
D)
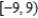
E)
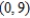

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
29
If the rate of inflation is 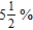 per year and the average price of a car is currently $35,000, the average price after n years is
per year and the average price of a car is currently $35,000, the average price after n years is 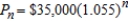 . Compute the average price after 8 years. Round your answer to two decimal places.
. Compute the average price after 8 years. Round your answer to two decimal places.
A) $22,259.86
B) $53,714.03
C) $295,400.00
D) $46,685.40
E) $264,600.00
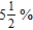 per year and the average price of a car is currently $35,000, the average price after n years is
per year and the average price of a car is currently $35,000, the average price after n years is 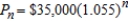 . Compute the average price after 8 years. Round your answer to two decimal places.
. Compute the average price after 8 years. Round your answer to two decimal places.A) $22,259.86
B) $53,714.03
C) $295,400.00
D) $46,685.40
E) $264,600.00

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
30
Use the polynomial test to determine whether the series 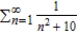 converges or diverges.
converges or diverges.
A) The series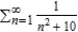 converges.
converges.
B) The series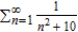 diverges.
diverges.
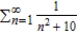 converges or diverges.
converges or diverges.A) The series
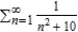 converges.
converges.B) The series
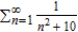 diverges.
diverges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
31
A government program that currently costs taxpayers $3.5 billion per year is cut back by 40 percent per year. Compute the budget after the fourth year. Round your answer to the nearest integer.
A) $1,433,600,000
B) $165,995,062
C) $89,600,000
D) $1,012,217,284
E) $453,600,000
A) $1,433,600,000
B) $165,995,062
C) $89,600,000
D) $1,012,217,284
E) $453,600,000

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
32
Determine the convergence or divergence of the series. 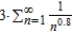
A) diverges
B) converges
C) cannot be determined
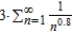
A) diverges
B) converges
C) cannot be determined

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
33
Determine whether the series 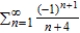 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
A) The series converges conditionally but does not converge absolutely.
B) The series converges absolutely but does not converge conditionally.
C) The series diverges.
D) The series converges absolutely.
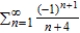 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.A) The series converges conditionally but does not converge absolutely.
B) The series converges absolutely but does not converge conditionally.
C) The series diverges.
D) The series converges absolutely.

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the sequence 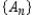 whose nth term is given by
whose nth term is given by 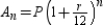 where P is the principal,
where P is the principal, 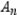 is the account balance in dollars after n months, and r is the interest rate compounded annually. Find the sixth term of the sequence if
is the account balance in dollars after n months, and r is the interest rate compounded annually. Find the sixth term of the sequence if 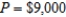 and
and 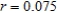 . Round your answer to two decimal places.
. Round your answer to two decimal places.
A) $9,518.26
B) $10,061.16
C) $9,696.45
D) $9,342.82
E) $9,412.67
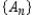 whose nth term is given by
whose nth term is given by 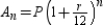 where P is the principal,
where P is the principal, 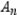 is the account balance in dollars after n months, and r is the interest rate compounded annually. Find the sixth term of the sequence if
is the account balance in dollars after n months, and r is the interest rate compounded annually. Find the sixth term of the sequence if 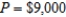 and
and 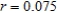 . Round your answer to two decimal places.
. Round your answer to two decimal places. A) $9,518.26
B) $10,061.16
C) $9,696.45
D) $9,342.82
E) $9,412.67

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
35
Determine whether the series 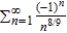 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.
A) converges conditionally
B) diverges
C) converges absolutely
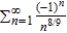 converges absolutely, converges conditionally, or diverges.
converges absolutely, converges conditionally, or diverges.A) converges conditionally
B) diverges
C) converges absolutely

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose the winner of a $10,000,000 sweepstakes will be paid $200,000 per year for 50 years, starting a year from now. The money earns 6% interest per year. The present value of the winnings is 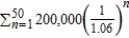 Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
A) $10,542,883.62
B) $3,323,509.25
C) $7,028,589.08
D) $2,556,671.23
E) $3,152,372.13
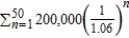 Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.
Compute the present value using the formula for the nth partial sum of a geometric series. Round your answer to two decimal places.A) $10,542,883.62
B) $3,323,509.25
C) $7,028,589.08
D) $2,556,671.23
E) $3,152,372.13

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
37
Identify the interval of convergence of a power series 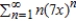 .
.
A)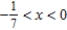
B)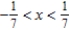
C)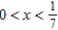
D)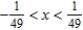
E)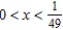
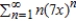 .
.A)
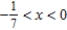
B)
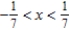
C)
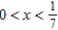
D)
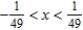
E)
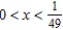

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
38
Use the Ratio Test to determine the convergence or divergence of the series 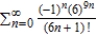 .
.
A) diverges
B) converges
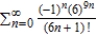 .
.A) diverges
B) converges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
39
Approximate the sum of the series by using the first six terms. 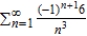
A) 5.398 < S < 5.404
B) 5.393 < S < 5.405
C) 5.381 < S < 5.416
D) 5.391 < S < 5.391
E) 5.297 < S < 5.501
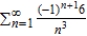
A) 5.398 < S < 5.404
B) 5.393 < S < 5.405
C) 5.381 < S < 5.416
D) 5.391 < S < 5.391
E) 5.297 < S < 5.501

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
40
Use a power series to approximate the value of the integral 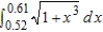 with an error less than 0.001. Round your answer to four decimal places.
with an error less than 0.001. Round your answer to four decimal places.
A) 0.1063
B) 0.0900
C) 0.0982
D) 0.1071
E) 0.0985
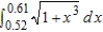 with an error less than 0.001. Round your answer to four decimal places.
with an error less than 0.001. Round your answer to four decimal places.A) 0.1063
B) 0.0900
C) 0.0982
D) 0.1071
E) 0.0985

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
41
Write the next two apparent terms of the sequence 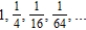 .
.
A)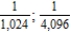
B)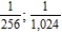
C)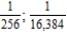
D)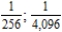
E)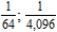
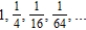 .
.A)
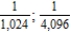
B)
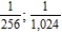
C)
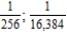
D)
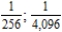
E)
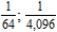

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
42
Suppose the annual spending by tourists in a resort city is $100 million. Approximately 75% of that revenue is again spent in the resort city, and of that amount approximately 75% is again spent in the same city, and so on. Summing all of this spending indefinitely, leads to the geometric series 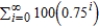 . Find the sum of this series.
. Find the sum of this series.
A) $800 million
B) $401 million
C) $200 million
D) $801 million
E) $400 million
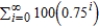 . Find the sum of this series.
. Find the sum of this series.A) $800 million
B) $401 million
C) $200 million
D) $801 million
E) $400 million

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
43
Write the first five terms of the sequence of partial sums. 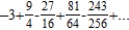
A)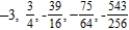
B)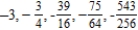
C)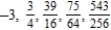
D)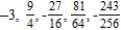
E)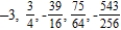
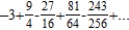
A)
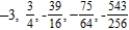
B)
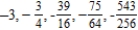
C)
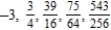
D)
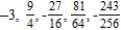
E)
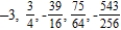

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
44
True or false: The series 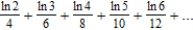 converges.
converges.
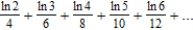 converges.
converges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
45
Sketch the graph of the sequence of partial sum of the series 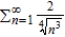 .
.
A)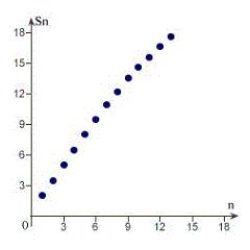
B)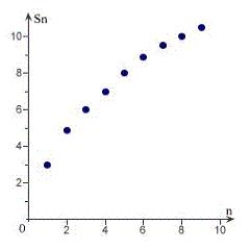
C)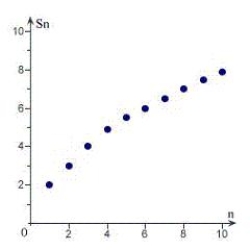
D)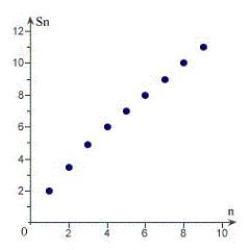
E)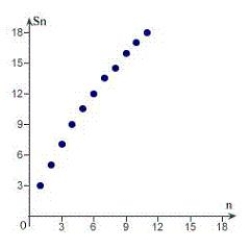
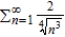 .
. A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
46
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of 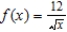 at
at 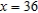 .
.
A)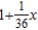
B)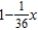
C)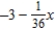
D)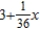
E)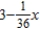
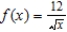 at
at 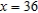 .
.A)
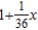
B)
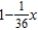
C)
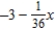
D)
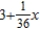
E)
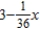

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
47
Use the Limit Comparison Test to determine the convergence or divergence of the series 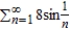 .
.
A) The series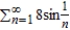 converges.
converges.
B) The series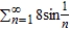 diverges.
diverges.
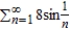 .
.A) The series
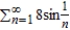 converges.
converges.B) The series
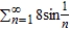 diverges.
diverges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
48
Determine the minimal number of terms required to approximate the sum of the series with an error of less than 0.007. 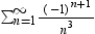
A) 5
B) 4
C) 2
D) 6
E) 3
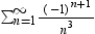
A) 5
B) 4
C) 2
D) 6
E) 3

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
49
Find the sum of the convergent series. 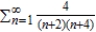
A)
B)
C)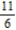
D)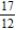
E)
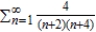
A)

B)

C)
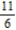
D)
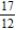
E)


Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
50
Use the binomial series to find the Maclaurian series for the function. 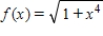
A) 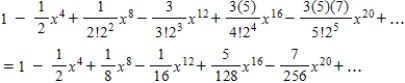
B) 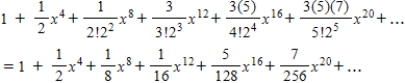
C) 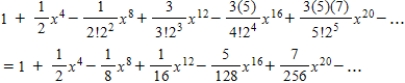
D) 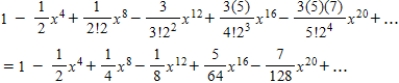
E) 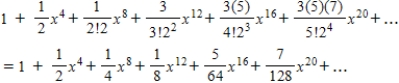
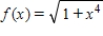
A)
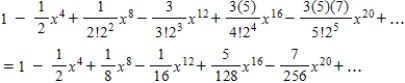
B)
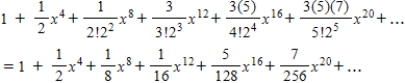
C)
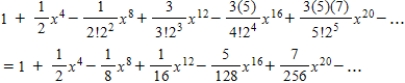
D)
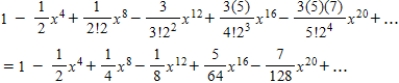
E)
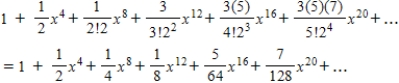

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
51
Use the Limit Comparison Test (if possible) to determine whether the series 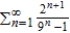 converges or diverges.
converges or diverges.
A) diverges
B) converges
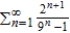 converges or diverges.
converges or diverges. A) diverges
B) converges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
52
Find the interval of convergence of the power series. (Be sure to include a check for convergence at the endpoints of the interval.) 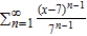
A)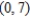
B)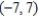
C)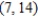
D)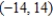
E)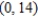
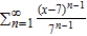
A)
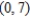
B)
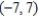
C)
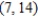
D)
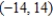
E)
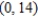

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
53
Find the interval of convergence of the power series 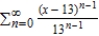 . (Be sure to include a check for convergence at the endpoints of the interval.)
. (Be sure to include a check for convergence at the endpoints of the interval.)
A)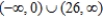
B)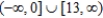
C)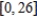
D)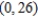
E)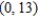
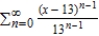 . (Be sure to include a check for convergence at the endpoints of the interval.)
. (Be sure to include a check for convergence at the endpoints of the interval.)A)
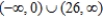
B)
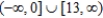
C)
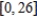
D)
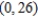
E)
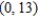

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
54
Find the fourth degree Taylor polynomial centered at 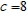 for the function.
for the function. 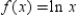
A)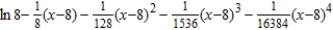
B)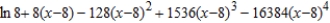
C)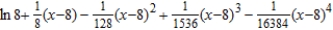
D)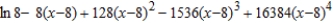
E)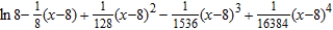
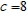 for the function.
for the function. 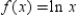
A)
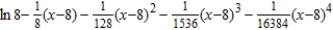
B)
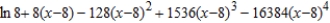
C)
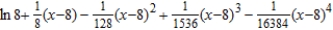
D)
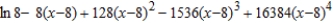
E)
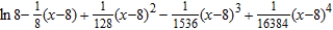

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
55
Use the polynomial test to determine whether the series 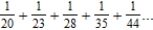 converges or diverges.
converges or diverges.
A) The series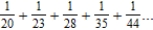 diverges.
diverges.
B) The series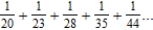 converges.
converges.
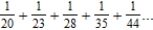 converges or diverges.
converges or diverges.A) The series
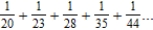 diverges.
diverges.B) The series
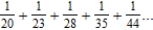 converges.
converges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
56
Use a power series to approximate the value of the integral 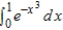 with an error of less than 0.01. Round your answer to two decimal places.
with an error of less than 0.01. Round your answer to two decimal places.
A) 0.74
B) 0.89
C) 0.88
D) 0.84
E) 0.81
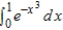 with an error of less than 0.01. Round your answer to two decimal places.
with an error of less than 0.01. Round your answer to two decimal places. A) 0.74
B) 0.89
C) 0.88
D) 0.84
E) 0.81

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose an electronic games manufacturer producing a new product estimates the annual sales to be 7,000 units. Each year 25% of the units that have been sold will become inoperative. So, 7,000 units will be in use after 1 year, 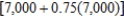 units will be in use after 2 years, and so on. How many units will be in use after n years?
units will be in use after 2 years, and so on. How many units will be in use after n years?
A)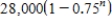 units
units
B)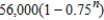 units
units
C)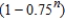 units
units
D)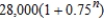 units
units
E)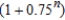 units
units
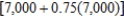 units will be in use after 2 years, and so on. How many units will be in use after n years?
units will be in use after 2 years, and so on. How many units will be in use after n years? A)
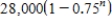 units
unitsB)
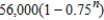 units
unitsC)
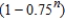 units
unitsD)
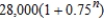 units
unitsE)
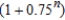 units
units
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
58
Use the Integral Test to determine the convergence or divergence of the series. 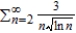
A) diverges
B) converges
C) Integral Test inconclusive
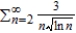
A) diverges
B) converges
C) Integral Test inconclusive

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
59
Use the power series 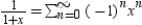 to determine a power series centered at 0 for the function
to determine a power series centered at 0 for the function 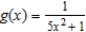 . .
. .
A)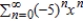
B)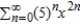
C)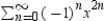
D)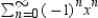
E)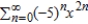
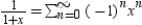 to determine a power series centered at 0 for the function
to determine a power series centered at 0 for the function 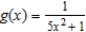 . .
. .A)
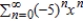
B)
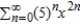
C)
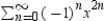
D)
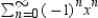
E)
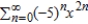

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
60
State where the power series 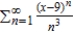 is centered.
is centered.
A) 0
B) -3
C) 9
D) 3
E) -9
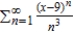 is centered.
is centered.A) 0
B) -3
C) 9
D) 3
E) -9

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose you go to work at a company that pays $0.02 for the first day, $0.04 for the second day, $0.08 for the third day, and so on. If the daily wage keeps doubling, what would your total income be for working 29 days? Round your answer to two decimal places.
A) $5,368,709.12
B) $2,684,354.56
C) $10,737,418.22
D) $42,949,672.88
E) $21,474,836.44
A) $5,368,709.12
B) $2,684,354.56
C) $10,737,418.22
D) $42,949,672.88
E) $21,474,836.44

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
62
Use the Direct Comparison Test (if possible) to determine whether the series 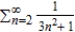 converges or diverges.
converges or diverges.
A) converges
B) diverges
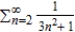 converges or diverges.
converges or diverges. A) converges
B) diverges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
63
Use the binomial series to find the Maclaurian series for the function 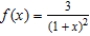 .
.
A)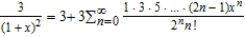
B)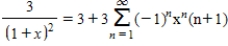
C)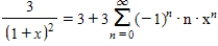
D)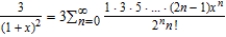
E)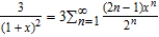
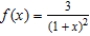 .
. A)
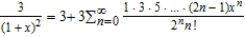
B)
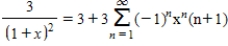
C)
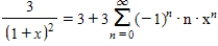
D)
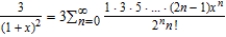
E)
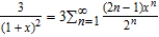

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
64
Explain how to use the geometric series 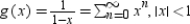 to find the series for the function
to find the series for the function 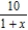 .
.
A) replace x with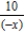
B) replace x with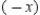 and multiply the series by
and multiply the series by 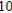
C) replace x with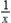 and divide the series by
and divide the series by 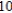
D) replace x with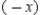 and divide the series by
and divide the series by 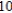
E) replace x with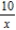
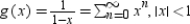 to find the series for the function
to find the series for the function 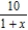 .
.A) replace x with
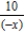
B) replace x with
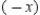 and multiply the series by
and multiply the series by 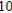
C) replace x with
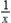 and divide the series by
and divide the series by 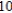
D) replace x with
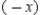 and divide the series by
and divide the series by 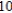
E) replace x with
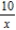

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
65
Find the Maclaurin series for the function 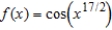 .
.
A)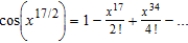
B)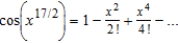
C)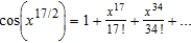
D)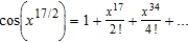
E)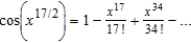
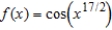 .
.A)
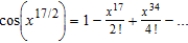
B)
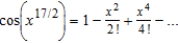
C)
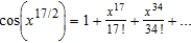
D)
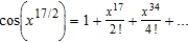
E)
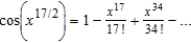

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
66
Determine whether the series 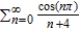 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.
A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.
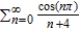 converges conditionally or absolutely, or diverges.
converges conditionally or absolutely, or diverges.A) The series converges absolutely.
B) The series diverges.
C) The series converges absolutely but does not converge conditionally.
D) The series converges conditionally but does not converge absolutely.

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
67
Find the Maclaurin polynomial of degree 4 for the function. 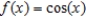
A)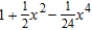
B)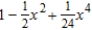
C)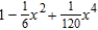
D)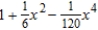
E)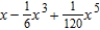
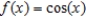
A)
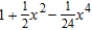
B)
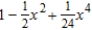
C)
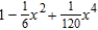
D)
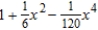
E)
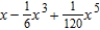

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
68
Find the radius of convergence of the power series. 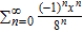
A)
B)
C) 8
D)
E) 64
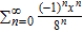
A)

B)

C) 8
D)

E) 64

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
69
Use the definition to find the Taylor series centered at 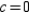 for the function
for the function 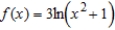 .
.
A)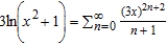
B)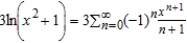
C)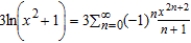
D)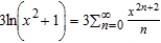
E)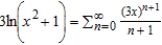
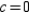 for the function
for the function 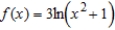 .
.A)
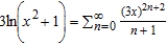
B)
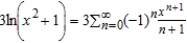
C)
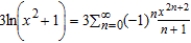
D)
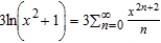
E)
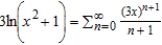

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
70
Use the power series 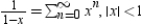 to determine a power series for the function
to determine a power series for the function 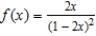 .
.
A)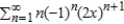
B)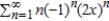
C)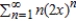
D)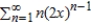
E)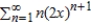
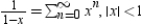 to determine a power series for the function
to determine a power series for the function 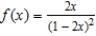 .
.A)
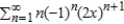
B)
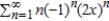
C)
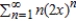
D)
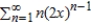
E)
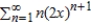

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
71
Use the Direct Comparison Test to determine the convergence or divergence of the series 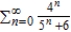 .
.
A) The series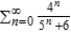 converges.
converges.
B) The series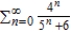 diverges.
diverges.
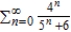 .
.A) The series
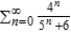 converges.
converges.B) The series
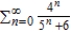 diverges.
diverges.
Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
72
Determine the values of x for which the function 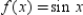 can be replaced by the Taylor polynomial
can be replaced by the Taylor polynomial 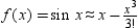 if the error cannot exceed 0.006. Round your answer to four decimal places.
if the error cannot exceed 0.006. Round your answer to four decimal places.
A)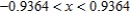
B)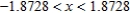
C)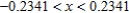
D)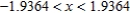
E)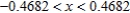
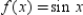 can be replaced by the Taylor polynomial
can be replaced by the Taylor polynomial 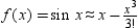 if the error cannot exceed 0.006. Round your answer to four decimal places.
if the error cannot exceed 0.006. Round your answer to four decimal places.A)
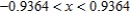
B)
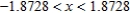
C)
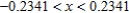
D)
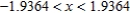
E)
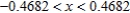

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
73
Find a geometric power series for the function 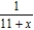 centered at 0.
centered at 0.
A)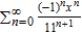
B)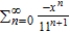
C)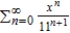
D)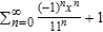
E)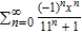
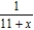 centered at 0.
centered at 0.A)
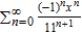
B)
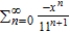
C)
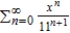
D)
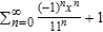
E)
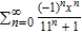

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
74
Find the sum of the convergent series 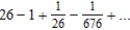
A)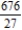
B)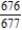
C)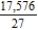
D)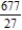
E)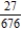
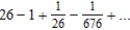
A)
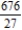
B)
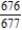
C)
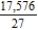
D)
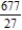
E)
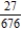

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
75
Use Theorem 9.11 to determine the convergence or divergence of the series. 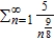
A) diverges
B) converges
C) Theorem 9.11 inconclusive
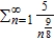
A) diverges
B) converges
C) Theorem 9.11 inconclusive

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
76
Find a first-degree polynomial function P1 whose value and slope agree with the value and slope of f at  . What is P1 called?
. What is P1 called? 
A)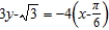 ; tangent line to
; tangent line to 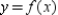 at
at 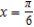
B)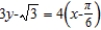 ; secant line to
; secant line to 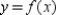 at
at 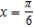
C)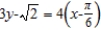 ; tangent line to
; tangent line to 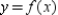 at
at 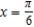
D)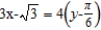 ; differential of
; differential of 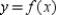 at
at 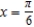
E)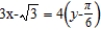 ; tangent line to
; tangent line to 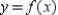 at
at 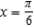
 . What is P1 called?
. What is P1 called? 
A)
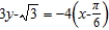 ; tangent line to
; tangent line to 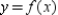 at
at 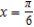
B)
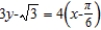 ; secant line to
; secant line to 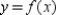 at
at 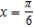
C)
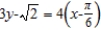 ; tangent line to
; tangent line to 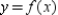 at
at 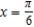
D)
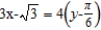 ; differential of
; differential of 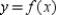 at
at 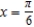
E)
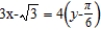 ; tangent line to
; tangent line to 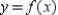 at
at 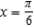

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
77
Use the Ratio Test to determine the convergence or divergence of the series. 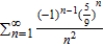
A) converges
B) Ratio Test inconclusive
C) diverges
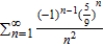
A) converges
B) Ratio Test inconclusive
C) diverges

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
78
The terms of a series 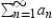 are defined recursively. Determine the convergence or divergence of the series. Explain your reasoning.
are defined recursively. Determine the convergence or divergence of the series. Explain your reasoning. 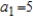 ,
, 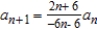
A) diverges; Ratio Test
B) converges; Ratio Test
C) converges; Integral Test
D) diverges; Alternating Series Test
E) diverges; Root Test
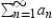 are defined recursively. Determine the convergence or divergence of the series. Explain your reasoning.
are defined recursively. Determine the convergence or divergence of the series. Explain your reasoning. 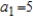 ,
, 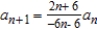
A) diverges; Ratio Test
B) converges; Ratio Test
C) converges; Integral Test
D) diverges; Alternating Series Test
E) diverges; Root Test

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
79
Identify the interval of convergence of a power series 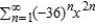 .
.
A)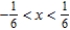
B)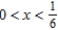
C)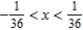
D)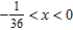
E)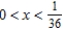
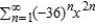 .
.A)
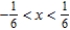
B)
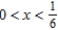
C)
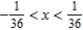
D)
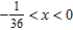
E)
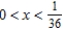

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck
80
Find a power series for the function 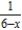 centered at 1.
centered at 1.
A)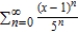
B)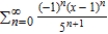
C)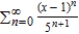
D)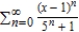
E)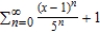
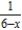 centered at 1.
centered at 1.A)
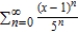
B)
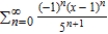
C)
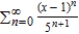
D)
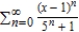
E)
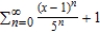

Unlock Deck
Unlock for access to all 181 flashcards in this deck.
Unlock Deck
k this deck


