Deck 6: Transportation, Transshipment, and Assignment Problems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/80
Play
Full screen (f)
Deck 6: Transportation, Transshipment, and Assignment Problems
1
A transportation problem involves the following costs, supply, and demand:
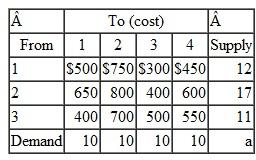 Solve this problem by using the computer.
Solve this problem by using the computer.
 Solve this problem by using the computer.
Solve this problem by using the computer.First, put together the linear programming model; where the destinations are represented with the numbers 1-4 and the sources are 1-3. For this problem, we will use A, B, C and D to represent the destinations.
Consider the following table:
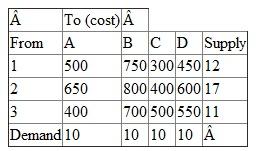 Maximize
Maximize
 This would be subject to the following equations
This would be subject to the following equations
 Representing the supply
Representing the supply
 Representing the demand
Representing the demand
Where,
 Now, to solve this transportation problem, use the QM for Window software (provided with the book) following these instructions:
Now, to solve this transportation problem, use the QM for Window software (provided with the book) following these instructions:
First, open the software; under module, select Transportation. Next, open a blank document.
A menu will open; enter the document title if needed. Then, enter the number of Sources (1, 2 and 3) which is 3 for this problem.
Enter the number of destinations which is 4 for this problem ( A, B, C and D ).
Select OK and a window will show in order to enter the equations.
Enter the values for Destination and Sources; and enter the given supply and demand numbers (3 and 4 for this problem); then, select solve on the top right corner and a series of windows with solutions.
The window titled: Transportation Shipments has the values of the variables.
From source 1 to destination C the value is 2
From source 1 to destination D the value is 10
From source 2 to destination B the value is 9
From source 2 to destination C the value is 8
From source 3 to destination A the value is 10
From source 3 to destination B the value is 1
From source 1 to destination A the value is 0
Hence,

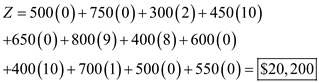
Consider the following table:
 Maximize
Maximize  This would be subject to the following equations
This would be subject to the following equations Representing the supply
Representing the supply Representing the demand
Representing the demandWhere,
 Now, to solve this transportation problem, use the QM for Window software (provided with the book) following these instructions:
Now, to solve this transportation problem, use the QM for Window software (provided with the book) following these instructions:First, open the software; under module, select Transportation. Next, open a blank document.
A menu will open; enter the document title if needed. Then, enter the number of Sources (1, 2 and 3) which is 3 for this problem.
Enter the number of destinations which is 4 for this problem ( A, B, C and D ).
Select OK and a window will show in order to enter the equations.
Enter the values for Destination and Sources; and enter the given supply and demand numbers (3 and 4 for this problem); then, select solve on the top right corner and a series of windows with solutions.
The window titled: Transportation Shipments has the values of the variables.
From source 1 to destination C the value is 2
From source 1 to destination D the value is 10
From source 2 to destination B the value is 9
From source 2 to destination C the value is 8
From source 3 to destination A the value is 10
From source 3 to destination B the value is 1
From source 1 to destination A the value is 0
Hence,

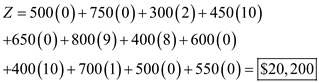
2
The Shotz Beer Company has breweries in two cities; the breweries can supply the following numbers of barrels of draft beer to the company's distributors each month:
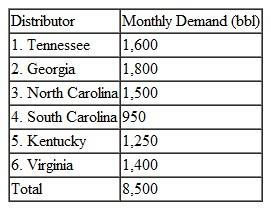
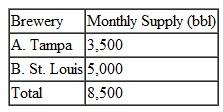 The distributors, which are spread throughout six states, have the following total monthly demand:
The distributors, which are spread throughout six states, have the following total monthly demand:
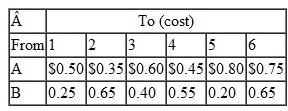
 The company must pay the following shipping costs per barrel:
The company must pay the following shipping costs per barrel:
 Solve this problem by using the computer.
Solve this problem by using the computer.
 The distributors, which are spread throughout six states, have the following total monthly demand:
The distributors, which are spread throughout six states, have the following total monthly demand: The company must pay the following shipping costs per barrel:
The company must pay the following shipping costs per barrel: Solve this problem by using the computer.
Solve this problem by using the computer.Put together the linear programming model where the destinations are represented with the numbers 1-6 and the sources are represented with A and B.
Maximize
 This would subject to the following equations
This would subject to the following equations
 Representing the supply
Representing the supply
 Representing the demand
Representing the demand
Where,
 To solve this transportation problem, use the QM for Window software as follows:
To solve this transportation problem, use the QM for Window software as follows:
First, open the software under module, select Transportation.
Next, open a blank document. A menu will open; enter the document title if needed. Then, enter the number of Sources (A and B) for the problem.
Enter the number of destinations which is 6 for this problem ( 1-6 ).
Select OK and a window will show in order to enter the equations.
Enter the values for Destination and Sources. Thereafter, enter the given supply and demand numbers.
Then, select solve on the top right corner and a series of windows with solutions. The window titled: Transportation Shipments has the values of the variables.
From source A to destination 2 the value is 1800
From source A to destination 4 the value is 950
From source A to destination 6 the value is 750
From source B to destination 1 the value is 1600
From source B to destination 3 the value is 1500
From source B to destination 5 the value is 1250
From source B to destination 6 the value is 650
Hence,

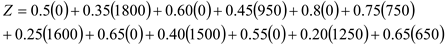 Z = 3,292.50
Z = 3,292.50
Total transportation cost for the company is $ 3292.50
Maximize
 This would subject to the following equations
This would subject to the following equations Representing the supply
Representing the supply Representing the demand
Representing the demandWhere,
 To solve this transportation problem, use the QM for Window software as follows:
To solve this transportation problem, use the QM for Window software as follows:First, open the software under module, select Transportation.
Next, open a blank document. A menu will open; enter the document title if needed. Then, enter the number of Sources (A and B) for the problem.
Enter the number of destinations which is 6 for this problem ( 1-6 ).
Select OK and a window will show in order to enter the equations.
Enter the values for Destination and Sources. Thereafter, enter the given supply and demand numbers.
Then, select solve on the top right corner and a series of windows with solutions. The window titled: Transportation Shipments has the values of the variables.
From source A to destination 2 the value is 1800
From source A to destination 4 the value is 950
From source A to destination 6 the value is 750
From source B to destination 1 the value is 1600
From source B to destination 3 the value is 1500
From source B to destination 5 the value is 1250
From source B to destination 6 the value is 650
Hence,

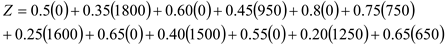 Z = 3,292.50
Z = 3,292.50Total transportation cost for the company is $ 3292.50
3
Suntrek in Problem ships the cotton it has purchased from the U.S. ports to overseas ports in Shanghai, Karachi, and Saigon, where its denim fabric factories are also located. The shipping and handling costs per bale of cotton from each U.S. port to each of Suntrek's overseas factories and the demand at these factories are as follows:
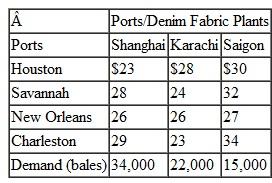 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.
Problem
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
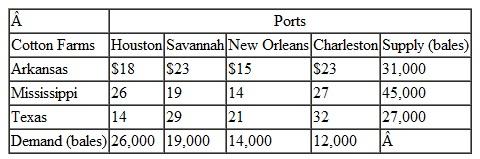 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.Problem
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.Consider the Ports as H, S, N, and C and Denim fabric plant as 1,2 and 3.
Therefore,
Objective function:
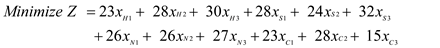 Subject to constraints:
Subject to constraints:
Supply constraints H, S, N and C will be as shown below :
 Demand constraints at 1, 2, and 3 will be as shown below:
Demand constraints at 1, 2, and 3 will be as shown below:
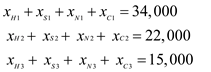 Non -negative Constraints
Non -negative Constraints
 Formulate the problem as shown below:
Formulate the problem as shown below:
Step 1 Enter the values of different variables, constraints and objective in Excel and use the formulas as shown below:
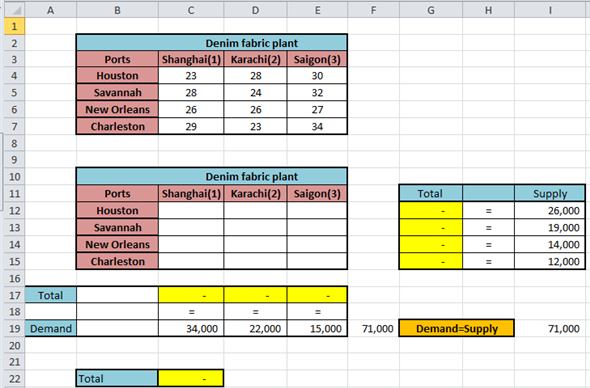 Step 2 Use the formulas for each row and column as shown below:
Step 2 Use the formulas for each row and column as shown below:
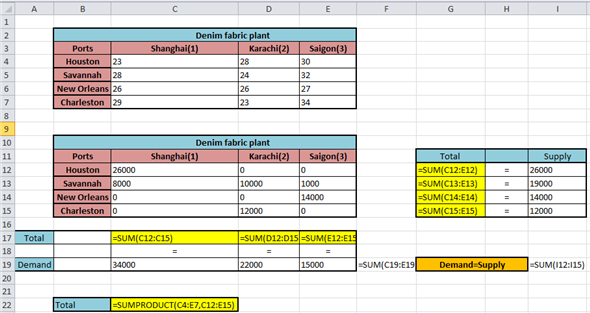 Step 3 Enter the value of the variables, constraints and objective function in Excel Solver, as shown below:
Step 3 Enter the value of the variables, constraints and objective function in Excel Solver, as shown below:
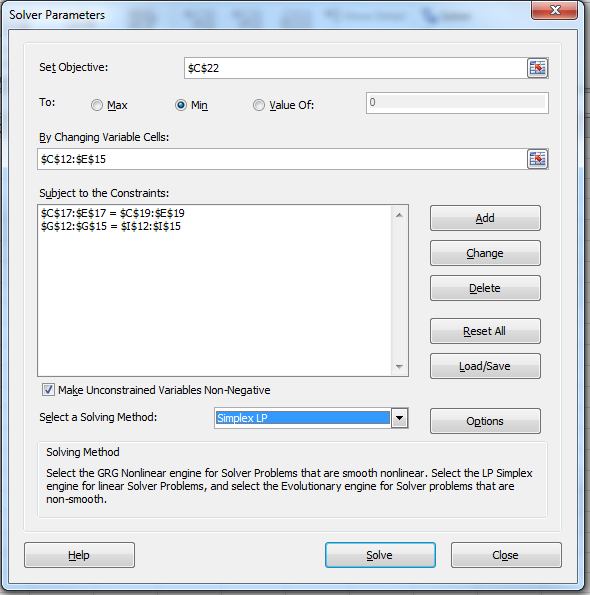 Step 4 After putting the values of objective function, constraints and variables in the above window, click on "Solve" tab.
Step 4 After putting the values of objective function, constraints and variables in the above window, click on "Solve" tab.
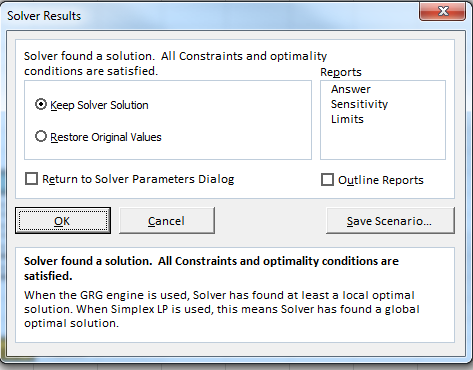 The resultant optimal solution for the given problem is as shown below:
The resultant optimal solution for the given problem is as shown below:
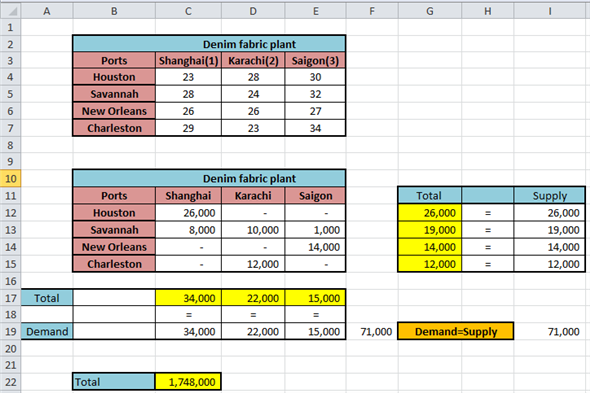 Therefore, the optimal shipment will be as shown below:
Therefore, the optimal shipment will be as shown below:
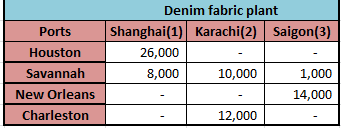 • Houston will supply 26,000 units to Shanghai.
• Houston will supply 26,000 units to Shanghai.
• Savannah will supply 8,000 units to Shanghai, 10,000 units to Karachi and 1,000 units to Saigon.
• New Orleans will supply 14,000 units to Saigon.
• Charleston will supply 12,000 units to Karachi.
At this schedule the total shipping cost will be minimum that is $ 1,748,000
Therefore,
Objective function:
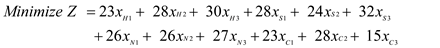 Subject to constraints:
Subject to constraints: Supply constraints H, S, N and C will be as shown below :
 Demand constraints at 1, 2, and 3 will be as shown below:
Demand constraints at 1, 2, and 3 will be as shown below: 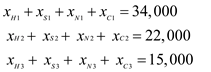 Non -negative Constraints
Non -negative Constraints  Formulate the problem as shown below:
Formulate the problem as shown below: Step 1 Enter the values of different variables, constraints and objective in Excel and use the formulas as shown below:
 Step 2 Use the formulas for each row and column as shown below:
Step 2 Use the formulas for each row and column as shown below: Step 3 Enter the value of the variables, constraints and objective function in Excel Solver, as shown below:
Step 3 Enter the value of the variables, constraints and objective function in Excel Solver, as shown below:  Step 4 After putting the values of objective function, constraints and variables in the above window, click on "Solve" tab.
Step 4 After putting the values of objective function, constraints and variables in the above window, click on "Solve" tab. The resultant optimal solution for the given problem is as shown below:
The resultant optimal solution for the given problem is as shown below:  Therefore, the optimal shipment will be as shown below:
Therefore, the optimal shipment will be as shown below:  • Houston will supply 26,000 units to Shanghai.
• Houston will supply 26,000 units to Shanghai.• Savannah will supply 8,000 units to Shanghai, 10,000 units to Karachi and 1,000 units to Saigon.
• New Orleans will supply 14,000 units to Saigon.
• Charleston will supply 12,000 units to Karachi.
At this schedule the total shipping cost will be minimum that is $ 1,748,000
4
The Midlands Field Produce Company contracts with potato farmers in Colorado, Minnesota, North Dakota, and Wisconsin for monthly potato shipments. Midlands picks up the potatoes at the farms and ships mostly by truck (and sometimes by rail) to its sorting and distribution centers in Ohio, Missouri, and Iowa. At these centers the potatoes are cleaned, rejects are discarded, and the potatoes are sorted according to size and quality. They are then shipped to combination plants and distribution centers in Virginia, Pennsylvania, Georgia, and Texas, where the company produces a variety of potato products and distributes bags of potatoes to stores. Exceptions are the Ohio distribution center, which will accept potatoes only from farms in Minnesota, North Dakota, and Wisconsin, and the Texas plant, which won't accept shipments from Ohio because of disagreements over delivery schedules and quality issues. Following are summaries of the shipping costs from the farms to the distribution centers and the processing and shipping costs from the distribution centers to the plants, as well as the available monthly supply at each farm, the processing capacity at the distribution centers, and the final demand at the plants (in bushels):
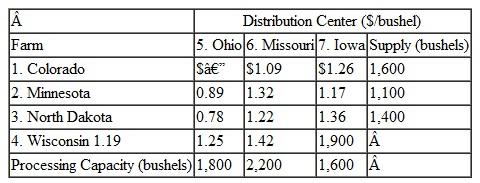
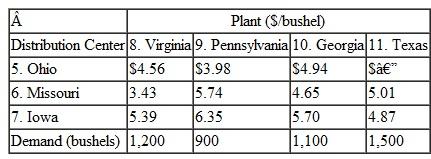 Formulate and solve a linear programming model to determine the optimal monthly shipments from the farms to the distribution centers and from the distribution centers to the plants to minimize total shipping and processing costs.
Formulate and solve a linear programming model to determine the optimal monthly shipments from the farms to the distribution centers and from the distribution centers to the plants to minimize total shipping and processing costs.

 Formulate and solve a linear programming model to determine the optimal monthly shipments from the farms to the distribution centers and from the distribution centers to the plants to minimize total shipping and processing costs.
Formulate and solve a linear programming model to determine the optimal monthly shipments from the farms to the distribution centers and from the distribution centers to the plants to minimize total shipping and processing costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
5
State University has planned six special catered events for the Saturday of its homecoming football game. The events include an alumni brunch, a parents' brunch, a booster club luncheon, a postgame party for season ticket holders, a lettermen's dinner, and a fund-raising dinner for major contributors. The university wants to use local catering firms as well as the university catering service to cater these events, and it has asked the caterers to bid on each event. The bids (in thousands of dollars) based on menu guidelines for the events prepared by the university are shown in the following table:
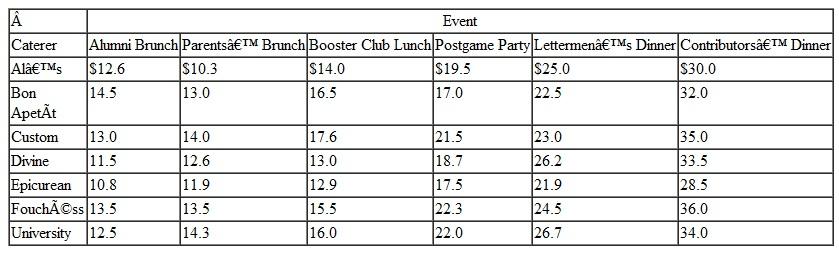 The Bon Apetít, Custom, and University caterers can handle two events, whereas each of the other four caterers can handle only one. The university is confident that all the caterers will do a highquality job, so it wants to select the caterers for the events that will result in the lowest total cost.
The Bon Apetít, Custom, and University caterers can handle two events, whereas each of the other four caterers can handle only one. The university is confident that all the caterers will do a highquality job, so it wants to select the caterers for the events that will result in the lowest total cost.
Determine the optimal selection of caterers to minimize total cost.
 The Bon Apetít, Custom, and University caterers can handle two events, whereas each of the other four caterers can handle only one. The university is confident that all the caterers will do a highquality job, so it wants to select the caterers for the events that will result in the lowest total cost.
The Bon Apetít, Custom, and University caterers can handle two events, whereas each of the other four caterers can handle only one. The university is confident that all the caterers will do a highquality job, so it wants to select the caterers for the events that will result in the lowest total cost.Determine the optimal selection of caterers to minimize total cost.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
6
Jim Huang and Roderick Wheeler were sales representatives in a computer store at a shopping mall in Arlington, Virginia, when they got the idea of going into business in the burgeoning and highly competitive microcomputer market. Jim went to Taiwan over the summer to visit relatives and made a contact with a new firm producing display monitors for microcomputers, which was looking for an East Coast distributor in America. Jim made a tentative deal with the firm to supply a maximum of 500 monitors per month and called Rod to see if he could find a building they could operate out of and some potential customers.
Rod went to work. The first thing he did was send bids to several universities in Maryland, Virginia, and Pennsylvania for contracts as an authorized vendor for monitors at the schools. Next, he started looking for a facility to operate from. Jim and his operation would provide minor physical modifications to the monitors, including some labeling, testing, packaging, and then storage in preparation for shipping. He knew he needed a building with good security, air-conditioning, and a loading dock. However, his search proved to be more difficult than he anticipated. Building space of the type and size he needed was very limited in the area and very expensive. Rod began to worry that he would not be able to find a suitable facility at all. He decided to look for space in the Virginia and Maryland suburbs and countryside; and although he found some good locations, the shipping costs out to those locations were extremely high.
Disheartened by his lack of success, Rod sought help from his sister-in-law Miriam, a local real estate agent. Rod poured out the details of his plight to Miriam over dinner at Rod's mother's house, and she was sympathetic. She told Rod that she owned a building in Arlington that might be just what he was looking for, and she would show it to him the next day. As promised, she showed him the ground floor of the building, and it was perfect. It had plenty of space, good security, and a nice office; furthermore, it was in an upscale shopping area with lots of good restaurants. Rod was elated; it was just the type of environment he had envisioned for them to set up their business in. However, his joy soured when he asked Miriam what the rent was. She said she had not worked out the details, but the rent would be around $100,000 per year. Rod was shocked, so Miriam said she would offer him an alternative: a storage fee of $10 per monitor for every monitor purchased and in stock the first month of operation, with an increase of $2 per month per unit for the remainder of the year. Miriam explained that based on what he told her about the business, they would not have any sales until the universities opened around the end of August or the first of September, and that their sales would fall off to nothing in May or June. She said her offer meant that she would share in their success or failure. If they ended up with some university contracts, she would reap a reward along with them; if they did not sell many monitors, she would lose on the deal. But in the summer months after school ended, if they had no monitors in stock, they would pay her nothing.
Rod mulled this over, and it sounded fair. He loved the building. Also, he liked the idea that they would not be indebted for a flat lease payment and that the rent was essentially on a per-unit basis. If they failed, at least they would not be stuck with a huge lease. So he agreed to Miriam's offer.
When Jim returned from Taiwan, he was skeptical about Rod's lease arrangement with Miriam. He was chagrined that Rod hadn't performed a more thorough analysis of the costs, but Rod explained that it was pretty hard to do an analysis when he did not know their costs, potential sales, or selling price. Jim said he had a point, and his concern was somewhat offset by the fact that Rod had gotten contracts with five universities as an authorized vendor for monitors at a selling price of $180 per unit. So the two sat down to begin planning their operation.
First, Jim said he had thought of a name for their enterprise, Hawk Systems, Inc., which he said stood for Huang and Wheeler Computers. When Rod asked how Jim got a k out of computers , Jim cited poetic license.
Jim said that he had figured that the total cost of the units for them-including the purchase of the units, shipping, and their own material, labor, and administrative costs-would be $100 per unit during the first 4 months but would then drop to $90 per month for the following 4 months and, finally, to $85 per month for the remainder of the year. Jim said that the Taiwan firm was anticipating being able to lower the purchase price because its production costs would go down as it gained experience.
Jim thought their own costs would go down, too. He also explained that they would not be able to return any items, so it was important that they develop a good order plan that would minimize costs. This was now much more important than Jim had originally thought because of their peculiar lease arrangement based on their inventory level. Rod said that he had done some research on past computer sales at the universities they had contracted with and had come up with the following sales forecast for the next 9 months of the academic year (from September through May):
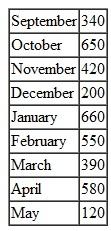 Rod explained to Jim that computer equipment purchases at universities go up in the fall, then drop until January, and then peak again in April, just before university budgets are exhausted at the end of the academic year.
Rod explained to Jim that computer equipment purchases at universities go up in the fall, then drop until January, and then peak again in April, just before university budgets are exhausted at the end of the academic year.
Jim then asked Rod what kind of monthly ordering schedule from Taiwan they should develop to meet demand while minimizing their costs. Rod said that it was a difficult question, but he remembered that when he was in college in a management science course, he had seen a production schedule developed using a transportation model. Jim suggested he get out his old textbook and get busy, or they would be turning over all their profits to Miriam.
However, before Rod was able to develop a schedule, Jim got a call from the Taiwan firm, saying that it had gotten some more business later in the year and it could no longer supply up to 500 units per month. Instead, it could supply 700 monitors for the first 4 months and 300 for the next 5. Jim and Rod worried about what this would do to their inventory costs.
A. Formulate and solve a transportation model to determine an optimal monthly ordering and distribution schedule for Hawk Systems that will minimize costs.
B. If Hawk Systems has to borrow approximately $200,000 to start up the business, will it end up making anything the first year
C. What will the change in the supply pattern from the Taiwan firm cost Hawk Systems
D. How did Miriam fare with her alternative lease arrangement Would she have been better off with a flat $100,000 lease payment
Rod went to work. The first thing he did was send bids to several universities in Maryland, Virginia, and Pennsylvania for contracts as an authorized vendor for monitors at the schools. Next, he started looking for a facility to operate from. Jim and his operation would provide minor physical modifications to the monitors, including some labeling, testing, packaging, and then storage in preparation for shipping. He knew he needed a building with good security, air-conditioning, and a loading dock. However, his search proved to be more difficult than he anticipated. Building space of the type and size he needed was very limited in the area and very expensive. Rod began to worry that he would not be able to find a suitable facility at all. He decided to look for space in the Virginia and Maryland suburbs and countryside; and although he found some good locations, the shipping costs out to those locations were extremely high.
Disheartened by his lack of success, Rod sought help from his sister-in-law Miriam, a local real estate agent. Rod poured out the details of his plight to Miriam over dinner at Rod's mother's house, and she was sympathetic. She told Rod that she owned a building in Arlington that might be just what he was looking for, and she would show it to him the next day. As promised, she showed him the ground floor of the building, and it was perfect. It had plenty of space, good security, and a nice office; furthermore, it was in an upscale shopping area with lots of good restaurants. Rod was elated; it was just the type of environment he had envisioned for them to set up their business in. However, his joy soured when he asked Miriam what the rent was. She said she had not worked out the details, but the rent would be around $100,000 per year. Rod was shocked, so Miriam said she would offer him an alternative: a storage fee of $10 per monitor for every monitor purchased and in stock the first month of operation, with an increase of $2 per month per unit for the remainder of the year. Miriam explained that based on what he told her about the business, they would not have any sales until the universities opened around the end of August or the first of September, and that their sales would fall off to nothing in May or June. She said her offer meant that she would share in their success or failure. If they ended up with some university contracts, she would reap a reward along with them; if they did not sell many monitors, she would lose on the deal. But in the summer months after school ended, if they had no monitors in stock, they would pay her nothing.
Rod mulled this over, and it sounded fair. He loved the building. Also, he liked the idea that they would not be indebted for a flat lease payment and that the rent was essentially on a per-unit basis. If they failed, at least they would not be stuck with a huge lease. So he agreed to Miriam's offer.
When Jim returned from Taiwan, he was skeptical about Rod's lease arrangement with Miriam. He was chagrined that Rod hadn't performed a more thorough analysis of the costs, but Rod explained that it was pretty hard to do an analysis when he did not know their costs, potential sales, or selling price. Jim said he had a point, and his concern was somewhat offset by the fact that Rod had gotten contracts with five universities as an authorized vendor for monitors at a selling price of $180 per unit. So the two sat down to begin planning their operation.
First, Jim said he had thought of a name for their enterprise, Hawk Systems, Inc., which he said stood for Huang and Wheeler Computers. When Rod asked how Jim got a k out of computers , Jim cited poetic license.
Jim said that he had figured that the total cost of the units for them-including the purchase of the units, shipping, and their own material, labor, and administrative costs-would be $100 per unit during the first 4 months but would then drop to $90 per month for the following 4 months and, finally, to $85 per month for the remainder of the year. Jim said that the Taiwan firm was anticipating being able to lower the purchase price because its production costs would go down as it gained experience.
Jim thought their own costs would go down, too. He also explained that they would not be able to return any items, so it was important that they develop a good order plan that would minimize costs. This was now much more important than Jim had originally thought because of their peculiar lease arrangement based on their inventory level. Rod said that he had done some research on past computer sales at the universities they had contracted with and had come up with the following sales forecast for the next 9 months of the academic year (from September through May):
 Rod explained to Jim that computer equipment purchases at universities go up in the fall, then drop until January, and then peak again in April, just before university budgets are exhausted at the end of the academic year.
Rod explained to Jim that computer equipment purchases at universities go up in the fall, then drop until January, and then peak again in April, just before university budgets are exhausted at the end of the academic year.Jim then asked Rod what kind of monthly ordering schedule from Taiwan they should develop to meet demand while minimizing their costs. Rod said that it was a difficult question, but he remembered that when he was in college in a management science course, he had seen a production schedule developed using a transportation model. Jim suggested he get out his old textbook and get busy, or they would be turning over all their profits to Miriam.
However, before Rod was able to develop a schedule, Jim got a call from the Taiwan firm, saying that it had gotten some more business later in the year and it could no longer supply up to 500 units per month. Instead, it could supply 700 monitors for the first 4 months and 300 for the next 5. Jim and Rod worried about what this would do to their inventory costs.
A. Formulate and solve a transportation model to determine an optimal monthly ordering and distribution schedule for Hawk Systems that will minimize costs.
B. If Hawk Systems has to borrow approximately $200,000 to start up the business, will it end up making anything the first year
C. What will the change in the supply pattern from the Taiwan firm cost Hawk Systems
D. How did Miriam fare with her alternative lease arrangement Would she have been better off with a flat $100,000 lease payment

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
7
In Problem, the Shotz Beer Company management negotiated a new shipping contract with a trucking firm between its Tampa brewery and its distributor in Kentucky. This contract reduces the shipping cost per barrel from $0.80 per barrel to $0.65 per barrel. How will this cost change affect the optimal solution
Problem
The Shotz Beer Company has breweries in two cities; the breweries can supply the following numbers of barrels of draft beer to the company's distributors each month:
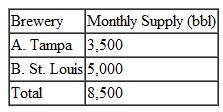 The distributors, which are spread throughout six states, have the following total monthly demand:
The distributors, which are spread throughout six states, have the following total monthly demand:
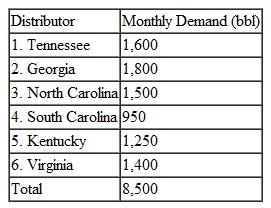 The company must pay the following shipping costs per barrel:
The company must pay the following shipping costs per barrel:
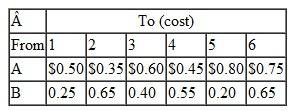 Solve this problem by using the computer.
Solve this problem by using the computer.
Problem
The Shotz Beer Company has breweries in two cities; the breweries can supply the following numbers of barrels of draft beer to the company's distributors each month:
 The distributors, which are spread throughout six states, have the following total monthly demand:
The distributors, which are spread throughout six states, have the following total monthly demand: The company must pay the following shipping costs per barrel:
The company must pay the following shipping costs per barrel: Solve this problem by using the computer.
Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
8
Suntrek in Problem manufactures denim fabric at its factories in Shanghai, Karachi, and Saigon and ships it to its denim jeans manufacturing facilities in China, India, Japan, Turkey, and Italy. A bale of cotton will produce approximately 325 yards of denim fabric. Following are the fabric demand at each denim jeans plant and the shipping and handling costs per yard from the fabric manufacturing facilities to the jeans plants:
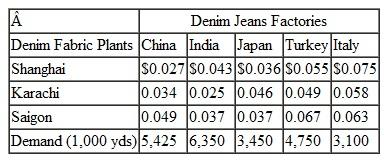 Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Problem
Suntrek in Problem 26 ships the cotton it has purchased from the U.S. ports to overseas ports in Shanghai, Karachi, and Saigon, where its denim fabric factories are also located. The shipping and handling costs per bale of cotton from each U.S. port to each of Suntrek's overseas factories and the demand at these factories are as follows:
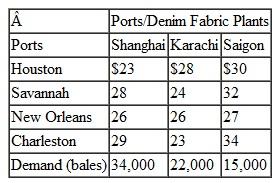 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.
 Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.Problem
Suntrek in Problem 26 ships the cotton it has purchased from the U.S. ports to overseas ports in Shanghai, Karachi, and Saigon, where its denim fabric factories are also located. The shipping and handling costs per bale of cotton from each U.S. port to each of Suntrek's overseas factories and the demand at these factories are as follows:
 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
9
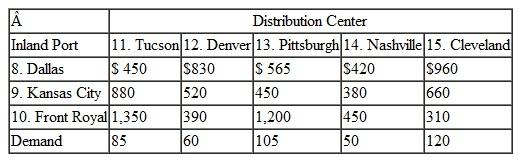
KanTech Corporation is a global distributor of electrical parts and components. Its customers are electronics companies in the United States, including computer manufacturers and audio/ visual product manufacturers. The company contracts to purchase components and parts from manufacturers in Russia, Eastern and Western Europe, and the Mediterranean, and it has them delivered to warehouses in three European ports, Gdansk, Hamburg, and Lisbon. The various components and parts are loaded into containers based on demand from U.S. customers. Each port has a limited fixed number of containers available each month. The containers are then shipped overseas by container ships to the ports of Norfolk, Jacksonville, New Orleans, and Galveston. From these seaports, the containers are typically coupled with trucks and hauled to inland ports in Front Royal (Virginia), Kansas City, and Dallas. There are a fixed number of freight haulers available at each port each month. These inland ports are sometimes called "freight villages," or intermodal junctions, where the containers are collected and transferred from one transport mode to another (i.e., from truck to rail or vice versa). From the inland ports, the containers are transported to KanTech's distribution centers in Tucson, Pittsburgh, Denver, Nashville, and Cleveland. Following are the handling and shipping costs ($/container) between each of the embarkation and destination points along this overseas supply chain and the available containers at each port:
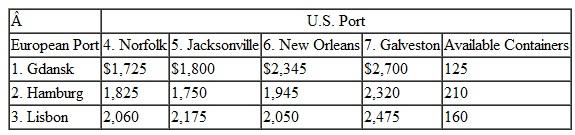
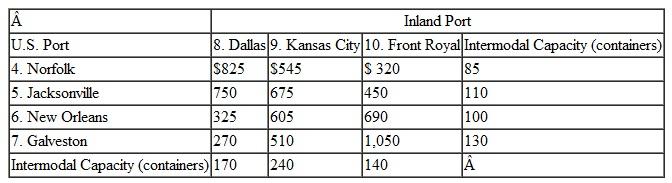
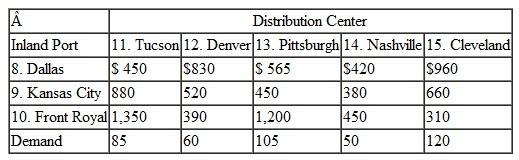 Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.


 Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
10
A university department head has five instructors to be assigned to four different courses. All the instructors have taught the courses in the past and have been evaluated by the students. The rating for each instructor for each course is given in the following table (a perfect score is 100):
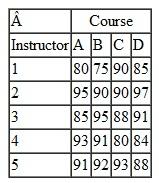 The department head wants to know the optimal assignment of instructors to courses to maximize the overall average evaluation. The instructor who is not assigned to teach a course will be assigned to grade exams.
The department head wants to know the optimal assignment of instructors to courses to maximize the overall average evaluation. The instructor who is not assigned to teach a course will be assigned to grade exams.
 The department head wants to know the optimal assignment of instructors to courses to maximize the overall average evaluation. The instructor who is not assigned to teach a course will be assigned to grade exams.
The department head wants to know the optimal assignment of instructors to courses to maximize the overall average evaluation. The instructor who is not assigned to teach a course will be assigned to grade exams.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
11
Rachel Sundusky is the manager of the South-Atlantic office of the Stateline Shipping and Transport Company. She is in the process of negotiating a new shipping contract with Polychem, a company that manufactures chemicals for industrial use. Polychem wants Stateline to pick up and transport waste products from its six plants to three waste disposal sites. Rachel is very concerned about this proposed arrangement. The chemical wastes that will be hauled can be hazardous to humans and the environment if they leak. In addition, a number of towns and communities in the region where the plants are located prohibit hazardous materials from being shipped through their municipal limits. Thus, not only will the shipments have to be handled carefully and transported at reduced speeds, they will also have to traverse circuitous routes in many cases.
Rachel has estimated the cost of shipping a barrel of waste from each of the six plants to each of the three waste disposal sites as shown in the following table:
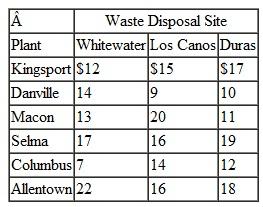 The plants generate the following amounts of waste products each week:
The plants generate the following amounts of waste products each week:
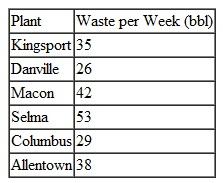 The three waste disposal sites at Whitewater, Los Canos, and Duras can accommodate a maximum of 65, 80, and 105 barrels per week, respectively.
The three waste disposal sites at Whitewater, Los Canos, and Duras can accommodate a maximum of 65, 80, and 105 barrels per week, respectively.
In addition to shipping directly from each of the six plants to one of the three waste disposal sites, Rachel is also considering using each of the plants and waste disposal sites as intermediate shipping points. Trucks would be able to drop a load at a plant or disposal site to be picked up and carried on to the final destination by another truck, and vice versa. Stateline would not incur any handling costs because Polychem has agreed to take care of all local handling of the waste materials at the plants and the waste disposal sites. In other words, the only cost Stateline incurs is the actual transportation cost. So Rachel wants to be able to consider the possibility that it may be cheaper to drop and pick up loads at intermediate points rather than ship them directly.
Rachel estimates the shipping costs per barrel between each of the six plants to be as follows:
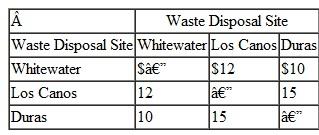
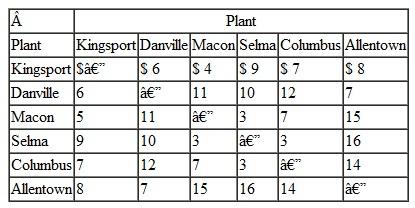 The estimated shipping cost per barrel between each of the three waste disposal sites is as follows:
The estimated shipping cost per barrel between each of the three waste disposal sites is as follows:
 Rachel wants to determine the shipping routes that will minimize Stateline's total cost in order to develop a contract proposal to submit to Polychem for waste disposal. She particularly wants to know if it would be cheaper to ship directly from the plants to the waste sites or if she should drop and pick up some loads at the various plants and waste sites. Develop a model to assist Rachel and solve the model to determine the optimal routes.
Rachel wants to determine the shipping routes that will minimize Stateline's total cost in order to develop a contract proposal to submit to Polychem for waste disposal. She particularly wants to know if it would be cheaper to ship directly from the plants to the waste sites or if she should drop and pick up some loads at the various plants and waste sites. Develop a model to assist Rachel and solve the model to determine the optimal routes.
Rachel has estimated the cost of shipping a barrel of waste from each of the six plants to each of the three waste disposal sites as shown in the following table:
 The plants generate the following amounts of waste products each week:
The plants generate the following amounts of waste products each week: The three waste disposal sites at Whitewater, Los Canos, and Duras can accommodate a maximum of 65, 80, and 105 barrels per week, respectively.
The three waste disposal sites at Whitewater, Los Canos, and Duras can accommodate a maximum of 65, 80, and 105 barrels per week, respectively.In addition to shipping directly from each of the six plants to one of the three waste disposal sites, Rachel is also considering using each of the plants and waste disposal sites as intermediate shipping points. Trucks would be able to drop a load at a plant or disposal site to be picked up and carried on to the final destination by another truck, and vice versa. Stateline would not incur any handling costs because Polychem has agreed to take care of all local handling of the waste materials at the plants and the waste disposal sites. In other words, the only cost Stateline incurs is the actual transportation cost. So Rachel wants to be able to consider the possibility that it may be cheaper to drop and pick up loads at intermediate points rather than ship them directly.
Rachel estimates the shipping costs per barrel between each of the six plants to be as follows:
 The estimated shipping cost per barrel between each of the three waste disposal sites is as follows:
The estimated shipping cost per barrel between each of the three waste disposal sites is as follows: Rachel wants to determine the shipping routes that will minimize Stateline's total cost in order to develop a contract proposal to submit to Polychem for waste disposal. She particularly wants to know if it would be cheaper to ship directly from the plants to the waste sites or if she should drop and pick up some loads at the various plants and waste sites. Develop a model to assist Rachel and solve the model to determine the optimal routes.
Rachel wants to determine the shipping routes that will minimize Stateline's total cost in order to develop a contract proposal to submit to Polychem for waste disposal. She particularly wants to know if it would be cheaper to ship directly from the plants to the waste sites or if she should drop and pick up some loads at the various plants and waste sites. Develop a model to assist Rachel and solve the model to determine the optimal routes.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
12
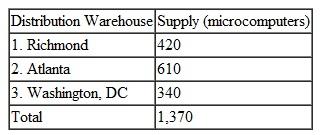
Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year:
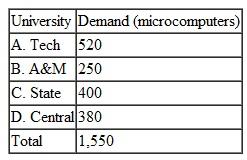
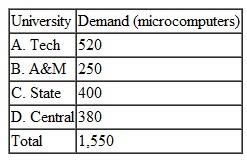
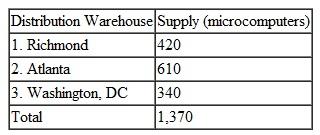 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
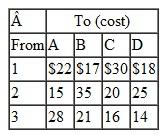
 The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows:
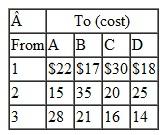 Solve this problem by using the computer.
Solve this problem by using the computer.
 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year: The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows: Solve this problem by using the computer.
Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
13
Suntrek in Problem supplies its finished denim jeans to its customers' distribution centers in the United States in New York and New Orleans, and in Europe in Bristol and Marseilles. Denim jeans require 1.5 yards of denim fabric. Following are the contracted deliveries of jeans for each of Suntrek's customer's distribution centers, and the shipping and handling costs per jeans from the jeans factories to the distribution centers:
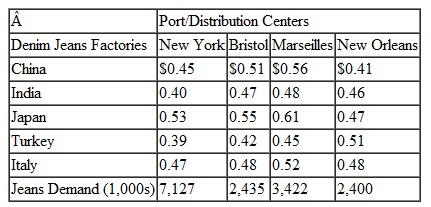 Determine the optimal shipments from each jeans factory to each distribution center and the optimal total shipping cost.
Determine the optimal shipments from each jeans factory to each distribution center and the optimal total shipping cost.
Suntrek in Problem 27 manufactures denim fabric at its factories in Shanghai, Karachi, and Saigon and ships it to its denim jeans manufacturing facilities in China, India, Japan, Turkey, and Italy. A bale of cotton will produce approximately 325 yards of denim fabric. Following are the fabric demand at each denim jeans plant and the shipping and handling costs per yard from the fabric manufacturing facilities to the jeans plants:
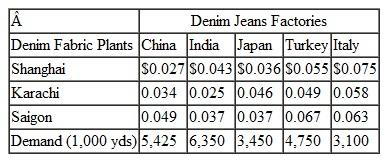 Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
 Determine the optimal shipments from each jeans factory to each distribution center and the optimal total shipping cost.
Determine the optimal shipments from each jeans factory to each distribution center and the optimal total shipping cost.Suntrek in Problem 27 manufactures denim fabric at its factories in Shanghai, Karachi, and Saigon and ships it to its denim jeans manufacturing facilities in China, India, Japan, Turkey, and Italy. A bale of cotton will produce approximately 325 yards of denim fabric. Following are the fabric demand at each denim jeans plant and the shipping and handling costs per yard from the fabric manufacturing facilities to the jeans plants:
 Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Determine the optimal shipments from each of the fabric plants to the denim jeans manufacturing facilities and the minimum total shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
14
In Problem, KanTech Corporation is just as concerned that its U.S. distributors receive shipments in the minimum amount of time as they are about minimizing their shipping costs. Suppose that each U.S. distributor receives one major container shipment each month. Following are summaries of the shipping times (in days) between each of the embarkation and destination points along KanTech's overseas supply chain. These times encompass not only travel time but also processing, loading, and unloading times at each port:
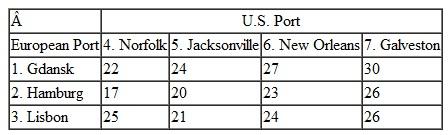
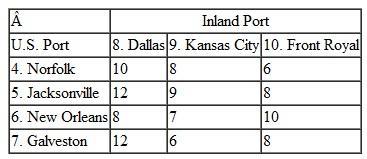
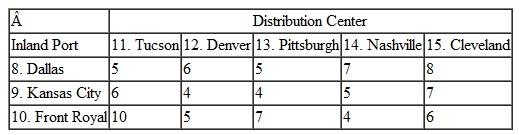 a. Formulate and solve a linear programming model to determine the optimal shipping route for each distribution center along this supply chain that will result in the minimum total shipping time. Determine the shipping route and time for each U.S. distributor.
a. Formulate and solve a linear programming model to determine the optimal shipping route for each distribution center along this supply chain that will result in the minimum total shipping time. Determine the shipping route and time for each U.S. distributor.
b. Suppose the European ports can accommodate only three shipments each. How will this affect the solution in part (a)
Problem
KanTech Corporation is a global distributor of electrical parts and components. Its customers are electronics companies in the United States, including computer manufacturers and audio/ visual product manufacturers. The company contracts to purchase components and parts from manufacturers in Russia, Eastern and Western Europe, and the Mediterranean, and it has them delivered to warehouses in three European ports, Gdansk, Hamburg, and Lisbon. The various components and parts are loaded into containers based on demand from U.S. customers. Each port has a limited fixed number of containers available each month. The containers are then shipped overseas by container ships to the ports of Norfolk, Jacksonville, New Orleans, and Galveston. From these seaports, the containers are typically coupled with trucks and hauled to inland ports in Front Royal (Virginia), Kansas City, and Dallas. There are a fixed number of freight haulers available at each port each month. These inland ports are sometimes called "freight villages," or intermodal junctions, where the containers are collected and transferred from one transport mode to another (i.e., from truck to rail or vice versa). From the inland ports, the containers are transported to KanTech's distribution centers in Tucson, Pittsburgh, Denver, Nashville, and Cleveland. Following are the handling and shipping costs ($/container) between each of the embarkation and destination points along this overseas supply chain and the available containers at each port:
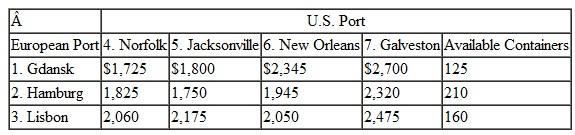
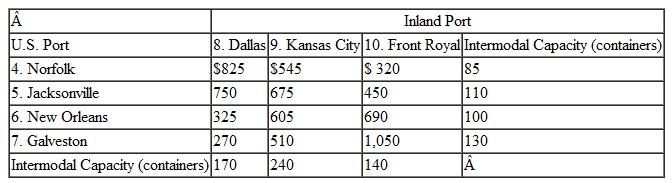
 Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.


 a. Formulate and solve a linear programming model to determine the optimal shipping route for each distribution center along this supply chain that will result in the minimum total shipping time. Determine the shipping route and time for each U.S. distributor.
a. Formulate and solve a linear programming model to determine the optimal shipping route for each distribution center along this supply chain that will result in the minimum total shipping time. Determine the shipping route and time for each U.S. distributor.b. Suppose the European ports can accommodate only three shipments each. How will this affect the solution in part (a)
Problem
KanTech Corporation is a global distributor of electrical parts and components. Its customers are electronics companies in the United States, including computer manufacturers and audio/ visual product manufacturers. The company contracts to purchase components and parts from manufacturers in Russia, Eastern and Western Europe, and the Mediterranean, and it has them delivered to warehouses in three European ports, Gdansk, Hamburg, and Lisbon. The various components and parts are loaded into containers based on demand from U.S. customers. Each port has a limited fixed number of containers available each month. The containers are then shipped overseas by container ships to the ports of Norfolk, Jacksonville, New Orleans, and Galveston. From these seaports, the containers are typically coupled with trucks and hauled to inland ports in Front Royal (Virginia), Kansas City, and Dallas. There are a fixed number of freight haulers available at each port each month. These inland ports are sometimes called "freight villages," or intermodal junctions, where the containers are collected and transferred from one transport mode to another (i.e., from truck to rail or vice versa). From the inland ports, the containers are transported to KanTech's distribution centers in Tucson, Pittsburgh, Denver, Nashville, and Cleveland. Following are the handling and shipping costs ($/container) between each of the embarkation and destination points along this overseas supply chain and the available containers at each port:


 Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Formulate and solve a linear programming model to determine the optimal shipments from each point of embarkation to each destination along this supply chain that will result in the minimum total shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
15
The coach of the women's swim team at State University is preparing for the conference swim meet and must choose the four swimmers she will assign to the 800-meter medley relay team. The medley relay consists of four strokes-backstroke, breaststroke, butterfly, and freestyle. The coach has computed the average times (in minutes) each of her top six swimmers has achieved in each of the four strokes for 200 meters in previous swim meets during the season, as follows:
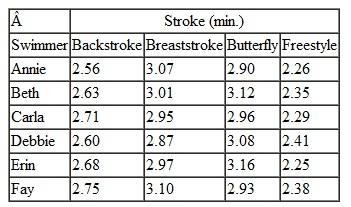 Determine for the coach the medley relay team and its total expected relay time.
Determine for the coach the medley relay team and its total expected relay time.
 Determine for the coach the medley relay team and its total expected relay time.
Determine for the coach the medley relay team and its total expected relay time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
16
The management science and information technology department at Tech offers between 36 and 40 three-hour course sections each semester. Some of the courses are taught by graduate student instructors, whereas 20 of the course sections are taught by the 10 regular, tenured faculty in the department. Before the beginning of each year, the department head sends the faculty a questionnaire, asking them to rate their preference for each course using a scale from 1 to 5, where 1 is "strongly preferred," 2 is "preferred but not as strongly as 1," 3 is "neutral," 4 is "prefer not to teach but not strongly," and 5 is "strongly prefer not to teach this course." The faculty have returned their preferences, as follows:
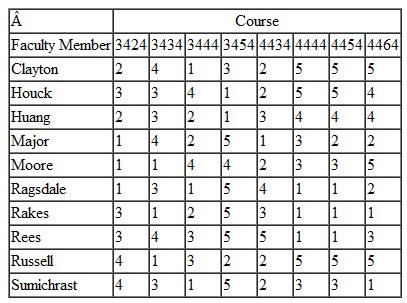 For the fall semester the department will offer two sections each of 3424 and 4464; three sections of 3434, 3444, 4434, 4444, and 4454; and one section of 3454.
For the fall semester the department will offer two sections each of 3424 and 4464; three sections of 3434, 3444, 4434, 4444, and 4454; and one section of 3454.
The normal semester teaching load for a regular faculty member is two sections. (Once the department head determines the courses, he will assign the faculty he schedules the course times so they will not conflict.) Help the department head determine a teaching schedule that will satisfy faculty teaching preferences to the greatest degree possible.
 For the fall semester the department will offer two sections each of 3424 and 4464; three sections of 3434, 3444, 4434, 4444, and 4454; and one section of 3454.
For the fall semester the department will offer two sections each of 3424 and 4464; three sections of 3434, 3444, 4434, 4444, and 4454; and one section of 3454.The normal semester teaching load for a regular faculty member is two sections. (Once the department head determines the courses, he will assign the faculty he schedules the course times so they will not conflict.) Help the department head determine a teaching schedule that will satisfy faculty teaching preferences to the greatest degree possible.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
17
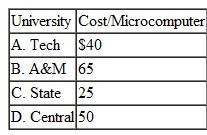
In Problem, Computers Unlimited wants to better meet demand at the four universities it supplies. It is considering two alternatives: (1) expand its warehouse at Richmond to a capacity of 600, at a cost equivalent to an additional $6 in handling and shipping per unit; or (2) purchase a new warehouse in Charlotte that can supply 300 units with shipping costs of $19 to Tech, $26 to A M, $22 to State, and $16 to Central. Which alternative should management select, based solely on transportation costs (i.e., no capital costs)
Problem
Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year:
 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
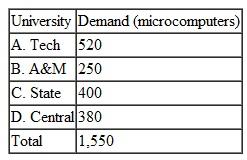 The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows:
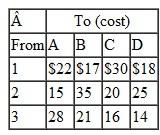 Solve this problem by using the computer.
Solve this problem by using the computer.
Problem
Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year:
 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year: The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows: Solve this problem by using the computer.
Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
18
PM Computer Services produces personal computers from component parts it buys on the open market. The company can produce a maximum of 300 personal computers per month. PM wants to determine its production schedule for the first 6 months of the new year. The cost to produce a personal computer in January will be $1,200. However, PM knows the cost of component parts will decline each month so that the overall cost to produce a PC will be 5% less each month. The cost of holding a computer in inventory is $15 per unit per month. Following is the demand for the company's computers each month:
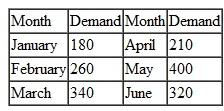 Determine a production schedule for PM that will minimize total cost.
Determine a production schedule for PM that will minimize total cost.
 Determine a production schedule for PM that will minimize total cost.
Determine a production schedule for PM that will minimize total cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
19
Blue Mountain Coffee Company produces various blends of Free Trade, organic specialty coffees that it sells to wholesale customers. The company imports 25 million pounds of coffee beans annually from coffee plantations in Brazil, Indonesia, Kenya, Colombia, Côte d'Ivoire, and Guatemala. The beans are shipped from these countries to U.S. ports in Galveston, New Orleans, Savannah, and Jacksonville, where they are loaded onto container trucks and shipped to the company's plant in Vermont. The shipping costs (in dollars per million pounds) from the countries to the U.S. ports, the amount of beans (in millions of pounds) contracted from the growers in each country, and the port capacities are shown in the following table:
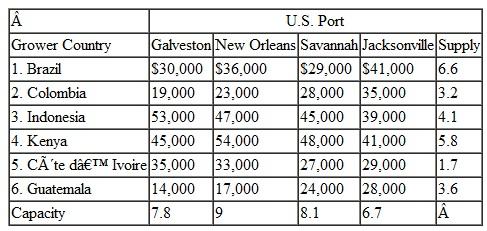 The shipping costs from each port to the plant in Vermont are shown in the following table:
The shipping costs from each port to the plant in Vermont are shown in the following table:
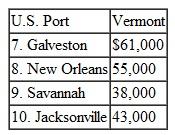 Determine the optimal shipments from the grower countries to the plant in Vermont that will minimize shipping costs.
Determine the optimal shipments from the grower countries to the plant in Vermont that will minimize shipping costs.
 The shipping costs from each port to the plant in Vermont are shown in the following table:
The shipping costs from each port to the plant in Vermont are shown in the following table: Determine the optimal shipments from the grower countries to the plant in Vermont that will minimize shipping costs.
Determine the optimal shipments from the grower countries to the plant in Vermont that will minimize shipping costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
20
Biggio's Department Store has six employees available to assign to four departments in the store-home furnishings, china, appliances, and jewelry. Most of the six employees have worked in each of the four departments on several occasions in the past and have demonstrated that they perform better in some departments than in others. The average daily sales for each of the six employees in each of the four departments are shown in the following table:
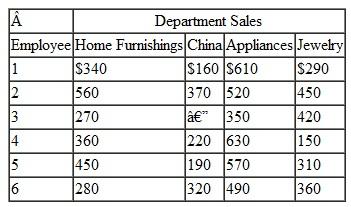 Employee 3 has not worked in the china department before, so the manager does not want to assign this employee to china.
Employee 3 has not worked in the china department before, so the manager does not want to assign this employee to china.
Determine which employee to assign to each department and indicate the total expected daily sales.
 Employee 3 has not worked in the china department before, so the manager does not want to assign this employee to china.
Employee 3 has not worked in the china department before, so the manager does not want to assign this employee to china.Determine which employee to assign to each department and indicate the total expected daily sales.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
21
Each spring the Tech Student Government Association (SGA) organizes an event called "Give Back Weekends." The SGA solicits student teams to work on projects for residents in the university community on four consecutive Saturdays in April. The coed student teams generally are made up of three to five students from various dormitory groups, fraternities, sororities, and student clubs and organizations. The SGA invites projects from the residents by sending out a form during the winter enclosed in the residents' town utilities bills and through newspaper ads and its Internet site. The residents complete the form that briefly describes the work at their home that they want done, which is primarily yard cleanup work, plus odd jobs like window washing, painting, and hauling away unwanted items to Goodwill or the dump. Once the forms are submitted the SGA event coordinators visit the homes with the team leaders to assess the work involved and the team leaders provide an estimate of the time that will be required for their team to complete the project. The time to complete a project will vary between the teams because of the different number of team members, the skills of the team, and the physical make-up of the team, since most projects involve manual labor. Following are the time estimates (in hours) submitted by the six teams available to work on the projects for the 12 projects for the first Saturday in the event:
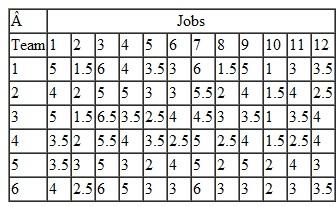 The SGA's primary objective is to complete all 12 projects, if possible. Each team can work on multiple projects but cannot work more than 8 hours on Saturday. The SGA wants each team to be involved by working on at least one project.
The SGA's primary objective is to complete all 12 projects, if possible. Each team can work on multiple projects but cannot work more than 8 hours on Saturday. The SGA wants each team to be involved by working on at least one project.
a. Determine the optimal assignment of teams to projects that will maximize the number of projects completed.
b. Determine the assignment of teams to projects if the SGA wants to complete all 12 projects while minimizing the total time required for all six teams. What, if any, is the difference between the two solutions. What is the average time per team
 The SGA's primary objective is to complete all 12 projects, if possible. Each team can work on multiple projects but cannot work more than 8 hours on Saturday. The SGA wants each team to be involved by working on at least one project.
The SGA's primary objective is to complete all 12 projects, if possible. Each team can work on multiple projects but cannot work more than 8 hours on Saturday. The SGA wants each team to be involved by working on at least one project.a. Determine the optimal assignment of teams to projects that will maximize the number of projects completed.
b. Determine the assignment of teams to projects if the SGA wants to complete all 12 projects while minimizing the total time required for all six teams. What, if any, is the difference between the two solutions. What is the average time per team

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
22
Computers Unlimited in Problem has determined that when it is unable to meet the demand for microcomputers at the universities it supplies, the universities tend to purchase microcomputers elsewhere in the future. Thus, the firm has estimated a shortage cost for each microcomputer demanded but not supplied that reflects the loss of future sales and goodwill. These costs for each university are as follows:
 Solve Problem with these shortage costs included. Compute the total transportation cost and the total shortage cost.
Solve Problem with these shortage costs included. Compute the total transportation cost and the total shortage cost.
Problem
Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year:
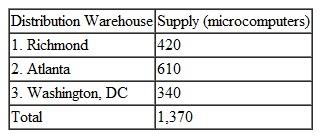 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
 The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows:
 Solve this problem by using the computer.
Solve this problem by using the computer.
 Solve Problem with these shortage costs included. Compute the total transportation cost and the total shortage cost.
Solve Problem with these shortage costs included. Compute the total transportation cost and the total shortage cost.Problem
Computers Unlimited sells microcomputers to universities and colleges on the East Coast and ships them from three distribution warehouses. The firm is able to supply the following numbers of microcomputers to the universities by the beginning of the academic year:
 Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year:
Four universities have ordered microcomputers that must be delivered and installed by the beginning of the academic year: The shipping and installation costs per microcomputer from each distributor to each university are as follows:
The shipping and installation costs per microcomputer from each distributor to each university are as follows: Solve this problem by using the computer.
Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
23
In Problem, suppose that the demand for personal computers increased each month, as follows:
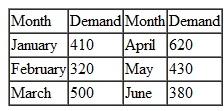 In addition to the regular production capacity of 300 units per month, PM Computer Services can also produce an additional 200 computers per month by using overtime. Overtime production adds 20% to the cost of a personal computer.
In addition to the regular production capacity of 300 units per month, PM Computer Services can also produce an additional 200 computers per month by using overtime. Overtime production adds 20% to the cost of a personal computer.
Determine a production schedule for PM that will minimize total cost.
Problem
PM Computer Services produces personal computers from component parts it buys on the open market. The company can produce a maximum of 300 personal computers per month. PM wants to determine its production schedule for the first 6 months of the new year. The cost to produce a personal computer in January will be $1,200. However, PM knows the cost of component parts will decline each month so that the overall cost to produce a PC will be 5% less each month. The cost of holding a computer in inventory is $15 per unit per month. Following is the demand for the company's computers each month:
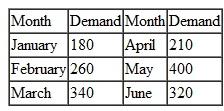 Determine a production schedule for PM that will minimize total cost.
Determine a production schedule for PM that will minimize total cost.
 In addition to the regular production capacity of 300 units per month, PM Computer Services can also produce an additional 200 computers per month by using overtime. Overtime production adds 20% to the cost of a personal computer.
In addition to the regular production capacity of 300 units per month, PM Computer Services can also produce an additional 200 computers per month by using overtime. Overtime production adds 20% to the cost of a personal computer.Determine a production schedule for PM that will minimize total cost.
Problem
PM Computer Services produces personal computers from component parts it buys on the open market. The company can produce a maximum of 300 personal computers per month. PM wants to determine its production schedule for the first 6 months of the new year. The cost to produce a personal computer in January will be $1,200. However, PM knows the cost of component parts will decline each month so that the overall cost to produce a PC will be 5% less each month. The cost of holding a computer in inventory is $15 per unit per month. Following is the demand for the company's computers each month:
 Determine a production schedule for PM that will minimize total cost.
Determine a production schedule for PM that will minimize total cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
24
The Pinnacle Company is a U.S.-based manufacturer of furniture and appliances that offshored all of its actual manufacturing operations to Asia about a decade ago. It then set up distribution centers at various locations on the East Coast, near ports where its items were imported on container ships. In many cases, Pinnacle's appliances and furniture arrive partially assembled, and the company completes the assembly at its distribution centers before sending the finished products to retailers. For example, appliance motors, electric controls, housings, and furniture pieces might arrive from different Asian manufacturers in separate containers. Recently Pinnacle began exporting its products to various locations in Europe, and demand steadily increased. As a result, the company determined that shipping items to the United States, assembling the products, and then turning around and shipping them to Europe was inefficient and not cost effective. The company now plans to open three new distribution centers near ports in Europe, and it will ship its items from Asian ports to distribution centers at the European ports, offload some of the items for final product assembly, and then ship the partially filled containers on to the U.S. distribution centers. The following table shows the seven possible locations near container ports in Europe, and their container capacity that Pinnacle has identified to construct its proposed three distribution centers; the container shipments from each of its Asian ports; and the container shipping cost from each of the Asian ports to each possible distribution center location.
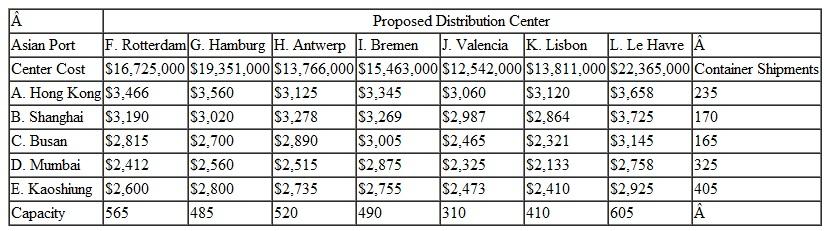 The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
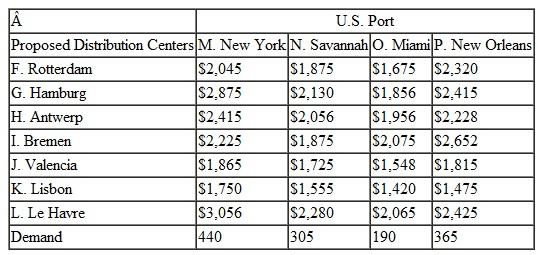 Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
 The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports: Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
25
The Vanguard Publishing Company wants to hire seven of the eight college students who have applied as salespeople to sell encyclopedias during the summer. The company desires to allocate them to three sales territories. Territory 1 requires three salespeople, and territories 2 and 3 require two salespeople each. It is estimated that each salesperson will be able to generate the amounts of dollar sales per day in each of the three territories as given in the following table:
 Help the company allocate the salespeople to the three territories so that sales will be maximized.
Help the company allocate the salespeople to the three territories so that sales will be maximized.
 Help the company allocate the salespeople to the three territories so that sales will be maximized.
Help the company allocate the salespeople to the three territories so that sales will be maximized.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
26
The Graphic Palette is a firm in Charleston, South Carolina, that does graphic artwork and produces color and black-and-white posters, lithographs, and banners. The firm's owners, Kathleen and Lindsey Taylor, have been approached by a client to produce a spectacularly colored poster for an upcoming arts festival. The poster is more complex than anything Kathleen and Lindsey have previously worked on. It requires color screening in three stages, and the processing must proceed rapidly to produce the desired color effect.
By suspending all their other jobs, they can devote three machines to the first stage, four to the second stage, and two to the last stage of the process. Posters that come off the machines at each stage can be processed on any of the machines at the next stage. However, all the machines are of different models and of varying ages, so they cannot process the same number of posters in the specified time frame necessary to complete the job. The different machine capacities at each stage are as follows:
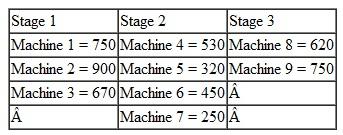 Because the machines are of different ages and types, the costs of producing posters on them differ. For example, a poster that starts on machine 1 and then proceeds to machine 4 costs $18. If this poster at machine 4 is then processed on machine 8, it costs an additional $36. The processing costs for each combination of machines for stages 1, 2, and 3 are as follows:
Because the machines are of different ages and types, the costs of producing posters on them differ. For example, a poster that starts on machine 1 and then proceeds to machine 4 costs $18. If this poster at machine 4 is then processed on machine 8, it costs an additional $36. The processing costs for each combination of machines for stages 1, 2, and 3 are as follows:
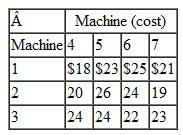
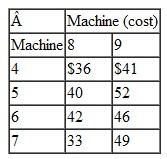 Kathleen and Lindsey are unsure how to route the posters from one stage to the next to make as many posters as they possibly can at the lowest cost. Determine how to route the posters through the various stages for Graphic Palette to minimize costs.
Kathleen and Lindsey are unsure how to route the posters from one stage to the next to make as many posters as they possibly can at the lowest cost. Determine how to route the posters through the various stages for Graphic Palette to minimize costs.
By suspending all their other jobs, they can devote three machines to the first stage, four to the second stage, and two to the last stage of the process. Posters that come off the machines at each stage can be processed on any of the machines at the next stage. However, all the machines are of different models and of varying ages, so they cannot process the same number of posters in the specified time frame necessary to complete the job. The different machine capacities at each stage are as follows:
 Because the machines are of different ages and types, the costs of producing posters on them differ. For example, a poster that starts on machine 1 and then proceeds to machine 4 costs $18. If this poster at machine 4 is then processed on machine 8, it costs an additional $36. The processing costs for each combination of machines for stages 1, 2, and 3 are as follows:
Because the machines are of different ages and types, the costs of producing posters on them differ. For example, a poster that starts on machine 1 and then proceeds to machine 4 costs $18. If this poster at machine 4 is then processed on machine 8, it costs an additional $36. The processing costs for each combination of machines for stages 1, 2, and 3 are as follows:
 Kathleen and Lindsey are unsure how to route the posters from one stage to the next to make as many posters as they possibly can at the lowest cost. Determine how to route the posters through the various stages for Graphic Palette to minimize costs.
Kathleen and Lindsey are unsure how to route the posters from one stage to the next to make as many posters as they possibly can at the lowest cost. Determine how to route the posters through the various stages for Graphic Palette to minimize costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
27
A severe winter ice storm has swept across North Carolina and Virginia, followed by over a foot of snow and frigid, single-digit temperatures. These weather conditions have resulted in numerous downed power lines and power outages, causing dangerous conditions for much of the population. Local utility companies have been overwhelmed and have requested assistance from unaffected utility companies across the Southeast. The following table shows the number of utility trucks with crews available from five different companies in Georgia, South Carolina, and Florida; the demand for crews in seven different areas that local companies cannot get to; and the weekly cost (in thousands of dollars) of a crew going to a specific area (based on the visiting company's normal charges, the distance the crew has to come, and living expenses in an area):
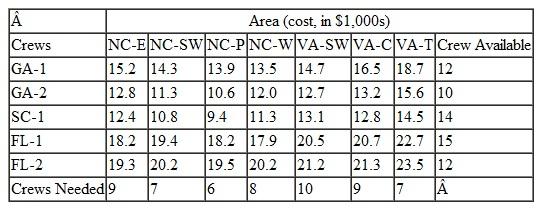 Determine the number of crews that should be sent from each utility to each affected area to minimize total costs.
Determine the number of crews that should be sent from each utility to each affected area to minimize total costs.
 Determine the number of crews that should be sent from each utility to each affected area to minimize total costs.
Determine the number of crews that should be sent from each utility to each affected area to minimize total costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
28
National Foods Company has five plants where it processes and packages fruits and vegetables. It has suppliers in six cities in California, Texas, Alabama, and Florida. The company owns and operates its own trucking system for transporting fruits and vegetables from its suppliers to its plants. However, it is now considering outsourcing all its shipping to outside trucking firms and getting rid of its own trucks. It currently spends $245,000 per month to operate its own trucking system. It has determined monthly shipping costs (in thousands of dollars per ton) of using outside shippers from each of its suppliers to each of its plants, as shown in the following table:
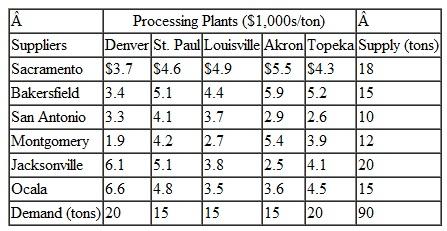 Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
 Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
29
In Problem, reformulate the model so that Pinnacle minimizes its shipping costs while selecting its three new distribution centers within a budget of $45 million. What is the difference in this solution, if any
Problem
The Pinnacle Company is a U.S.-based manufacturer of furniture and appliances that offshored all of its actual manufacturing operations to Asia about a decade ago. It then set up distribution centers at various locations on the East Coast, near ports where its items were imported on container ships. In many cases, Pinnacle's appliances and furniture arrive partially assembled, and the company completes the assembly at its distribution centers before sending the finished products to retailers. For example, appliance motors, electric controls, housings, and furniture pieces might arrive from different Asian manufacturers in separate containers. Recently Pinnacle began exporting its products to various locations in Europe, and demand steadily increased. As a result, the company determined that shipping items to the United States, assembling the products, and then turning around and shipping them to Europe was inefficient and not cost effective. The company now plans to open three new distribution centers near ports in Europe, and it will ship its items from Asian ports to distribution centers at the European ports, offload some of the items for final product assembly, and then ship the partially filled containers on to the U.S. distribution centers. The following table shows the seven possible locations near container ports in Europe, and their container capacity that Pinnacle has identified to construct its proposed three distribution centers; the container shipments from each of its Asian ports; and the container shipping cost from each of the Asian ports to each possible distribution center location.
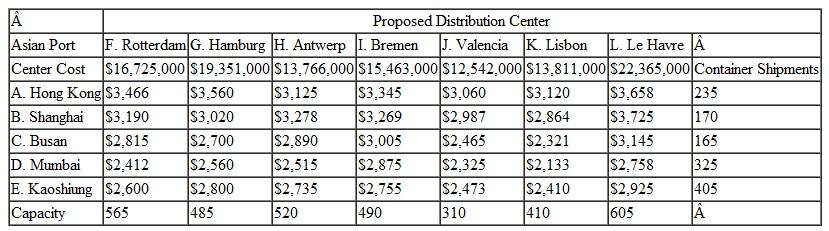 The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
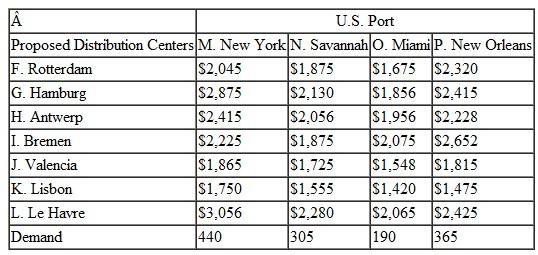 Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Problem
The Pinnacle Company is a U.S.-based manufacturer of furniture and appliances that offshored all of its actual manufacturing operations to Asia about a decade ago. It then set up distribution centers at various locations on the East Coast, near ports where its items were imported on container ships. In many cases, Pinnacle's appliances and furniture arrive partially assembled, and the company completes the assembly at its distribution centers before sending the finished products to retailers. For example, appliance motors, electric controls, housings, and furniture pieces might arrive from different Asian manufacturers in separate containers. Recently Pinnacle began exporting its products to various locations in Europe, and demand steadily increased. As a result, the company determined that shipping items to the United States, assembling the products, and then turning around and shipping them to Europe was inefficient and not cost effective. The company now plans to open three new distribution centers near ports in Europe, and it will ship its items from Asian ports to distribution centers at the European ports, offload some of the items for final product assembly, and then ship the partially filled containers on to the U.S. distribution centers. The following table shows the seven possible locations near container ports in Europe, and their container capacity that Pinnacle has identified to construct its proposed three distribution centers; the container shipments from each of its Asian ports; and the container shipping cost from each of the Asian ports to each possible distribution center location.
 The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports:
The following table shows the demand from each of the U.S. ports and the cost for container shipments from each of the possible distribution center locations to each of the U.S. ports: Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Formulate and solve a linear programming model to determine which three distribution center locations in Europe Pinnacle should select, and the shipments from each of the Asian ports to these selected distribution centers and from the European distribution centers to the U.S. ports.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
30
Carolina Airlines, a small commuter airline in North Carolina, has six flight attendants that it wants to assign to six monthly flight schedules in a way that will minimize the number of nights they will be away from their homes. The numbers of nights each attendant must be away from home with each schedule are given in the following table:
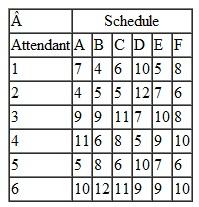 Identify the optimal assignments that will minimize the total number of nights the attendants will be away from home.
Identify the optimal assignments that will minimize the total number of nights the attendants will be away from home.
 Identify the optimal assignments that will minimize the total number of nights the attendants will be away from home.
Identify the optimal assignments that will minimize the total number of nights the attendants will be away from home.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
31
WeeMow Lawn Service provides lawn service, including mowing lawns and lawn care, landscaping, and lawn maintenance, to residential and commercial customers in the Draper town community. In the summer WeeMow has three teams that it schedules daily for jobs. Team 1 has five members, team 2 has four members, and team 3 has three members. On a normal summer day WeeMow will have approximately 14 jobs. Each team works 10 hours a day, but because of the heat plus work breaks, each team actually works only 45 minutes out of every hour. The following table shows the times (in minutes) and costs (in dollars) required for each team to complete the 14 jobs for a specific day.
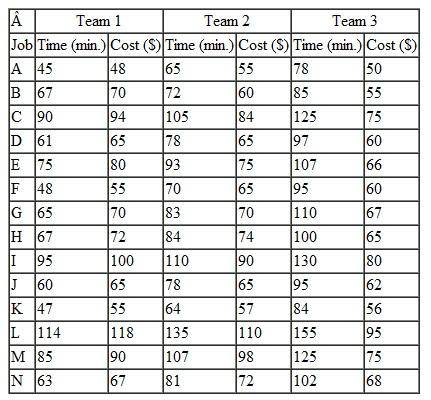 The WeeMow manager wants to develop a schedule of team assignments to the jobs for this day. Formulate and solve a linear programming model to determine the assignments of teams to jobs that will minimize total job time the day, given a daily budget of $1,000. Indicate how many minutes each crew will work during the day. Next, reformulate and solve this model if cost minimization is the objective. Of these two models, which one do you think the manger should select and why
The WeeMow manager wants to develop a schedule of team assignments to the jobs for this day. Formulate and solve a linear programming model to determine the assignments of teams to jobs that will minimize total job time the day, given a daily budget of $1,000. Indicate how many minutes each crew will work during the day. Next, reformulate and solve this model if cost minimization is the objective. Of these two models, which one do you think the manger should select and why
 The WeeMow manager wants to develop a schedule of team assignments to the jobs for this day. Formulate and solve a linear programming model to determine the assignments of teams to jobs that will minimize total job time the day, given a daily budget of $1,000. Indicate how many minutes each crew will work during the day. Next, reformulate and solve this model if cost minimization is the objective. Of these two models, which one do you think the manger should select and why
The WeeMow manager wants to develop a schedule of team assignments to the jobs for this day. Formulate and solve a linear programming model to determine the assignments of teams to jobs that will minimize total job time the day, given a daily budget of $1,000. Indicate how many minutes each crew will work during the day. Next, reformulate and solve this model if cost minimization is the objective. Of these two models, which one do you think the manger should select and why
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
32
A large manufacturing company is closing three of its existing plants and intends to transfer some of its more skilled employees to three plants that will remain open. The number of employees available for transfer from each closing plant is as follows:
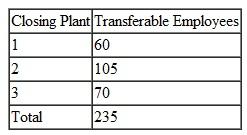 The following number of employees can be accommodated at the three plants remaining open:
The following number of employees can be accommodated at the three plants remaining open:
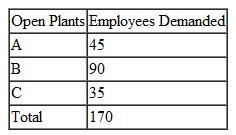 Each transferred employee will increase product output per day at each plant, as shown in the following table:
Each transferred employee will increase product output per day at each plant, as shown in the following table:
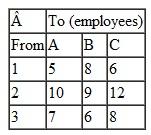 The company wants to transfer employees to ensure the maximum increase in product output. Solve this problem by using the computer.
The company wants to transfer employees to ensure the maximum increase in product output. Solve this problem by using the computer.
 The following number of employees can be accommodated at the three plants remaining open:
The following number of employees can be accommodated at the three plants remaining open: Each transferred employee will increase product output per day at each plant, as shown in the following table:
Each transferred employee will increase product output per day at each plant, as shown in the following table: The company wants to transfer employees to ensure the maximum increase in product output. Solve this problem by using the computer.
The company wants to transfer employees to ensure the maximum increase in product output. Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
33
In Problem, National Foods would like to know what the effect would be on the optimal solution and the company's decision regarding its shipping if it negotiates with its suppliers in Sacramento, Jacksonville, and Ocala to increase their capacity to 25 tons per month. What would be the effect of negotiating instead with its suppliers at San Antonio and Montgomery to increase their capacity to 25 tons each
Problem
National Foods Company has five plants where it processes and packages fruits and vegetables. It has suppliers in six cities in California, Texas, Alabama, and Florida. The company owns and operates its own trucking system for transporting fruits and vegetables from its suppliers to its plants. However, it is now considering outsourcing all its shipping to outside trucking firms and getting rid of its own trucks. It currently spends $245,000 per month to operate its own trucking system. It has determined monthly shipping costs (in thousands of dollars per ton) of using outside shippers from each of its suppliers to each of its plants, as shown in the following table:
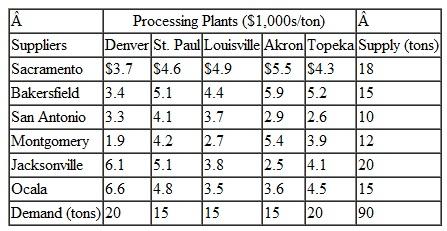 Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Problem
National Foods Company has five plants where it processes and packages fruits and vegetables. It has suppliers in six cities in California, Texas, Alabama, and Florida. The company owns and operates its own trucking system for transporting fruits and vegetables from its suppliers to its plants. However, it is now considering outsourcing all its shipping to outside trucking firms and getting rid of its own trucks. It currently spends $245,000 per month to operate its own trucking system. It has determined monthly shipping costs (in thousands of dollars per ton) of using outside shippers from each of its suppliers to each of its plants, as shown in the following table:
 Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Should National Foods continue to operate its own shipping network or sell its trucks and outsource its shipping to independent trucking firms
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
34
Formulate and solve a transshipment model for the shipments of cottons from the cotton processing facilities to the U.S. ports and to the overseas ports and Suntrek's fabric factories as described in Problems 1 and 2.
Problem 1
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
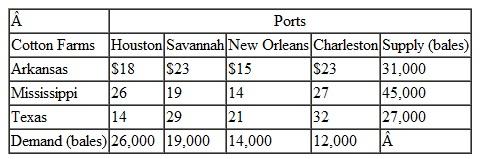 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Problem 2
Suntrek in Problem 3 ships the cotton it has purchased from the U.S. ports to overseas ports in Shanghai, Karachi, and Saigon, where its denim fabric factories are also located. The shipping and handling costs per bale of cotton from each U.S. port to each of Suntrek's overseas factories and the demand at these factories are as follows:
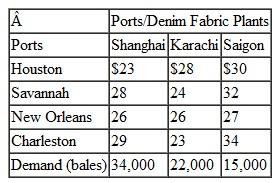 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.
Problem 3
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
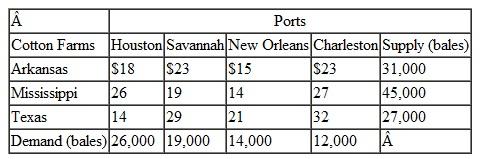 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Problem 1
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.Problem 2
Suntrek in Problem 3 ships the cotton it has purchased from the U.S. ports to overseas ports in Shanghai, Karachi, and Saigon, where its denim fabric factories are also located. The shipping and handling costs per bale of cotton from each U.S. port to each of Suntrek's overseas factories and the demand at these factories are as follows:
 Determine the optimal shipments that will result in the minimum total shipping cost.
Determine the optimal shipments that will result in the minimum total shipping cost.Problem 3
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
35
The football coaching staff at Tech focuses its recruiting on several key states, including Georgia, Florida, Virginia, Pennsylvania, New York, and New Jersey. The staff includes seven assistant coaches, two of whom are responsible for Florida, a high school talent-rich state, whereas one coach is assigned to each of the other five states. The staff has been together for a long time, and at one time or another all the coaches have recruited in all the states. The head coach has accumulated some data on the past success rate (i.e., percentage of targeted recruits signed) for each coach in each state, as shown in the following table:
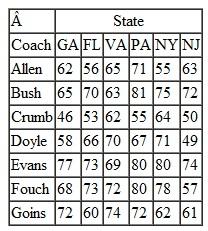 Determine the optimal assignment of coaches to recruiting regions that will maximize the overall success rate and indicate the average percentage success rate for the staff with this assignment.
Determine the optimal assignment of coaches to recruiting regions that will maximize the overall success rate and indicate the average percentage success rate for the staff with this assignment.
 Determine the optimal assignment of coaches to recruiting regions that will maximize the overall success rate and indicate the average percentage success rate for the staff with this assignment.
Determine the optimal assignment of coaches to recruiting regions that will maximize the overall success rate and indicate the average percentage success rate for the staff with this assignment.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the following transportation problem:
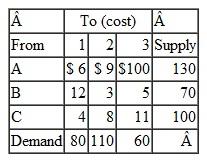 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
37
The Sav-Us Rental Car Agency has six lots in Nashville, and it wants to have a certain number of cars available at each lot at the beginning of each day for local rental. The agency would like a model it could quickly solve at the end of each day that would tell it how to redistribute the cars among the six lots in the minimum total time. The times required to travel between the six lots are as follows:
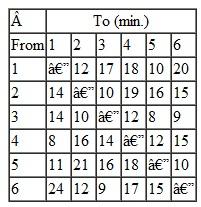 The agency would like the following number of cars at each lot at the end of the day. Also shown is the number of available cars at each lot at the end of a particular day. Determine the optimal reallocation of rental cars by using any initial solution approach and any solution method:
The agency would like the following number of cars at each lot at the end of the day. Also shown is the number of available cars at each lot at the end of a particular day. Determine the optimal reallocation of rental cars by using any initial solution approach and any solution method:
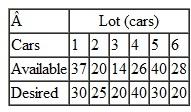
 The agency would like the following number of cars at each lot at the end of the day. Also shown is the number of available cars at each lot at the end of a particular day. Determine the optimal reallocation of rental cars by using any initial solution approach and any solution method:
The agency would like the following number of cars at each lot at the end of the day. Also shown is the number of available cars at each lot at the end of a particular day. Determine the optimal reallocation of rental cars by using any initial solution approach and any solution method:

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
38
Orient Express is a global distribution company that transports its clients' products to customers in Hong Kong, Singapore, and Taipei. All the products Orient Express ships are stored at three distribution centers-one in Los Angeles, one in Savannah, and one in Galveston. For the coming month the company has 450 containers of computer components available at the Los Angeles center, 600 containers available at Savannah, and 350 containers available at Galveston. The company has orders for 600 containers from Hong Kong, 500 containers from Singapore, and 500 containers from Taipei. The shipping costs per container from each U.S. port to each of the overseas ports are shown in the following table:
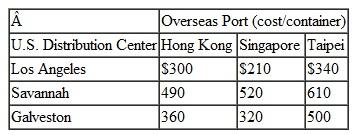 Orient Express, as the overseas broker for its U.S. customers, is responsible for unfulfilled orders, and it incurs stiff penalty costs from overseas customers if it does not meet an order. The Hong Kong customers charge a penalty cost of $800 per container for unfulfilled demand, Singapore customers charge a penalty cost of $920 per container, and Taipei customers charge $1,100 per container. Formulate and solve a transportation model to determine the shipments from each U.S. distribution center to each overseas port that will minimize shipping costs. Indicate what portion of the total cost is a result of penalties.
Orient Express, as the overseas broker for its U.S. customers, is responsible for unfulfilled orders, and it incurs stiff penalty costs from overseas customers if it does not meet an order. The Hong Kong customers charge a penalty cost of $800 per container for unfulfilled demand, Singapore customers charge a penalty cost of $920 per container, and Taipei customers charge $1,100 per container. Formulate and solve a transportation model to determine the shipments from each U.S. distribution center to each overseas port that will minimize shipping costs. Indicate what portion of the total cost is a result of penalties.
 Orient Express, as the overseas broker for its U.S. customers, is responsible for unfulfilled orders, and it incurs stiff penalty costs from overseas customers if it does not meet an order. The Hong Kong customers charge a penalty cost of $800 per container for unfulfilled demand, Singapore customers charge a penalty cost of $920 per container, and Taipei customers charge $1,100 per container. Formulate and solve a transportation model to determine the shipments from each U.S. distribution center to each overseas port that will minimize shipping costs. Indicate what portion of the total cost is a result of penalties.
Orient Express, as the overseas broker for its U.S. customers, is responsible for unfulfilled orders, and it incurs stiff penalty costs from overseas customers if it does not meet an order. The Hong Kong customers charge a penalty cost of $800 per container for unfulfilled demand, Singapore customers charge a penalty cost of $920 per container, and Taipei customers charge $1,100 per container. Formulate and solve a transportation model to determine the shipments from each U.S. distribution center to each overseas port that will minimize shipping costs. Indicate what portion of the total cost is a result of penalties.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
39
A plant has four operators to be assigned to four machines. The time (minutes) required by each worker to produce a product on each machine is shown in the following table:
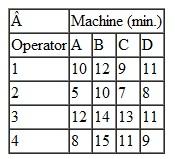 Determine the optimal assignment and compute total minimum time.
Determine the optimal assignment and compute total minimum time.
 Determine the optimal assignment and compute total minimum time.
Determine the optimal assignment and compute total minimum time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
40
Kathleen Taylor is a freshman at Roanoke College, and she wants to develop her schedule for the spring semester. Courses are offered with class periods either on Monday and Wednesday or Tuesday and Thursday for 1 hour and 15 minutes duration, with 15 minutes between class periods. For example, a course designated as 8M meets on Monday and Wednesday from 8:00 a.m. to 9:15 a.m.; the next class on Monday and Wednesday (9M) meets from 9:30 a.m. to 10:45 a.m.; the next class (11M) is from 11:00 a.m. to 12:15 p.m.; and so on. Kathleen wants to take the following six freshman courses, with the available sections shown in order of her preference, based on the professor who's teaching the course and the time:
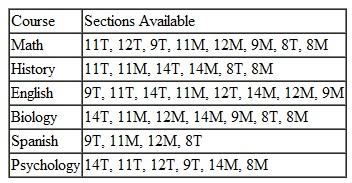 For example, there are eight sections of math offered, and Kathleen's first preference is the 11T section, her second choice is the 12T section, and so forth.
For example, there are eight sections of math offered, and Kathleen's first preference is the 11T section, her second choice is the 12T section, and so forth.
a. Determine a class schedule for Kathleen that most closely meets her preferences.
b. Determine a class schedule for Kathleen if she wants to leave 11:00 a.m. to noon open for lunch every day.
c. Suppose Kathleen wants all her classes on two days, either Monday and Wednesday or Tuesday and Thursday. Determine schedules for each and indicate which most closely matches her preferences.
 For example, there are eight sections of math offered, and Kathleen's first preference is the 11T section, her second choice is the 12T section, and so forth.
For example, there are eight sections of math offered, and Kathleen's first preference is the 11T section, her second choice is the 12T section, and so forth.a. Determine a class schedule for Kathleen that most closely meets her preferences.
b. Determine a class schedule for Kathleen if she wants to leave 11:00 a.m. to noon open for lunch every day.
c. Suppose Kathleen wants all her classes on two days, either Monday and Wednesday or Tuesday and Thursday. Determine schedules for each and indicate which most closely matches her preferences.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the following linear programming problem:
minimize Z = 3 x 11 + 12 x 12 + 8 x 13 + 10 x 21 + 5 x 22 + 6 x 23 + 6 x 31 + 7 x 32 + 10 x 33 subject to
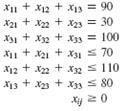
minimize Z = 3 x 11 + 12 x 12 + 8 x 13 + 10 x 21 + 5 x 22 + 6 x 23 + 6 x 31 + 7 x 32 + 10 x 33 subject to
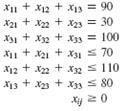

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
42
Bayville has built a new elementary school, increasing the town's total to four schools-Addison, Beeks, Canfield, and Daley. Each has a capacity of 400 students. The school board wants to assign children to schools so that their travel time by bus is as short as possible. The school board has partitioned the town into five districts conforming to population density-north, south, east, west, and central. The average bus travel time from each district to each school is shown as follows:
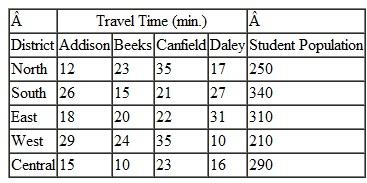 Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
 Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
43
Binford Tools manufactures garden tools. It uses inventory, overtime, and subcontracting to absorb demand fluctuations. Expected demand, regular and overtime production capacity, and subcontracting capacity are provided in the following table for the next four quarters for its basic line of steel garden tools:
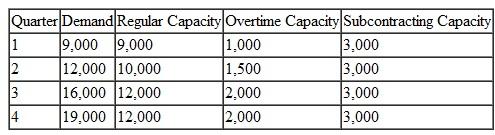 The regular production cost per unit is $20, the overtime cost per unit is $25, the cost to subcontract a unit is $27, and the inventory carrying cost is $2 per unit. The company has 300 units in inventory at the beginning of the year.
The regular production cost per unit is $20, the overtime cost per unit is $25, the cost to subcontract a unit is $27, and the inventory carrying cost is $2 per unit. The company has 300 units in inventory at the beginning of the year.
Determine the optimal production schedule for the four quarters to minimize total costs.
 The regular production cost per unit is $20, the overtime cost per unit is $25, the cost to subcontract a unit is $27, and the inventory carrying cost is $2 per unit. The company has 300 units in inventory at the beginning of the year.
The regular production cost per unit is $20, the overtime cost per unit is $25, the cost to subcontract a unit is $27, and the inventory carrying cost is $2 per unit. The company has 300 units in inventory at the beginning of the year.Determine the optimal production schedule for the four quarters to minimize total costs.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
44
A shop has four machinists to be assigned to four machines. The hourly cost of having each machine operated by each machinist is as follows:
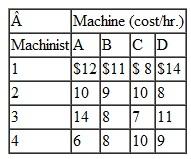 However, because he does not have enough experience, machinist 3 cannot operate machine B.
However, because he does not have enough experience, machinist 3 cannot operate machine B.
a. Determine the optimal assignment and compute total minimum cost.
b. Formulate this problem as a general linear programming model.
 However, because he does not have enough experience, machinist 3 cannot operate machine B.
However, because he does not have enough experience, machinist 3 cannot operate machine B.a. Determine the optimal assignment and compute total minimum cost.
b. Formulate this problem as a general linear programming model.

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
45
CareMed, an HMO health care provider, operates a 24-hour outpatient clinic in Draperton, near the Tech campus. The facility has a medical staff with doctors and nurses who see regular local patients according to a daily appointment schedule. However, the clinic sees a number of Tech students who visit the clinic each day and evening without appointments because their families are part of the CareMed network. The clinic has 12 nurses who work according to three 8-hour shifts. Five nurses are needed from 8:00 a.m. to 4:00 p.m., four nurses work from 4:00 p.m. to midnight, and 3 nurses work overnight from midnight to 8:00 a.m. The clinic administrator wants to assign nurses to a shift according to their preferences and seniority (i.e., when the number of nurses who prefer a shift exceeds the shift demand, the nurses are assigned according to seniority). While the majority of nurses prefer the day shift, some prefer other shifts because of the work and school schedules of their spouses and families. Following are the nurses' shift preferences (where 1 is most preferred) and their years working at the clinic:
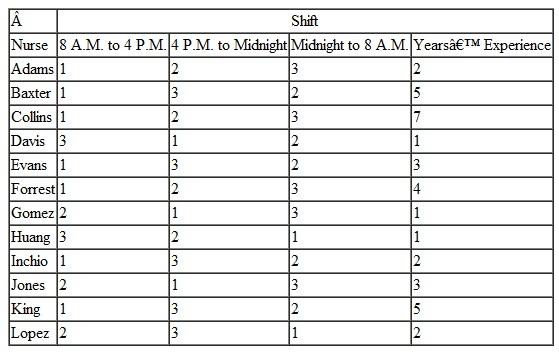 Formulate and solve a linear programming model to assign the nurses to shifts according to their preferences and seniority.
Formulate and solve a linear programming model to assign the nurses to shifts according to their preferences and seniority.
 Formulate and solve a linear programming model to assign the nurses to shifts according to their preferences and seniority.
Formulate and solve a linear programming model to assign the nurses to shifts according to their preferences and seniority.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the following transportation problem:
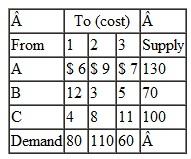 Solve it by using the computer.
Solve it by using the computer.
 Solve it by using the computer.
Solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
47
In Problem, the school board determined that it does not want any of the schools to be overly crowded compared with the other schools. It would like to assign students from each district to each school so that enrollments are evenly balanced between the four schools. However, the school board is concerned that this might significantly increase travel time. Determine the number of students to be assigned from each district to each school such that school enrollments are evenly balanced. Does this new solution appear to significantly increase travel time per student
Problem
Bayville has built a new elementary school, increasing the town's total to four schools-Addison, Beeks, Canfield, and Daley. Each has a capacity of 400 students. The school board wants to assign children to schools so that their travel time by bus is as short as possible. The school board has partitioned the town into five districts conforming to population density-north, south, east, west, and central. The average bus travel time from each district to each school is shown as follows:
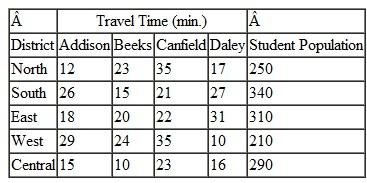 Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Problem
Bayville has built a new elementary school, increasing the town's total to four schools-Addison, Beeks, Canfield, and Daley. Each has a capacity of 400 students. The school board wants to assign children to schools so that their travel time by bus is as short as possible. The school board has partitioned the town into five districts conforming to population density-north, south, east, west, and central. The average bus travel time from each district to each school is shown as follows:
 Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Determine the number of children that should be assigned from each district to each school to minimize total student travel time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
48
The National Western Railroad's rail network covers most of the U.S. West and Midwest. On a daily basis it sends empty freight cars from various locations in its rail network to its customers for their use. Sometimes there are not enough freight cars to meet customer demand. The transportation costs for shipping empty freight cars, shown as follows, are directly related to distance traveled and the number of rail centers that must handle the car movement.
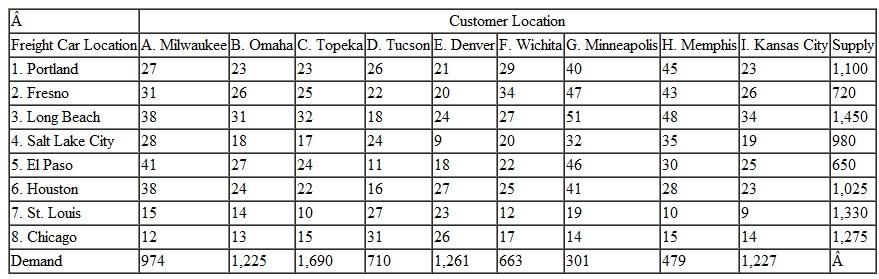 Determine the number of empty freight cars that should be sent from each rail network location to customers to meet demand at the minimum total cost.
Determine the number of empty freight cars that should be sent from each rail network location to customers to meet demand at the minimum total cost.
 Determine the number of empty freight cars that should be sent from each rail network location to customers to meet demand at the minimum total cost.
Determine the number of empty freight cars that should be sent from each rail network location to customers to meet demand at the minimum total cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
49
The Omega pharmaceutical firm has five salespersons, whom the firm wants to assign to five sales regions. Given their various previous contacts, the salespersons are able to cover the regions in different amounts of time. The amount of time (days) required by each salesperson to cover each city is shown in the following table:
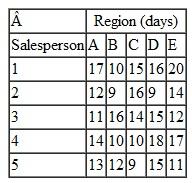 Which salesperson should be assigned to each region to minimize total time Identify the optimal assignments and compute total minimum time.
Which salesperson should be assigned to each region to minimize total time Identify the optimal assignments and compute total minimum time.
 Which salesperson should be assigned to each region to minimize total time Identify the optimal assignments and compute total minimum time.
Which salesperson should be assigned to each region to minimize total time Identify the optimal assignments and compute total minimum time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
50
The MidSouth Trucking Company based in Nashville has eight trucks located throughout the East and Midwest that have delivered their loads and are available for shipments. Through their Internet logistics site MidSouth has received shipping requests from 12 customers. The following table shows the mileage for a truck to travel to a customer location, pick up the load, and deliver it.
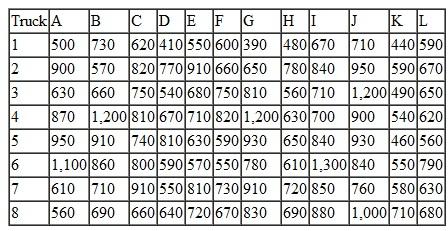 Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Determine the optimal assignment of trucks to customers that will minimize the total mileage.
 Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
51
Steel mills in three cities produce the following amounts of steel:
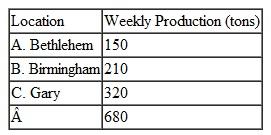 These mills supply steel to four cities, where manufacturing plants have the following demand:
These mills supply steel to four cities, where manufacturing plants have the following demand:
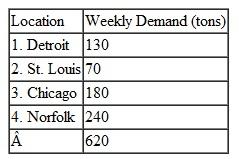 Shipping costs per ton of steel are as follows:
Shipping costs per ton of steel are as follows:
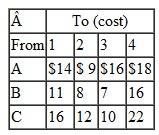 Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
 These mills supply steel to four cities, where manufacturing plants have the following demand:
These mills supply steel to four cities, where manufacturing plants have the following demand: Shipping costs per ton of steel are as follows:
Shipping costs per ton of steel are as follows: Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
52
The Easy Time Grocery chain operates in major metropolitan areas on the East Coast. The stores have a "no-frills" approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food, based on where the chain purchases it and at which store it is sold, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week:
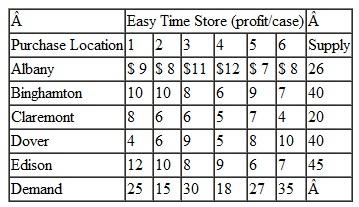 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
53
Al, Barbara, Carol, and Dave have joined together to purchase two season tickets to the Giants' home football games. Because there are eight home games, each person will get tickets to two games. Each person has ranked the games they prefer from 1 to 8, with 1 being most preferred and 8 least preferred, as follows:
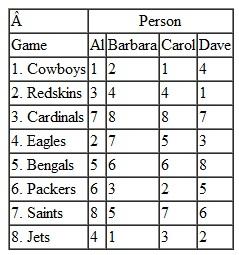 Determine the two games each person should get tickets for that will result in the groups' greatest degree of satisfaction. Do you think the participants will think your allocation is fair
Determine the two games each person should get tickets for that will result in the groups' greatest degree of satisfaction. Do you think the participants will think your allocation is fair
 Determine the two games each person should get tickets for that will result in the groups' greatest degree of satisfaction. Do you think the participants will think your allocation is fair
Determine the two games each person should get tickets for that will result in the groups' greatest degree of satisfaction. Do you think the participants will think your allocation is fair
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
54
The Bunker Manufacturing firm has five employees and six machines and wants to assign the employees to the machines to minimize cost. A cost table showing the cost incurred by each employee on each machine follows:
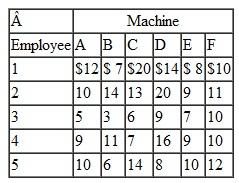 Because of union rules regarding departmental transfers, employee 3 cannot be assigned to machine E, and employee 4 cannot be assigned to machine B. Solve this problem, indicate the optimal assignment, and compute total minimum cost.
Because of union rules regarding departmental transfers, employee 3 cannot be assigned to machine E, and employee 4 cannot be assigned to machine B. Solve this problem, indicate the optimal assignment, and compute total minimum cost.
 Because of union rules regarding departmental transfers, employee 3 cannot be assigned to machine E, and employee 4 cannot be assigned to machine B. Solve this problem, indicate the optimal assignment, and compute total minimum cost.
Because of union rules regarding departmental transfers, employee 3 cannot be assigned to machine E, and employee 4 cannot be assigned to machine B. Solve this problem, indicate the optimal assignment, and compute total minimum cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
55
In Problem, assume that the customers have the following truck capacity percentage loads:
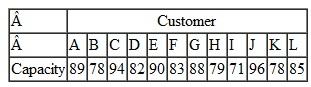 Determine the optimal assignment of trucks to customers that will minimize total mileage while also achieving at least an average truck load capacity of 85%. Does this load capacity requirement significantly increase the total mileage
Determine the optimal assignment of trucks to customers that will minimize total mileage while also achieving at least an average truck load capacity of 85%. Does this load capacity requirement significantly increase the total mileage
Problem
The MidSouth Trucking Company based in Nashville has eight trucks located throughout the East and Midwest that have delivered their loads and are available for shipments. Through their Internet logistics site MidSouth has received shipping requests from 12 customers. The following table shows the mileage for a truck to travel to a customer location, pick up the load, and deliver it.
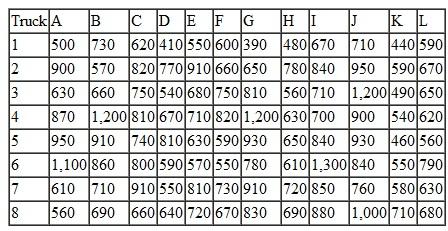 Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Determine the optimal assignment of trucks to customers that will minimize the total mileage.
 Determine the optimal assignment of trucks to customers that will minimize total mileage while also achieving at least an average truck load capacity of 85%. Does this load capacity requirement significantly increase the total mileage
Determine the optimal assignment of trucks to customers that will minimize total mileage while also achieving at least an average truck load capacity of 85%. Does this load capacity requirement significantly increase the total mileageProblem
The MidSouth Trucking Company based in Nashville has eight trucks located throughout the East and Midwest that have delivered their loads and are available for shipments. Through their Internet logistics site MidSouth has received shipping requests from 12 customers. The following table shows the mileage for a truck to travel to a customer location, pick up the load, and deliver it.
 Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Determine the optimal assignment of trucks to customers that will minimize the total mileage.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
56
In Problem, what would be the effect on the optimal solution of a reduction in production capacity at the Gary mill from 320 tons to 290 tons per week
Problem
Steel mills in three cities produce the following amounts of steel:
 These mills supply steel to four cities, where manufacturing plants have the following demand:
These mills supply steel to four cities, where manufacturing plants have the following demand:
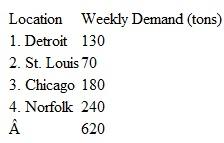 Shipping costs per ton of steel are as follows:
Shipping costs per ton of steel are as follows:
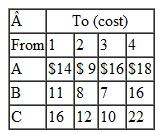 Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Problem
Steel mills in three cities produce the following amounts of steel:
 These mills supply steel to four cities, where manufacturing plants have the following demand:
These mills supply steel to four cities, where manufacturing plants have the following demand: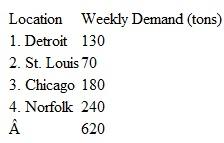 Shipping costs per ton of steel are as follows:
Shipping costs per ton of steel are as follows: Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Because of a truckers' strike, shipments are prohibited from Birmingham to Chicago. Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose that in Problem Easy Time can purchase all the baby food it needs from a New York City distributor at a price that will result in a profit of $9 per case at stores 1, 3, and 4; $8 per case at stores 2 and 6; and $7 per case at store 5. Should Easy Time purchase all, none, or some of its baby food from the distributor rather than purchase it at other stores and truck it in
Problem
The Easy Time Grocery chain operates in major metropolitan areas on the East Coast. The stores have a "no-frills" approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food, based on where the chain purchases it and at which store it is sold, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week:
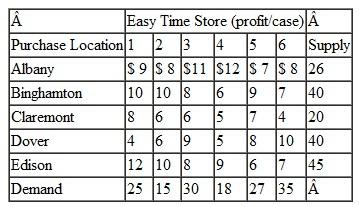 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Problem
The Easy Time Grocery chain operates in major metropolitan areas on the East Coast. The stores have a "no-frills" approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food, based on where the chain purchases it and at which store it is sold, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week:
 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
58
World Foods, Inc., imports food products such as meats, cheese, and pastries to the United States from warehouses at ports in Hamburg, Marseilles, and Liverpool. Ships from these ports deliver the products to Norfolk, New York, and Savannah, where they are stored in company warehouses before being shipped to distribution centers in Dallas, St. Louis, and Chicago. The products are then distributed to specialty food stores and sold through catalogs. The shipping costs ($/1,000 lb.) from the European ports to the U.S. cities and the available supplies (1,000 lb.) at the European ports are provided in the following table:
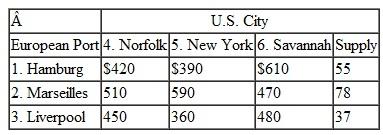 The transportation costs ($/1,000 lb.) from each U.S. city of the three distribution centers and the demands (1,000 lb.) at the distribution centers are as follows:
The transportation costs ($/1,000 lb.) from each U.S. city of the three distribution centers and the demands (1,000 lb.) at the distribution centers are as follows:
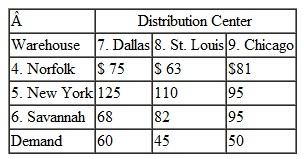 Determine the optimal shipments between the European ports and the warehouses and the distribution centers to minimize total transportation costs.
Determine the optimal shipments between the European ports and the warehouses and the distribution centers to minimize total transportation costs.
 The transportation costs ($/1,000 lb.) from each U.S. city of the three distribution centers and the demands (1,000 lb.) at the distribution centers are as follows:
The transportation costs ($/1,000 lb.) from each U.S. city of the three distribution centers and the demands (1,000 lb.) at the distribution centers are as follows: Determine the optimal shipments between the European ports and the warehouses and the distribution centers to minimize total transportation costs.
Determine the optimal shipments between the European ports and the warehouses and the distribution centers to minimize total transportation costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
59
Given the following cost table for an assignment problem, determine the optimal assignment and compute total minimum cost:
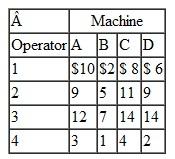


Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
60
The Hilton Island Tennis Club is hosting its annual professional tennis tournament. One of the tournament committee's scheduling activities is to assign chair umpires to the various matches. The tennis association rates chair umpires from 1 (best) to worst (4) based on experience, consistency, and player and coach evaluations. On a particular afternoon 12 matches start at 1:00 P.M. Fifteen chair umpires are available to officiate the matches. The matches are prioritized from 1 to 12 in order of importance, based on the rankings and seedings of the players involved, and whether it is a singles or a doubles match. The committee wants to assign the best umpires to the highest priority matches. The following tables show the match priorities and the umpire ratings.
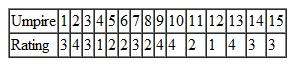
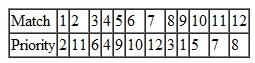 Determine the optimal assignment of umpires to matches.
Determine the optimal assignment of umpires to matches.

 Determine the optimal assignment of umpires to matches.
Determine the optimal assignment of umpires to matches.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
61
Coal is mined and processed at the following four mines in Kentucky, West Virginia, and Virginia:
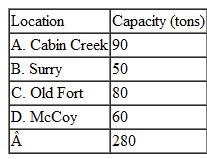 These mines supply the following amount of coal to utility power plants in three cities:
These mines supply the following amount of coal to utility power plants in three cities:
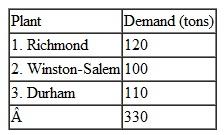 The railroad shipping costs (in thousands of dollars) per ton of coal are shown in the following table. Because of railroad construction, shipments are prohibited from Cabin Creek to Richmond:
The railroad shipping costs (in thousands of dollars) per ton of coal are shown in the following table. Because of railroad construction, shipments are prohibited from Cabin Creek to Richmond:
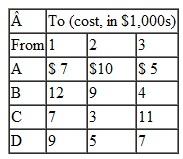 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
 These mines supply the following amount of coal to utility power plants in three cities:
These mines supply the following amount of coal to utility power plants in three cities: The railroad shipping costs (in thousands of dollars) per ton of coal are shown in the following table. Because of railroad construction, shipments are prohibited from Cabin Creek to Richmond:
The railroad shipping costs (in thousands of dollars) per ton of coal are shown in the following table. Because of railroad construction, shipments are prohibited from Cabin Creek to Richmond: Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
62
In Problem, if Easy Time could arrange to purchase more baby food from one of the outlying locations, which should it be, how many additional cases could be purchased, and how much would this increase profit
Problem
The Easy Time Grocery chain operates in major metropolitan areas on the East Coast. The stores have a "no-frills" approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food, based on where the chain purchases it and at which store it is sold, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week:
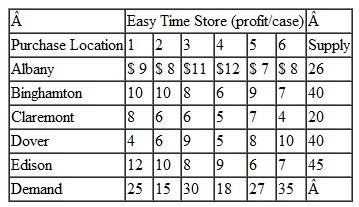 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Problem
The Easy Time Grocery chain operates in major metropolitan areas on the East Coast. The stores have a "no-frills" approach, with low overhead and high volume. They generally buy their stock in volume at low prices. However, in some cases they actually buy stock at stores in other areas and ship it in. They can do this because of high prices in the cities they operate in compared with costs in other locations. One example is baby food. Easy Time purchases baby food at stores in Albany, Binghamton, Claremont, Dover, and Edison and then trucks it to six stores in and around New York City. The stores in the outlying areas know what Easy Time is up to, so they limit the number of cases of baby food Easy Time can purchase. The following table shows the profit Easy Time makes per case of baby food, based on where the chain purchases it and at which store it is sold, plus the available baby food per week at purchase locations and the shelf space available at each Easy Time store per week:
 Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Determine where Easy Time should purchase baby food and how the food should be distributed to maximize profit.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
63
A sports apparel company has received an order for a college basketball team's national championship T-shirt. The company can purchase the T-shirts from textile factories in Mexico, Puerto Rico, and Haiti. The shirts are shipped from the factories to companies in the United States that silk-screen the shirts before they are shipped to distribution centers. Following are the production and transportation costs ($/shirt) from the T-shirt factories to the silk-screen companies to the distribution centers, plus the supply of T-shirts at the factories and demand for the shirts at the distribution centers:
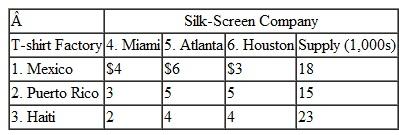
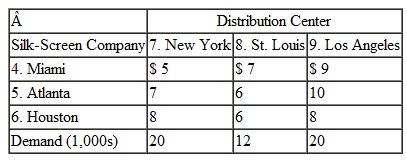 Determine the optimal shipments to minimize total production and transportation costs for the apparel company.
Determine the optimal shipments to minimize total production and transportation costs for the apparel company.

 Determine the optimal shipments to minimize total production and transportation costs for the apparel company.
Determine the optimal shipments to minimize total production and transportation costs for the apparel company.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
64
An electronics firm produces electronic components, which it supplies to various electrical manufacturers. Quality control records indicate that different employees produce different numbers of defective items. The average number of defects produced by each employee for each of six components is given in the following table:
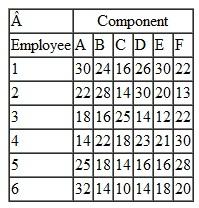 Determine the optimal assignment that will minimize the total average number of defects produced by the firm per month.
Determine the optimal assignment that will minimize the total average number of defects produced by the firm per month.
 Determine the optimal assignment that will minimize the total average number of defects produced by the firm per month.
Determine the optimal assignment that will minimize the total average number of defects produced by the firm per month.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
65
The National Collegiate Lacrosse Association is planning its annual national championship tournament. It selects 16 teams from conference champions and the highest ranked at-large teams to play in the single-elimination tournament. The teams are ranked from 1 (best) to 16 (worst), and in the first round of the tournament, the association wants to pair the teams so that highranked teams play low-ranked teams (i.e., seed them so that 1 plays 16, 2 plays 15, etc.). The eight first-round game sites are predetermined and have been selected based on stadium size and conditions, as well as historical local fan interest in lacrosse. Because of limited school budgets for lacrosse and a desire to boost game attendance, the association wants to assign teams to game sites so that all schools will have to travel the least amount possible. The following table shows the 16 teams in order of their ranking and the distance (in miles) for each of the teams to each of the eight game sites.
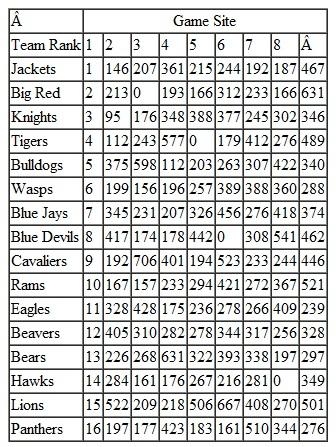 Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
 Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
66
Oranges are grown, picked, and then stored in warehouses in Tampa, Miami, and Fresno. These warehouses supply oranges to markets in New York, Philadelphia, Chicago, and Boston. The following table shows the shipping costs per truckload (in hundreds of dollars), supply, and demand. Because of an agreement between distributors, shipments are prohibited from Miami to Chicago:
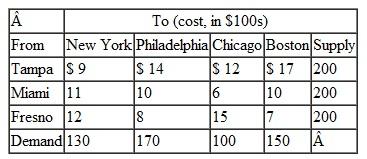 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
67
The Roadnet Transport Company expanded its shipping capacity by purchasing 90 trailer trucks from a competitor that went bankrupt. The company subsequently located 30 of the purchased trucks at each of its shipping warehouses in Charlotte, Memphis, and Louisville. The company makes shipments from each of these warehouses to terminals in St. Louis, Atlanta, and New York. Each truck is capable of making one shipment per week. The terminal managers have indicated their capacity of extra shipments. The manager at St. Louis can accommodate 40 additional trucks per week, the manager at Atlanta can accommodate 60 additional trucks, and the manager at New York can accommodate 50 additional trucks. The company makes the following profit per truckload shipment from each warehouse to each terminal. The profits differ as a result of differences in products shipped, shipping costs, and transport rates:
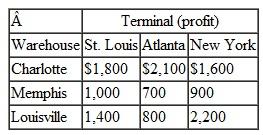 Determine how many trucks to assign to each route (i.e., warehouse to terminal) in order to maximize profit.
Determine how many trucks to assign to each route (i.e., warehouse to terminal) in order to maximize profit.
 Determine how many trucks to assign to each route (i.e., warehouse to terminal) in order to maximize profit.
Determine how many trucks to assign to each route (i.e., warehouse to terminal) in order to maximize profit.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
68
Walsh's Fruit Company contracts with growers in Ohio, Pennsylvania, and New York to purchase grapes. The grapes are processed into juice at the farms and stored in refrigerated vats. Then the juice is shipped to two plants, where it is processed into bottled grape juice and frozen concentrate. The juice and concentrate are then transported to three food warehouses/distribution centers. The transportation costs per ton from the farms to the plants and from the plants to the distributors, and the supply at the farms and demand at the distribution centers are summarized in the following tables:
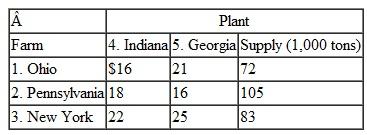
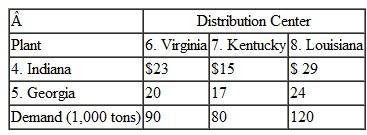 a. Determine the optimal shipments from farms to plants to distribution centers to minimize total transportation costs.
a. Determine the optimal shipments from farms to plants to distribution centers to minimize total transportation costs.
b. What would be the effect on the solution if the capacity at each plant were 140,000 tons

 a. Determine the optimal shipments from farms to plants to distribution centers to minimize total transportation costs.
a. Determine the optimal shipments from farms to plants to distribution centers to minimize total transportation costs.b. What would be the effect on the solution if the capacity at each plant were 140,000 tons

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
69
A dispatcher for Citywide Taxi Company has six taxicabs at different locations and five customers who have called for service. The mileage from each taxi's present location to each customer is shown in the following table:
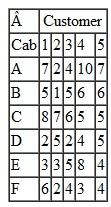 Determine the optimal assignment(s) that will minimize the total mileage traveled.
Determine the optimal assignment(s) that will minimize the total mileage traveled.
 Determine the optimal assignment(s) that will minimize the total mileage traveled.
Determine the optimal assignment(s) that will minimize the total mileage traveled.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
70
Suppose that in Problem, the association wants to consider allowing some flexibility in pairing the teams according to their rankings (i.e., seedings)-for example 1 might play 14 or 2 might play 12-in order to see to what extent overall team travel might be reduced. Reformulate and solve the model in order to see what effect this might have.
Problem
The National Collegiate Lacrosse Association is planning its annual national championship tournament. It selects 16 teams from conference champions and the highest ranked at-large teams to play in the single-elimination tournament. The teams are ranked from 1 (best) to 16 (worst), and in the first round of the tournament, the association wants to pair the teams so that highranked teams play low-ranked teams (i.e., seed them so that 1 plays 16, 2 plays 15, etc.). The eight first-round game sites are predetermined and have been selected based on stadium size and conditions, as well as historical local fan interest in lacrosse. Because of limited school budgets for lacrosse and a desire to boost game attendance, the association wants to assign teams to game sites so that all schools will have to travel the least amount possible. The following table shows the 16 teams in order of their ranking and the distance (in miles) for each of the teams to each of the eight game sites.
 Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Problem
The National Collegiate Lacrosse Association is planning its annual national championship tournament. It selects 16 teams from conference champions and the highest ranked at-large teams to play in the single-elimination tournament. The teams are ranked from 1 (best) to 16 (worst), and in the first round of the tournament, the association wants to pair the teams so that highranked teams play low-ranked teams (i.e., seed them so that 1 plays 16, 2 plays 15, etc.). The eight first-round game sites are predetermined and have been selected based on stadium size and conditions, as well as historical local fan interest in lacrosse. Because of limited school budgets for lacrosse and a desire to boost game attendance, the association wants to assign teams to game sites so that all schools will have to travel the least amount possible. The following table shows the 16 teams in order of their ranking and the distance (in miles) for each of the teams to each of the eight game sites.
 Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Formulate and solve a linear programming model that will assign the teams to the game sites according to the association's guidelines.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
71
Brenda Last is the personnel director at the Burlingham Textile Company. The company's plant is expanding, and Brenda must fill five new supervisory positions in carding, spinning, weaving, inspection, and shipping. Applicants for the positions are required to take a written psychological and aptitude test. The test has different modules that indicate an applicant's aptitude and suitability for a specific area and position. For example, one module tests the psychological traits and intellectual skills that are best suited for the inspection department, which are different from the traits and skills required in shipping. Brenda has had 10 applicants for the five positions and has compiled the results from the test. The test scores for each position module for each applicant (where the higher the score, the better) are as follows:
 Brenda wants to offer the vacant positions to the five most qualified candidates. Determine an optimal assignment for Brenda.
Brenda wants to offer the vacant positions to the five most qualified candidates. Determine an optimal assignment for Brenda.
There is a possibility that one or more of the successful applicants will turn down a position offer, and Brenda wants to be able to hire the next-best person into a position if someone rejects a job offer. If the applicant selected for the carding job turns it down, whom should Brenda offer this job to next If the applicants for both the carding and spinning jobs turn them down, which of the remaining applicants should Brenda offer each job to How would a third applicant be selected if three of the job offers were declined
Brenda believes this is a particularly good group of applicants. She would like to retain a few of the people for several more supervisory positions that she believes will open up soon. She has two vacant clerical positions that she can offer to the two best applicants not selected for the five original supervisory positions. Then when the supervisory positions open, she can move these people into them. How should Brenda identify these two people
 Brenda wants to offer the vacant positions to the five most qualified candidates. Determine an optimal assignment for Brenda.
Brenda wants to offer the vacant positions to the five most qualified candidates. Determine an optimal assignment for Brenda.There is a possibility that one or more of the successful applicants will turn down a position offer, and Brenda wants to be able to hire the next-best person into a position if someone rejects a job offer. If the applicant selected for the carding job turns it down, whom should Brenda offer this job to next If the applicants for both the carding and spinning jobs turn them down, which of the remaining applicants should Brenda offer each job to How would a third applicant be selected if three of the job offers were declined
Brenda believes this is a particularly good group of applicants. She would like to retain a few of the people for several more supervisory positions that she believes will open up soon. She has two vacant clerical positions that she can offer to the two best applicants not selected for the five original supervisory positions. Then when the supervisory positions open, she can move these people into them. How should Brenda identify these two people

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
72
A manufacturing firm produces diesel engines in four cities-Phoenix, Seattle, St. Louis, and Detroit. The company is able to produce the following numbers of engines per month:
 Three trucking firms purchase the following numbers of engines for their plants in three cities:
Three trucking firms purchase the following numbers of engines for their plants in three cities:
 The transportation costs per engine (in hundreds of dollars) from sources to destinations are shown in the following table. However, the Charlotte firm will not accept engines made in Seattle, and the Louisville firm will not accept engines from Detroit; therefore, those routes are prohibited:
The transportation costs per engine (in hundreds of dollars) from sources to destinations are shown in the following table. However, the Charlotte firm will not accept engines made in Seattle, and the Louisville firm will not accept engines from Detroit; therefore, those routes are prohibited:
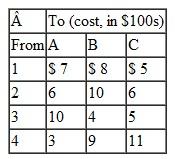 Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
 Three trucking firms purchase the following numbers of engines for their plants in three cities:
Three trucking firms purchase the following numbers of engines for their plants in three cities: The transportation costs per engine (in hundreds of dollars) from sources to destinations are shown in the following table. However, the Charlotte firm will not accept engines made in Seattle, and the Louisville firm will not accept engines from Detroit; therefore, those routes are prohibited:
The transportation costs per engine (in hundreds of dollars) from sources to destinations are shown in the following table. However, the Charlotte firm will not accept engines made in Seattle, and the Louisville firm will not accept engines from Detroit; therefore, those routes are prohibited: Formulate this problem as a linear programming model and solve it by using the computer.
Formulate this problem as a linear programming model and solve it by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
73
During U.S. military action in the Middle East, large amounts of military matériel and supplies had to be shipped daily from supply depots in the United States. The critical factor in the movement of these supplies was speed. The following table shows the number of planeloads of supplies available each day from each of six supply depots and the number of daily loads demanded at each of five bases in the Middle East. (Each planeload is approximately equal in tonnage.) Also included are the transport hours per plane, including loading and fueling, actual flight time, and unloading and refueling:
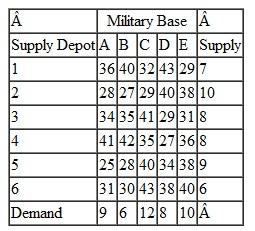 Determine the optimal daily flight schedule that will minimize total transport time.
Determine the optimal daily flight schedule that will minimize total transport time.
 Determine the optimal daily flight schedule that will minimize total transport time.
Determine the optimal daily flight schedule that will minimize total transport time.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
74
A national catalog and Internet retailer has three warehouses and three major distribution centers located around the country. Normally, items are shipped directly from the warehouses to the distribution centers; however, each of the distribution centers can also be used as an intermediate transshipment point. The transportation costs ($/unit) between warehouses and distribution centers, the supply at the warehouses (100 units), and the demand at the distribution centers (100 units) for a specific week are shown in the following table:
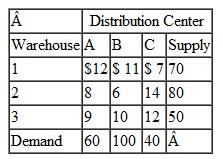 The transportation costs ($/unit) between the distribution centers are
The transportation costs ($/unit) between the distribution centers are
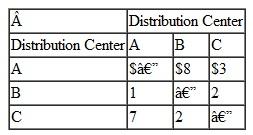 Determine the optimal shipments between warehouses and distribution centers to minimize total transportation costs.
Determine the optimal shipments between warehouses and distribution centers to minimize total transportation costs.
 The transportation costs ($/unit) between the distribution centers are
The transportation costs ($/unit) between the distribution centers are Determine the optimal shipments between warehouses and distribution centers to minimize total transportation costs.
Determine the optimal shipments between warehouses and distribution centers to minimize total transportation costs.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
75
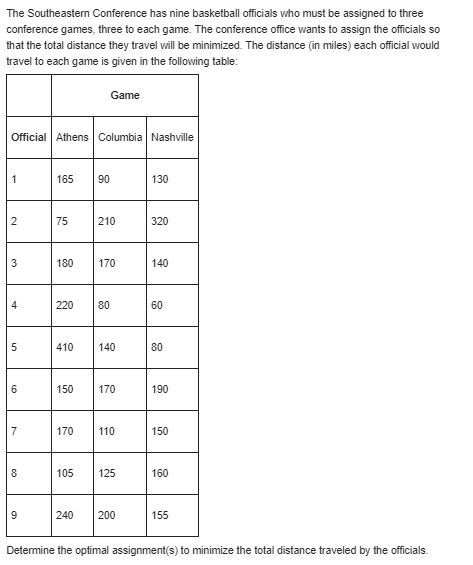

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
76
Erken Apparel International manufactures clothing items around the world. It has currently contracted with a U.S. retail clothing wholesale distributor for men's goatskin and lambskin leather jackets for the next Christmas season. The distributor has distribution centers in Indiana, North Carolina, and Pennsylvania. The distributor supplies the leather jackets to a discount retail chain, a chain of mall boutique stores, and a department store chain. The jackets arrive at the distribution centers unfinished, and at the centers the distributor adds a unique lining and label specific to each of its customers. The distributor has contracted with Erken to deliver the following number of leather jackets to its distribution centers in late fall:
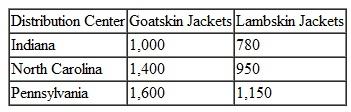 Erken has tanning factories and clothing manufacturing plants to produce leather jackets in Spain, France, Italy, Venezuela, and Brazil. Its tanning facilities are in Mende in France, Foggia in Italy, Saragosa in Spain, Feira in Brazil, and El Tigre in Venezuela. Its manufacturing plants are in Limoges, Naples, and Madrid in Europe and in Sao Paulo and Caracas in South America. Following are the supplies of available leather from each tanning facility and the processing capacity at each plant (in pounds) for this particular order of leather jackets:
Erken has tanning factories and clothing manufacturing plants to produce leather jackets in Spain, France, Italy, Venezuela, and Brazil. Its tanning facilities are in Mende in France, Foggia in Italy, Saragosa in Spain, Feira in Brazil, and El Tigre in Venezuela. Its manufacturing plants are in Limoges, Naples, and Madrid in Europe and in Sao Paulo and Caracas in South America. Following are the supplies of available leather from each tanning facility and the processing capacity at each plant (in pounds) for this particular order of leather jackets:
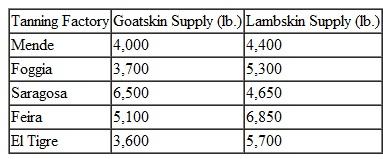
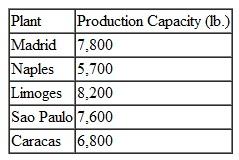 In the production of jackets at the plants, 37.5% of the goatskin leather and 50% of the lambskin leather is waste (i.e., it is discarded during the production process and sold for other byproducts). After production, a goatskin jacket weighs approximately 3 pounds, and a lambskin jacket weighs approximately 2.5 pounds (neither with linings, which are added in the United States).
In the production of jackets at the plants, 37.5% of the goatskin leather and 50% of the lambskin leather is waste (i.e., it is discarded during the production process and sold for other byproducts). After production, a goatskin jacket weighs approximately 3 pounds, and a lambskin jacket weighs approximately 2.5 pounds (neither with linings, which are added in the United States).
Following are the costs per pound, in U.S. dollars, for tanning the uncut leather, shipping it, and producing the leather jackets at each plant:
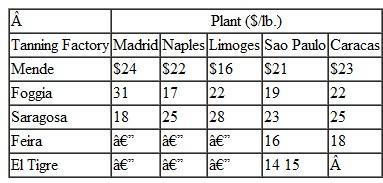 Note that the cost of jacket production is the same for goatskin and lambskin. Also, leather can be tanned in France, Spain, and Italy and shipped directly to the South American plants for jacket production, but the opposite is not possible due to high tariff restrictions (i.e., tanned leather is not shipped to Europe for production).
Note that the cost of jacket production is the same for goatskin and lambskin. Also, leather can be tanned in France, Spain, and Italy and shipped directly to the South American plants for jacket production, but the opposite is not possible due to high tariff restrictions (i.e., tanned leather is not shipped to Europe for production).
Once the leather jackets are produced at the plants in Europe and South America, Erken transports them to ports in Lisbon, Marseilles, and Caracas and then from these ports to U.S. ports in New Orleans, Jacksonville, and Savannah. The available shipping capacity at each port and the transportation costs from the plants to the ports are as follows:
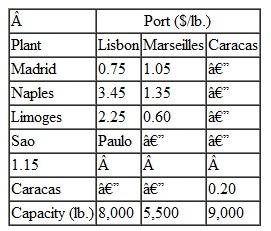 The shipping costs ($/lb.) from each port in Europe and South America to the U.S. ports and the available truck and rail capacity for transport at the U.S. ports are as follows:
The shipping costs ($/lb.) from each port in Europe and South America to the U.S. ports and the available truck and rail capacity for transport at the U.S. ports are as follows:
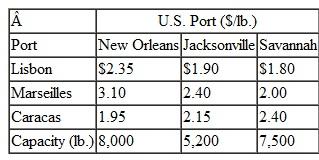 The transportation costs ($/lb.) from the U.S. ports to the three distribution centers are as follows:
The transportation costs ($/lb.) from the U.S. ports to the three distribution centers are as follows:
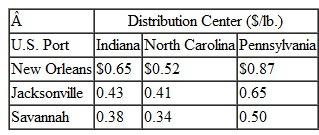 Erken wants to determine the least costly shipments of material and jackets that will meet the demand at the U.S. distribution centers. Develop a transshipment model for Erken that will result in a minimum cost solution.
Erken wants to determine the least costly shipments of material and jackets that will meet the demand at the U.S. distribution centers. Develop a transshipment model for Erken that will result in a minimum cost solution.
 Erken has tanning factories and clothing manufacturing plants to produce leather jackets in Spain, France, Italy, Venezuela, and Brazil. Its tanning facilities are in Mende in France, Foggia in Italy, Saragosa in Spain, Feira in Brazil, and El Tigre in Venezuela. Its manufacturing plants are in Limoges, Naples, and Madrid in Europe and in Sao Paulo and Caracas in South America. Following are the supplies of available leather from each tanning facility and the processing capacity at each plant (in pounds) for this particular order of leather jackets:
Erken has tanning factories and clothing manufacturing plants to produce leather jackets in Spain, France, Italy, Venezuela, and Brazil. Its tanning facilities are in Mende in France, Foggia in Italy, Saragosa in Spain, Feira in Brazil, and El Tigre in Venezuela. Its manufacturing plants are in Limoges, Naples, and Madrid in Europe and in Sao Paulo and Caracas in South America. Following are the supplies of available leather from each tanning facility and the processing capacity at each plant (in pounds) for this particular order of leather jackets:
 In the production of jackets at the plants, 37.5% of the goatskin leather and 50% of the lambskin leather is waste (i.e., it is discarded during the production process and sold for other byproducts). After production, a goatskin jacket weighs approximately 3 pounds, and a lambskin jacket weighs approximately 2.5 pounds (neither with linings, which are added in the United States).
In the production of jackets at the plants, 37.5% of the goatskin leather and 50% of the lambskin leather is waste (i.e., it is discarded during the production process and sold for other byproducts). After production, a goatskin jacket weighs approximately 3 pounds, and a lambskin jacket weighs approximately 2.5 pounds (neither with linings, which are added in the United States).Following are the costs per pound, in U.S. dollars, for tanning the uncut leather, shipping it, and producing the leather jackets at each plant:
 Note that the cost of jacket production is the same for goatskin and lambskin. Also, leather can be tanned in France, Spain, and Italy and shipped directly to the South American plants for jacket production, but the opposite is not possible due to high tariff restrictions (i.e., tanned leather is not shipped to Europe for production).
Note that the cost of jacket production is the same for goatskin and lambskin. Also, leather can be tanned in France, Spain, and Italy and shipped directly to the South American plants for jacket production, but the opposite is not possible due to high tariff restrictions (i.e., tanned leather is not shipped to Europe for production).Once the leather jackets are produced at the plants in Europe and South America, Erken transports them to ports in Lisbon, Marseilles, and Caracas and then from these ports to U.S. ports in New Orleans, Jacksonville, and Savannah. The available shipping capacity at each port and the transportation costs from the plants to the ports are as follows:
 The shipping costs ($/lb.) from each port in Europe and South America to the U.S. ports and the available truck and rail capacity for transport at the U.S. ports are as follows:
The shipping costs ($/lb.) from each port in Europe and South America to the U.S. ports and the available truck and rail capacity for transport at the U.S. ports are as follows: The transportation costs ($/lb.) from the U.S. ports to the three distribution centers are as follows:
The transportation costs ($/lb.) from the U.S. ports to the three distribution centers are as follows: Erken wants to determine the least costly shipments of material and jackets that will meet the demand at the U.S. distribution centers. Develop a transshipment model for Erken that will result in a minimum cost solution.
Erken wants to determine the least costly shipments of material and jackets that will meet the demand at the U.S. distribution centers. Develop a transshipment model for Erken that will result in a minimum cost solution.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
77
The Interstate Truck Rental firm has accumulated extra trucks at three of its truck leasing outlets, as shown in the following table:
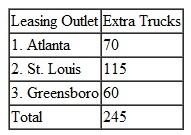 The firm also has four outlets with shortages of rental trucks, as follows:
The firm also has four outlets with shortages of rental trucks, as follows:
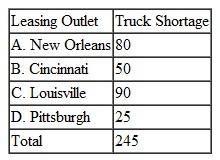 The firm wants to transfer trucks from those outlets with extras to those with shortages at the minimum total cost. The following costs of transporting these trucks from city to city have been determined:
The firm wants to transfer trucks from those outlets with extras to those with shortages at the minimum total cost. The following costs of transporting these trucks from city to city have been determined:
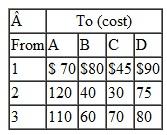 Solve this problem by using the computer.
Solve this problem by using the computer.
 The firm also has four outlets with shortages of rental trucks, as follows:
The firm also has four outlets with shortages of rental trucks, as follows: The firm wants to transfer trucks from those outlets with extras to those with shortages at the minimum total cost. The following costs of transporting these trucks from city to city have been determined:
The firm wants to transfer trucks from those outlets with extras to those with shortages at the minimum total cost. The following costs of transporting these trucks from city to city have been determined: Solve this problem by using the computer.
Solve this problem by using the computer.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
78
Suntrek, based in China, is a global supplier of denim jeans for apparel companies around the world. They purchase raw cotton from producers in Arkansas, Mississippi, and Texas, where it is picked, ginned, and baled and then transported by flatbed trucks to ports in Houston, New Orleans, Savannah, and Charleston, where it is loaded into 80-foot containers and shipped to factories overseas. For the coming year Suntrek has contracted with its U.S. broker for 71,000 (550 lb.) bales of cotton and the transportation and handling costs from each cotton-processing facility to each port, and the container capacity (in bales) at each port are as follows:
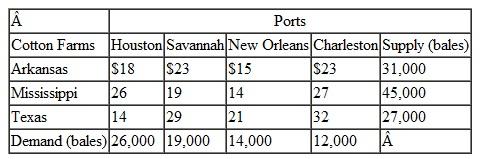 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
 Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Determine the optimal shipments from each processing facility to each port that will result in the minimum shipping cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
79
Horizon Computers manufactures laptops in Germany, Belgium, and Italy. Because of high tariffs between international trade groups, it is sometimes cheaper to ship partially completed laptops to factories in Puerto Rico, Mexico, and Panama and have them completed before final shipment to U.S. distributors in Texas, Virginia, and Ohio. The cost ($/unit) of the completed laptops plus tariffs and shipment costs from the European plants directly to the United States and supply and demand are as follows:
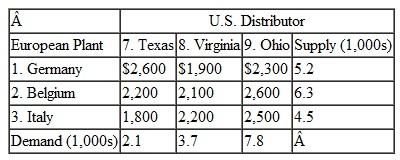 Alternatively, the unit costs of shipping partially completed laptops to plants for finishing before sending them to the United States are as follows:
Alternatively, the unit costs of shipping partially completed laptops to plants for finishing before sending them to the United States are as follows:
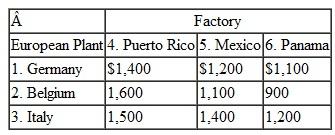
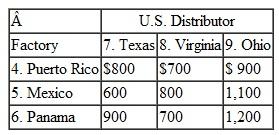 Determine the optimal shipments of laptops that will meet demand at the U.S. distributors at the minimum total cost.
Determine the optimal shipments of laptops that will meet demand at the U.S. distributors at the minimum total cost.
 Alternatively, the unit costs of shipping partially completed laptops to plants for finishing before sending them to the United States are as follows:
Alternatively, the unit costs of shipping partially completed laptops to plants for finishing before sending them to the United States are as follows:
 Determine the optimal shipments of laptops that will meet demand at the U.S. distributors at the minimum total cost.
Determine the optimal shipments of laptops that will meet demand at the U.S. distributors at the minimum total cost.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
80
In Problem, officials 2 and 8 recently had a confrontation with one of the coaches in the game in Athens. They were forced to eject the coach after several technical fouls. The conference office decided that it would not be a good idea to have these two officials work the Athens game so soon after this confrontation, so they decided that officials 2 and 8 will not be assigned to the Athens game. How will this affect the optimal solution to this problem
Problem
The Southeastern Conference has nine basketball officials who must be assigned to three conference games, three to each game. The conference office wants to assign the officials so that the total distance they travel will be minimized. The distance (in miles) each official would travel to each game is given in the following table:
 Determine the optimal assignment(s) to minimize the total distance traveled by the officials.
Determine the optimal assignment(s) to minimize the total distance traveled by the officials.
Problem
The Southeastern Conference has nine basketball officials who must be assigned to three conference games, three to each game. The conference office wants to assign the officials so that the total distance they travel will be minimized. The distance (in miles) each official would travel to each game is given in the following table:
 Determine the optimal assignment(s) to minimize the total distance traveled by the officials.
Determine the optimal assignment(s) to minimize the total distance traveled by the officials.
Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck


