Deck 15: Labor Markets
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/11
Play
Full screen (f)
Deck 15: Labor Markets
1
Suppose there are 8,000 hours in a year (actually there are 8,760) and that an individual has a potential market wage of $5 per hour.
a. What is the individual's full income? If he or she chooses to devote 75 percent of this income to leisure, how many hours will be worked?
b. Suppose a rich uncle dies and leaves the individual an annual income of $4,000 per year. If he or she continues to devote 75 percent of full income to leisure, how many hours will be worked?
c. How would your answer to part (b) change if the market wage were $10 per hour instead of $5 per hour?
d. Graph the individual's supply of labor curve implied by parts (b) and (c).
a. What is the individual's full income? If he or she chooses to devote 75 percent of this income to leisure, how many hours will be worked?
b. Suppose a rich uncle dies and leaves the individual an annual income of $4,000 per year. If he or she continues to devote 75 percent of full income to leisure, how many hours will be worked?
c. How would your answer to part (b) change if the market wage were $10 per hour instead of $5 per hour?
d. Graph the individual's supply of labor curve implied by parts (b) and (c).




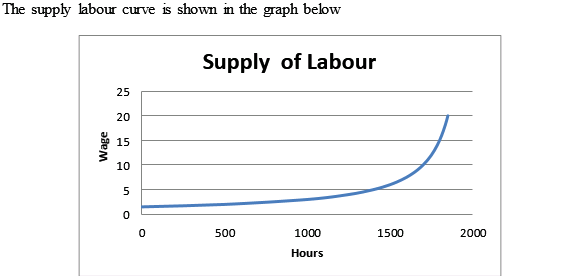
2
As we saw in this chapter, the elements of labor supply theory can also be derived from an expenditure-minimization approach. Suppose a person's utility function for consumption and leisure takes the Cobb-Douglas form
 . Then the expenditure-minimization problem is
. Then the expenditure-minimization problem is
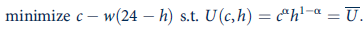
a. Use this approach to derive the expenditure function for this problem.
b. Use the envelope theorem to derive the compensated demand functions for consumption and leisure.
c. Derive the compensated labor supply function. Show that
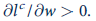 .
.
d. Compare the compensated labor supply function from part (c) to the uncompensated labor supply function in Example 16.2 (with n =0). Use the Slutsky equation to show why income and substitution effects of a change in the real wage are precisely offsetting in the uncompensated Cobb-Douglas labor supply function
 . Then the expenditure-minimization problem is
. Then the expenditure-minimization problem is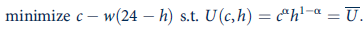
a. Use this approach to derive the expenditure function for this problem.
b. Use the envelope theorem to derive the compensated demand functions for consumption and leisure.
c. Derive the compensated labor supply function. Show that
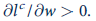 .
.d. Compare the compensated labor supply function from part (c) to the uncompensated labor supply function in Example 16.2 (with n =0). Use the Slutsky equation to show why income and substitution effects of a change in the real wage are precisely offsetting in the uncompensated Cobb-Douglas labor supply function
In order to find the optimal consumption bundle an individual either can maximize his utility with given income or can minimize the expenditure to attain a particular level of utility.
The utility function for an individual in terms of consumption and leisure is given below:
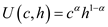 The expenditure need to be minimized given the utility level at
The expenditure need to be minimized given the utility level at
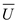 .
.
a.
Setting the Lagrange equation to minimize the expenditure given utility level at
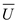 as shown below:
as shown below:
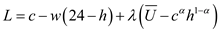 The first order conditions of Lagrange equation can be computed as shown below:
The first order conditions of Lagrange equation can be computed as shown below:
 Set first order conditions equal to zero and solve it to get the value of optimal consumption bundle as shown below:
Set first order conditions equal to zero and solve it to get the value of optimal consumption bundle as shown below:


 Solving the first order differentials the value of c and h can be computed as shown below:
Solving the first order differentials the value of c and h can be computed as shown below:




 The expenditure function can be shown as given below:
The expenditure function can be shown as given below:
 b.
b.
The compensated demand function is the demand function for any commodity keeping the utility level at a particular constant level.
The compensated demand function for leisure can be computed by using envelope theorem as shown below:

 The compensated demand function for consumption can't be computed as price of consumption here is treated as numeriare.
The compensated demand function for consumption can't be computed as price of consumption here is treated as numeriare.
c.
The compensated labor supply function can be calculated as shown below:
 The derivative of compensated labor supply function with respect to w is shown below:
The derivative of compensated labor supply function with respect to w is shown below:
 As
As
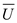 and w is positive integer the value of compensated supply function will rise with rise in w that is the curve will be positively sloped.
and w is positive integer the value of compensated supply function will rise with rise in w that is the curve will be positively sloped.
d.
The compensated labor supply curve is given below:
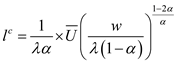 The uncompensated labor supply is given below:
The uncompensated labor supply is given below:
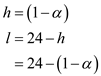 The uncompensated demand curve is function of only
The uncompensated demand curve is function of only
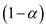 that is the share of utility of leisure. Whereas the compensated demand curve is the function of constant utility and wage rate too.
that is the share of utility of leisure. Whereas the compensated demand curve is the function of constant utility and wage rate too.
The Slutsky equation breaks the change in demand for one good in response to a change in the price of other good.
The slustky equation is given below:
 In this case the income and substitution effect of real wages on uncompensated labor supply curve is offset by each other.
In this case the income and substitution effect of real wages on uncompensated labor supply curve is offset by each other.

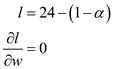 Income effect of wage rise is zero.
Income effect of wage rise is zero.
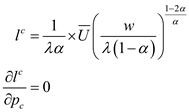 Substitution effect is also zero.
Substitution effect is also zero.
So, rise in wages will not affect the uncompensated supply of labor.
The utility function for an individual in terms of consumption and leisure is given below:
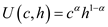 The expenditure need to be minimized given the utility level at
The expenditure need to be minimized given the utility level at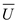 .
. a.
Setting the Lagrange equation to minimize the expenditure given utility level at
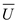 as shown below:
as shown below: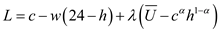 The first order conditions of Lagrange equation can be computed as shown below:
The first order conditions of Lagrange equation can be computed as shown below: Set first order conditions equal to zero and solve it to get the value of optimal consumption bundle as shown below:
Set first order conditions equal to zero and solve it to get the value of optimal consumption bundle as shown below:

 Solving the first order differentials the value of c and h can be computed as shown below:
Solving the first order differentials the value of c and h can be computed as shown below:



 The expenditure function can be shown as given below:
The expenditure function can be shown as given below: b.
b.The compensated demand function is the demand function for any commodity keeping the utility level at a particular constant level.
The compensated demand function for leisure can be computed by using envelope theorem as shown below:

 The compensated demand function for consumption can't be computed as price of consumption here is treated as numeriare.
The compensated demand function for consumption can't be computed as price of consumption here is treated as numeriare.c.
The compensated labor supply function can be calculated as shown below:
 The derivative of compensated labor supply function with respect to w is shown below:
The derivative of compensated labor supply function with respect to w is shown below: As
As 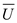 and w is positive integer the value of compensated supply function will rise with rise in w that is the curve will be positively sloped.
and w is positive integer the value of compensated supply function will rise with rise in w that is the curve will be positively sloped.d.
The compensated labor supply curve is given below:
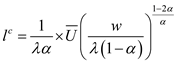 The uncompensated labor supply is given below:
The uncompensated labor supply is given below: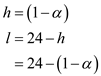 The uncompensated demand curve is function of only
The uncompensated demand curve is function of only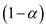 that is the share of utility of leisure. Whereas the compensated demand curve is the function of constant utility and wage rate too.
that is the share of utility of leisure. Whereas the compensated demand curve is the function of constant utility and wage rate too.The Slutsky equation breaks the change in demand for one good in response to a change in the price of other good.
The slustky equation is given below:
 In this case the income and substitution effect of real wages on uncompensated labor supply curve is offset by each other.
In this case the income and substitution effect of real wages on uncompensated labor supply curve is offset by each other.
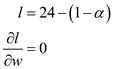 Income effect of wage rise is zero.
Income effect of wage rise is zero.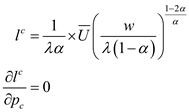 Substitution effect is also zero.
Substitution effect is also zero.So, rise in wages will not affect the uncompensated supply of labor.
3
A welfare program for low-income people offers a family a basic grant of $6,000 per year. This grant is reduced by $0.75 for each $1 of other income the family has.
a. How much in welfare benefits does the family receive if it has no other income? If the head of the family earns $2,000 per year? How about $4,000 per year?
b. At what level of earnings does the welfare grant become zero?
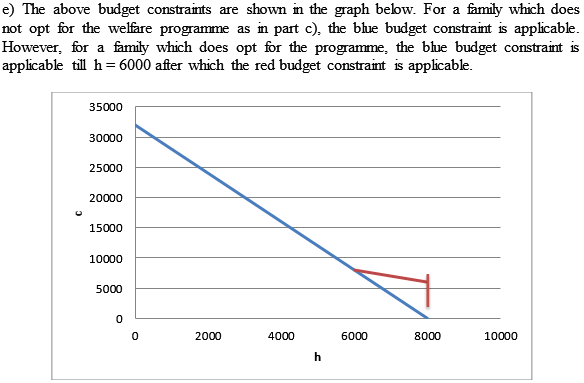
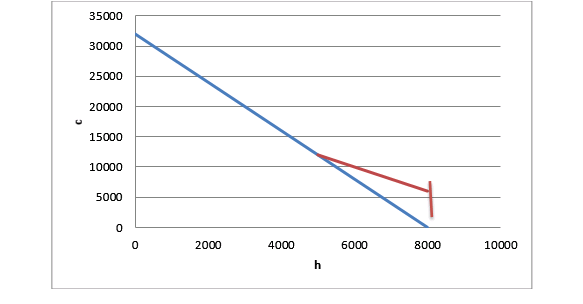
c. Assume the head of this family can earn $4 per hour and that the family has no other income. What is the annual budget constraint for this family if it does not participate in the welfare program? That is, how are consumption (c) and hours of leisure (h) related?
d. What is the budget constraint if the family opts to participate in the welfare program? (Remember, the welfare grant can only be positive.)
e. Graph your results from parts (c) and (d).
f. Suppose the government changes the rules of the welfare program to permit families to keep 50 percent of what they earn. How would this change your answers to parts (d) and (e)?
g. Using your results from part (f), can you predict whether the head of this family will work more or less under the new rules described in part (f )?
a. How much in welfare benefits does the family receive if it has no other income? If the head of the family earns $2,000 per year? How about $4,000 per year?
b. At what level of earnings does the welfare grant become zero?
c. Assume the head of this family can earn $4 per hour and that the family has no other income. What is the annual budget constraint for this family if it does not participate in the welfare program? That is, how are consumption (c) and hours of leisure (h) related?
d. What is the budget constraint if the family opts to participate in the welfare program? (Remember, the welfare grant can only be positive.)
e. Graph your results from parts (c) and (d).
f. Suppose the government changes the rules of the welfare program to permit families to keep 50 percent of what they earn. How would this change your answers to parts (d) and (e)?
g. Using your results from part (f), can you predict whether the head of this family will work more or less under the new rules described in part (f )?
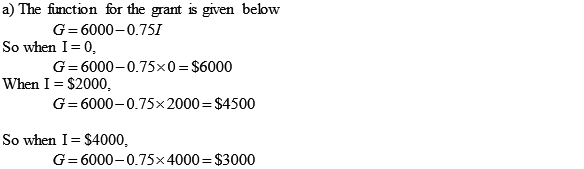

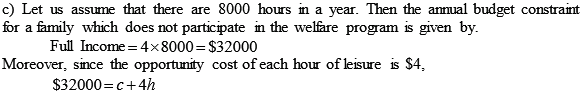


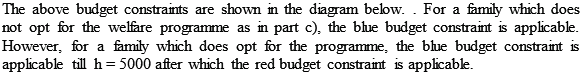
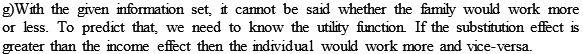
4
Suppose demand for labor is given by
l = _50w + 450
and supply is given by
l = 100w,
where l represents the number of people employed and w is the real wage rate per hour.
a. What will be the equilibrium levels for w and l in this market?
b. Suppose the government wishes to increase the equilibrium wage to $4 per hour by offering a subsidy to employers for each person hired. How much will this subsidy have to be? What will the new equilibrium level of employment be? How much total subsidy will be paid?
c. Suppose instead that the government declared a minimum wage of $4 per hour. How much labor would be demanded at this price? How much unemployment would there be?
d. Graph your results.
l = _50w + 450
and supply is given by
l = 100w,
where l represents the number of people employed and w is the real wage rate per hour.
a. What will be the equilibrium levels for w and l in this market?
b. Suppose the government wishes to increase the equilibrium wage to $4 per hour by offering a subsidy to employers for each person hired. How much will this subsidy have to be? What will the new equilibrium level of employment be? How much total subsidy will be paid?
c. Suppose instead that the government declared a minimum wage of $4 per hour. How much labor would be demanded at this price? How much unemployment would there be?
d. Graph your results.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
5
Carl the clothier owns a large garment factory on an isolated island. Carl's factory is the only source of employment for most of the islanders, and thus Carl acts as a monopsonist. The supply curve for garment workers is given by
l = 80w,
where l is the number of workers hired and w is their hourly wage. Assume also that Carl's labor demand (marginal revenue product) curve is given by
l = 400 - 40MRPl :
a. How many workers will Carl hire to maximize his profits, and what wage will he pay?
b. Assume now that the government implements a minimum wage law covering all garment workers. How many workers will Carl now hire, and how much unemployment will there be if the minimum wage is set at $4 per hour?
c. Graph your results.
d. How does a minimum wage imposed under monopsony differ in results as compared with a minimum wage imposed under perfect competition? (Assume the minimum wage is above the market-determined wage.)
l = 80w,
where l is the number of workers hired and w is their hourly wage. Assume also that Carl's labor demand (marginal revenue product) curve is given by
l = 400 - 40MRPl :
a. How many workers will Carl hire to maximize his profits, and what wage will he pay?
b. Assume now that the government implements a minimum wage law covering all garment workers. How many workers will Carl now hire, and how much unemployment will there be if the minimum wage is set at $4 per hour?
c. Graph your results.
d. How does a minimum wage imposed under monopsony differ in results as compared with a minimum wage imposed under perfect competition? (Assume the minimum wage is above the market-determined wage.)

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
6
The Ajax Coal Company is the only hirer of labor in its area. It can hire any number of female workers or male workers it wishes. The supply curve for women is given by
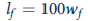
and for men by
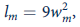 ,
,
where w f and w m are the hourly wage rates paid to female and male workers, respectively. Assume that Ajax sells its coal in a perfectly competitive market at $5 per ton and that each worker hired (both men and women) can mine 2 tons per hour. If the firm wishes to maximize profits, how many female and male workers should be hired, and what will the wage rates be for these two groups? How much will Ajax earn in profits per hour on its mine machinery? How will that result compare to one in which Ajax was constrained (say, by market forces) to pay all workers the same wage based on the value of their marginal products?
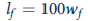
and for men by
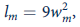 ,
,where w f and w m are the hourly wage rates paid to female and male workers, respectively. Assume that Ajax sells its coal in a perfectly competitive market at $5 per ton and that each worker hired (both men and women) can mine 2 tons per hour. If the firm wishes to maximize profits, how many female and male workers should be hired, and what will the wage rates be for these two groups? How much will Ajax earn in profits per hour on its mine machinery? How will that result compare to one in which Ajax was constrained (say, by market forces) to pay all workers the same wage based on the value of their marginal products?

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
7
Universal Fur is located in Clyde, Baffin Island, and sells high-quality fur bow ties throughout the world at a price of $5 each. The production function for fur bow ties (q) is given by
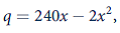
where x is the quantity of pelts used each week. Pelts are supplied only by Dan's Trading Post, which obtains them by hiring
Eskimo trappers at a rate of $10 per day. Dan's weekly production function for pelts is given by
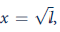 ,
,
where l represents the number of days of Eskimo time used each week.
a. For a quasi-competitive case in which both Universal Fur and Dan's Trading Post act as price-takers for pelts, what will be the equilibrium price (px) and how many pelts will be traded?
b. Suppose Dan acts as a monopolist, while Universal Fur continues to be a price-taker. What equilibrium will emerge in the pelt market?
c. Suppose Universal Fur acts as a monopsonist but Dan acts as a price-taker. What will the equilibrium be?
d. Graph your results, and discuss the type of equilibrium that is likely to emerge in the bilateral monopoly bargaining between Universal Fur and Dan.
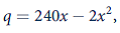
where x is the quantity of pelts used each week. Pelts are supplied only by Dan's Trading Post, which obtains them by hiring
Eskimo trappers at a rate of $10 per day. Dan's weekly production function for pelts is given by
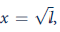 ,
,where l represents the number of days of Eskimo time used each week.
a. For a quasi-competitive case in which both Universal Fur and Dan's Trading Post act as price-takers for pelts, what will be the equilibrium price (px) and how many pelts will be traded?
b. Suppose Dan acts as a monopolist, while Universal Fur continues to be a price-taker. What equilibrium will emerge in the pelt market?
c. Suppose Universal Fur acts as a monopsonist but Dan acts as a price-taker. What will the equilibrium be?
d. Graph your results, and discuss the type of equilibrium that is likely to emerge in the bilateral monopoly bargaining between Universal Fur and Dan.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
8
Following in the spirit of the labor market game described in Example 16.6, suppose the firm's total revenue function is given by
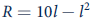
and the union's utility is simply a function of the total wage bill:
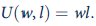
a. What is the Nash equilibrium wage contract in the two-stage game described in Example 16.6?
b. Show that the alternative wage contract w' = l ' = 4 is Pareto superior to the contract identified in part (a).
c. Under what conditions would the contract described in part (b) be sustainable as a subgame-perfect equilibrium?
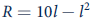
and the union's utility is simply a function of the total wage bill:
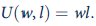
a. What is the Nash equilibrium wage contract in the two-stage game described in Example 16.6?
b. Show that the alternative wage contract w' = l ' = 4 is Pareto superior to the contract identified in part (a).
c. Under what conditions would the contract described in part (b) be sustainable as a subgame-perfect equilibrium?

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
9
Compensating wage differentials for risk
An individual receives utility from daily income (y), given by
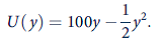
The only source of income is earnings. Hence y = wl , where w is the hourly wage and l is hours worked per day. The individual knows of a job that pays $5 per hour for a certain 8-hour day. What wage must be offered for a construction job where hours of work are random-with a mean of 8 hours and a standard deviation of 6 hours-to get the individual to accept this more ''risky'' job? Hint: This problem makes use of the statistical identity
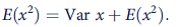
An individual receives utility from daily income (y), given by
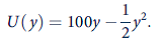
The only source of income is earnings. Hence y = wl , where w is the hourly wage and l is hours worked per day. The individual knows of a job that pays $5 per hour for a certain 8-hour day. What wage must be offered for a construction job where hours of work are random-with a mean of 8 hours and a standard deviation of 6 hours-to get the individual to accept this more ''risky'' job? Hint: This problem makes use of the statistical identity
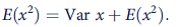

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
10
Family labor supply
A family with two adult members seeks to maximize a utility function of the form
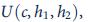
where c is family consumption and h 1 and h 2 are hours of leisure of each family member. Choices are constrained by
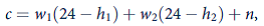
where w 1 and w 2 are the wages of each family member and n is nonlabor income.
a. Without attempting a mathematical presentation, use the notions of substitution and income effects to discuss the likely signs of the cross-substitution effects
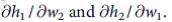 .
.
b. Suppose that one family member (say, individual 1) can work in the home, thereby converting leisure hours into consumption according to the function
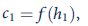
where
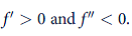 . How might this additional option affect the optimal division of work among family members?
. How might this additional option affect the optimal division of work among family members?
A family with two adult members seeks to maximize a utility function of the form
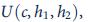
where c is family consumption and h 1 and h 2 are hours of leisure of each family member. Choices are constrained by
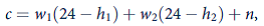
where w 1 and w 2 are the wages of each family member and n is nonlabor income.
a. Without attempting a mathematical presentation, use the notions of substitution and income effects to discuss the likely signs of the cross-substitution effects
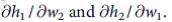 .
.b. Suppose that one family member (say, individual 1) can work in the home, thereby converting leisure hours into consumption according to the function
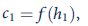
where
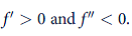 . How might this additional option affect the optimal division of work among family members?
. How might this additional option affect the optimal division of work among family members?
Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
11
A few results from demand theory
The theory developed in this chapter treats labor supply as the mirror image of the demand for leisure. Hence, the entire body of demand theory developed in Part 2 of the text becomes relevant to the study of labor supply as well. Here are three examples.
a. Roy's identity. In the Extensions to Chapter 5 we showed how demand functions can be derived from indirect utility functions by using Roy's identity. Use a similar approach to show that the labor supply function associated with the utility maximization problem described in Equation 16.20 can be derived from the indirect utility function by
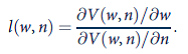
Illustrate this result for the Cobb-Douglas case described in Example 16.1.
b. Substitutes and complements. A change in the real wage will affect not only labor supply, but also the demand for specific items in the preferred consumption bundle. Develop a Slutsky-type equation for the cross-price effect of a change in w on a particular consumption item and then use it to discuss whether leisure and the item are (net or gross) substitutes or complements. Provide an example of each type of relationship.
c. Labor supply and marginal expense. Use a derivation similar to that used to calculate marginal revenue for a given
demand curve to show that
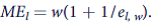
The theory developed in this chapter treats labor supply as the mirror image of the demand for leisure. Hence, the entire body of demand theory developed in Part 2 of the text becomes relevant to the study of labor supply as well. Here are three examples.
a. Roy's identity. In the Extensions to Chapter 5 we showed how demand functions can be derived from indirect utility functions by using Roy's identity. Use a similar approach to show that the labor supply function associated with the utility maximization problem described in Equation 16.20 can be derived from the indirect utility function by
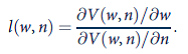
Illustrate this result for the Cobb-Douglas case described in Example 16.1.
b. Substitutes and complements. A change in the real wage will affect not only labor supply, but also the demand for specific items in the preferred consumption bundle. Develop a Slutsky-type equation for the cross-price effect of a change in w on a particular consumption item and then use it to discuss whether leisure and the item are (net or gross) substitutes or complements. Provide an example of each type of relationship.
c. Labor supply and marginal expense. Use a derivation similar to that used to calculate marginal revenue for a given
demand curve to show that
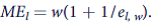

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck


