Deck 6: The Trigonometric Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/150
Play
Full screen (f)
Deck 6: The Trigonometric Functions
1
Simplify the expression. 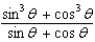
A)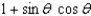
B)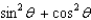
C)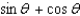
D)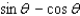
E)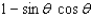
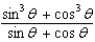
A)
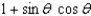
B)
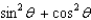
C)
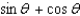
D)
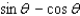
E)
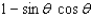
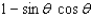
2
Approximate, to the nearest 0.01 radian, all angles  in the interval [ 0, 2
in the interval [ 0, 2 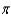 ) that satisfy the equation.
) that satisfy the equation. 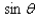 = 0.8412
= 0.8412
A)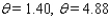
B)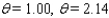
C)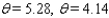
D)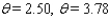
E)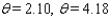
 in the interval [ 0, 2
in the interval [ 0, 2 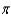 ) that satisfy the equation.
) that satisfy the equation. 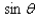 = 0.8412
= 0.8412A)
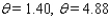
B)
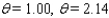
C)
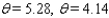
D)
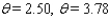
E)
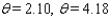
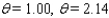
3
Verify the identity by transforming the left-hand side into the right-hand side. 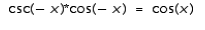
A)False
B)True
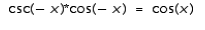
A)False
B)True
False
4
Express  = 2 in terms of degrees, minutes, and seconds, to the nearest second.
= 2 in terms of degrees, minutes, and seconds, to the nearest second.
A)
B)
C)
D)
E)
 = 2 in terms of degrees, minutes, and seconds, to the nearest second.
= 2 in terms of degrees, minutes, and seconds, to the nearest second.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
5
Find the quadrant containing  if the given conditions are true.
if the given conditions are true. 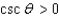 and
and 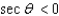
A)IV
B)II
C)I
D)III
 if the given conditions are true.
if the given conditions are true. 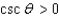 and
and 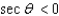
A)IV
B)II
C)I
D)III

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
6
Let P ( t ) be the point on the unit circle U that corresponds to t. If P ( t ) has the coordinates 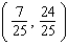 , find
, find 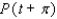 ,
, 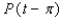 ,
, 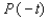 ,
, 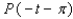 .
.
A)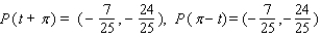
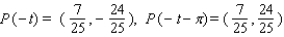
B)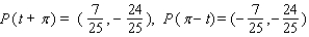
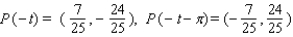
C)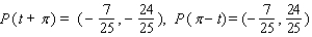
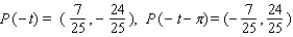
D)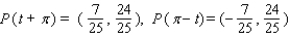
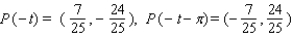
E)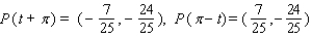
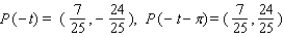
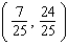 , find
, find 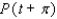 ,
, 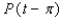 ,
, 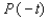 ,
, 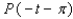 .
.A)
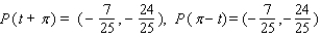
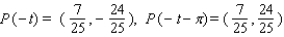
B)
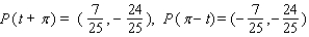
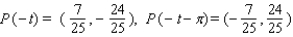
C)
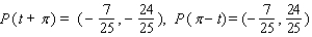
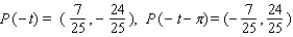
D)
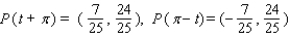
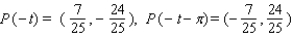
E)
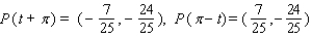
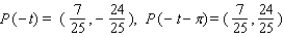

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
7
If a circular arc of the length s = 11 cm subtends the central angle  = 2 on a circle, find the radius of the circle.
= 2 on a circle, find the radius of the circle.
A)6.5 cm
B)5.5 cm
C)7 cm
D)22 cm
E)6 cm
 = 2 on a circle, find the radius of the circle.
= 2 on a circle, find the radius of the circle.A)6.5 cm
B)5.5 cm
C)7 cm
D)22 cm
E)6 cm

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
8
Two stars that are very close may appear to be one. The ability of a telescope to separate their images is called its resolution. The smaller the resolution, the better a telescope's ability to separate images in the sky. In a refracting telescope, resolution  ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 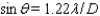 , where
, where 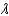 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 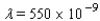 meter, its resolution is
meter, its resolution is 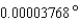 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)0.02 meters
B)1.17 meters
C)0.97 meters
D)0.77 meters
E)1.02 meters
 ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 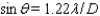 , where
, where 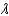 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 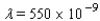 meter, its resolution is
meter, its resolution is 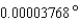 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)0.02 meters
B)1.17 meters
C)0.97 meters
D)0.77 meters
E)1.02 meters

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
9
Scientists sometimes use the formula 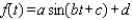 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in  , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 32
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 32  occurs at 2 P.M., and the average temperature of 23
occurs at 2 P.M., and the average temperature of 23  occurs 6 hours later.
occurs 6 hours later.
A)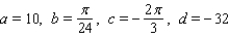
B)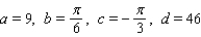
C)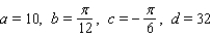
D)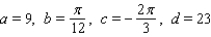
E)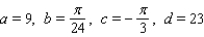
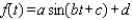 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in 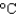 , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 32
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 32  occurs at 2 P.M., and the average temperature of 23
occurs at 2 P.M., and the average temperature of 23 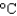 occurs 6 hours later.
occurs 6 hours later.A)
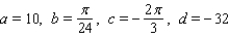
B)
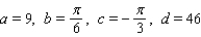
C)
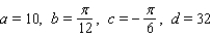
D)
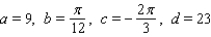
E)
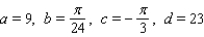

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
10
Find the period of the equation. 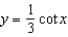
A)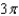
B)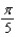
C)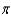
D)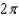
E)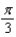
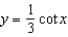
A)
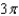
B)
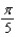
C)
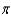
D)
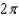
E)
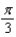

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
11
Find the amplitude, the period, and the phase shift. 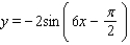
A)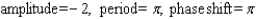
B)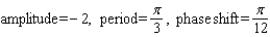
C)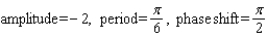
D)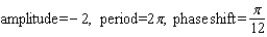
E)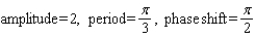
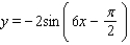
A)
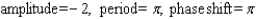
B)
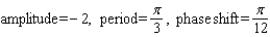
C)
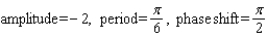
D)
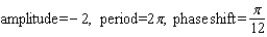
E)
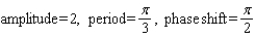

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
12
Express the angle as a decimal, to the nearest ten-thousandth of a degree. 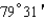
A)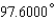
B)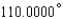
C)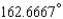
D)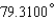
E)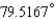
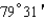
A)
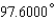
B)
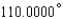
C)
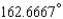
D)
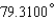
E)
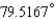

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
13
Points on the terminal sides of angles play an important part in the design of arms for robots. Suppose a robot has a straight arm 18 inches long that can rotate about the origin in a coordinate plane. If the robot's hand is located at (18, 0) and then rotates through an angle of 60 o , what is the new location of the hand?
A)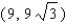
B)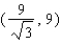
C)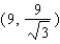
D)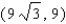
E)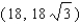
A)
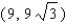
B)
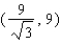
C)
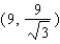
D)
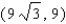
E)
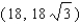

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
14
Approximate to four decimal places. 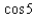
A)0.2683
B)0.2713
C)0.2837
D)0.5425
E)0.2327
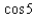
A)0.2683
B)0.2713
C)0.2837
D)0.5425
E)0.2327

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
15
Approximate the acute angle  to the nearest
to the nearest 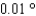 .
. 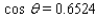
A)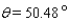
B)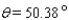
C)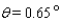
D)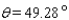
E)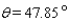
 to the nearest
to the nearest 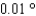 .
. 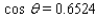
A)
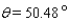
B)
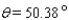
C)
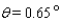
D)
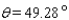
E)
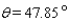

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
16
The popular biorhythm theory uses the graphs of three simple sine functions to make predictions about an individual's physical, emotional, and intellectual potential for a particular day. The graphs are given by 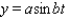 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 19 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 19 days.
A)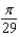
B)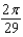
C)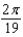
D)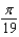
E)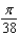
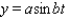 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 19 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 19 days.A)
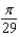
B)
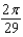
C)
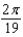
D)
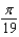
E)
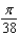

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
17
Refer to the graph of y = cos x to find the separate values of x in the interval 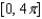 that satisfy the equation.
that satisfy the equation. 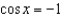
A)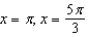
B)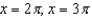
C)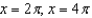
D)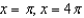
E)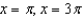
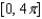 that satisfy the equation.
that satisfy the equation. 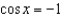
A)
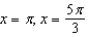
B)
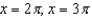
C)
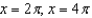
D)
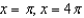
E)
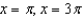

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
18
The amount of sunshine illuminating a wall of a building can greatly affect the energy efficiency of the building. The solar radiation striking a vertical wall that faces east is given by the formula 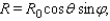 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 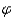 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with 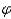 = 90 o when the sun is in the east and
= 90 o when the sun is in the east and 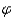 = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 30 o and the sun is in the southeast?
is equal to 30 o and the sun is in the southeast?
Round the answer to the nearest integer.
A)71 %
B)61 %
C)56 %
D)76 %
E)29 %
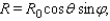 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 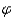 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with  = 90 o when the sun is in the east and
= 90 o when the sun is in the east and  = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 30 o and the sun is in the southeast?
is equal to 30 o and the sun is in the southeast?Round the answer to the nearest integer.
A)71 %
B)61 %
C)56 %
D)76 %
E)29 %

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
19
As 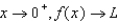 for some real number
for some real number 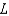 . Use a graph to predict
. Use a graph to predict 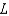 .
. 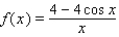
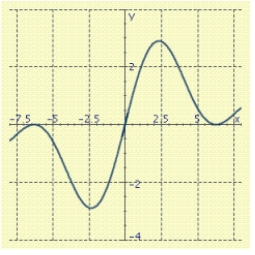
A)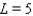
B)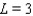
C)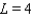
D)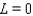
E)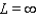
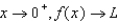 for some real number
for some real number 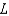 . Use a graph to predict
. Use a graph to predict 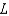 .
. 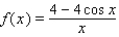

A)
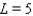
B)
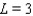
C)
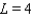
D)
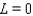
E)
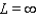

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
20
On a certain spring day with 12 hours of daylight, the light intensity I takes on its largest value of 390 calories/cm 2 at midday. If t = 0 corresponds to sunrise and t is measured in hours, find a formula I = a sin bt that fits this information.
A)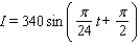
B)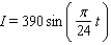
C)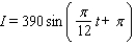
D)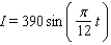
E)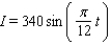
A)
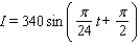
B)
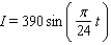
C)
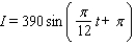
D)
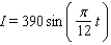
E)
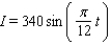

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
21
Simplify the expression. 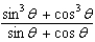
A)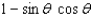
B)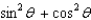
C)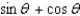
D)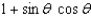
E)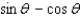
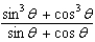
A)
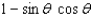
B)
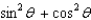
C)
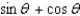
D)
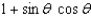
E)
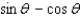

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
22
Approximate to four decimal places. 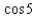
A)0.2837
B)0.2713
C)0.2683
D)0.2327
E)0.5425
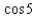
A)0.2837
B)0.2713
C)0.2683
D)0.2327
E)0.5425

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
23
Express  = 4.5 in terms of degrees, minutes, and seconds, to the nearest second.
= 4.5 in terms of degrees, minutes, and seconds, to the nearest second.
A)
B)
C)
D)
E)
 = 4.5 in terms of degrees, minutes, and seconds, to the nearest second.
= 4.5 in terms of degrees, minutes, and seconds, to the nearest second.A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
24
Approximate the acute angle  to the nearest
to the nearest 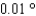 .
. 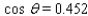
A)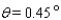
B)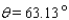
C)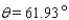
D)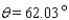
E)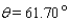
 to the nearest
to the nearest 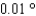 .
. 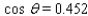
A)
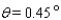
B)
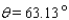
C)
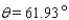
D)
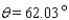
E)
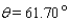

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
25
Let P ( t ) be the point on the unit circle U that corresponds to t. If P ( t ) has the coordinates 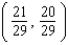 , find
, find 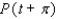 ,
, 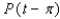 ,
, 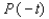 ,
, 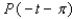 .
.
A)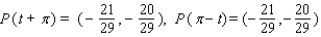
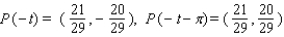
B)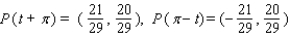
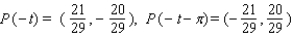
C)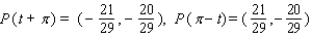
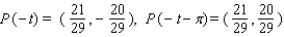
D)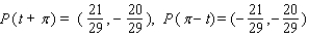
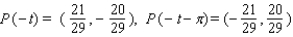
E)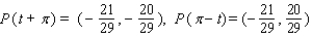
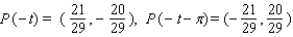
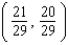 , find
, find 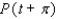 ,
, 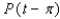 ,
, 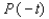 ,
, 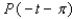 .
.A)
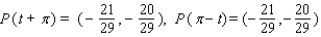
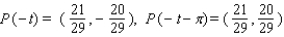
B)
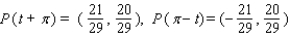
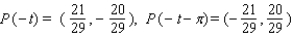
C)
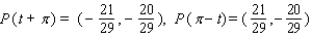
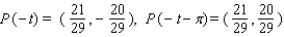
D)
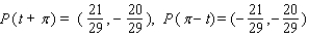
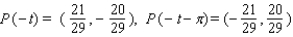
E)
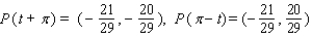
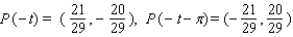

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
26
An airplane flying at a speed of 360 mi/hr flies from a point A in the direction 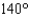 for 15 minutes and then flies in the direction
for 15 minutes and then flies in the direction 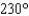 for 15 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 15 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
A)104 mi
B)127 mi
C)1 mi
D)254 mi
E)180 mi
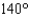 for 15 minutes and then flies in the direction
for 15 minutes and then flies in the direction 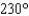 for 15 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 15 minutes. Approximate, to the nearest mile, the distance from the airplane to A.A)104 mi
B)127 mi
C)1 mi
D)254 mi
E)180 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
27
Points on the terminal sides of angles play an important part in the design of arms for robots. Suppose a robot has a straight arm 20 inches long that can rotate about the origin in a coordinate plane. If the robot's hand is located at (20, 0) and then rotates through an angle of 60 o , what is the new location of the hand?
A)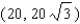
B)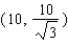
C)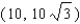
D)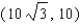
E)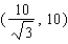
A)
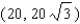
B)
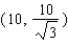
C)
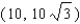
D)
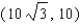
E)
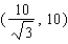

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
28
Verify the identity by transforming the left-hand side into the right-hand side. 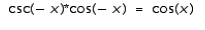
A)False
B)True
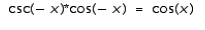
A)False
B)True

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
29
Radio stations often have more than one broadcasting tower because federal guidelines do not usually permit a radio station to broadcast its signal in all directions with equal power. Since radio waves can travel over long distances, it is important to control their directional patterns so that radio stations do not interfere with one another. Suppose that a radio station has two broadcasting towers located along a north-south line, as shown in the figure. If the radio station is broadcasting at a wavelength 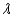 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 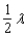 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 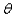 is given by
is given by 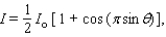 where I o is the maximum intensity.
where I o is the maximum intensity. 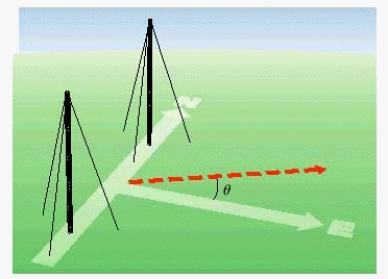 Approximate I in terms of I o for
Approximate I in terms of I o for 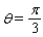 .
.
A)0.055I o
B)I o
C)0.033I o
D)0.066I o
E)0.044I o
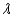 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 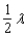 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 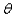 is given by
is given by 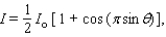 where I o is the maximum intensity.
where I o is the maximum intensity.  Approximate I in terms of I o for
Approximate I in terms of I o for 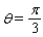 .
.A)0.055I o
B)I o
C)0.033I o
D)0.066I o
E)0.044I o

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
30
Refer to the graph of y = cos x to find the separate values of x in the interval 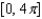 that satisfy the equation.
that satisfy the equation. 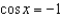
A)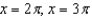
B)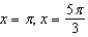
C)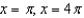
D)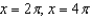
E)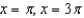
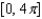 that satisfy the equation.
that satisfy the equation. 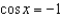
A)
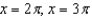
B)
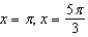
C)
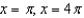
D)
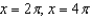
E)
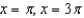

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
31
A ship leaves port at 4:00 P.M. and sails in the direction 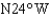 at a rate of 19 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction
at a rate of 19 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction 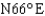 at a rate of 16 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
at a rate of 16 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
A)70 mi
B)17 mi
C)75 mi
D)25 mi
E)140 mi
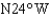 at a rate of 19 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction
at a rate of 19 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction 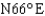 at a rate of 16 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
at a rate of 16 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?A)70 mi
B)17 mi
C)75 mi
D)25 mi
E)140 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
32
If a circular arc of the length s = 13.5 cm subtends the central angle  = 3 on a circle, find the radius of the circle.
= 3 on a circle, find the radius of the circle.
A)4.5 cm
B)5.5 cm
C)6 cm
D)40.5 cm
E)5 cm
 = 3 on a circle, find the radius of the circle.
= 3 on a circle, find the radius of the circle.A)4.5 cm
B)5.5 cm
C)6 cm
D)40.5 cm
E)5 cm

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
33
The amount of sunshine illuminating a wall of a building can greatly affect the energy efficiency of the building. The solar radiation striking a vertical wall that faces east is given by the formula 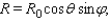 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 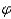 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with 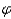 = 90 o when the sun is in the east and
= 90 o when the sun is in the east and 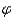 = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 60 o and the sun is in the southeast?
is equal to 60 o and the sun is in the southeast?
Round the answer to the nearest integer.
A)35 %
B)30 %
C)20 %
D)45 %
E)59 %
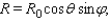 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 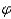 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with 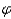 = 90 o when the sun is in the east and
= 90 o when the sun is in the east and 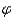 = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 60 o and the sun is in the southeast?
is equal to 60 o and the sun is in the southeast?Round the answer to the nearest integer.
A)35 %
B)30 %
C)20 %
D)45 %
E)59 %

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
34
Express the angle as a decimal, to the nearest ten-thousandth of a degree. 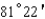
A)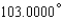
B)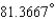
C)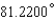
D)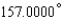
E)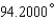
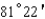
A)
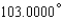
B)
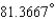
C)
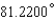
D)
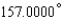
E)
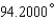

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
35
Two stars that are very close may appear to be one. The ability of a telescope to separate their images is called its resolution. The smaller the resolution, the better a telescope's ability to separate images in the sky. In a refracting telescope, resolution  ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 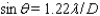 , where
, where 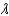 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 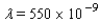 meter, its resolution is
meter, its resolution is 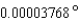 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)1.17 meters
B)0.77 meters
C)0.02 meters
D)0.97 meters
E)1.02 meters
 ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 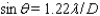 , where
, where 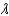 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 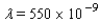 meter, its resolution is
meter, its resolution is 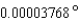 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)1.17 meters
B)0.77 meters
C)0.02 meters
D)0.97 meters
E)1.02 meters

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
36
Approximate, to the nearest 0.01 radian, all angles  in the interval [ 0, 2
in the interval [ 0, 2 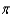 ) that satisfy the equation.
) that satisfy the equation. 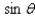 = 0.2518
= 0.2518
A)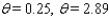
B)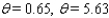
C)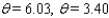
D)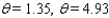
E)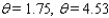
 in the interval [ 0, 2
in the interval [ 0, 2 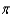 ) that satisfy the equation.
) that satisfy the equation. 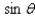 = 0.2518
= 0.2518A)
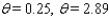
B)
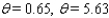
C)
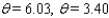
D)
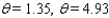
E)
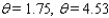

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
37
A CB antenna is located on the top of a garage that is 17 feet tall. From a point on level ground that is 120 feet from a point directly below the antenna, the antenna subtends an angle of 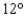 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 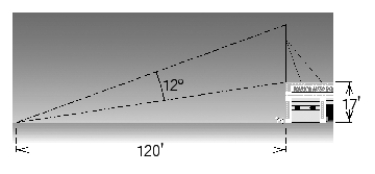
A)345.6 ft
B)26.8 ft
C)24.2 ft
D)36.8 ft
E)95.7 ft
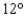 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 
A)345.6 ft
B)26.8 ft
C)24.2 ft
D)36.8 ft
E)95.7 ft

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
38
Find the quadrant containing  if the given conditions are true.
if the given conditions are true. 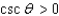 and
and 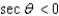
A)I
B)IV
C)II
D)III
 if the given conditions are true.
if the given conditions are true. 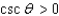 and
and 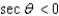
A)I
B)IV
C)II
D)III

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
39
Use the graph of a trigonometric function to aid in sketching the graph of the equation without plotting points. 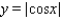
A)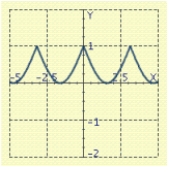
B)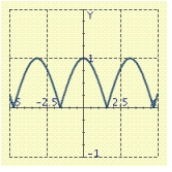
C)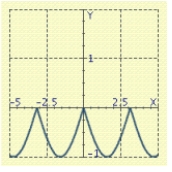
D)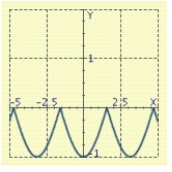
E)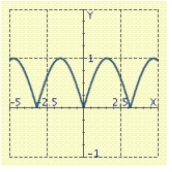
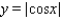
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
40
As 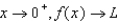 for some real number
for some real number 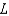 . Use a graph to predict
. Use a graph to predict 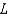 .
. 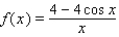
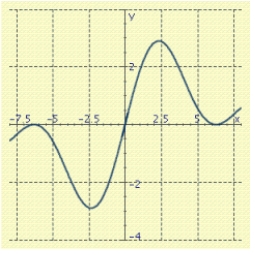
A)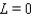
B)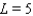
C)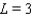
D)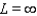
E)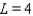
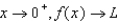 for some real number
for some real number 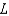 . Use a graph to predict
. Use a graph to predict 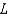 .
. 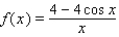

A)
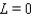
B)
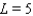
C)
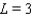
D)
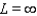
E)
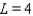

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
41
Let P ( t ) be the point on the unit circle U that corresponds to t. If P ( t ) has the coordinates 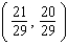 , find
, find 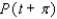 ,
, 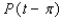 ,
, 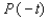 ,
, 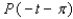 .
.
A)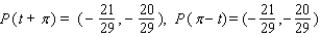
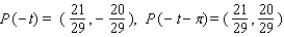
B)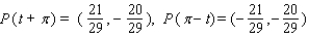
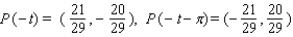
C)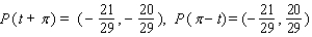
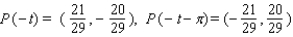
D)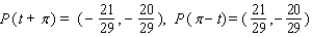
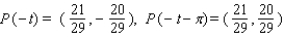
E)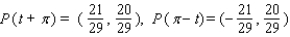
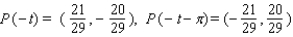
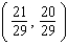 , find
, find 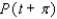 ,
, 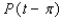 ,
, 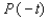 ,
, 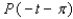 .
.A)
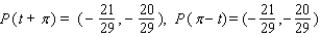
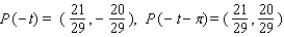
B)
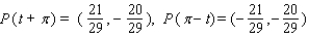
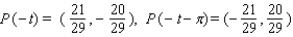
C)
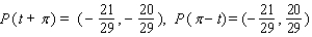
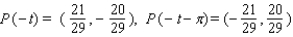
D)
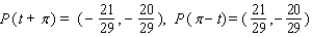
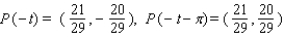
E)
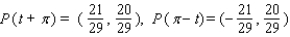
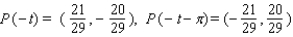

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
42
Two stars that are very close may appear to be one. The ability of a telescope to separate their images is called its resolution. The smaller the resolution, the better a telescope's ability to separate images in the sky. In a refracting telescope, resolution  ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 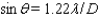 , where
, where 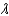 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 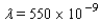 meter, its resolution is
meter, its resolution is 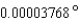 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)0.02 meters
B)0.77 meters
C)1.17 meters
D)0.97 meters
E)1.02 meters
 ( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between
( see the figure ) can be improved by using a lens with a larger diameter D. The relationship between  in degrees and D in meters is given by
in degrees and D in meters is given by 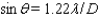 , where
, where 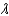 is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of
is the wavelength of light in meters. The largest refracting telescope in the world is at the University of Chicago. At a wavelength of 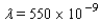 meter, its resolution is
meter, its resolution is 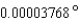 . Approximate the diameter of the lens to the nearest hundredth of a meter.
. Approximate the diameter of the lens to the nearest hundredth of a meter. 
A)0.02 meters
B)0.77 meters
C)1.17 meters
D)0.97 meters
E)1.02 meters

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
43
If a circular arc of the length s = 16 cm subtends the central angle  = 2 on a circle, find the radius of the circle.
= 2 on a circle, find the radius of the circle.
A)8.5 cm
B)32 cm
C)8 cm
D)9 cm
E)9.5 cm
 = 2 on a circle, find the radius of the circle.
= 2 on a circle, find the radius of the circle.A)8.5 cm
B)32 cm
C)8 cm
D)9 cm
E)9.5 cm

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
44
On a certain spring day with 12 hours of daylight, the light intensity I takes on its largest value of 480 calories/cm 2 at midday. If t = 0 corresponds to sunrise and t is measured in hours, find a formula I = a sin bt that fits this information.
A)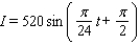
B)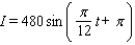
C)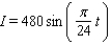
D)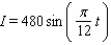
E)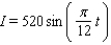
A)
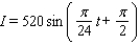
B)
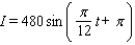
C)
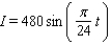
D)
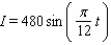
E)
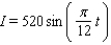

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
45
Scientists sometimes use the formula 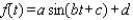 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in  , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 29
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 29  occurs at 2 P.M., and the average temperature of 21
occurs at 2 P.M., and the average temperature of 21  occurs 6 hours later.
occurs 6 hours later.
A)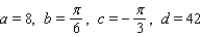
B)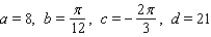
C)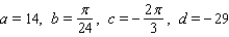
D)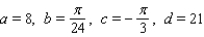
E)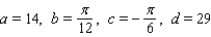
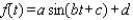 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in  , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 29
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 29  occurs at 2 P.M., and the average temperature of 21
occurs at 2 P.M., and the average temperature of 21  occurs 6 hours later.
occurs 6 hours later.A)
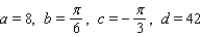
B)
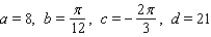
C)
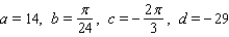
D)
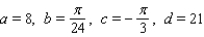
E)
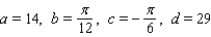

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
46
A ship leaves port at 4:00 P.M. and sails in the direction 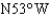 at a rate of 24 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction
at a rate of 24 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction 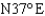 at a rate of 22 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
at a rate of 22 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
A)17 mi
B)182 mi
C)33 mi
D)98 mi
E)91 mi
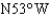 at a rate of 24 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction
at a rate of 24 mi/hr. Another ship leaves port at 4:30 P.M. and sails in the direction 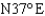 at a rate of 22 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?
at a rate of 22 mi/hr. Approximately how far apart are the ships at 7:00 P.M.?A)17 mi
B)182 mi
C)33 mi
D)98 mi
E)91 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
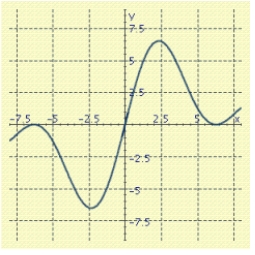
47
As 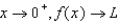 for some real number
for some real number  . Use a graph to predict
. Use a graph to predict  .
. 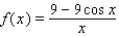
A)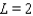
B)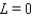
C)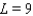
D)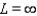
E)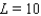
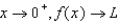 for some real number
for some real number 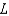 . Use a graph to predict
. Use a graph to predict 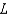 .
. 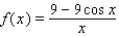

A)
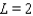
B)
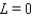
C)
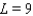
D)
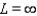
E)
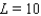

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
48
Find the period of the equation. 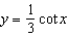
A)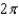
B)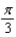
C)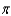
D)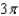
E)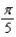
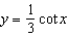
A)
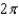
B)
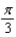
C)
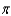
D)
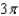
E)
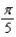

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
49
A CB antenna is located on the top of a garage that is 17 feet tall. From a point on level ground that is 120 feet from a point directly below the antenna, the antenna subtends an angle of 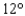 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 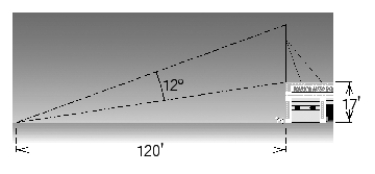
A)26.8 ft
B)345.6 ft
C)95.7 ft
D)36.8 ft
E)24.2 ft
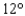 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 
A)26.8 ft
B)345.6 ft
C)95.7 ft
D)36.8 ft
E)24.2 ft

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
50
Express  = 2.5 in terms of degrees, minutes, and seconds, to the nearest second.
= 2.5 in terms of degrees, minutes, and seconds, to the nearest second.
A)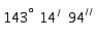
B)
C)
D)
E)
 = 2.5 in terms of degrees, minutes, and seconds, to the nearest second.
= 2.5 in terms of degrees, minutes, and seconds, to the nearest second.A)
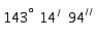
B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
51
Simplify the expression. 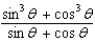
A)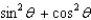
B)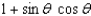
C)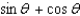
D)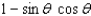
E)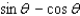
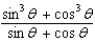
A)
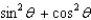
B)
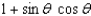
C)
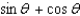
D)
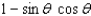
E)
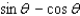

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
52
The popular biorhythm theory uses the graphs of three simple sine functions to make predictions about an individual's physical, emotional, and intellectual potential for a particular day. The graphs are given by 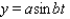 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 29 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 29 days.
A)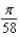
B)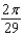
C)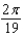
D)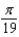
E)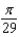
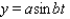 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 29 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 29 days.A)
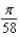
B)
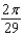
C)
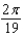
D)
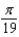
E)
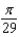

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
53
Radio stations often have more than one broadcasting tower because federal guidelines do not usually permit a radio station to broadcast its signal in all directions with equal power. Since radio waves can travel over long distances, it is important to control their directional patterns so that radio stations do not interfere with one another. Suppose that a radio station has two broadcasting towers located along a north-south line, as shown in the figure. If the radio station is broadcasting at a wavelength 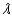 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 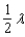 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 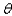 is given by
is given by 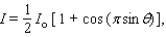 where I o is the maximum intensity.
where I o is the maximum intensity. 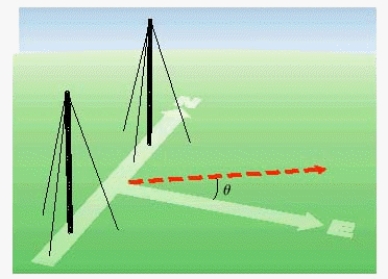 Approximate I in terms of I o for
Approximate I in terms of I o for 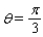 .
.
A)0.055I o
B)0.044I o
C)0.066I o
D)I o
E)0.033I o
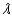 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 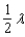 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 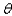 is given by
is given by 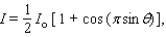 where I o is the maximum intensity.
where I o is the maximum intensity.  Approximate I in terms of I o for
Approximate I in terms of I o for 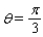 .
.A)0.055I o
B)0.044I o
C)0.066I o
D)I o
E)0.033I o

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
54
Refer to the graph of y = cos x to find the separate values of x in the interval 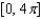 that satisfy the equation.
that satisfy the equation. 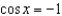
A)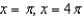
B)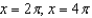
C)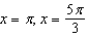
D)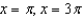
E)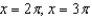
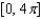 that satisfy the equation.
that satisfy the equation. 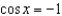
A)
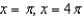
B)
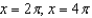
C)
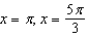
D)
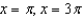
E)
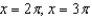

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
55
Use the graph of a trigonometric function to aid in sketching the graph of the equation without plotting points. 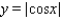
A)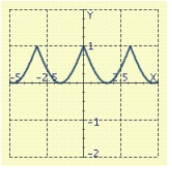
B)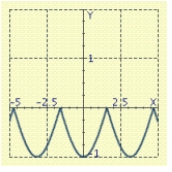
C)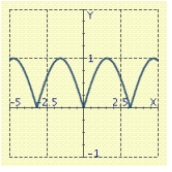
D)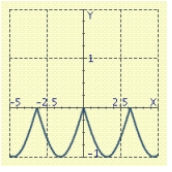
E)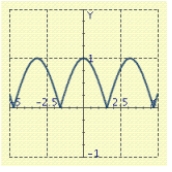
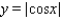
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
56
Find the amplitude, the period, and the phase shift. 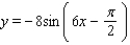
A)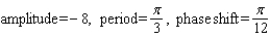
B)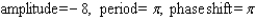
C)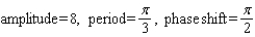
D)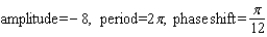
E)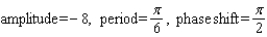
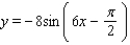
A)
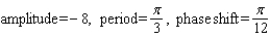
B)
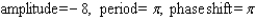
C)
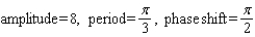
D)
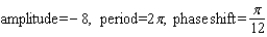
E)
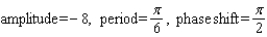

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
57
Express the angle as a decimal, to the nearest ten-thousandth of a degree. 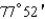
A)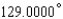
B)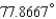
C)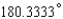
D)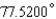
E)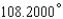
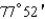
A)
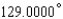
B)
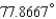
C)
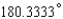
D)
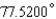
E)
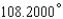

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
58
An airplane flying at a speed of 360 mi/hr flies from a point A in the direction 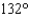 for 45 minutes and then flies in the direction
for 45 minutes and then flies in the direction 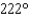 for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
A)764 mi
B)540 mi
C)180 mi
D)1 mi
E)382 mi
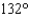 for 45 minutes and then flies in the direction
for 45 minutes and then flies in the direction 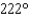 for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.A)764 mi
B)540 mi
C)180 mi
D)1 mi
E)382 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
59
Verify the identity by transforming the left-hand side into the right-hand side. 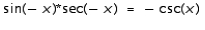
A)False
B)True
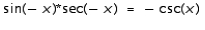
A)False
B)True

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
60
Find the quadrant containing  if the given conditions are true.
if the given conditions are true. 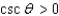 and
and 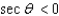
A)IV
B)III
C)II
D)I
 if the given conditions are true.
if the given conditions are true. 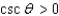 and
and 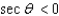
A)IV
B)III
C)II
D)I

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
61
A ship leaves port at 1:00 P.M. and sails in the direction 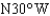 at a rate of 20 mi/hr. Another ship leaves port at 1:30 P.M. and sails in the direction
at a rate of 20 mi/hr. Another ship leaves port at 1:30 P.M. and sails in the direction 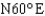 at a rate of 18 mi/hr. Approximately how far apart are the ships at 4:00 P.M.?
at a rate of 18 mi/hr. Approximately how far apart are the ships at 4:00 P.M.?
A)75 mi
B)150 mi
C)27 mi
D)81 mi
E)15 mi
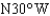 at a rate of 20 mi/hr. Another ship leaves port at 1:30 P.M. and sails in the direction
at a rate of 20 mi/hr. Another ship leaves port at 1:30 P.M. and sails in the direction 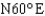 at a rate of 18 mi/hr. Approximately how far apart are the ships at 4:00 P.M.?
at a rate of 18 mi/hr. Approximately how far apart are the ships at 4:00 P.M.?A)75 mi
B)150 mi
C)27 mi
D)81 mi
E)15 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
62
Express the angle as a decimal, to the nearest ten-thousandth of a degree. 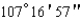
A)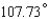
B)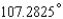
C)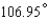
D)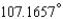
E)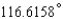
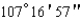
A)
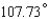
B)
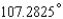
C)
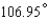
D)
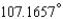
E)
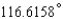

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
63
Points on the terminal sides of angles play an important part in the design of arms for robots. Suppose a robot has a straight arm 20 inches long that can rotate about the origin in a coordinate plane. If the robot's hand is located at (20, 0) and then rotates through an angle of 60 o , what is the new location of the hand?
A)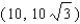
B)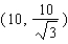
C)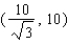
D)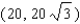
E)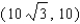
A)
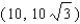
B)
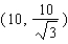
C)
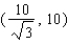
D)
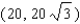
E)
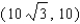

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
64
The amount of sunshine illuminating a wall of a building can greatly affect the energy efficiency of the building. The solar radiation striking a vertical wall that faces east is given by the formula 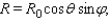 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 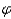 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with 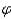 = 90 o when the sun is in the east and
= 90 o when the sun is in the east and 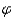 = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 60 o and the sun is in the southeast?
is equal to 60 o and the sun is in the southeast?
Round the answer to the nearest integer.
A)40 %
B)59 %
C)20 %
D)25 %
E)35 %
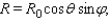 where R 0 is the maximum solar radiation possible,
where R 0 is the maximum solar radiation possible,  is the angle that the sun makes with the horizontal, and
is the angle that the sun makes with the horizontal, and 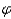 is the direction of the sun in the sky, with
is the direction of the sun in the sky, with 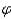 = 90 o when the sun is in the east and
= 90 o when the sun is in the east and 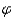 = 0 o when the sun is in the south. What percentage of R 0 is striking the wall when
= 0 o when the sun is in the south. What percentage of R 0 is striking the wall when  is equal to 60 o and the sun is in the southeast?
is equal to 60 o and the sun is in the southeast?Round the answer to the nearest integer.
A)40 %
B)59 %
C)20 %
D)25 %
E)35 %

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
65
Scientists sometimes use the formula 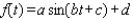 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in  , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 34
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 34  occurs at 2 P.M., and the average temperature of 19
occurs at 2 P.M., and the average temperature of 19  occurs 6 hours later.
occurs 6 hours later.
A)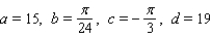
B)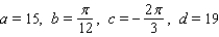
C)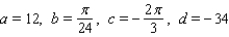
D)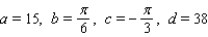
E)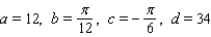
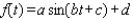 to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in
to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in  , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 34
, and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature of 34  occurs at 2 P.M., and the average temperature of 19
occurs at 2 P.M., and the average temperature of 19  occurs 6 hours later.
occurs 6 hours later.A)
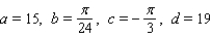
B)
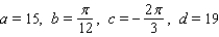
C)
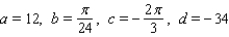
D)
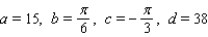
E)
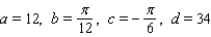

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
66
Approximate the acute angle  to the nearest
to the nearest 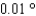 .
. 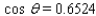
A)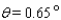
B)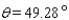
C)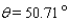
D)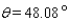
E)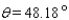
 to the nearest
to the nearest 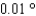 .
. 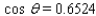
A)
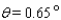
B)
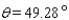
C)
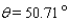
D)
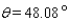
E)
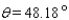

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
67
Find the amplitude, the period, and the phase shift. 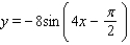
A)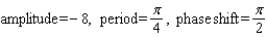
B)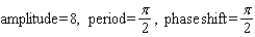
C)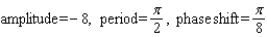
D)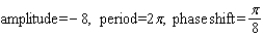
E)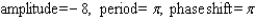
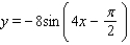
A)
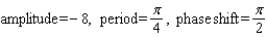
B)
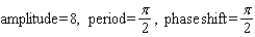
C)
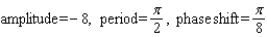
D)
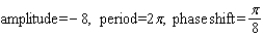
E)
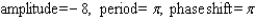

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
68
On a certain spring day with 12 hours of daylight, the light intensity I takes on its largest value of 400 calories/cm 2 at midday. If t = 0 corresponds to sunrise and t is measured in hours, find a formula I = a sin bt that fits this information.
A)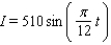
B)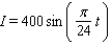
C)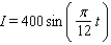
D)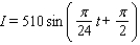
E)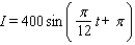
A)
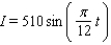
B)
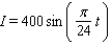
C)
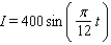
D)
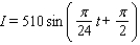
E)
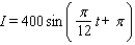

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
69
A CB antenna is located on the top of a garage that is 17 feet tall. From a point on level ground that is 120 feet from a point directly below the antenna, the antenna subtends an angle of 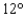 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 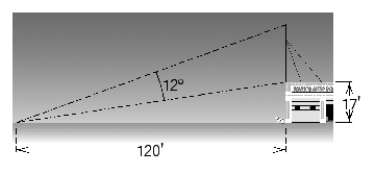
A)345.6 ft
B)36.8 ft
C)95.7 ft
D)24.2 ft
E)26.8 ft
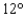 , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place.
, as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 
A)345.6 ft
B)36.8 ft
C)95.7 ft
D)24.2 ft
E)26.8 ft

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
70
A forester, 180 feet from the base of a redwood tree, observes that the angle between the ground and the top of the tree is 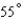 . Estimate the height of the tree.
. Estimate the height of the tree.
A)246.8 feet
B)257.1 feet
C)8,133.0 feet
D)265.7 feet
E)0.0 feet
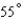 . Estimate the height of the tree.
. Estimate the height of the tree.A)246.8 feet
B)257.1 feet
C)8,133.0 feet
D)265.7 feet
E)0.0 feet

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
71
Find the period of the equation. 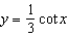
A)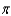
B)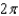
C)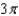
D)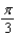
E)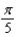
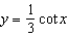
A)
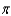
B)
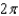
C)
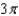
D)
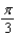
E)
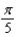

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
72
Approximate, to the nearest 0.01 radian, all angles  in the interval [ 0, 2
in the interval [ 0, 2 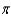 ) that satisfy the equation.
) that satisfy the equation. 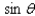 = 0.0135
= 0.0135
A)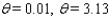
B)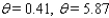
C)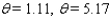
D)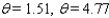
E)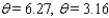
 in the interval [ 0, 2
in the interval [ 0, 2 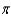 ) that satisfy the equation.
) that satisfy the equation. 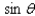 = 0.0135
= 0.0135A)
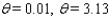
B)
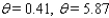
C)
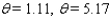
D)
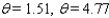
E)
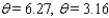

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
73
Find the exact values of the six trigonometric functions of the angle, whenever possible. 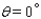
A)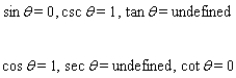
B)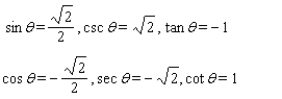
C)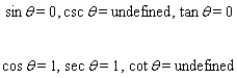
D)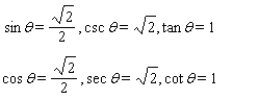
E)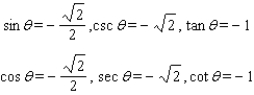
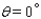
A)
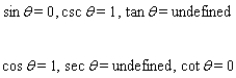
B)
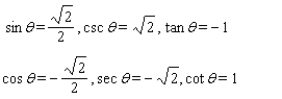
C)
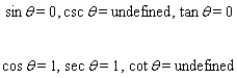
D)
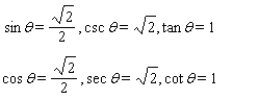
E)
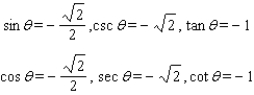

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
74
Use fundamental identities to find the exact values of the trigonometric functions for the given conditions. 
A)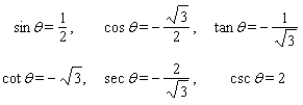
B)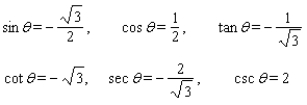
C)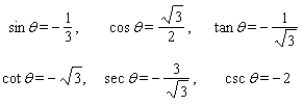
D)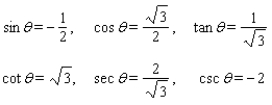
E)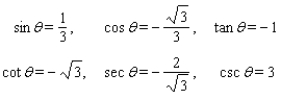

A)
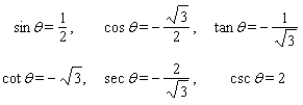
B)
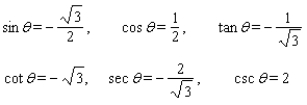
C)
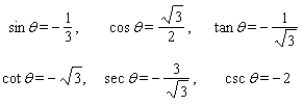
D)
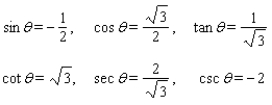
E)
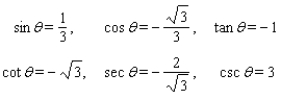

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
75
Approximate to four decimal places. 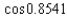
A)0.6569
B)0.6723
C)0.6059
D)0.6693
E)1.3386
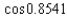
A)0.6569
B)0.6723
C)0.6059
D)0.6693
E)1.3386

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
76
The popular biorhythm theory uses the graphs of three simple sine functions to make predictions about an individual's physical, emotional, and intellectual potential for a particular day. The graphs are given by 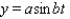 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 23 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 23 days.
A)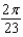
B)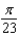
C)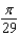
D)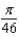
E)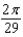
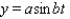 with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 23 days.
with t in days and t = 0 corresponding to birth. Find the value of b for the physical cycle, which has a period of 23 days.A)
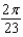
B)
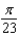
C)
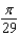
D)
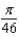
E)
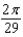

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
77
An airplane flying at a speed of 300 mi/hr flies from a point A in the direction 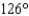 for 15 minutes and then flies in the direction
for 15 minutes and then flies in the direction 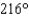 for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
A)474 mi
B)237 mi
C)213 mi
D)134 mi
E)300 mi
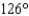 for 15 minutes and then flies in the direction
for 15 minutes and then flies in the direction 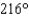 for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.A)474 mi
B)237 mi
C)213 mi
D)134 mi
E)300 mi

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
78
Radio stations often have more than one broadcasting tower because federal guidelines do not usually permit a radio station to broadcast its signal in all directions with equal power. Since radio waves can travel over long distances, it is important to control their directional patterns so that radio stations do not interfere with one another. Suppose that a radio station has two broadcasting towers located along a north-south line, as shown in the figure. If the radio station is broadcasting at a wavelength 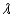 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 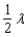 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 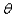 is given by
is given by 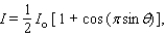 where I o is the maximum intensity.
where I o is the maximum intensity. 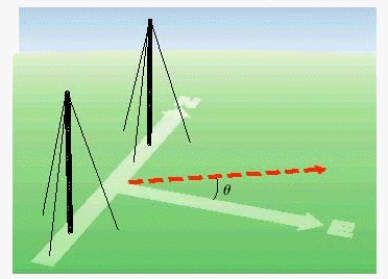 Approximate I in terms of I o for
Approximate I in terms of I o for 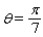 .
.
A)I o
B)0.614I o
C)0.625I o
D)0.603I o
E)0.592I o
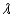 and the distance between the two radio towers is equal to
and the distance between the two radio towers is equal to 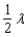 , then the intensity I of the signal in the direction
, then the intensity I of the signal in the direction 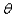 is given by
is given by 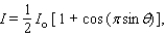 where I o is the maximum intensity.
where I o is the maximum intensity.  Approximate I in terms of I o for
Approximate I in terms of I o for 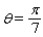 .
.A)I o
B)0.614I o
C)0.625I o
D)0.603I o
E)0.592I o

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
79
The phases of the moon can be described using the phase angle  , determined by the sun, the moon, and the Earth, as shown in the figure. Because the moon orbits Earth,
, determined by the sun, the moon, and the Earth, as shown in the figure. Because the moon orbits Earth,  changes during the course of a month. The area of the region A of the moon, which appears illuminated to an observer on Earth, is given by
changes during the course of a month. The area of the region A of the moon, which appears illuminated to an observer on Earth, is given by 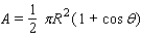 , where R = 1,080 mi is the radius of the moon. Approximate A for the following position of the moon:
, where R = 1,080 mi is the radius of the moon. Approximate A for the following position of the moon: 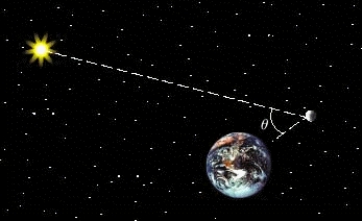
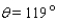
A)A = 943,920 mi 2
B)A = 3,434,635 mi 2
C)A = 1,151,699 mi 2
D)A = 3,533,300 mi 2
E)A = 3,775,680 mi 2
 , determined by the sun, the moon, and the Earth, as shown in the figure. Because the moon orbits Earth,
, determined by the sun, the moon, and the Earth, as shown in the figure. Because the moon orbits Earth,  changes during the course of a month. The area of the region A of the moon, which appears illuminated to an observer on Earth, is given by
changes during the course of a month. The area of the region A of the moon, which appears illuminated to an observer on Earth, is given by 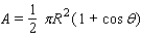 , where R = 1,080 mi is the radius of the moon. Approximate A for the following position of the moon:
, where R = 1,080 mi is the radius of the moon. Approximate A for the following position of the moon: 
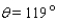
A)A = 943,920 mi 2
B)A = 3,434,635 mi 2
C)A = 1,151,699 mi 2
D)A = 3,533,300 mi 2
E)A = 3,775,680 mi 2

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
80
Use the graph of a trigonometric function to aid in sketching the graph of the equation without plotting points. 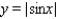
A)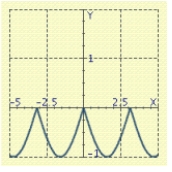
B)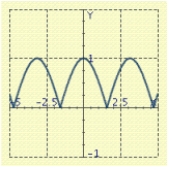
C)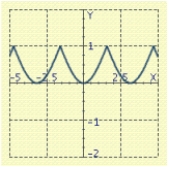
D)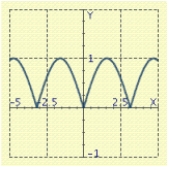
E)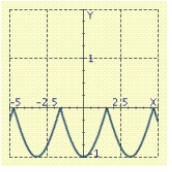
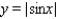
A)

B)

C)

D)

E)


Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck


