Deck 18: Mathematics in Engineering
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/50
Play
Full screen (f)
Deck 18: Mathematics in Engineering
1
Find an equation of the line through (1,-3) with a slope of 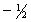 .
.
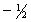 .
.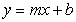
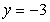
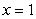
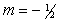
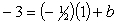
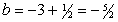
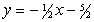
2
In general, engineering problems are mathematical models of physical situations.
True
3
Greek alphabetic characters quite commonly are used to express angles, dimensions, and physical variables in drawings and in mathematical equations and expressions.It is therefore very important to be familiar with these characters in order to communicate with other engineers.
True
4
Hooke's Law describes the relationship between force F and deflection x in a spring according to the following equation: 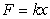 .Which type of mathematical model is used in Hooke's Law?
.Which type of mathematical model is used in Hooke's Law?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Logarithmic model
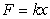 .Which type of mathematical model is used in Hooke's Law?
.Which type of mathematical model is used in Hooke's Law?A)Linear model
B)Nonlinear model
C)Exponential model
D)Logarithmic model

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
5
What is the name of the following Greek alphabetic character? 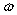
A)Omega
B)Mu
C)Gamma
D)Lambda
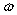
A)Omega
B)Mu
C)Gamma
D)Lambda

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
6
For nonlinear models (equations) the slope is constant.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
7
The quantity or numerical value within a linear model that shows by how much the dependent variable changes each time a change in the independent variable is introduced is known as
A)the x-intercept.
B)the y-intercept.
C)the dependent intercept.
D)the slope.
A)the x-intercept.
B)the y-intercept.
C)the dependent intercept.
D)the slope.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
8
In the spring equation F = k x, the spring force, F is called
A)a dependent variable
B)an independent variable
C)none of the above
A)a dependent variable
B)an independent variable
C)none of the above

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
9
What is the name of the following Greek alphabetic character? 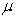
A)Omega
B)Mu
C)Gamma
D)Lambda
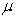
A)Omega
B)Mu
C)Gamma
D)Lambda

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
10
For many engineering situations, exponential and logarithmic models are used to describe the relationships between dependent and independent variables because they predict the actual relationships more accurately than linear models do.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
11
Mathematics is a language that has its own symbols and terminology.As an engineering student, you need to learn mathematical symbols and their meanings.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
12
Find an equation of the line that passes through the points (-1,2) and (3,-4).

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
13
Find an equation of the line through (5,2) that is perpendicular to the line 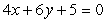 .
.
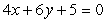 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
14
Find an equation of the line through (5,2) that is parallel to the line 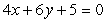 .
.
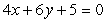 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
15
For many engineering situations, nonlinear models are used to describe the relationships between dependent and independent variables because they predict the actual relationships more accurately than linear models do.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
16
What is the name of the following Greek alphabetic character? 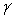
A)Epsilon
B)Zeta
C)Gamma
D)Lambda
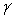
A)Epsilon
B)Zeta
C)Gamma
D)Lambda

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
17
In the spring equation F = k x, the deformation of the spring, x is called
A)a dependent variable
B)an independent variable
C)none of the above
A)a dependent variable
B)an independent variable
C)none of the above

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
18
The simplest form of models commonly used to describe a wide range of engineering situations is
A)linear equations.
B)nonlinear equations.
C)exponential equations.
D)logarithmic equations.
A)linear equations.
B)nonlinear equations.
C)exponential equations.
D)logarithmic equations.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
19
Find the slope of the line that passes thru the points (2,1) and (8,5).

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
20
The pitch of a roof refers to its "steepness" and is expressed in terms of the number of inches the roof rises for each 12 inches of run.For example, an 8-12 pitch means that the roof rises 8 inches vertically for each 12 inches of horizontal run.What is the slope of a roof with an 8-12 pitch?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
21
The path of flight (trajectory) of a football thrown by a quarterback is described by the following function: 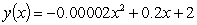 where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
How high above the ground is the football as it leaves the quarterback's hand?
A)0.002 m
B)0.2 m
C)2 m
D)7.7 m
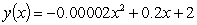 where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)How high above the ground is the football as it leaves the quarterback's hand?
A)0.002 m
B)0.2 m
C)2 m
D)7.7 m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
22
The term rate of change always refers to how a physical quantity varies with time.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
23
Solve the following set of equations using matrices: 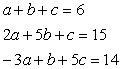
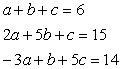

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
24
The path of flight (trajectory) of a football thrown by a quarterback is described by the following function: 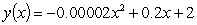 where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
How high above the ground is the football when it is 30 meters downfield from the quarterback?
A)1.1 m
B)2.2 m
C)28 m
D)7.9 m
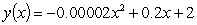 where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)
where y = vertical position of football relative to the ground (m) x = horizontal position of football relative to launch position (m)How high above the ground is the football when it is 30 meters downfield from the quarterback?
A)1.1 m
B)2.2 m
C)28 m
D)7.9 m

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
25
Solve the following set of equations using the Gaussian method: 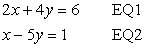
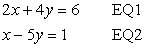

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
26
Given the following matrix: 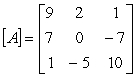 find
find 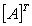 .
.
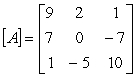 find
find 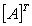 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
27
Given the following matrix: 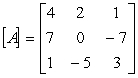 calculate the determinant of
calculate the determinant of 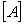 .
.
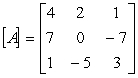 calculate the determinant of
calculate the determinant of 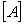 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
28
Calculate the average rate of change for the following functions: 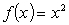 between
between 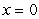 and
and 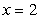
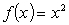 between
between 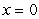 and
and 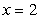

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
29
Calculate the average rate of change for the following function: 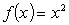 between
between 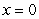 and
and 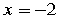
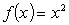 between
between 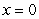 and
and 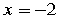

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
30
The velocity of an object under constant acceleration can be modeled using the following function: v(t) = v0 + at where v = velocity
V0 = initial velocity
A = acceleration
T = time
Which type of mathematical model is used to describe velocity in this application?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Logarithmic model
V0 = initial velocity
A = acceleration
T = time
Which type of mathematical model is used to describe velocity in this application?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Logarithmic model

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
31
Given the following matrix: 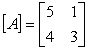 calculate the determinant of
calculate the determinant of 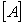 .
.
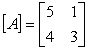 calculate the determinant of
calculate the determinant of 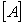 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
32
Perform the following operations on the given matrices: 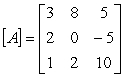
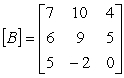
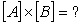
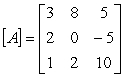
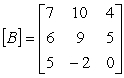
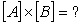

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
33
Calculus is commonly divided into two broad areas:
A)single variable and multivariable calculus.
B)differential and integral calculus.
C)vector and matrix calculus.
D)linear and nonlinear calculus.
A)single variable and multivariable calculus.
B)differential and integral calculus.
C)vector and matrix calculus.
D)linear and nonlinear calculus.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
34
The position of an object subjected to constant acceleration can be described by the following function: 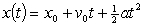 where
where 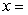 position (m)
position (m) 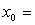 initial position (m)
initial position (m) 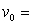 initial velocity (m/s)
initial velocity (m/s) 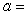 acceleration (m/s^2)
acceleration (m/s^2) 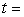 time (sec) Which type of mathematical model is used here to describe the object's position?
time (sec) Which type of mathematical model is used here to describe the object's position?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Trigonometric model
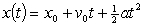 where
where 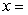 position (m)
position (m) 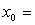 initial position (m)
initial position (m) 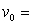 initial velocity (m/s)
initial velocity (m/s) 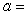 acceleration (m/s^2)
acceleration (m/s^2) 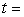 time (sec) Which type of mathematical model is used here to describe the object's position?
time (sec) Which type of mathematical model is used here to describe the object's position?A)Linear model
B)Nonlinear model
C)Exponential model
D)Trigonometric model

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
35
Perform the following operations on the given matrices: 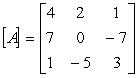
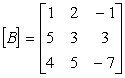
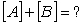
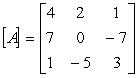
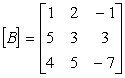
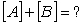

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
36
The rate of change refers to how a dependent variable changes with respect to an independent variable.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the average rate of change for the following function: 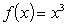 between
between 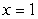 and
and 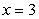
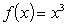 between
between 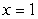 and
and 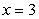

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
38
Perform the following operations on the given matrices: 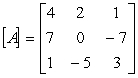
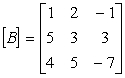
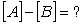
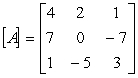
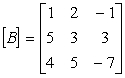
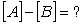

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
39
A company advertises a gadget at the regular price of $8, with a coupon for a second gadget at half price.The company sold 50 gadgets for a total of $364.How many coupons were redeemed?

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
40
The path of flight (trajectory) of a football thrown by a quarterback is described by the following function: 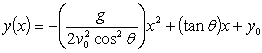 where y = vertical position of football relative to the ground y0 = vertical launch position of football relative to the ground
where y = vertical position of football relative to the ground y0 = vertical launch position of football relative to the ground
X = horizontal position of football relative to launch position
G = magnitude of gravitational acceleration
V0 = launch speed
Θ = launch angle relative to horizontal
Which type of mathematical model is used here to describe the football's trajectory?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Trigonometric model
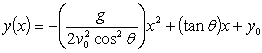 where y = vertical position of football relative to the ground y0 = vertical launch position of football relative to the ground
where y = vertical position of football relative to the ground y0 = vertical launch position of football relative to the groundX = horizontal position of football relative to launch position
G = magnitude of gravitational acceleration
V0 = launch speed
Θ = launch angle relative to horizontal
Which type of mathematical model is used here to describe the football's trajectory?
A)Linear model
B)Nonlinear model
C)Exponential model
D)Trigonometric model

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
41
Find the derivative of 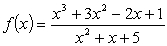 .
.
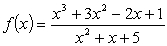 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
42
Find the derivative of 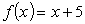 .
.
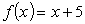 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate: 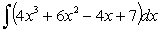
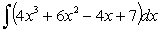

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
44
Find the derivative of 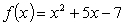 .
.
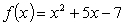 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
45
What kind of mathematical model contains derivatives of functions?
A)nonlinear equation
B)differential equation
C)exponential equation
D)logarithmic equation
A)nonlinear equation
B)differential equation
C)exponential equation
D)logarithmic equation

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
46
Boundary conditions provide information about what is happening physically at the boundaries of a problem.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate: 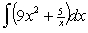
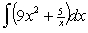

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
48
Many engineering problems are modeled using differential equations with a set of corresponding boundary and/or initial conditions.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
49
Initial conditions tell us about the initial conditions of a system (at time t = 0), before a disturbance or a change is introduced.

Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck
50
Find the derivative of 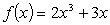 .
.
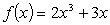 .
.
Unlock Deck
Unlock for access to all 50 flashcards in this deck.
Unlock Deck
k this deck


