Deck 4: Growth and Policy
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 4: Growth and Policy
1
Consider an economy whose production function is
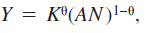 with A = 4 K / N. Suppose that it has a saving rate of.1, a population growth rate of.02, and an average depreciation rate of.03 and that
with A = 4 K / N. Suppose that it has a saving rate of.1, a population growth rate of.02, and an average depreciation rate of.03 and that
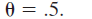
a. Reduce the production function to the form y = ak. What is a
b. What are the growth rates of output and capital in this model
c. Interpret a. What are we really saying when we assume that the labor-augmenting technology, A , is proportional to the level of capital per worker
d. What makes this an endogenous growth model
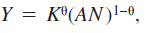 with A = 4 K / N. Suppose that it has a saving rate of.1, a population growth rate of.02, and an average depreciation rate of.03 and that
with A = 4 K / N. Suppose that it has a saving rate of.1, a population growth rate of.02, and an average depreciation rate of.03 and that 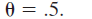
a. Reduce the production function to the form y = ak. What is a
b. What are the growth rates of output and capital in this model
c. Interpret a. What are we really saying when we assume that the labor-augmenting technology, A , is proportional to the level of capital per worker
d. What makes this an endogenous growth model
There is an economy with a given production function written as follows:
 .
.
The value of the technological parameter is four times the capital labor ratio. Suppose that the economy's rate of saving is 10 percent and the rate of population growth is 2 percent. In addition the rate of depreciation is 3 percent. Take the value of the capital share in income equal to 0.5.
To find the per capita production function, first replace the value of A and convert the production function in terms of capital only as follows:
 Find the output per head by substituting the values in the production function and dividing the aggregate production function with the augmented labor as follows:
Find the output per head by substituting the values in the production function and dividing the aggregate production function with the augmented labor as follows:
 Comparing the results with the output per head in general form, the value of 'a' turns out to be
Comparing the results with the output per head in general form, the value of 'a' turns out to be
 .
.
b)
The growth rate of output is determined by the expression
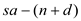 . This is found to be 0 percent as seen below:
. This is found to be 0 percent as seen below:
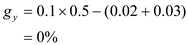 In the steady state, capital per worker does not grow and hence the growth rate of capital is zero.
In the steady state, capital per worker does not grow and hence the growth rate of capital is zero.
c)
The value of the variable 'a' turns out to be 2. This implies that if capital per worker is 5, then the technology parameter doubles the output per worker so determined. In the beginning, the labor augmenting technological progress was four times the capital per worker.
This implies that the technology increases the average productivity of labor by increasing the amount of capital per worker. Another way to approach this is that such a technology increases the efficiency of per head capita so that same capital per head is able to double the output
d)
Endogenous growth model advocates for the use of technology factor as a variable that is not exogenously given but is dependent and determined within the model. Here, in the given model, the technology is labor augmenting and there are constant returns to capital.
Hence, economy can sustain the economic growth by expanding the pool of knowledge.
 .
. The value of the technological parameter is four times the capital labor ratio. Suppose that the economy's rate of saving is 10 percent and the rate of population growth is 2 percent. In addition the rate of depreciation is 3 percent. Take the value of the capital share in income equal to 0.5.
To find the per capita production function, first replace the value of A and convert the production function in terms of capital only as follows:
 Find the output per head by substituting the values in the production function and dividing the aggregate production function with the augmented labor as follows:
Find the output per head by substituting the values in the production function and dividing the aggregate production function with the augmented labor as follows: Comparing the results with the output per head in general form, the value of 'a' turns out to be
Comparing the results with the output per head in general form, the value of 'a' turns out to be .
. b)
The growth rate of output is determined by the expression
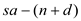 . This is found to be 0 percent as seen below:
. This is found to be 0 percent as seen below: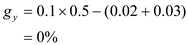 In the steady state, capital per worker does not grow and hence the growth rate of capital is zero.
In the steady state, capital per worker does not grow and hence the growth rate of capital is zero. c)
The value of the variable 'a' turns out to be 2. This implies that if capital per worker is 5, then the technology parameter doubles the output per worker so determined. In the beginning, the labor augmenting technological progress was four times the capital per worker.
This implies that the technology increases the average productivity of labor by increasing the amount of capital per worker. Another way to approach this is that such a technology increases the efficiency of per head capita so that same capital per head is able to double the output
d)
Endogenous growth model advocates for the use of technology factor as a variable that is not exogenously given but is dependent and determined within the model. Here, in the given model, the technology is labor augmenting and there are constant returns to capital.
Hence, economy can sustain the economic growth by expanding the pool of knowledge.
2
What is the difference between absolute and conditional convergence, as predicted by the neoclassical growth model Which seems to be occurring, empirically
The notion of absolute convergence states that economies with the same savings rate and rate of population growth will reach the same steady-state equilibrium if they have access to the same technology. The notion of conditional convergence states that economies that have access to the same technology and the same rate of population growth but different savings rates will reach steady-state equilibria at a different level of output per capita but have the same long-term economic growth rate. Empirical evidence tends to support the notion of conditional convergence across countries.
3
Can endogenous growth theory help explain international differences in growth rates If so, how If not, what can it help explain
Endogenous growth theory assumes that the steady-state growth rate of output is affected by the rate at which the factors of production are accumulated. Therefore, policies to stimulate the savings rate serve to increase the rate at which the capital stock is accumulated, which may, in turn, lead to a higher growth rate of output. While this notion may be important in explaining the growth rates of highly developed countries at the leading edge of technology, it cannot explain the differences in growth rates across poorer countries. For these countries, the notion of conditional convergence seems to be more applicable.
4
Suppose a society can invest in two types of capital-physical and human. How can its choice regarding the distribution of investment affect its long-term growth potential

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Consider once more the neoclassical model with a steady-state level of per capita output. Suppose a society can choose its rate of population growth. How can this choice affect the steady-state per capita output Could such a policy help the country avoid falling into a poverty trap
b. Now suppose we have an endogenous growth model. How will a lower population growth rate affect the society's long-term growth potential
b. Now suppose we have an endogenous growth model. How will a lower population growth rate affect the society's long-term growth potential

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
What elements of neoclassical and endogenous growth models can help us explain the remarkable growth of the group of countries known as the Asian Tigers

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
Does growth in per capita output, among both more and less industrialized countries, have the potential to increase indefinitely Explain.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
What is endogenous growth How do endogenous growth models differ from the neoclassical models of growth presented in Chapter 3

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
On the Bureau of Labor Statistics website ( www.bls.gov ) mouse over "International" under "Subject Areas." Click on "International Labor Comparisons." Scroll down the page to find "More Tools" and click on "Series Report." Enter the following four data series numbers, one on each line (press enter after each series number) in the box given: INU0002UK0, INU0025UK0, INU0024UK0, INU0005UK0. Click "Next" and select 1950 as the start year and 2011 as the end year.
a. Set up an EXCEL file from the manufacturing data given between 1950-2011. Shown below is what series each series number corresponds to:
INU0002UK0: Manufacturing Output Index
INU0025UK0: Manufacturing Average Hours Index
INU0024UK0: Manufacturing Employment Index
INU0005UK0: Manufacturing Output per Hour Index
These indexes give us the evolution of output, hours, and employment in the manufacturing sector. For example, if the manufacturing output index increased from 110.0 in 2003 to 112.1 in 2004, one can conclude that manufacturing output rose by 1.9 percent in 2004 [(112.1 2 110.0)/110.0 3 100].
b. What happened to manufacturing output, employment, and average hours worked by an employee in the period 1950-2011 What factors could lead to an increase in total manufacturing output, while employment and average hours worked fell considerably
a. Set up an EXCEL file from the manufacturing data given between 1950-2011. Shown below is what series each series number corresponds to:
INU0002UK0: Manufacturing Output Index
INU0025UK0: Manufacturing Average Hours Index
INU0024UK0: Manufacturing Employment Index
INU0005UK0: Manufacturing Output per Hour Index
These indexes give us the evolution of output, hours, and employment in the manufacturing sector. For example, if the manufacturing output index increased from 110.0 in 2003 to 112.1 in 2004, one can conclude that manufacturing output rose by 1.9 percent in 2004 [(112.1 2 110.0)/110.0 3 100].
b. What happened to manufacturing output, employment, and average hours worked by an employee in the period 1950-2011 What factors could lead to an increase in total manufacturing output, while employment and average hours worked fell considerably

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Consider a two-sector model of growth, with two kinds of investment opportunities-one with a diminishing marginal product and one with a constant marginal product. ( Hint: See Figure 4-2.)
a. What does the production function for this problem look like
b. Characterize the set of equilibria for this model. Does output in any of the equilibria have nonzero per capita growth
c. What can this model help us explain that strict endogenous and neoclassical growth models cannot
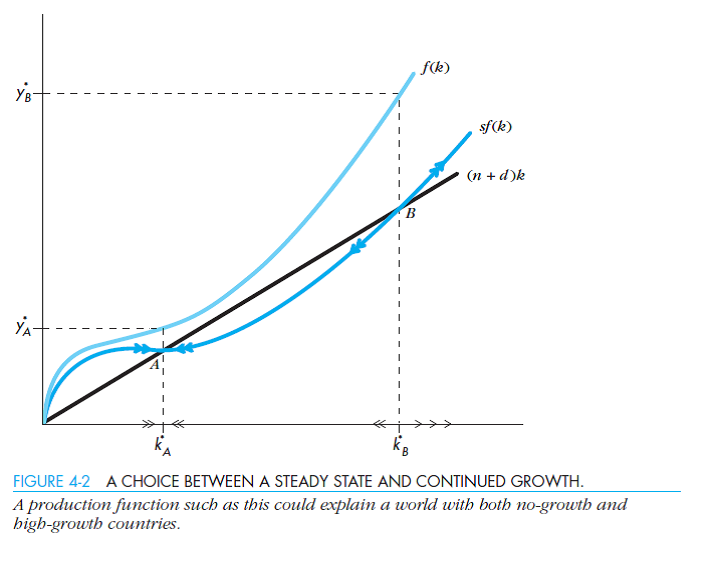
a. What does the production function for this problem look like
b. Characterize the set of equilibria for this model. Does output in any of the equilibria have nonzero per capita growth
c. What can this model help us explain that strict endogenous and neoclassical growth models cannot


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
Why doesn't the constant marginal product of capital assumed in this chapter's simple model of endogenous growth create a situation in which a single large firm dominates the economy, as traditional microeconomic reasoning would suggest

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
Now suppose we have a one-sector model with a variable rate of population growth. ( Hint: See Figure 4-3.)
a. What does the investment requirement line look like for this model
b. Characterize the set of equilibria, being sure to discuss their stability or lack thereof. Does output in any of these equilibria have nonzero per capita growth
c. Suppose your country is in a "poverty trap"-at the equilibrium with the very lowest level of output per person. What could the country do to move toward a point with higher income
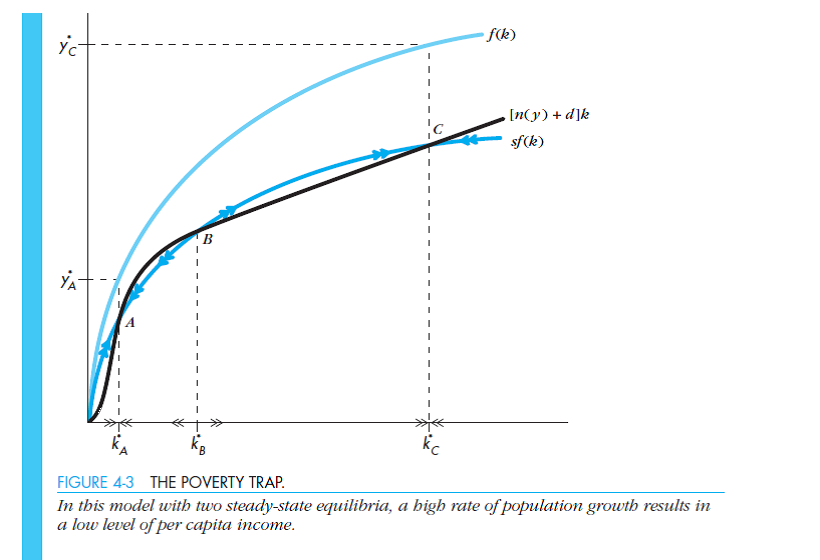
a. What does the investment requirement line look like for this model
b. Characterize the set of equilibria, being sure to discuss their stability or lack thereof. Does output in any of these equilibria have nonzero per capita growth
c. Suppose your country is in a "poverty trap"-at the equilibrium with the very lowest level of output per person. What could the country do to move toward a point with higher income


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
How do the implications of an increase in saving with regard to both the level and the growth rate of output differ between the neoclassical growth model outlined in Chapter 3 and the basic endogenous growth model outlined in this chapter

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose you add a variable rate of population growth to a two-sector model of growth. ( Hint: Combine Figures 4-2 and 4-3.)
a. What do the production function, investment requirement line, and saving line look like
b. Characterize the set of equilibria for this model. Does output in any of the equilibria have nonzero per capita growth
c. Does the addition of the variable rate of population growth to this model help you explain anything that a simpler two-sector model with a fixed rate of growth, or a one-sector model with variable population growth, cannot
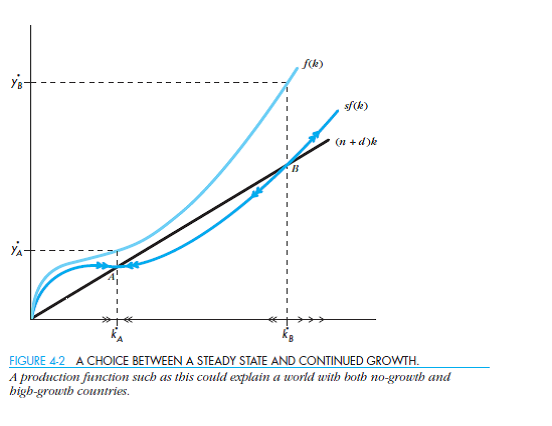
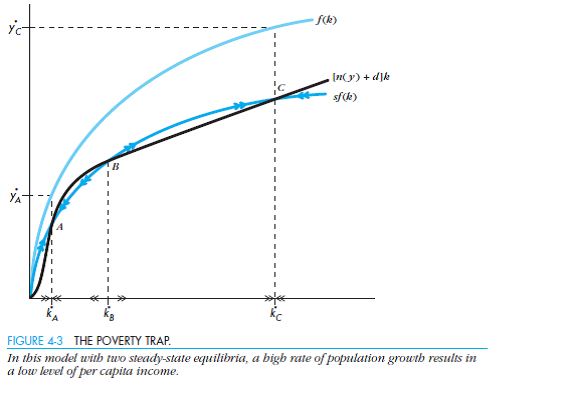
a. What do the production function, investment requirement line, and saving line look like
b. Characterize the set of equilibria for this model. Does output in any of the equilibria have nonzero per capita growth
c. Does the addition of the variable rate of population growth to this model help you explain anything that a simpler two-sector model with a fixed rate of growth, or a one-sector model with variable population growth, cannot



Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
(Optional)
a. What sorts of capital investment does this chapter suggest are most useful for explaining long-run equilibrium growth
b. Discuss the long-run growth potential of each of the following government programs:
i. Investment tax credits
ii. R D subsidies and grants
iii. Policies intended to increase saving
iv. Increased funding for primary education
a. What sorts of capital investment does this chapter suggest are most useful for explaining long-run equilibrium growth
b. Discuss the long-run growth potential of each of the following government programs:
i. Investment tax credits
ii. R D subsidies and grants
iii. Policies intended to increase saving
iv. Increased funding for primary education

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


