Deck 16: Oscillatory Motion
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 16: Oscillatory Motion
1
A torsional pendulum consists of a solid disk (mass = 2.0 kg, radius = 1.0 m) suspended by a wire attached to a rigid support. The body oscillates about the support wire. If the torsion constant is 16 N.m/rad, what is the angular frequency (in rad/s)? 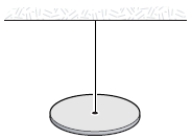
A)2
B)4
C)6
D)8
E)7

A)2
B)4
C)6
D)8
E)7
4
2
A body oscillates with simple harmonic motion along the x axis. Its displacement varies with time according to the equation x = 5 sin ( t + /3). The phase (in rad) of the motion at t = 2 s is:
A)7 /3.
B)( /3.)
C)( )
D)5 /3.
E)2
A)7 /3.
B)( /3.)
C)( )
D)5 /3.
E)2
7 /3.
3
Refer to Exhibit 16-1 below.Exhibit 16-1 A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below. 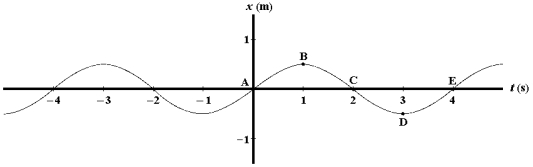 The point at which the object has negative velocity and zero acceleration is:
The point at which the object has negative velocity and zero acceleration is:
A)A
B)B
C)C
D)D
E)E
 The point at which the object has negative velocity and zero acceleration is:
The point at which the object has negative velocity and zero acceleration is:A)A
B)B
C)C
D)D
E)E
C
4
In the figure below, a hoop (radius R = 1.0 m, mass = 2.0 kg) having four spokes of negligible mass is suspended from a pivot a distance d = .25 m above its centre of mass. The angular frequency (in rad/s) for small oscillations is approximately: 
A)4.0.
B)2.5.
C)1.5.
D)1.0.
E)0.5.

A)4.0.
B)2.5.
C)1.5.
D)1.0.
E)0.5.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
A hoop, a solid cylinder, and a solid sphere all have the same mass m and the same radius R. Each is mounted to oscillate about an axis a distance 0.5 R from the centre. The axis is perpendicular to the circular plane of the hoop and the cylinder and to an equatorial plane of the sphere as shown below. Which is the correct ranking in order of increasing angular frequency ? 
A)hoop, cylinder, sphere
B)cylinder, sphere, hoop
C)sphere, cylinder, hoop
D)hoop, sphere, cylinder
E)sphere, hoop, cylinder

A)hoop, cylinder, sphere
B)cylinder, sphere, hoop
C)sphere, cylinder, hoop
D)hoop, sphere, cylinder
E)sphere, hoop, cylinder

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
In the figure below, a disk (radius R = 1.0 m, mass = 2.0 kg) is suspended from a pivot a distance d = 0.25 m above its centre of mass. For a circular disk, 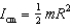 . The angular frequency (in rad/s) for small oscillations is approximately:
. The angular frequency (in rad/s) for small oscillations is approximately: 
A)4.2.
B)2.1.
C)1.5.
D)1.0.
E)3.8.
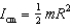 . The angular frequency (in rad/s) for small oscillations is approximately:
. The angular frequency (in rad/s) for small oscillations is approximately: 
A)4.2.
B)2.1.
C)1.5.
D)1.0.
E)3.8.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and released, it oscillates between positions A and B. Which statement about the system consisting of the spring and the mass is correct? 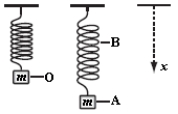
A)The gravitational potential energy of the system is greatest at A.
B)The elastic potential energy of the system is greatest at O.
C)The rate of change of momentum has its greatest magnitude at A and B.
D)The rate of change of gravitational potential energy is smallest at O.
E)The rate of change of gravitational potential energy has its greatest magnitude at A and B.

A)The gravitational potential energy of the system is greatest at A.
B)The elastic potential energy of the system is greatest at O.
C)The rate of change of momentum has its greatest magnitude at A and B.
D)The rate of change of gravitational potential energy is smallest at O.
E)The rate of change of gravitational potential energy has its greatest magnitude at A and B.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
A horizontal plank (m = 2.0 kg, L = 1.0 m) is pivoted at one end. A spring (k = 1.0 * 103 N/m) is attached at the other end, as shown in the figure. Find the angular frequency (in rad/s) for small oscillations. 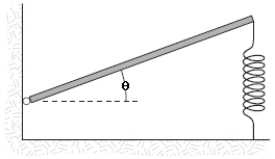
A)39
B)44
C)55
D)66
E)25

A)39
B)44
C)55
D)66
E)25

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
Two circus clowns (each having a mass of 50 kg) swing on two flying trapezes (negligible mass, length 25 m) shown in the figure. At the peak of the swing, one grabs the other, and the two swing back to one platform. The time for the forward and return motion is: 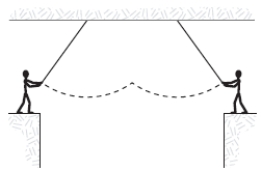
A)10 s.
B)50 s.
C)15 s.
D)20 s.
E)25 s.

A)10 s.
B)50 s.
C)15 s.
D)20 s.
E)25 s.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
Refer to Exhibit 16-1 below.Exhibit 16-1 A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below. 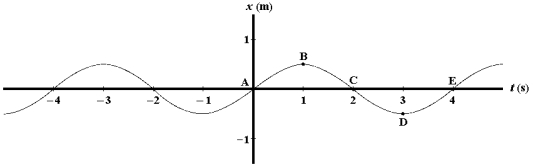 The point at which the object has zero velocity and positive acceleration is:
The point at which the object has zero velocity and positive acceleration is:
A)A
B)B
C)C
D)D
E)E
 The point at which the object has zero velocity and positive acceleration is:
The point at which the object has zero velocity and positive acceleration is:A)A
B)B
C)C
D)D
E)E

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
A body oscillates with simple harmonic motion along the x axis. Its displacement varies with time according to the equation x = 5.0 sin ( t + /3). The velocity (in m/s) of the body at t = 1.0 s is:
A)+7.9.
B)(-7.9.)
C)(-14.)
D)+14.
E)(-5.0.)
A)+7.9.
B)(-7.9.)
C)(-14.)
D)+14.
E)(-5.0.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
Three pendulums with strings of the same length and bobs of the same mass are pulled out to angles 1, 2 and 3 respectively and released. The approximation sin = holds for all three angles, with 3 > 2 > 1. How do the angular frequencies of the three pendulums compare?
A)( 3 > 2 > 1)
B)Need to know amplitudes to answer this question.
C)Need to know to answer this question.
D)( 1 > 2 > 3)
E)( 1 = 2 = 3)
A)( 3 > 2 > 1)
B)Need to know amplitudes to answer this question.
C)Need to know to answer this question.
D)( 1 > 2 > 3)
E)( 1 = 2 = 3)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
An object of mass m is attached to string of length L. When it is released from point A, the object oscillates between points A and B. Which statement about the system consisting of the pendulum and the Earth is correct? 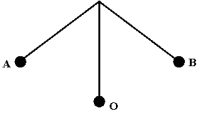
A)The gravitational potential energy of the system is greatest at A and B.
B)The kinetic energy of mass m is greatest at point O.
C)The greatest rate of change of momentum occurs at A and B.
D)All of the above are correct.
E)Only (a) and (b) above are correct.

A)The gravitational potential energy of the system is greatest at A and B.
B)The kinetic energy of mass m is greatest at point O.
C)The greatest rate of change of momentum occurs at A and B.
D)All of the above are correct.
E)Only (a) and (b) above are correct.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
The motion of a particle connected to a spring is described by x = 10 sin ( t). At what time (in s) is the potential energy equal to the kinetic energy?
A)0
B)0.25
C)0.50
D)0.79
E)1.0
A)0
B)0.25
C)0.50
D)0.79
E)1.0

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
The mass in the figure below slides on a frictionless surface. When the mass is pulled out, spring 1 is stretched a distance x1 from its equilibrium position and spring 2 is stretched a distance x2. The spring constants are k1 and k2 respectively. The force pulling back on the mass is: 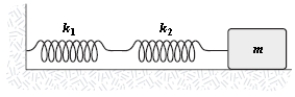
A)(-k2x1.)
B)(-k2x2.)
C)(-(k1x1 + k2x2).)
D) .
E) .

A)(-k2x1.)
B)(-k2x2.)
C)(-(k1x1 + k2x2).)
D) .
E) .

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
A body of mass 5.0 kg is suspended by a spring, which stretches 10 cm when the mass is attached. It is then displaced downward an additional 5.0 cm and released. Its position as a function of time is approximately:
A)y = -0.10 sin 9.9t.
B)y = 0.10 cos 9.9t.
C)y = -0.10 cos (9.9t + .1).
D)y = 0.10 sin (9.9t + 5).
E)y = -0.05 cos 9.9t.
A)y = -0.10 sin 9.9t.
B)y = 0.10 cos 9.9t.
C)y = -0.10 cos (9.9t + .1).
D)y = 0.10 sin (9.9t + 5).
E)y = -0.05 cos 9.9t.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
A uniform rod (mass m = 1.0 kg and length L = 2.0 m) pivoted at one end oscillates in a vertical plane as shown below. The period of oscillation (in s) is approximately: 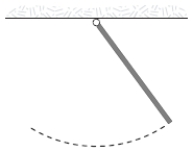
A)4.0.
B)1.6.
C)3.2.
D)2.3.
E)2.0.

A)4.0.
B)1.6.
C)3.2.
D)2.3.
E)2.0.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
The figure shows a uniform rod (length L = 1.0 m, mass = 2.0 kg) suspended from a pivot a distance d = 0.25 m above its centre of mass. The angular frequency (in rad/s) for small oscillations is approximately: 
A)1.0.
B)2.5.
C)1.5.
D)4.1.
E)3.5.

A)1.0.
B)2.5.
C)1.5.
D)4.1.
E)3.5.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
The amplitude of a system moving with simple harmonic motion is doubled. The total energy will then be:
A)4 times as large.
B)3 times as large.
C)2 times as large.
D)the same as it was.
E)half as much.
A)4 times as large.
B)3 times as large.
C)2 times as large.
D)the same as it was.
E)half as much.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
Refer to Exhibit 16-1 below.Exhibit 16-1 A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below. 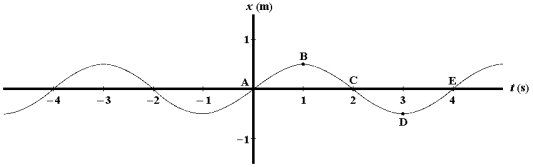 A point or points at which the object has positive velocity and zero acceleration is(are):
A point or points at which the object has positive velocity and zero acceleration is(are):
A)B
B)C
C)D
D)B and D
E)A and E
 A point or points at which the object has positive velocity and zero acceleration is(are):
A point or points at which the object has positive velocity and zero acceleration is(are):A)B
B)C
C)D
D)B and D
E)A and E

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
The oscillation of the 2.0-kg mass on a spring is described by where x is in centimetres and t is in seconds. What is the force constant of the spring?
A)4.0 N/m
B)0.80 N/m
C)16 N/m
D)32 N/m
E)2.0 N/m
A)4.0 N/m
B)0.80 N/m
C)16 N/m
D)32 N/m
E)2.0 N/m

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
In an inertia balance, a body supported against gravity executes simple harmonic oscillations in a horizontal plane under the action of a set of springs. If a 1.00 kg body vibrates at 1.00 Hz, a 2.00 kg body will vibrate at:
A)0.500 Hz.
B)0.707 Hz.
C)1.00 Hz.
D)1.41 Hz.
E)2.00 Hz.
A)0.500 Hz.
B)0.707 Hz.
C)1.00 Hz.
D)1.41 Hz.
E)2.00 Hz.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
A 2-m long 6 kg ladder pivoted at the top hangs down from a platform at the circus. A 42 kg trapeze artist climbs to a point where her centre of mass is at the centre of the ladder and swings at the system's natural frequency. The angular frequency (in s-1) of the system of ladder and woman is:
A)1.01.
B)3.07.
C)4.03.
D)8.05.
E)16.2.
A)1.01.
B)3.07.
C)4.03.
D)8.05.
E)16.2.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
At sea level, at a latitude where , a pendulum that takes 2.00 s for a complete swing back and forth has a length of 0.993 m. What is the value of g in m/s2 at a location where the length of such a pendulum is 0.970 m?
A)0.098 3
B)3.05
C)9.57
D)10.0
E)38.3
A)0.098 3
B)3.05
C)9.57
D)10.0
E)38.3

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
The mat of a trampoline is held by 32 springs, each having a spring constant of 5000 N/m. A person with a mass of 40.0 kg jumps from a platform 1.93 m high onto the trampoline. Determine the stretch of each of the springs.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
To double the total energy of a mass oscillating at the end of a spring with amplitude A, we need to:
A)increase the angular frequency by .
B)increase the amplitude by .
C)increase the amplitude by 2.
D)increase the angular frequency by 2.
E)increase the amplitude by 4 and decrease the angular frequency by .
A)increase the angular frequency by .
B)increase the amplitude by .
C)increase the amplitude by 2.
D)increase the angular frequency by 2.
E)increase the amplitude by 4 and decrease the angular frequency by .

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
John says that the value of the function cos[ (t + T) + ], obtained one period T after time t, is greater than cos( t + ) by 2 . Larry says that it is greater by the addition of 1.00 to cos( t + ). Which one, if either, is correct?
A)John, because T = 2 .
B)John, because T = 1 radian.
C)Larry, because T = 2 .
D)Larry, because T = 1 radian.
E)Neither, because cos( + 2 ) = cos .
A)John, because T = 2 .
B)John, because T = 1 radian.
C)Larry, because T = 2 .
D)Larry, because T = 1 radian.
E)Neither, because cos( + 2 ) = cos .

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
The motion of a piston in a car engine is simple harmonic. If the piston travels back and forth over a distance of 10 cm, and the piston has a mass of 1.5 kg, what is the maximum speed of the piston and the maximum force acting on the piston when the engine is running at 4200 rpm?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
Simple harmonic oscillations can be modelled by the projection of circular motion at constant angular velocity onto a diameter of the circle. When this is done, the analogue along the diameter of the acceleration of the particle executing simple harmonic motion is:
A)the displacement from the centre of the diameter of the projection of the position of the particle on the circle.
B)the projection along the diameter of the velocity of the particle on the circle.
C)the projection along the diameter of tangential acceleration of the particle on the circle.
D)the projection along the diameter of centripetal acceleration of the particle on the circle.
E)meaningful only when the particle moving in the circle also has a non-zero tangential acceleration.
A)the displacement from the centre of the diameter of the projection of the position of the particle on the circle.
B)the projection along the diameter of the velocity of the particle on the circle.
C)the projection along the diameter of tangential acceleration of the particle on the circle.
D)the projection along the diameter of centripetal acceleration of the particle on the circle.
E)meaningful only when the particle moving in the circle also has a non-zero tangential acceleration.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
Which of the following combinations of variables results in the greatest period for a pendulum?
A)length = L, mass = M, and maximum angular displacement = 3 degrees
B)length = 2L, mass = M/2, and maximum angular displacement = 1 degree
C)length = 1.5L, mass = 2M, and maximum angular displacement = 2 degrees
D)length = L, mass =
M, and maximum angular displacement =
degrees
E)length = L, mass = 4M, and maximum angular displacement = 4 degrees
A)length = L, mass = M, and maximum angular displacement = 3 degrees
B)length = 2L, mass = M/2, and maximum angular displacement = 1 degree
C)length = 1.5L, mass = 2M, and maximum angular displacement = 2 degrees
D)length = L, mass =
M, and maximum angular displacement =
degrees
E)length = L, mass = 4M, and maximum angular displacement = 4 degrees

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
An ore car of mass 4000 kg starts from rest and rolls downhill on tracks from an outback mine. A spring with k = 400 000 N/m is located at the end of the tracks. At the spring's maximum compression, the car is at an elevation 10 m lower than its elevation at the starting point. How much is the spring compressed in stopping the ore car? Ignore friction.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
When a damping force is applied to a simple harmonic oscillator which has period T0 in the absence of damping, the new period T is such that:
A)T < T0.
B)T = T0.
C)T > T0.
D)( T < T0.)
E)( T > 0T0.)
A)T < T0.
B)T = T0.
C)T > T0.
D)( T < T0.)
E)( T > 0T0.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
Ellen says that whenever the acceleration is directly proportional to the displacement of an object from its equilibrium position, the motion of the object is simple harmonic motion. Mary says this is true only if the acceleration is opposite in direction to the displacement. Which one, if either, is correct?
A)Ellen, because 2 is directly proportional to the constant multiplying the displacement and to the mass.
B)Ellen, because 2 is directly proportional to the mass.
C)Mary, because 2 is directly proportional to the constant multiplying the displacement and to the mass.
D)Mary, because 2 is directly proportional to the mass.
E)Mary, because the second derivative of an oscillatory function like sin( t) or cos( t) is always proportional to the negative of the original function.
A)Ellen, because 2 is directly proportional to the constant multiplying the displacement and to the mass.
B)Ellen, because 2 is directly proportional to the mass.
C)Mary, because 2 is directly proportional to the constant multiplying the displacement and to the mass.
D)Mary, because 2 is directly proportional to the mass.
E)Mary, because the second derivative of an oscillatory function like sin( t) or cos( t) is always proportional to the negative of the original function.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
An automobile (m = 1.00 * 103 kg) is driven into a brick wall in a safety test. The bumper behaves like a spring (k = 5.00 *106 N/m), and is observed to compress a distance of 3.16 cm as the car is brought to rest. What was the initial speed of the automobile?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
A damped oscillator is released from rest with an initial displacement of 10.00 cm. At the end of the first complete oscillation the displacement reaches 9.05 cm. When 4 more oscillations are completed, what is the displacement reached?
A)7.41 cm
B)6.71 cm
C)6.07 cm
D)5.49 cm
E)5.25 cm
A)7.41 cm
B)6.71 cm
C)6.07 cm
D)5.49 cm
E)5.25 cm

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
An archer pulls her bow string back 0.40 m by exerting a force that increases uniformly from zero to 240 N. What is the equivalent spring constant of the bow, and how much work is done in pulling the bow?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Refer to Exhibit 16-1 below.Exhibit 16-1 A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below. 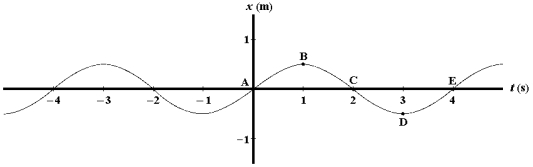 The point at which the object has zero velocity and negative acceleration is:
The point at which the object has zero velocity and negative acceleration is:
A)A
B)B
C)C
D)D
E)E
 The point at which the object has zero velocity and negative acceleration is:
The point at which the object has zero velocity and negative acceleration is:A)A
B)B
C)C
D)D
E)E

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
When a damping force is applied to a simple harmonic oscillator which has angular frequency 0 in the absence of damping, the new angular frequency is such that:
A)( < 0.)
B)( = 0.)
C)( > 0.)
D)( T < 0T0.)
E)( T > 0T0.)
A)( < 0.)
B)( = 0.)
C)( > 0.)
D)( T < 0T0.)
E)( T > 0T0.)

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


