Deck 1: Physics and Measurement
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/27
Play
Full screen (f)
Deck 1: Physics and Measurement
1
You are trying to compare the fuel efficiency of two cars, one made in the US and one made in Australia. You know that the Australian car will use 14 litres of fuel per 100 km of driving. The US car has been tested as getting 10 miles per gallon of fuel used. A mile is 1.609 km and a US gallon is 3.785 litres. How many litres will the US car use per 100 km of driving?
A)23.5
B)14.5
C)14.0
D)13.2
E)10.0
A)23.5
B)14.5
C)14.0
D)13.2
E)10.0
23.5
2
Which one of the quantities below has dimensions equal to ?
A)mv
B)mv2
C)
D)mrv
E)
A)mv
B)mv2
C)
D)mrv
E)
C
3
The term occurs in Bernoulli's equation in Chapter 15, with being the density of a fluid and v its speed. The dimensions of this term are:
A)M-1L5T2
B)MLT2
C)ML-1T-2
D)M-1L9T-2
E)M-1L3T-2
A)M-1L5T2
B)MLT2
C)ML-1T-2
D)M-1L9T-2
E)M-1L3T-2
C
4
At a recent sporting event, an athlete ran a distance of 100±0.2 m in a time of 9.8±0.1 seconds. What was their speed?
A)10.20±0.2 m/s
B)10.20±0.3 m/s
C)10.20±0.01 m/s
D)10.20±0.12 m/s
E)10.20±0.05 m/s
A)10.20±0.2 m/s
B)10.20±0.3 m/s
C)10.20±0.01 m/s
D)10.20±0.12 m/s
E)10.20±0.05 m/s

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
5
The equation for the change of position of a train starting at x = 0 m is given by . The dimensions of b are:
A)T-3
B)LT-3
C)LT-2
D)LT-1
E)L-1T-1
A)T-3
B)LT-3
C)LT-2
D)LT-1
E)L-1T-1

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
6
Spike claims that dimensional analysis shows that the correct expression for change in velocity is , is , where m is mass, t is time, and F is the magnitude of force. Carla says that can't be true because the dimensions of force are . Which one, if either, is correct?
A)Spike, because .
B)Spike, because .
C)Carla, because .
D)Carla, because .
E)Spike, because the dimensions of force are .
A)Spike, because .
B)Spike, because .
C)Carla, because .
D)Carla, because .
E)Spike, because the dimensions of force are .

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
7
John and Linda are arguing about the definition of density. John says the density of an object is proportional to its mass. Linda says the object's mass is proportional to its density and to its volume. Which one, if either, is correct?
A)They are both wrong.
B)John is correct, but Linda is wrong.
C)John is wrong, but Linda is correct.
D)They are both correct.
E)They are free to redefine density as they wish.
A)They are both wrong.
B)John is correct, but Linda is wrong.
C)John is wrong, but Linda is correct.
D)They are both correct.
E)They are free to redefine density as they wish.

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
8
At the end of a year, a motor car company announces that sales of a pickup are down 43% for the year. If sales continue to decrease by 43% in each succeeding year, how long will it take for sales to decrease to zero?
A)1 year
B)2 years
C)3 years
D)4 years
E)More than 4 years
A)1 year
B)2 years
C)3 years
D)4 years
E)More than 4 years

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
9
Which quantity can be converted to the SI system by the conversion factor? ?
A)kilometers per hour
B)metres per second
C)miles per hour
D)kilometres per second
E)kilometers per minute
A)kilometers per hour
B)metres per second
C)miles per hour
D)kilometres per second
E)kilometers per minute

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following quantities has the same dimensions as kinetic energy, ? Note: [a] = [g] = LT-2; [h] = L and [v] = LT-1.
A)ma
B)mvx
C)mvt
D)mgh
E)mgt
A)ma
B)mvx
C)mvt
D)mgh
E)mgt

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
11
When doing a physics problem, you were asked to calculate how fast a car was going in a particular situation. You came up with an answer of 230 m/s. You want to check if this is plausible, by converting this number into more familiar units: kilometres per hour. What is 230 m/s when converted into kilometres per hour, and is this a plausible speed for a car?
A)230 km/hr: not plausible
B)828 km/hr: not plausible
C)64 km/hr: plausible
D)2.3 km/hr: plausible
E)23 km/hr: plausible
A)230 km/hr: not plausible
B)828 km/hr: not plausible
C)64 km/hr: plausible
D)2.3 km/hr: plausible
E)23 km/hr: plausible

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
12
The quantity with the same units as force times time, Ft, with dimensions MLT-1 is:
A)mv
B)mvr
C)mv2r
D)ma
E)
A)mv
B)mvr
C)mv2r
D)ma
E)

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
13
One mole of the carbon-12 isotope contains 6.022 *1023 atoms. What volume in m3 would be needed to store one mole of cube-shaped children's blocks 2.00 cm long on each side?
A)4.8 * 1018
B)1.2 *1022
C)6.0 * 1023
D)1.2 * 1024
E)4.8 *1024
A)4.8 * 1018
B)1.2 *1022
C)6.0 * 1023
D)1.2 * 1024
E)4.8 *1024

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
14
Five people measure the length of a car. The values they obtain are 2.38 m, 2.36 m, 2.41 m, 2.36 m and 2.37 m. What is the approximate uncertainty in their measurement of the length of the car?
A)5 cm
B)1 m
C)1 cm
D)0.01 cm
E)0.5 cm
A)5 cm
B)1 m
C)1 cm
D)0.01 cm
E)0.5 cm

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
15
You measure the height of a building using your knowledge of trigonometry, by measuring the angle to the top of the building from a point on the ground 100.0 m away. 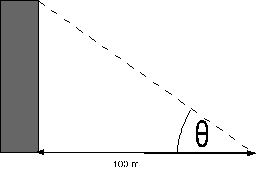 You measure an angle θ=20.0°±1.0°. How high is the building?
You measure an angle θ=20.0°±1.0°. How high is the building?
A)36.4±1.0 m
B)36.4±2.0 m
C)36.4±0.5 m
D)36.4±3.0 m
E)36.4±3.6 m
 You measure an angle θ=20.0°±1.0°. How high is the building?
You measure an angle θ=20.0°±1.0°. How high is the building?A)36.4±1.0 m
B)36.4±2.0 m
C)36.4±0.5 m
D)36.4±3.0 m
E)36.4±3.6 m

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
16
Two rocket engineers are trying to see whether a changed nozzle design makes their rockets go faster. The first rocket travels at a speed of 1000±3 m/s, while the second rocket travels at a speed of 1005±2 m/s. How much faster is the second rocket?
A)5±2 m/s
B)5±3 m/s
C)5±4 m/s
D)5±5 m/s
E)5±6 m/s
A)5±2 m/s
B)5±3 m/s
C)5±4 m/s
D)5±5 m/s
E)5±6 m/s

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
17
A standard exam page is 210 mm by 297 mm. An exam that is 2.0 mm thick has a volume of:
A)1.9 * 104 mm3.
B)4.7 *104 mm3.
C)1.2 * 105 mm3.
D)3.1* 105 mm3.
E)3.1 * 103 mm3.
A)1.9 * 104 mm3.
B)4.7 *104 mm3.
C)1.2 * 105 mm3.
D)3.1* 105 mm3.
E)3.1 * 103 mm3.

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
18
The density of an object is defined as:
A)the volume occupied by each unit of mass.
B)the amount of mass for each unit of volume.
C)the weight of each unit of volume.
D)the amount of the substance that has unit volume and unit mass.
E)the amount of the substance that contains as many particles as 12 grams of the carbon-12 isotope.
A)the volume occupied by each unit of mass.
B)the amount of mass for each unit of volume.
C)the weight of each unit of volume.
D)the amount of the substance that has unit volume and unit mass.
E)the amount of the substance that contains as many particles as 12 grams of the carbon-12 isotope.

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
19
The answer to a question is [MLT-1]. The question is 'What are the dimensions of:
A)mr?'
B)mvr?'
C)ma?'
D)mat?'
E) ?'
A)mr?'
B)mvr?'
C)ma?'
D)mat?'
E) ?'

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following products of ratios gives the conversion factors to convert metres per second to parsecs per year ? A parsec is a unit of distance used in astrophysics, and is equal to 3.26 light years. A light year is 9.46 x 1015 m.
A)
B)
C)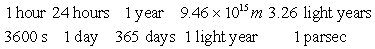
D)
E)
A)
B)
C)
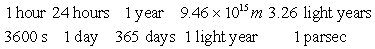
D)
E)

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
21
The basic function of a carburettor of an automobile is to atomise the petrol and mix it with air to promote rapid combustion. As an example, assume that 30 cm3 of petrol is atomised into N spherical droplets, each with a radius of 2.0 *10-5 m. What is the total surface area of these N spherical droplets?

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
22
If each frame of a motion picture film is 35 cm high, and 24 frames go by in a second, estimate how many frames are needed to show a two-hour-long movie.
A)1400
B)25 000
C)50 000
D)170 000
E)This cannot be determined without knowing how many reels were used.
A)1400
B)25 000
C)50 000
D)170 000
E)This cannot be determined without knowing how many reels were used.

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
23
A 2.00 m by 3.00 m plate of aluminium has a mass of 324 kg. What is the thickness of the plate? (The density of aluminium is 2.70 *103 kg/m3.)

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
24
A rectangle has a length of 1.323 m and a width of 4.16 m. Using significant figure rules, what is the area of this rectangle?
A)5.503 68 m2
B)5.503 7 m2
C)5.504 m2
D)5.50 m2
E)5.5 m2
A)5.503 68 m2
B)5.503 7 m2
C)5.504 m2
D)5.50 m2
E)5.5 m2

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
25
One number has three significant figures and another number has four significant figures. If these numbers are added, subtracted, multiplied, or divided, which operation can produce the greatest number of significant figures?
A)the addition
B)the subtraction
C)the multiplication
D)the division
E)All the operations result in the same number of significant figures.
A)the addition
B)the subtraction
C)the multiplication
D)the division
E)All the operations result in the same number of significant figures.

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
26
The standard kilogram is a platinum-iridium cylinder 39 mm in height and 39 mm in diameter. What is the density of the material?

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck
27
What is the mass of air in a room that measures 5.0 m * 8.0 m *3.0 m? (The density of air is 1/800 that of water).

Unlock Deck
Unlock for access to all 27 flashcards in this deck.
Unlock Deck
k this deck


