Deck 9: Sequences, Series, and Probability

Question 1

The probability that a basketball player will make a given free throw is $\frac { 7 } { 10 }$ . To find the probability that the player makes exactly 8 out of her next 10 free throws, evaluate the term
​ ${ } _ { 10 } C _ { 8 } \left( \frac { 7 } { 10 } \right) ^ { 8 } \left( \frac { 3 } { 10 } \right) ^ { 2 }$ in the expansion of $\left( \frac { 7 } { 10 } + \frac { 3 } { 10 } \right) ^ { 10 }$ . Round to four decimal places.
​

Answer 1

0.2335

Question 2

Use the Binomial Theorem to expand and simplify the expression.
​ $2 ( x - 4 ) ^ { 4 } + 5 ( x - 4 ) ^ { 2 }$ ​

Answer 2

$2 x ^ { 4 } - 32 x ^ { 3 } + 197 x ^ { 2 } - 552 x + 592$

Question 3

Find the probability for the experiment of tossing a six-sided die twice.
​
The sum is at least 6.
​

Answer 3

$\frac { 5 } { 12 }$

Question 4

A study of the effectiveness of a flu vaccine was conducted with a sample of 469 people. Some participants in the study were given no vaccine, some were given one injection, and some were given two injections. The results of the study are listed in the table.
$$\begin{array} { | l | l | l | l | l | } \hline & \text { No vaccine } & \text { One injection } & \text { Two injections } & \text { Total } \\\hline \text { Flu } & 5 & 5 & 15 & 25 \\\hline \text { No flu } & 140 & 44 & 260 & 444 \\\hline \text { Total } & 145 & 49 & 275 & 469 \\\hline\end{array}$$ A person is selected at random from the sample. Find the specified probability that the person got the flu and had one injection. Round your answer to one decimal place.

Question 5

The numbers 1, 2, 3, 4, 5, 6 are to be arranged. How many different arrangements are possible under the condition that all even numbers come first?
​

Question 6

Find pk + 1 for the given pk .
​ $p _ { k } = \frac { k ^ { 2 } ( k + 3 ) ^ { 2 } } { 6 }$ ​

Question 7

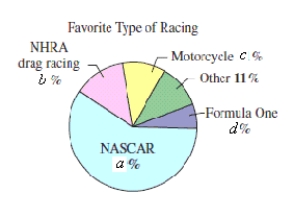
The figure shows the results of a survey in which auto racing fans listed their favorite type of racing. What is the probability that an auto racing fan selected at random does not list NHRA drag racing as his or her favorite type of racing? ( $a = 61 \%$ , $b=15 \%$ , $c = 9 \%$ , $d = 4 \%$ )
​ ​

Question 8

Find the sum of the finite geometric sequence.
​ $\sum _ { n = 1 } ^ { 7 } 6 ^ { n - 1 }$ ​

Question 9

Use the Binomial Theorem to expand and simplify the expression.
​ $( y - 4 ) ^ { 5 }$ ​

Question 10

Eight cards are chosen at random from a standard deck of playing cards. In how many ways can the cards be chosen if all eight cards are hearts.

Question 11

Find the number of diagonals of a undecagon (11 sides). (A line segment connecting any two nonadjacent vertices is called a diagonal of the polygon.)

Question 12

Evaluate ${ } _ { n } C _ { r }$ using the formula from this section.
​ ${ } _ { 54 } C _ { 5 }$ ​

Question 13

Use sigma notation to write the sum.
​ $\frac { 1 } { 6 ( 1 ) } + \frac { 1 } { 6 ( 2 ) } + \frac { 1 } { 6 ( 3 ) } + \ldots + \frac { 1 } { 6 ( 9 ) }$ ​

Question 14

Seven cards are chosen at random from a standard deck of playing cards. In how many ways can the cards be chosen if all seven cards are the same suit.

Question 15

Write the first five terms of the arithmetic sequence defined recursively.
​ $a _ { 1 } = 15$ , $a _ { n + 1 } = a _ { n } + 6$ ​