Deck 8: Systems of Equations and Inequalities
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 8: Systems of Equations and Inequalities
1
Find the sales necessary to break even (R =
C) for the cost C of producing x units and the revenue R obtained by selling x units. (Round to the nearest whole unit.)
,
C) for the cost C of producing x units and the revenue R obtained by selling x units. (Round to the nearest whole unit.)
,
180 units
2
Find x and y.
x = 2, y = 5
3
Write the partial fraction decomposition of the rational expression.
4
Use a graphing utility to solve the system of equations. Find the solution(s) accurate to two decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Solve the system of linear equations and check any solution algebraically.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
A large region of forest has been infested with gypsy moths. The region is roughly triangular, as shown in the figure on the next page. From the northernmost vertex A of the region, the distances to the other vertices are x = 25 miles south and 10 miles east (for vertex
B), and 20 miles south and 28 miles east (for vertex
C). Use a graphing utility to approximate the number of square miles in this region.
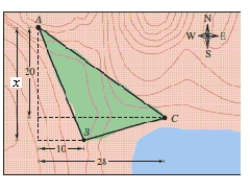
B), and 20 miles south and 28 miles east (for vertex
C). Use a graphing utility to approximate the number of square miles in this region.


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
Use a determinant and the given vertices of a triangle to find the area of the triangle.
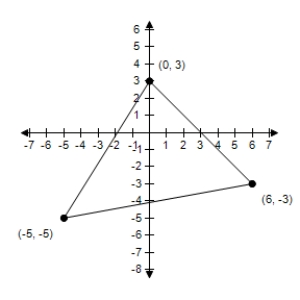


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
Solve the system graphically.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
Use a graphing utility and Cramer's Rule to solve (if possible) the system of equations.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Find values of x, y, and λ that satisfy the system. These systems arise in certain optimization problems in calculus, and λ is called a Lagrange multiplier.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
Write the matrix in reduced row-echelon form.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
Find the maximum value of the objective function and where it occurs, subject to the constraints:
Objective function:
Constraints:
Objective function:
Constraints:

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
Find the consumer surplus and producer surplus.
Demand
Supply
Demand
Supply

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
According to automobile association of a country, on March 27, 2009, the national average price per gallon of regular unleaded (85-octane) gasoline was $2.09, and the price of premium unleaded (92-octane) gasoline was $2.24. Write an objective function that models the cost of the blend of mid-grade unleaded gasoline (90-octane).

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
Find the sales necessary to break even (R - C = 0) for the cost C of producing x units and the revenue R obtained by selling x units. (Round to the nearest whole unit.)

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


