Deck 6: Analytic Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 6: Analytic Trigonometry
1
Use the product-to-sum formulas to rewrite the product as a sum or difference.
2
Use the sum-to-product formulas to rewrite the sum or difference as a product.
3
Evaluate the following expression.
4
4
Use the Quadratic Formula to solve the given equation on the interval ; then use a graphing utility to approximate the angle x. Round answers to three decimal places.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Find the expression as the sine or cosine of an angle.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
Evaluate the following expression. ( , where n is a whole number)

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
Convert the expression.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
Find the exact value of the given expression.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
Use the figure to find the exact value of the trigonometric function.
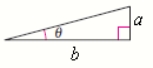 ,
,
 ,
, 
Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Simplify the expression algebraically.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
Find the exact value of .

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
Convert the expression.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
Use inverse functions where needed to find all solutions of the equation in the interval .

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
Use the product-to-sum formulas to rewrite the product as a sum or difference.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
Use the cofunction identities to evaluate the expression without using a calculator.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


