Deck 5: Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/45
Play
Full screen (f)
Deck 5: Probability
1
Moosy-Woosy Airlines flies between Moose Bay and Moose Lake Alaska. In many
airports, nearby flocking birds can present problems during takeoffs and landings. In
Alaska, the problem is moose. If a moose is spotted in the immediate area of the
runway, a takeoff or landing must be delayed until the moose is very carefully
escorted away. Of the 1200 takeoffs and landings in a recent 12-month period at
Moose Bay, there were 75 moose delays. Based on this long series of observations,
what is the estimated probability that the 1201st takeoff or landing attempt will be
delayed by a moose sighting?
airports, nearby flocking birds can present problems during takeoffs and landings. In
Alaska, the problem is moose. If a moose is spotted in the immediate area of the
runway, a takeoff or landing must be delayed until the moose is very carefully
escorted away. Of the 1200 takeoffs and landings in a recent 12-month period at
Moose Bay, there were 75 moose delays. Based on this long series of observations,
what is the estimated probability that the 1201st takeoff or landing attempt will be
delayed by a moose sighting?
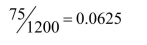
2
The event "A or B" consists of all of the outcomes that are in both of the
events.
events.
False
3
False
4
The collection of possible outcomes of a chance experiment is called the
sample space of the experiment.
sample space of the experiment.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
5
As discussed in the text, the classical approach to probability has a serious limitation
that is overcome by the relative frequency approach. What is the limitation?
that is overcome by the relative frequency approach. What is the limitation?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
6
The Addition Rule states that for any two events, 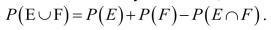
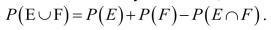

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
7
Arctic Plains Planes Airlines flies in Alaska between Prudhoe Bay and Deadhorse.
APPA has only one small plane, and passengers have a choice between sitting in one
of two first class seats, one of four second class seats, and the co-pilot's seat. (APPA
airlines also has only one pilot.) If the seats are assigned at random, what is the
probability that a passenger will be assigned a second class seat?
APPA has only one small plane, and passengers have a choice between sitting in one
of two first class seats, one of four second class seats, and the co-pilot's seat. (APPA
airlines also has only one pilot.) If the seats are assigned at random, what is the
probability that a passenger will be assigned a second class seat?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
8
The Multiplication Rule states that for any two events, 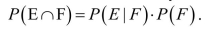
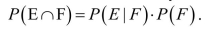

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
9
In a few sentences, describe the difference between the intersection of two events and
the union of two events
the union of two events

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
10
As discussed in the text, the classical approach to probability has a serious limitation
that is overcome by the relative frequency approach. What is the limitation?
that is overcome by the relative frequency approach. What is the limitation?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
11
In a few sentences, define the following terms:
a) Event
b) Chance experiment
a) Event
b) Chance experiment

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
12
Two events are said to be mutually exclusive if they can't occur at the
same time.
same time.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
13
The probability of an event E can always be computed using the formula, 


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
14
Anna is a child who has just turned 2 years old, and she has entered the "terrible
two's" stage of human development. She has discovered that if she drops her spoon
on the floor, her parents will pick it up and return it to her. By actual count halfway
through her second year, there have been 900 spoon retrievals. Out of these, 315
times the spoon has landed in the "up" position on the floor. Based on this long series
of observations, what is the estimated probability that her 901st spoon drop will land
in the "up" position?
two's" stage of human development. She has discovered that if she drops her spoon
on the floor, her parents will pick it up and return it to her. By actual count halfway
through her second year, there have been 900 spoon retrievals. Out of these, 315
times the spoon has landed in the "up" position on the floor. Based on this long series
of observations, what is the estimated probability that her 901st spoon drop will land
in the "up" position?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
15
Anna is an engineer on vacation with a problem. S he is driving in Halifax, Nova
Scotia, and is stopped at an intersection. She could drive to Wolfville, Truro, or
Antigonish. She does not have a preference, and decides make her decision by
flipping two coins. If two heads appear, she will go to Wolfville, if two tails she will
go to Antigonish. What is the probability she will go to Truro?
Scotia, and is stopped at an intersection. She could drive to Wolfville, Truro, or
Antigonish. She does not have a preference, and decides make her decision by
flipping two coins. If two heads appear, she will go to Wolfville, if two tails she will
go to Antigonish. What is the probability she will go to Truro?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
16
An event, by definition, consists of exactly one outcome.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
17
It is possible for two mutually exclusive events to be independent.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
18
If two events, A and B, are mutually exclusive, then 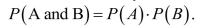
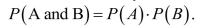

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
19
In a few sentences, define the following terms:
a) Simple event
b) Sample space
a) Simple event
b) Sample space

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
20
A chance experiment is the process of making an observation when there
is uncertainty concerning which of two or more possible outcomes will
result.
is uncertainty concerning which of two or more possible outcomes will
result.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
21
Experimental studies use blinding to prevent researchers from biasing their measurements of the subjects. In a study of a drug intervention, a clinician who was
"blinded" was asked to guess what treatment each subject received. Data from that
experiment are shown below. Suppose a person is to be chosen at random from the
subjects in this study.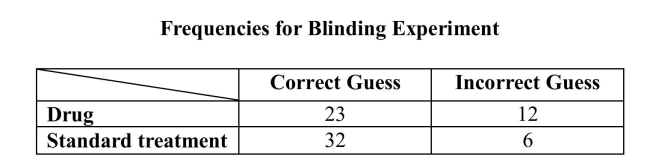 a) What is the probability that the clinician made a correct guess for the selected
a) What is the probability that the clinician made a correct guess for the selected
subject?
b) What is the probability the selected subject received the drug treatment?
c) What is the probability the selected subject will be one for whom the clinician
correctly guessed as having received drug treatment?
d) What is the probability the selected subject will be one for whom the clinician
guessed correctly or who received the standard treatment?
e) What is the probability the selected subject will be one for whom the clinician
guessed correctly and who received the standard treatment?
f) In a few sentences, explain why the probabilities calculated in parts (d) and (e)
differ.
"blinded" was asked to guess what treatment each subject received. Data from that
experiment are shown below. Suppose a person is to be chosen at random from the
subjects in this study.
 a) What is the probability that the clinician made a correct guess for the selected
a) What is the probability that the clinician made a correct guess for the selectedsubject?
b) What is the probability the selected subject received the drug treatment?
c) What is the probability the selected subject will be one for whom the clinician
correctly guessed as having received drug treatment?
d) What is the probability the selected subject will be one for whom the clinician
guessed correctly or who received the standard treatment?
e) What is the probability the selected subject will be one for whom the clinician
guessed correctly and who received the standard treatment?
f) In a few sentences, explain why the probabilities calculated in parts (d) and (e)
differ.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
22
At Beth & Mary's Ice Cream Emporium customers always choose one topping to
sprinkle on their ice cream. The toppings are classified as either candy (C) or fruit
(F) toppings. Consider the chance experiment where the choice of toppings -- (C) or
(F) -- is recorded for each of the next two customers who order ice cream.
a) List all the outcomes in the sample space.
b) Using your sample space in part (a), list the outcomes in each of the following
events.
A = the event that both customers pick a candy topping
B = the event that both customers pick the same type of topping
C = the event that at least one customer picks a candy topping
A:
B:
C:
sprinkle on their ice cream. The toppings are classified as either candy (C) or fruit
(F) toppings. Consider the chance experiment where the choice of toppings -- (C) or
(F) -- is recorded for each of the next two customers who order ice cream.
a) List all the outcomes in the sample space.
b) Using your sample space in part (a), list the outcomes in each of the following
events.
A = the event that both customers pick a candy topping
B = the event that both customers pick the same type of topping
C = the event that at least one customer picks a candy topping
A:
B:
C:

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
23
At the State Fair the rifle range offers 4 different hats as prizes for perfect scores, one
hat for each of the State University campuses. The hats are in boxes. When someone
gets a perfect score, a box is chosen at random and given to that person. No
substitutions are allowed. A local football fan (an ace shot who never misses) wishes
to collect all 4 hat designs. There are a very large number of hats on hand and there
are equal numbers of each hat design, so each design has a probability of 0.25 of
being the prize at any given time. You are to design a simulation that could be used
to estimate the average number of perfect scores needed to get a complete the set of
hats.
a) To simulate this strategy, assign digits to the hat designs that will result in the
probability of selection of each design being 0.25. b) Describe how you would use a random digit table to conduct one run of your
b) Describe how you would use a random digit table to conduct one run of your
simulation. Hint: one run continues until a complete set of the 4 hats is acquired.
c) Using the following lines from a random number table, demonstrate how your
assignment of digits in part (a) would be used to carry out one run of the
simulation. (You may mark above the digits to help explain your procedure.) d) Suppose that the rifle range manager decides to order different numbers of hats,
d) Suppose that the rifle range manager decides to order different numbers of hats,
consistent with the popularity of each campus's football team. Hat 1 will be put
in 50% of the boxes, Hats 2 and 3 will each be put in 20% of the boxes, and Hat 4
will be put in 10% of the boxes. Assign digits to the hats in a way that will be
consistent with these probabilities. e) Perform three runs, and use your results to estimate the probability that it would
e) Perform three runs, and use your results to estimate the probability that it would
take more than 10 boxes to complete the set of 4 hats. (You may mark above the
digits to help explain your procedure.)
hat for each of the State University campuses. The hats are in boxes. When someone
gets a perfect score, a box is chosen at random and given to that person. No
substitutions are allowed. A local football fan (an ace shot who never misses) wishes
to collect all 4 hat designs. There are a very large number of hats on hand and there
are equal numbers of each hat design, so each design has a probability of 0.25 of
being the prize at any given time. You are to design a simulation that could be used
to estimate the average number of perfect scores needed to get a complete the set of
hats.
a) To simulate this strategy, assign digits to the hat designs that will result in the
probability of selection of each design being 0.25.
 b) Describe how you would use a random digit table to conduct one run of your
b) Describe how you would use a random digit table to conduct one run of yoursimulation. Hint: one run continues until a complete set of the 4 hats is acquired.
c) Using the following lines from a random number table, demonstrate how your
assignment of digits in part (a) would be used to carry out one run of the
simulation. (You may mark above the digits to help explain your procedure.)
 d) Suppose that the rifle range manager decides to order different numbers of hats,
d) Suppose that the rifle range manager decides to order different numbers of hats,consistent with the popularity of each campus's football team. Hat 1 will be put
in 50% of the boxes, Hats 2 and 3 will each be put in 20% of the boxes, and Hat 4
will be put in 10% of the boxes. Assign digits to the hats in a way that will be
consistent with these probabilities.
 e) Perform three runs, and use your results to estimate the probability that it would
e) Perform three runs, and use your results to estimate the probability that it wouldtake more than 10 boxes to complete the set of 4 hats. (You may mark above the
digits to help explain your procedure.)


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
24
What is the probability that the selected official is a Strategoi, given that this person
lives outside Metro Athens?
lives outside Metro Athens?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
25
Understanding attitudes of humans towards wildlife is an important step in learning how to work with people on wildlife issues. Coyotes have expanded their range throughout the continental United States, even in the Washington, DC area. The data below are from a survey of George Mason University undergraduate students.
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.
What is the probability that the selected official is from Metro Athens, given that this person is a Tamaiai?
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.What is the probability that the selected official is from Metro Athens, given that this person is a Tamaiai?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
26
Experimental studies in psychology use blinding to prevent researchers from biasing their measurements of subjects in the study. In a study of a psychotherapeutic
intervention, a blinded clinician was asked to guess what treatment each subject
received. Data from that experiment are shown below. Suppose a subject is to be
chosen at random from the subjects in this study.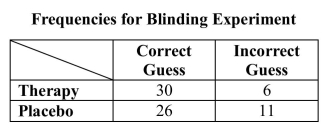 a) What is the probability that the clinician made a correct guess for the selected
a) What is the probability that the clinician made a correct guess for the selected
subject?
b) What is the probability the selected subject will have had therapy?
c) What is the probability the selected subject will be one for whom the clinician
correctly guessed had therapy?
d) What is the probability the selected subject will be one for whom the clinician
guessed correctly or who received the placebo treatment?
e) What is the probability the selected subject will be one for whom the clinician
guessed correctly and who received the placebo treatment?
f) In a few sentences, explain why the probabilities calculated in parts (d) and (e)
differ.
intervention, a blinded clinician was asked to guess what treatment each subject
received. Data from that experiment are shown below. Suppose a subject is to be
chosen at random from the subjects in this study.
 a) What is the probability that the clinician made a correct guess for the selected
a) What is the probability that the clinician made a correct guess for the selectedsubject?
b) What is the probability the selected subject will have had therapy?
c) What is the probability the selected subject will be one for whom the clinician
correctly guessed had therapy?
d) What is the probability the selected subject will be one for whom the clinician
guessed correctly or who received the placebo treatment?
e) What is the probability the selected subject will be one for whom the clinician
guessed correctly and who received the placebo treatment?
f) In a few sentences, explain why the probabilities calculated in parts (d) and (e)
differ.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
27
Students in two classes of upper-level mathematics were classified according to class
standing and gender, resulting in the following table.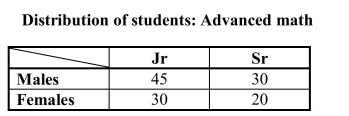 One of these students will be selected at random. Define events A,
One of these students will be selected at random. Define events A,
B, and C as follows:
A = the event that the selected student is a female
B = the event that the selected student is a male
C = the event that the selected student is a senior.
For each pair of events in the following table, indicate whether the two events are
disjoint and/or independent by putting a Y or N in each of the cells.
standing and gender, resulting in the following table.
 One of these students will be selected at random. Define events A,
One of these students will be selected at random. Define events A,B, and C as follows:
A = the event that the selected student is a female
B = the event that the selected student is a male
C = the event that the selected student is a senior.
For each pair of events in the following table, indicate whether the two events are
disjoint and/or independent by putting a Y or N in each of the cells.


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
28
Understanding attitudes of humans towards wildlife is an important step in learning how to work with people on wildlife issues. Coyotes have expanded their range throughout the continental United States, even in the Washington, DC area. The data below are from a survey of George Mason University undergraduate students.
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.
What is the probability that the selected official is from the Strategoi?
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.What is the probability that the selected official is from the Strategoi?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
29
Black bears (Ursus americanus) have a tendency to wander looking for food, and
they have a high level of curiosity. These characteristics will sometimes get them
into trouble when they travel through national parks. When they become "nuisances,"
the Park Service transplants them to other areas if possible. Data on the gender of
transplanted bears and the outcome of the transplant for bears transplanted in Glacier
National Park over a 10-year period are given in the table below.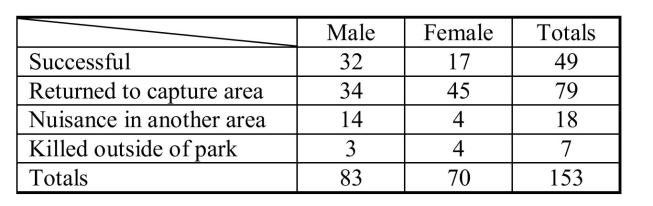 a) If a bear is randomly selected from the 153 bears in the sample, what is the
a) If a bear is randomly selected from the 153 bears in the sample, what is the
probability it is male and became a nuisance in another area after relocation?
b) If a bear is randomly selected from the 153 bears in the sample, what is the
probability that it is female or was successfully transplanted?
c) If a bear is randomly selected from the bears in the sample, what is the probability
that it returned to the capture area, given that it is a female?
d) After combining the above data with other National Parks, officials estimated that
only about 22% of black bears in all parks become enough of a nuisance to be
transplanted. They further estimate that 84% of nuisance bears are male, and fifty
percent of non-nuisance bears are females. If a randomly selected bear were
observed to be a male, what is the probability it would be enough of a nuisance to
be transplanted?
they have a high level of curiosity. These characteristics will sometimes get them
into trouble when they travel through national parks. When they become "nuisances,"
the Park Service transplants them to other areas if possible. Data on the gender of
transplanted bears and the outcome of the transplant for bears transplanted in Glacier
National Park over a 10-year period are given in the table below.
 a) If a bear is randomly selected from the 153 bears in the sample, what is the
a) If a bear is randomly selected from the 153 bears in the sample, what is theprobability it is male and became a nuisance in another area after relocation?
b) If a bear is randomly selected from the 153 bears in the sample, what is the
probability that it is female or was successfully transplanted?
c) If a bear is randomly selected from the bears in the sample, what is the probability
that it returned to the capture area, given that it is a female?
d) After combining the above data with other National Parks, officials estimated that
only about 22% of black bears in all parks become enough of a nuisance to be
transplanted. They further estimate that 84% of nuisance bears are male, and fifty
percent of non-nuisance bears are females. If a randomly selected bear were
observed to be a male, what is the probability it would be enough of a nuisance to
be transplanted?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
30
Forty-five percent of donors have type O blood. The blood bank needs 4 donors with
type O blood to restock their reserves. The director has the option of waiting to get 4
type O donors during the day, or ordering type O blood from a neighboring blood
bank. Your task is to design and conduct a simulation to estimate the probability it
takes 12 or more donors to get 4 with type O blood. c) Using the following lines from a random digit table, perform three runs of your
c) Using the following lines from a random digit table, perform three runs of your
simulation. Based on your results, what is your estimate of the probability of getting
4 Type O donors before 12 donors arrive at the blood bank? (You may mark above
the digits to help explain your procedure.)
type O blood to restock their reserves. The director has the option of waiting to get 4
type O donors during the day, or ordering type O blood from a neighboring blood
bank. Your task is to design and conduct a simulation to estimate the probability it
takes 12 or more donors to get 4 with type O blood.
 c) Using the following lines from a random digit table, perform three runs of your
c) Using the following lines from a random digit table, perform three runs of yoursimulation. Based on your results, what is your estimate of the probability of getting
4 Type O donors before 12 donors arrive at the blood bank? (You may mark above
the digits to help explain your procedure.)


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
31
A small ferryboat transports vehicles from one island to another. Consider the chance
experiment where the type of vehicle -- passenger (P) or recreational (R) vehicle -- is
recorded for each of the next two vehicles that arrive at the dock.
a) List all the outcomes in the sample space.
b) Using the sample space in part (a), list the outcomes in each of the following events.
experiment where the type of vehicle -- passenger (P) or recreational (R) vehicle -- is
recorded for each of the next two vehicles that arrive at the dock.
a) List all the outcomes in the sample space.
b) Using the sample space in part (a), list the outcomes in each of the following events.


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
32
In the survey of travelers described in problem 2, passengers were also classified by
age: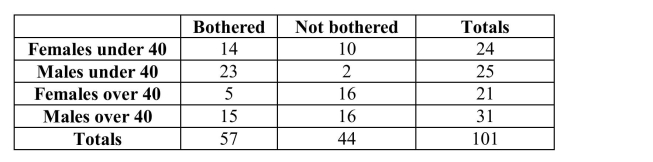 Suppose one of these passengers is to be randomly selected. Calculate the probability
Suppose one of these passengers is to be randomly selected. Calculate the probability
that:
a) The selected passenger is under 40, given that the passenger is female.
b) The selected passenger is bothered, given that the passenger is over 40.
c) The selected passenger is male and over 40.
age:
 Suppose one of these passengers is to be randomly selected. Calculate the probability
Suppose one of these passengers is to be randomly selected. Calculate the probabilitythat:
a) The selected passenger is under 40, given that the passenger is female.
b) The selected passenger is bothered, given that the passenger is over 40.
c) The selected passenger is male and over 40.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
33
In a few sentences, explain the difference between an event, A, and the complement of
event A.
event A.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
34
For a special report in the Cedar Rapids, IA, Gazette, reporters used a radar gun to
check the speeds of 1,239 drivers in two counties. They were shocked (!) to discover
that some drivers were driving at a speed greater than the posted limits. They
reported the following information in their story: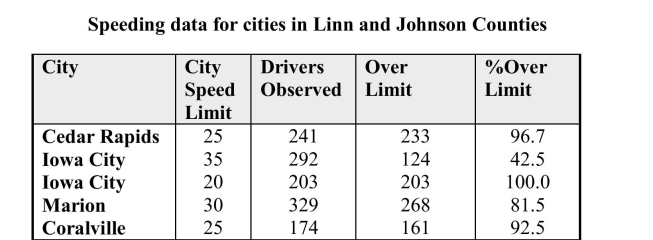 Suppose that one of these drivers is selected at random. Define the following events:
Suppose that one of these drivers is selected at random. Define the following events:
F = the event that a randomly selected driver was in the fast lane (speed limit
above 25 mph)
S = the event that a randomly selected driver is speeding.
a) The table below shows the possible combinations of F and S. For each
combination, calculate the probability that the combination would be observed for
a randomly selected driver. Enter these probabilities into the corresponding cell in
the table.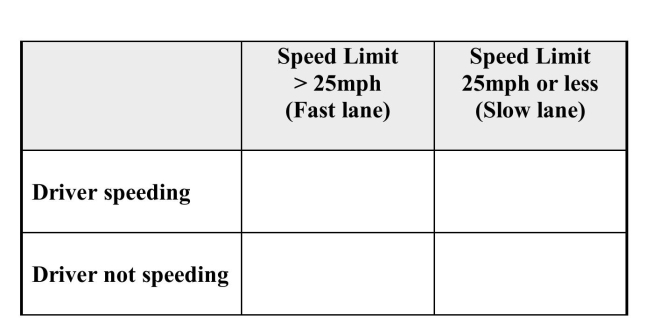

check the speeds of 1,239 drivers in two counties. They were shocked (!) to discover
that some drivers were driving at a speed greater than the posted limits. They
reported the following information in their story:
 Suppose that one of these drivers is selected at random. Define the following events:
Suppose that one of these drivers is selected at random. Define the following events:F = the event that a randomly selected driver was in the fast lane (speed limit
above 25 mph)
S = the event that a randomly selected driver is speeding.
a) The table below shows the possible combinations of F and S. For each
combination, calculate the probability that the combination would be observed for
a randomly selected driver. Enter these probabilities into the corresponding cell in
the table.

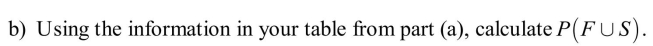


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
35
Understanding attitudes of humans towards wildlife is an important step in learning how to work with people on wildlife issues. Coyotes have expanded their range throughout the continental United States, even in the Washington, DC area. The data below are from a survey of George Mason University undergraduate students.
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.
What is the probability that the selected official is from Metro Athens?
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.What is the probability that the selected official is from Metro Athens?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
36
In a survey of airline travelers, passengers traveling alone in the coach section were
asked if they are bothered by a seatmate of the opposite gender using a shared
armrest.
The table below contains the data gathered in this study.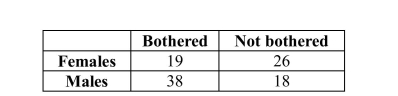 Suppose one of these passengers is to be randomly selected for a follow-up interview. Use the information in the table to answer the questions below. In showing your
Suppose one of these passengers is to be randomly selected for a follow-up interview. Use the information in the table to answer the questions below. In showing your
work, define and use appropriate notation.
a) What is the probability that the selected passenger is female?
b) What is the probability that the selected passenger is female or is bothered?
c) What is the probability that the selected passenger is male and is not bothered?
asked if they are bothered by a seatmate of the opposite gender using a shared
armrest.
The table below contains the data gathered in this study.
 Suppose one of these passengers is to be randomly selected for a follow-up interview. Use the information in the table to answer the questions below. In showing your
Suppose one of these passengers is to be randomly selected for a follow-up interview. Use the information in the table to answer the questions below. In showing yourwork, define and use appropriate notation.
a) What is the probability that the selected passenger is female?
b) What is the probability that the selected passenger is female or is bothered?
c) What is the probability that the selected passenger is male and is not bothered?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
37
First graders at an elementary school were classified according to whether they were
the first born child in the family or not, and also whether both parents worked outside
the home. This resulted in the accompanying table.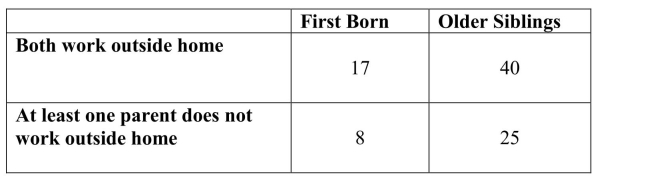 Suppose that one of these students is selected at random. Define events A, B, and C as
Suppose that one of these students is selected at random. Define events A, B, and C as
follows:
A = the event that the selected student is a first born
B = the event that the selected student's parents both work outside the home
C = the event that the selected student has older siblings
For each pair of events in the following table, indicate whether the two events are disjoint
and/or independent by putting a Y or N in the appropriate cells.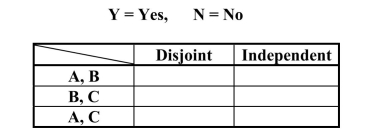
the first born child in the family or not, and also whether both parents worked outside
the home. This resulted in the accompanying table.
 Suppose that one of these students is selected at random. Define events A, B, and C as
Suppose that one of these students is selected at random. Define events A, B, and C asfollows:
A = the event that the selected student is a first born
B = the event that the selected student's parents both work outside the home
C = the event that the selected student has older siblings
For each pair of events in the following table, indicate whether the two events are disjoint
and/or independent by putting a Y or N in the appropriate cells.


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
38
Understanding attitudes of humans towards wildlife is an important step in learning how to work with people on wildlife issues. Coyotes have expanded their range throughout the continental United States, even in the Washington, DC area. The data below are from a survey of George Mason University undergraduate students.
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.
What is the probability that the selected student dislikes coyotes somewhat?
2. What is the probability that the selected student is male?
3. What is the probability that the selected student is male, given that he likes coyotes
very much?
4. What is the probability that the selected student dislikes coyotes very much, given
that she is a female?
 Suppose a newspaper decides to select one of these students at random for an interview.
Suppose a newspaper decides to select one of these students at random for an interview.What is the probability that the selected student dislikes coyotes somewhat?
2. What is the probability that the selected student is male?
3. What is the probability that the selected student is male, given that he likes coyotes
very much?
4. What is the probability that the selected student dislikes coyotes very much, given
that she is a female?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
39
Suppose 70% of orders on a particular website are shipped to the person who is
making the order and the remaining 30% are shipped to people other than the person
placing the order. Gift wrapping is requested for 60% of the orders being shipped to
other people, but for only 10% of orders shipped to the person making the order.
a) What is the probability that a randomly selected order will be gift wrapped and
sent to a person other than the person making the order?
b) What is the probability that a randomly selected order will be gift wrapped?
c) Is gift-wrapping independent of the destination of the gift? Provide a statistical
justification for your response.
making the order and the remaining 30% are shipped to people other than the person
placing the order. Gift wrapping is requested for 60% of the orders being shipped to
other people, but for only 10% of orders shipped to the person making the order.
a) What is the probability that a randomly selected order will be gift wrapped and
sent to a person other than the person making the order?
b) What is the probability that a randomly selected order will be gift wrapped?
c) Is gift-wrapping independent of the destination of the gift? Provide a statistical
justification for your response.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
40
At Thomas Jefferson High School, students are heavily involved in extra-curricular
activities. Suppose that a student is to be selected at random from the students at this
school. Let the events A, M, and S be defined as follows, with the probabilities
listed:
activities. Suppose that a student is to be selected at random from the students at this
school. Let the events A, M, and S be defined as follows, with the probabilities
listed:


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
41
In November 2002, Janet Napolitano, a Democrat, was elected Governor of Arizona,
defeating Republican Matt Salmon and Independent Richard Mahoney. This was a
somewhat surprising outcome, since there are more registered Republicans than
Democrats in the state. The table below presents data from a survey of a sample of
voters in the election. The candidate supported by the voter is represented by the
rows, and the party affiliation of the voter is represented by the columns. Suppose that one of these voters is selected at random. Use the information in the table to
a) What is the probability that the selected voter voted for Napolitano?
b) What is the probability that the selected voter is a registered Democrat?
c) What is the probability that the selected voter voted for Napolitano, given that the
selected voter is a Democrat?
d) A local reporter, commenting on this election, said, "Napolitano won because she
attracted a larger share of crossover voters." (A crossover voter is one who votes
differently than his or her registration category. For example, a Democrat party
member voting Republican, or an Independent voting for a Democrat candidate
would be crossover voters). What is the probability that the selected voter voted
for Napolitano, given that he or she is a crossover voter?
defeating Republican Matt Salmon and Independent Richard Mahoney. This was a
somewhat surprising outcome, since there are more registered Republicans than
Democrats in the state. The table below presents data from a survey of a sample of
voters in the election. The candidate supported by the voter is represented by the
rows, and the party affiliation of the voter is represented by the columns. Suppose that one of these voters is selected at random. Use the information in the table to
a) What is the probability that the selected voter voted for Napolitano?
b) What is the probability that the selected voter is a registered Democrat?
c) What is the probability that the selected voter voted for Napolitano, given that the
selected voter is a Democrat?
d) A local reporter, commenting on this election, said, "Napolitano won because she
attracted a larger share of crossover voters." (A crossover voter is one who votes
differently than his or her registration category. For example, a Democrat party
member voting Republican, or an Independent voting for a Democrat candidate
would be crossover voters). What is the probability that the selected voter voted
for Napolitano, given that he or she is a crossover voter?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
42
All statistics teachers love Girl Scout Cookies. The number of boxes of Girl Scout
cookies a statistics teacher orders is (of course) determined by the roll of a 4-sided
fair die. If a one appears, 6 boxes are ordered; if any other number appears, 2 boxes
are ordered.
a) What is the probability that a statistics teacher places an order for 2 boxes of Girl
Scout cookies?
b) What is the probability that two statistics teachers (each rolling a die to determine
the number of boxes ordered) will each order 6 boxes each?
c) What is the probability that for two statistics teachers (each rolling a die to
determine the number of boxes ordered), the first will order 6 boxes and the
second will order 2 boxes?
d) What is the probability that for two statistics teachers (each rolling a die to
determine the number of boxes ordered), exactly one will order 6 boxes?
cookies a statistics teacher orders is (of course) determined by the roll of a 4-sided
fair die. If a one appears, 6 boxes are ordered; if any other number appears, 2 boxes
are ordered.
a) What is the probability that a statistics teacher places an order for 2 boxes of Girl
Scout cookies?
b) What is the probability that two statistics teachers (each rolling a die to determine
the number of boxes ordered) will each order 6 boxes each?
c) What is the probability that for two statistics teachers (each rolling a die to
determine the number of boxes ordered), the first will order 6 boxes and the
second will order 2 boxes?
d) What is the probability that for two statistics teachers (each rolling a die to
determine the number of boxes ordered), exactly one will order 6 boxes?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
43
Three of the most common pets are cats, dogs, and fish. Many families have more
than one type of pet, and some have all three! Define the following events, with the
probabilities given. (The fish-and-cats combination doesn't seem too popular!)
than one type of pet, and some have all three! Define the following events, with the
probabilities given. (The fish-and-cats combination doesn't seem too popular!)


Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
44
The adult diamond python (Morelia spilota), an Australian snake, is about 3 feet long.
In a multi-year study of the habitats of these creatures, 997 were captured. The
following table displays the capture locations of these snakes by season of the year
and habitat. The "other" category includes trees, logs, rocks, open ground, and under
filtering cover such as shrubs.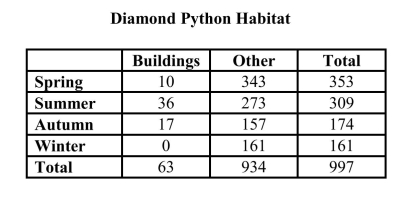 Suppose one of these diamond pythons is selected at random.
Suppose one of these diamond pythons is selected at random.
Calculate the probability that:
a) The selected diamond python was captured in a building, given that it was
captured in the spring.
b) The selected diamond python was captured somewhere other than in a building
given that it was captured in the spring or summer.
c) The selected diamond python was captured in a building in the summer.
In a multi-year study of the habitats of these creatures, 997 were captured. The
following table displays the capture locations of these snakes by season of the year
and habitat. The "other" category includes trees, logs, rocks, open ground, and under
filtering cover such as shrubs.
 Suppose one of these diamond pythons is selected at random.
Suppose one of these diamond pythons is selected at random.Calculate the probability that:
a) The selected diamond python was captured in a building, given that it was
captured in the spring.
b) The selected diamond python was captured somewhere other than in a building
given that it was captured in the spring or summer.
c) The selected diamond python was captured in a building in the summer.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
45
Like many professionals, the clergy in mainline Protestant churches have pension
plans. Due to the nature of the ministry, investment strategies may involve what are
known as "screens." Screens are rules that prevent a pension fund administrator from
investing in corporations that are involved with, for example, alcohol, gambling,
tobacco and weapons of mass destruction. Ministers may elect to invest in two broad
categories: "regular" and "social purpose" funds, which would typically use screens
in their investment strategy. The use of screens may reduce their monthly benefit at
retirement.
The data below are from a survey of ministers about their support in principle for the
use of such screens. Each minister asked if the screens should be applied to the
regular funds, the social purpose funds, both, or neither. The ministers were also
classified by the current percentage of their investments in the social purpose funds:
0%, 10 - 59%, 60% or greater.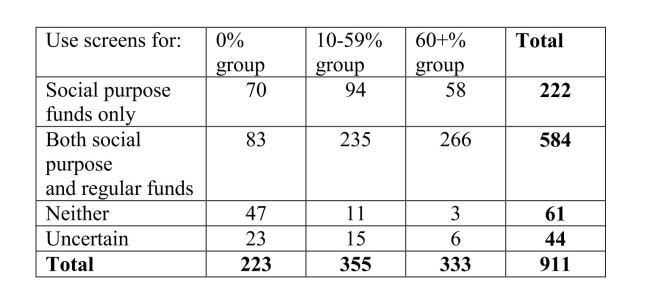 a) What is the probability that a minister selected at random from those who
a) What is the probability that a minister selected at random from those who
participated in the survey was uncertain about the use of screens?
b) What is the probability that a minister selected at random from those who
participated in the survey was in the 60+% group and supported the use of screens
for social purpose funds only?
c) What is the probability that a minister selected at random from those who
participated in the survey felt the screens should be used for social purpose funds
only or for both social purpose and regular funds, given that they were in the 10-
59% group?
d) What is the probability that a randomly selected "uncertain" minister would be in
the 0% group?
plans. Due to the nature of the ministry, investment strategies may involve what are
known as "screens." Screens are rules that prevent a pension fund administrator from
investing in corporations that are involved with, for example, alcohol, gambling,
tobacco and weapons of mass destruction. Ministers may elect to invest in two broad
categories: "regular" and "social purpose" funds, which would typically use screens
in their investment strategy. The use of screens may reduce their monthly benefit at
retirement.
The data below are from a survey of ministers about their support in principle for the
use of such screens. Each minister asked if the screens should be applied to the
regular funds, the social purpose funds, both, or neither. The ministers were also
classified by the current percentage of their investments in the social purpose funds:
0%, 10 - 59%, 60% or greater.
 a) What is the probability that a minister selected at random from those who
a) What is the probability that a minister selected at random from those whoparticipated in the survey was uncertain about the use of screens?
b) What is the probability that a minister selected at random from those who
participated in the survey was in the 60+% group and supported the use of screens
for social purpose funds only?
c) What is the probability that a minister selected at random from those who
participated in the survey felt the screens should be used for social purpose funds
only or for both social purpose and regular funds, given that they were in the 10-
59% group?
d) What is the probability that a randomly selected "uncertain" minister would be in
the 0% group?

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck


