Deck 7: Conic Sections
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/141
Play
Full screen (f)
Deck 7: Conic Sections
1
Suppose that the terminal point determined by t is the point on the unit circle. Find the terminal point determined by .
2
Find the sign of if the terminal point determined by t is in quadrant II.
negative
3
Find the exact value of and .
,
4
Find the period of the function and sketch its graph.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
5
Find the period of the function and sketch its graph.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
6
Find period and graph the function.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
7
Find the reference number and the terminal point determined by .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
8
The point is on the unit circle in quadrant IV. If find x.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
9
Find to two decimal places the approximate value of 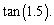

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
10
Use the fundamental identities to write the first expression in terms of the second. 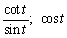

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
11
If the terminal point determined by t is , find , and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
12
Find the vertical asymptotes for the function in the interval .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
13
If and the terminal point for t is in quadrant IV, find .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
14
Find the reference number for 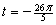
.
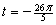
.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
15
Find given that and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
16
Find the amplitude, period and phase shift of 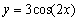
.
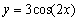
.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
17
Find the exact value of and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
18
Use a graphing device to find the maximum and minimum values of the function .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
19
Show that the point is on the unit circle.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
20
Find the amplitude, period, and phase shift of the function.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose that the terminal point determined by t is the point on the unit circle. Find the terminal point determined by .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
24
The point 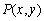
is on the unit circle in quadrant II. If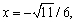
find y.
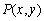
is on the unit circle in quadrant II. If
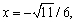
find y.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
25
The function models the displacement of an object moving in simple harmonic motion, where y is measured in inches and t in seconds. Find the amplitude, period, and frequency of motion and sketch a graph of the function over one complete period.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
26
Find the period of the function 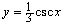
and sketch its graph.
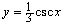
and sketch its graph.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
27
Show that the point is on the unit circle.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
28
If the terminal point determined by t is , find , and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
29
Find the exact value of the expression, if it is defined. 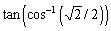
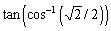

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
30
Find the exact value of 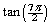
and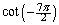
.
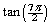
and
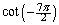
.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
31
Determine whether the function is even, odd, or neither. 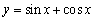
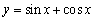

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
32
Find the reference number for 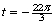
.
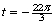
.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
33
Find a function that models simple harmonic motion having the given properties. Assume that the displacement is zero at time 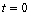
.amplitude 10 in, frequency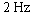
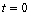
.amplitude 10 in, frequency
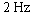

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
34
Find given that and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
35
If and the terminal point for t is in quadrant IV, find .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
36
Find to two decimal places the value of 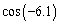
using a calculator.
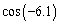
using a calculator.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
37
Find the reference number and the terminal point determined by .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
38
Express in terms of , if the terminal point determined by t is in quadrant III.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
39
Find the exact value of and .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
40
Find period and graph the function.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
41
Determine whether the function is even, odd, or neither. 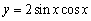
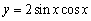

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
42
If the terminal point determined by t is , find , And
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
43
Find given that and
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose that the terminal point determined by t is the point on the unit circle. Find the terminal point determined by
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
45
If and the terminal point for t is in quadrant IV, find
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
46
Find the vertical asymptotes for the function in the interval .

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
47
Find the exact value of and
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
48
Find the exact value of each expression, if it is defined
a)
b) c)
a)
b) c)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
49
Find the reference number for
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
50
Find a function that models simple harmonic motion having the given properties. Assume that the displacement is maximum at time .amplitude , frequency

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
51
Find the exact value of and
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
53
Use a graphing device to find the maximum and minimum values of the function 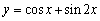
.
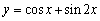
.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
54
Find the sign of and If the terminal point determined by tIs in quadrant II
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
55
The point 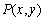 is on the unit circle in quadrant III. If
is on the unit circle in quadrant III. If 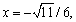
Find y
A)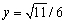
B)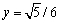
C)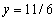
D)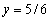
E)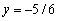
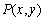 is on the unit circle in quadrant III. If
is on the unit circle in quadrant III. If 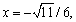
Find y
A)
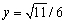
B)
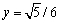
C)
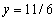
D)
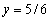
E)
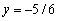

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
56
Find the amplitude, period, and phase shift of the function. 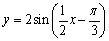

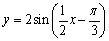


Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
57
Suppose that point is on the unit circle. Find and
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
58
Find to three decimal places the value of 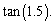
A)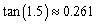
B)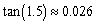
C)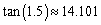
D)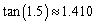
E) none
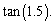
A)
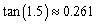
B)
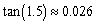
C)
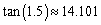
D)
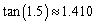
E) none

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
59
Use the fundamental identities to write the first expression in terms of the second.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
60
Find the reference number and the terminal point determined by
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
61
Find the period of the function
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
62
Suppose that point is on the unit circle. Find and
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
63
Graph the function. 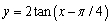
A)
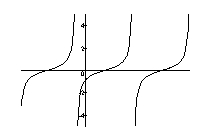



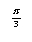
B)

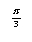
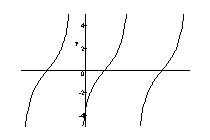
C)
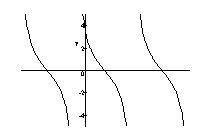

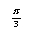
E) none
D)

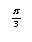
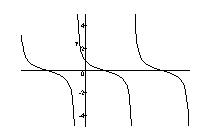

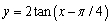
A)




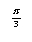
B)

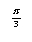

C)


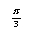
E) none
D)

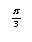



Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
64
Suppose that the terminal point determined by 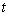 is the point
is the point 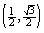
On the unit circle. Find the terminal point determined by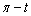
A)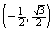
B)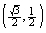
C)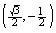
D)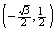
E)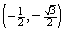
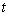 is the point
is the point 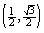
On the unit circle. Find the terminal point determined by
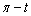
A)
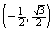
B)
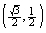
C)
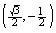
D)
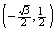
E)
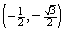

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
65
Find the exact value of 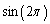 and
and 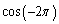
A)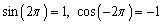
B)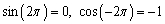
C)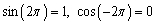
D)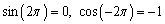
E) none of these
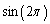 and
and 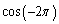
A)
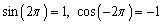
B)
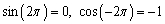
C)
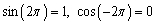
D)
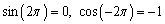
E) none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
66
Sketch the graph of the function.
A)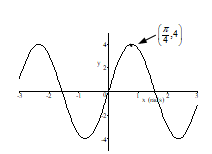
B)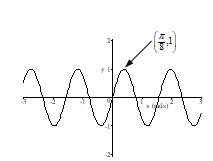
C)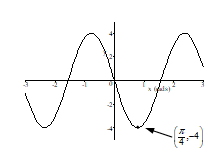
D)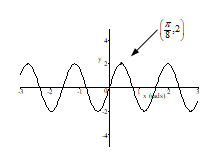
E) none
A)

B)

C)

D)

E) none

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
67
Use a graphing device to find the maximum and minimum values of the function
A)maximum value:
, minimum value:
B)maximum value:
, minimum value:
C)maximum value:
, minimum value:
D)maximum value:
, minimum value:
E) none of these
A)maximum value:
, minimum value:
B)maximum value:
, minimum value:
C)maximum value:
, minimum value:
D)maximum value:
, minimum value:
E) none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
68
Find the period of the function
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
69
Find the exact value of and
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
70
Find the approximate value of 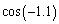 using a calculator
using a calculator
A)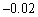
B)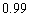
C)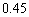
D)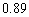
E)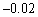
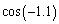 using a calculator
using a calculatorA)
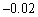
B)
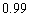
C)
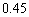
D)
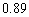
E)
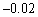

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
71
Use the fundamental identities to write the first expression in terms of the second.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
72
The function models the displacement of an object moving in simple harmonic motion, where y is measured in inches and t in seconds. Find frequency of motion
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
73
Find the reference number for
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
74
Determine whether the function is even, odd, or neither. 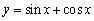
A)even
B)odd
C)neither
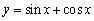
A)even
B)odd
C)neither

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
75
Find the reference number for
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
76
If the terminal point determined by is , find , And
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,
A) , ,
B) , ,
C) , ,
D) , ,
E) , ,

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
77
Find the vertical asymptotes for the function 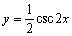 in the interval
in the interval 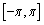
A)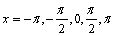
B)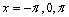
C)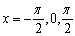
D)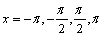
E)
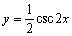 in the interval
in the interval 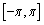
A)
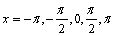
B)
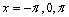
C)
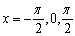
D)
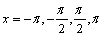
E)


Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
78
Find the exact value of the expression, if it is defined. 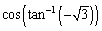
A)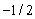
B)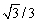
C)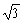
D)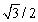
E)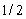
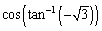
A)
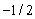
B)
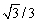
C)
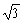
D)
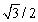
E)
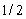

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
79
The point is on the unit circle in quadrant IV. If Find x
A)
B)
C)
D)
E)none of these
A)
B)
C)
D)
E)none of these

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
80
Find a function that models simple harmonic motion having the given properties. Assume that the displacement is zero at time 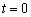 .amplitude 10 m, frequency
.amplitude 10 m, frequency 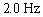
A)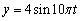
B)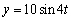
C)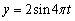
D)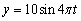
E)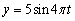
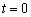 .amplitude 10 m, frequency
.amplitude 10 m, frequency 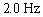
A)
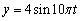
B)
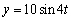
C)
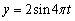
D)
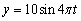
E)
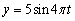

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
81
Determine whether the function is even, odd, or neither. 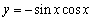
A)even
B)odd
C)neither
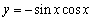
A)even
B)odd
C)neither

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
82
The point is on the unit circle in quadrant IV. If
find y.
find y.

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck
83
Which function has y-axis symmetry?
A)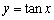
B)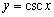
C)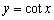
D)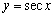
E) all have y-axis symmetry
A)
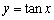
B)
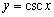
C)
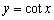
D)
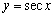
E) all have y-axis symmetry

Unlock Deck
Unlock for access to all 141 flashcards in this deck.
Unlock Deck
k this deck


