Deck 13: Sequences and Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/150
Play
Full screen (f)
Deck 13: Sequences and Series
1
Find the values of x and y for which the sequence 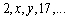
is arithmetic.
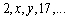
is arithmetic.
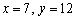
2
Dr. Stevens is considering a 30-year mortgage at 4% interest. She can make payments of $3500 a month. What size loan can she afford?
3
Find the amount of an annuity that consists of annual payments of each into an account that pays interest per year.
4
Find the fourth term and the term of the geometric sequence given
and
and

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
5
A man gets a job with a salary of $40,000 a year. He is promised an $1800 raise each subsequent year. Find his total earnings for a 10-year period.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
6
Write the sum without using sigma notation. Do not evaluate. 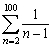
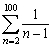

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether the expression is a partial sum of an arithmetic or geometric sequence. Then find the sum.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
8
A city was incorporated in 2004 with a population of 25,000. It is expected that the population will increase at a rate of 2% per year. The population n years after 2004 is given by the sequence 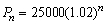
a) Find the first 5 terms of the sequence
b) Find the population in 2014.
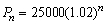
a) Find the first 5 terms of the sequence
b) Find the population in 2014.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
9
Given that the term of an arithmetic sequence is and the term is , find the first term.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
10
Find the first four terms and the term of the sequence

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
11
An arithmetic sequence has first term and common difference .
How many terms of this sequence must be added to get ?
How many terms of this sequence must be added to get ?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
12
The first four terms of a sequence are given. Determine whether they can be terms of an arithmetic sequence, a geometric sequence, or neither. If the sequence is arithmetic find the common difference. If the sequence is geometric find the common ratio. 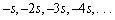
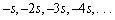

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
13
Find the first four terms and the term of the sequence

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
14
Determine whether the expression is a partial sum of a arithmetic or geometric sequence. Then find the sum. 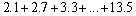
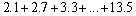

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
15
Find the 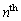
term of the sequence whose first several terms are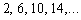
.
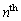
term of the sequence whose first several terms are
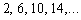
.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
16
Find the first five terms of the sequence 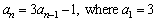
.
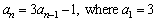
.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
17
How much money should be invested monthly at per year, compounded monthly, in order to have in two years?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
18
The common ratio of a geometric sequence is and the fourth term is
Find the third term.
Find the third term.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
19
Write the sum using sigma notation. 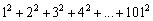
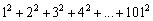

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
20
Which term of the arithmetic sequence is ?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
21
Find the first four terms and the term of the sequence

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
22
Determine whether the expression is a partial sum of an arithmetic or geometric sequence. Then find the sum.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
23
A city was incorporated in 2004 with a population of 45,000. It is expected that the population will increase at a rate of 2% per year. The population n years after 2004 is given by the sequence 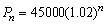
a) Find the first 5 terms of the sequence
b) Find the population in 2014.
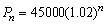
a) Find the first 5 terms of the sequence
b) Find the population in 2014.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
24
Express the repeating decimal
as a fraction.
as a fraction.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
25
Which term of the arithmetic sequence is ?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
26
Find the coefficient of in the expansion of

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
27
Find the term of the sequence whose first several terms are , , , ,.....

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
28
Write the sum using sigma notation. 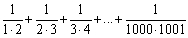
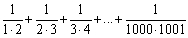

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
29
Find the first five terms of the sequence 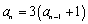
, where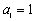
.
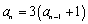
, where
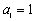
.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
30
Find the coefficient of in the expansion of

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
31
Find the fourth term and the term of the geometric sequence given and

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
32
Given that the term of an arithmetic sequence is and the common difference is , find the first three terms.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
33
Expand the expression 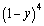
.
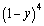
.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
34
The first term of a geometric sequence is and the second term is .
Find the fifth term.
Find the fifth term.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
35
The first four terms of a sequence are given. Determine whether they can be terms of an arithmetic sequence, a geometric sequence, or neither. If the sequence is arithmetic find the common difference. If the sequence is geometric find the common ratio. 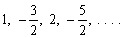

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
36
Write the sum without using sigma notation. Do not evaluate. 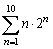
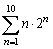

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
37
Find the sum of the infinite geometric series. 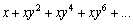
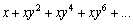

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
38
Find the second term in the expansion of 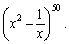
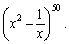

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
39
Find the first four terms and the term of the sequence

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
40
A man gets a job with a salary of $50,000 a year. He is promised an $1800 raise each subsequent year. Find his total earnings for a 10-year period.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
41
Dr. Stevens is considering a 30-year mortgage at 6% interest. She can make payments of $2500 a month. What size loan can she afford?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
42
Find the amount of an annuity that consists of 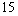
annual payments of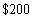
each into an account that pays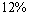
interest per year.
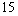
annual payments of
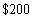
each into an account that pays
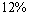
interest per year.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
43
How much money must be invested now at 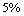
per year, compounded semi-annually, to fund an annuity of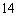
semi-annual payments of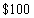
each, the first payment being six months after the initial investment?
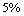
per year, compounded semi-annually, to fund an annuity of
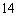
semi-annual payments of
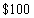
each, the first payment being six months after the initial investment?

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
44
The first four terms of a sequence are given. Determine whether they can be terms of an arithmetic sequence, a geometric sequence, or neither. If the sequence is arithmetic find the common difference. If the sequence is geometric find the common ratio.
A) arithmetic,
B) arithmetic,
C) geomettic,
D) geometric,
E) neither
A) arithmetic,
B) arithmetic,
C) geomettic,
D) geometric,
E) neither

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
45
Given that the term of an arithmetic sequence is and the common difference is , find the first three terms
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
46
Determine the common ratio, the fifth, and the terms of the geometric sequence.
A)
B)
C)
D)
E)none
A)
B)
C)
D)
E)none

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
47
Find the fourth term of the geometric sequence given 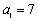 and
and 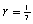
A)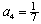
B)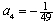
C)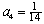
D)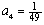
E)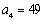
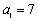 and
and 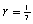
A)
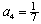
B)
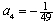
C)
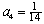
D)
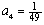
E)
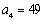

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
48
Find the first four terms of the sequence
A) , , ,
B) , , ,
C) , , ,
D) , , ,
E) , , ,
A) , , ,
B) , , ,
C) , , ,
D) , , ,
E) , , ,

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
49
A city was incorporated in 2004 with a population of 25,000. It is expected that the population will increase at a rate of 2% per year. The population n years after 2004 is given by the sequence 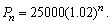 Find the population in 2014
Find the population in 2014
A)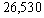
B)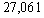
C)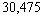
D)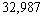
E) none of these
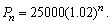 Find the population in 2014
Find the population in 2014A)
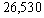
B)
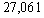
C)
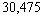
D)
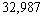
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
50
Find the sum of the infinite geometric series. 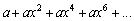
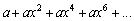

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
51
Express the repeating decimal as a fraction.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
52
Find the coefficient of in the expansion of

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
53
Expand the expression

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
54
The first term of the arithmetic sequence is and the common difference is Which term of this sequence is ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
55
Find the term of the sequence whose first several terms are
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
56
Determine whether the expression is a partial sum of an arithmetic or geometric sequence. Then find the sum.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
57
Find the term of the sequence
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
58
The seventh term of an arithmetic sequence is and the seventeenth term is .
Find the twenty-fourth term.
Find the twenty-fourth term.

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
59
Find the second term in the expansion of 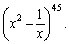
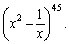

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
60
Find the first five terms of the sequence , where
A) , , , ,
B) , , , ,
C) , , , ,
D) , , , ,
E) none of these
A) , , , ,
B) , , , ,
C) , , , ,
D) , , , ,
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
61
Find the amount of an annuity that consists of 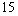 annual payments of
annual payments of 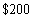
Each into an account that pays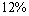
Interest per year
A)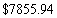
B)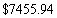
C)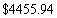
D)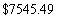
E)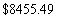
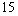 annual payments of
annual payments of 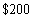
Each into an account that pays
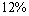
Interest per year
A)
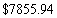
B)
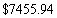
C)
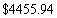
D)
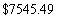
E)
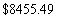

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
62
Write the sum without using sigma notation. 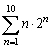
A)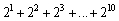
B)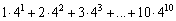
C)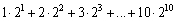
D)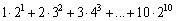
E) none of these
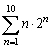
A)
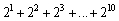
B)
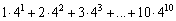
C)
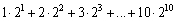
D)
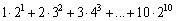
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
63
Find the first four terms sequence
A) , , ,
B) , , ,
C) , , ,
D) , , ,
E)none of these
A) , , ,
B) , , ,
C) , , ,
D) , , ,
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
64
Find the second term in the expansion of 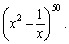
A)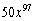
B)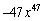
C)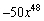
D)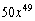
E)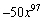
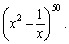
A)
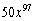
B)
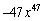
C)
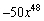
D)
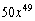
E)
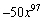

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
65
Dr. Stevens is considering a 30-year mortgage at 4% interest. She can make payments of $3500 a month. What size loan can she afford?
A)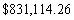
B)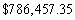
C)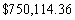
D)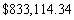
E)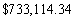
A)
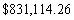
B)
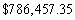
C)
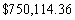
D)
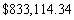
E)
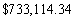

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
66
Determine whether the expression is a partial sum of an arithmetic or geometric sequence. Then find the sum.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
67
How much money must be invested now at 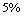 per year, compounded semi-annually, to fund an annuity of
per year, compounded semi-annually, to fund an annuity of 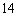
Semi-annual payments of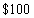
Each, the first payment being six months after the initial investment?
A)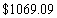
B)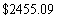
C)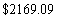
D)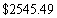
E)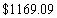
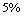 per year, compounded semi-annually, to fund an annuity of
per year, compounded semi-annually, to fund an annuity of 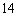
Semi-annual payments of
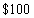
Each, the first payment being six months after the initial investment?
A)
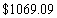
B)
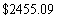
C)
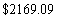
D)
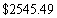
E)
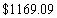

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
68
Find the first five terms of the sequence
A) , , , ,
B) , , , ,
C) , , , ,
D) , , , ,
E) none of these
A) , , , ,
B) , , , ,
C) , , , ,
D) , , , ,
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
69
Find the term of the sequence
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
70
Find the sum of the infinite geometric series. 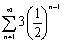
A)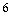
B)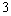
C)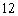
D)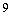
E)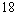
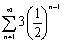
A)
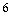
B)
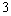
C)
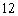
D)
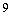
E)
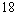

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
71
Find the 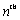 term of the sequence whose first several terms are
term of the sequence whose first several terms are 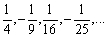
A)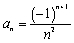
B)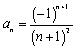
C)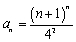
D)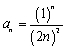
E) none of these
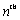 term of the sequence whose first several terms are
term of the sequence whose first several terms are 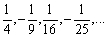
A)
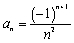
B)
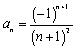
C)
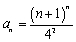
D)
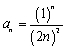
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
72
A man gets a job with a salary of $50,000 a year. He is promised an $1800 raise each subsequent year. Find his total earnings for a 10-year period
A)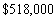
B)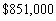
C)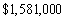
D)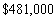
E)none of these
A)
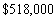
B)
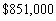
C)
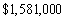
D)
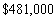
E)none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
73
Find the sum.
A)
B)
C)
D)
E) none of these
A)
B)
C)
D)
E) none of these

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
74
Write the sum using sigma notation.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
75
A ball rebounds to one-quarter the height from which it was dropped. Approximate the total vertical distance the ball travels after being dropped from 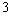 ft above the ground, until it comes to rest
ft above the ground, until it comes to rest
A)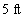
B)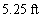
C)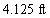
D)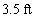
E)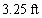
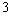 ft above the ground, until it comes to rest
ft above the ground, until it comes to restA)
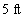
B)
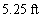
C)
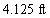
D)
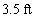
E)
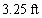

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
76
Find the coefficient of 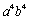 in the expansion of
in the expansion of 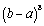
A)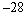
B)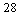
C)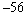
D)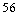
E)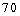
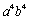 in the expansion of
in the expansion of 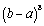
A)
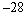
B)
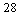
C)
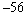
D)
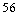
E)
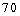

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
77
The first four terms of a sequence are given. Determine whether they can be terms of an arithmetic sequence, a geometric sequence, or neither. If the sequence is arithmetic find the common difference. If the sequence is geometric find the common ratio.
A)
B)
C)
D)
E) neither
A)
B)
C)
D)
E) neither

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
78
The seventh term of an arithmetic sequence is 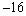 and the tenth term is
and the tenth term is 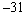
) Find the twenty-fourth term
A)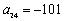
B)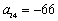
C)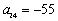
D)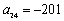
E)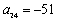
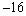 and the tenth term is
and the tenth term is 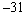
) Find the twenty-fourth term
A)
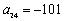
B)
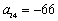
C)
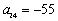
D)
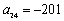
E)
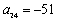

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
79
Expand the expression. 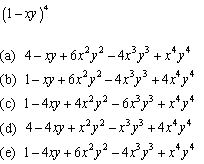
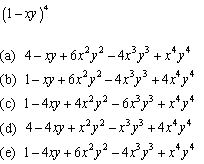

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck
80
Find the values of a and b for which the sequence 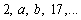 is arithmetic
is arithmetic
A)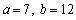
B)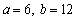
C)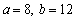
D)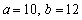
E)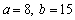
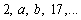 is arithmetic
is arithmeticA)
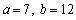
B)
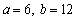
C)
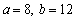
D)
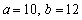
E)
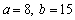

Unlock Deck
Unlock for access to all 150 flashcards in this deck.
Unlock Deck
k this deck


