Deck 10: Nonlinear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/38
Play
Full screen (f)
Deck 10: Nonlinear Programming
1
A well-known manufacturer of several brands of toothpaste uses the production lot size model to determine production quantities for its various products. The product known as Extra White is currently being produced in production lot sizes of 5000 units. The length of the production run for this quantity is 10 days. Because of a recent shortage of a particular raw material, the supplier of the material announced that a cost increase will be passed along to the manufacturer of Extra White. Current estimates are that the new raw material cost will increase the manufacturing cost of the toothpaste products by 23% per unit. What will be the effect of this price increase on the production lot sizes for Extra White?
Compute the effect of the price increase of 23% per unit on the production lot size of 5,000 units, by using the lot size Q formula 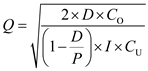 …… (1)Where D is the demand in the year, C O is the production set up cost, P is the the annual production rate, I is the annual holding rate and C U is the unit cost
…… (1)Where D is the demand in the year, C O is the production set up cost, P is the the annual production rate, I is the annual holding rate and C U is the unit cost
Other things being equal, from the above equation (1), the ratio of new production lot size Q N to the old production lot size Q O is as follows …… (2)Where C UO is the old unit cost and C UN is the new unit cost
…… (2)Where C UO is the old unit cost and C UN is the new unit cost
Substitute in equation (2), the value of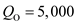 and
and 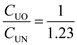 to obtain
to obtain 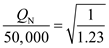 Rearrange and obtain
Rearrange and obtain  The new production lot size is 4,508 units.
The new production lot size is 4,508 units.
Given the production capacity of 500 units per day, the length of the production run for the new production lot size of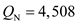 units would be
units would be 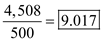 days.
days.
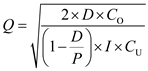 …… (1)Where D is the demand in the year, C O is the production set up cost, P is the the annual production rate, I is the annual holding rate and C U is the unit cost
…… (1)Where D is the demand in the year, C O is the production set up cost, P is the the annual production rate, I is the annual holding rate and C U is the unit costOther things being equal, from the above equation (1), the ratio of new production lot size Q N to the old production lot size Q O is as follows
 …… (2)Where C UO is the old unit cost and C UN is the new unit cost
…… (2)Where C UO is the old unit cost and C UN is the new unit costSubstitute in equation (2), the value of
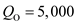 and
and 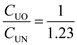 to obtain
to obtain 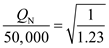 Rearrange and obtain
Rearrange and obtain  The new production lot size is 4,508 units.
The new production lot size is 4,508 units. Given the production capacity of 500 units per day, the length of the production run for the new production lot size of
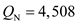 units would be
units would be 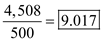 days.
days. 2
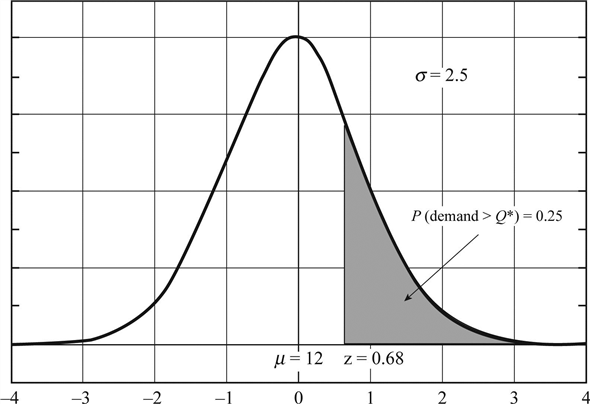
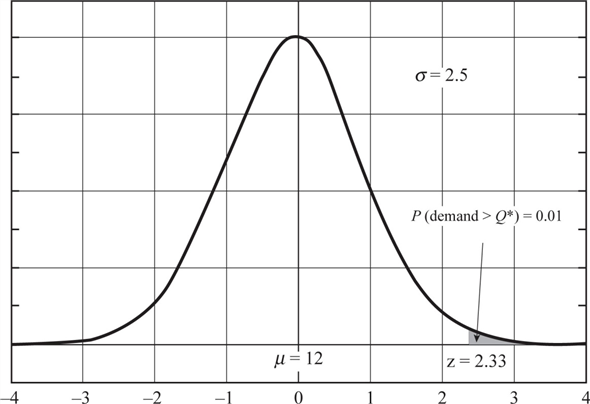
For Floyd Distributors in Problem 29, we were given Q * = 25, D = 200, C h , = $5, and a normal lead-time demand distribution with ? = 12 and ? = 2.5.
a. What is Floyd's reorder point if the firm is willing to tolerate two stockouts during the year?
b. What is Floyd's reorder point if the firm wants to restrict the probability of a stockout on any one cycle to at most 1 %?
c. What are the safety stock levels and the annual safety stock costs for the reorder points found in parts (a) and (b)?
a. What is Floyd's reorder point if the firm is willing to tolerate two stockouts during the year?
b. What is Floyd's reorder point if the firm wants to restrict the probability of a stockout on any one cycle to at most 1 %?
c. What are the safety stock levels and the annual safety stock costs for the reorder points found in parts (a) and (b)?
a)To calculate the revised reorder point, given the EOQ is 25 mufflers per order and the total annual demand is 200 mufflers, first derive the number of orders per year as 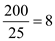 Since the management can tolerate two stockout per year, two out of the eight orders can be delivered late, which means that the probability of a stockout is
Since the management can tolerate two stockout per year, two out of the eight orders can be delivered late, which means that the probability of a stockout is 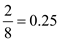 From the normal distribution table, find the z value as shown in the figure,
From the normal distribution table, find the z value as shown in the figure, 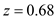 .
.  Calculate the revised reorder point r by using the formula
Calculate the revised reorder point r by using the formula 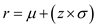 where the mean
where the mean 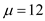 ,
, 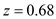 and the standard deviation
and the standard deviation 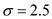 .
.
Substitute the values and obtain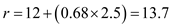 Rounding off, the revised reorder point is 14 mufflers , so that no more than two stockouts take place in a year.
Rounding off, the revised reorder point is 14 mufflers , so that no more than two stockouts take place in a year.
b)To derive the reorder point, to restrict the probability of a stockout to 1%, proceed as per the following steps.
From the normal distribution table find the z value as shown in the figure,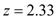 .
.  Calculate the revised reorder point r by using the formula
Calculate the revised reorder point r by using the formula 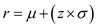 where the mean
where the mean 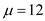 ,
, 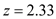 and the standard deviation
and the standard deviation 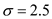 .
.
Substitute the values and obtain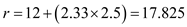 Rounding off, the revised reorder point is 18 mufflers , so that the probability of a stockout in one cycle is no more than 1%.
Rounding off, the revised reorder point is 18 mufflers , so that the probability of a stockout in one cycle is no more than 1%.
c)• The safety stock to ensure that the number of stockouts is limited to two per year , is the difference between the revised reorder point and the consumption of mufflers during the lead time or the original reorder point. Therefore, the safety stock ( S ) is 14 mufflers less 12 mufflers= 2 mufflers.
Given the holding cost is $5/unit/year, the additional cost of the safety stocks is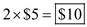 per year.
per year.
• The safety stock to ensure that the probability of a stockout in one cycle is no more than 1% in a cycle, is the difference between the revised reorder point and the consumption of mufflers during the lead time or the original reorder point.
Therefore, the safety stock ( S ) is 18 mufflers less 12 mufflers= 6 mufflers.
Given the holding cost is $5/unit/year, the additional cost of the safety stocks is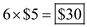 per year.
per year.
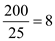 Since the management can tolerate two stockout per year, two out of the eight orders can be delivered late, which means that the probability of a stockout is
Since the management can tolerate two stockout per year, two out of the eight orders can be delivered late, which means that the probability of a stockout is 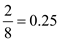 From the normal distribution table, find the z value as shown in the figure,
From the normal distribution table, find the z value as shown in the figure, 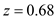 .
.  Calculate the revised reorder point r by using the formula
Calculate the revised reorder point r by using the formula 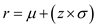 where the mean
where the mean 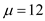 ,
, 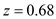 and the standard deviation
and the standard deviation 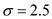 .
.Substitute the values and obtain
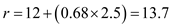 Rounding off, the revised reorder point is 14 mufflers , so that no more than two stockouts take place in a year.
Rounding off, the revised reorder point is 14 mufflers , so that no more than two stockouts take place in a year.b)To derive the reorder point, to restrict the probability of a stockout to 1%, proceed as per the following steps.
From the normal distribution table find the z value as shown in the figure,
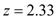 .
.  Calculate the revised reorder point r by using the formula
Calculate the revised reorder point r by using the formula 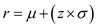 where the mean
where the mean 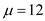 ,
, 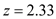 and the standard deviation
and the standard deviation 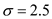 .
.Substitute the values and obtain
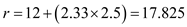 Rounding off, the revised reorder point is 18 mufflers , so that the probability of a stockout in one cycle is no more than 1%.
Rounding off, the revised reorder point is 18 mufflers , so that the probability of a stockout in one cycle is no more than 1%.c)• The safety stock to ensure that the number of stockouts is limited to two per year , is the difference between the revised reorder point and the consumption of mufflers during the lead time or the original reorder point. Therefore, the safety stock ( S ) is 14 mufflers less 12 mufflers= 2 mufflers.
Given the holding cost is $5/unit/year, the additional cost of the safety stocks is
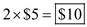 per year.
per year. • The safety stock to ensure that the probability of a stockout in one cycle is no more than 1% in a cycle, is the difference between the revised reorder point and the consumption of mufflers during the lead time or the original reorder point.
Therefore, the safety stock ( S ) is 18 mufflers less 12 mufflers= 6 mufflers.
Given the holding cost is $5/unit/year, the additional cost of the safety stocks is
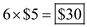 per year.
per year. 3
WAGNER FABRICATING COMPANY
Managers at Wagner Fabricating Company are reviewing the economic feasibility of manufacturing a part that it currently purchases from a supplier. Forecasted annual demand for the part is 3200 units. Wagner operates 250 days per year.
Wagner's financial analysts established a cost of capital of 14% for the use of funds for investments within the company. In addition, over the past year $600,000 was the average investment in the company's inventory. Accounting information shows that a total of $24,000 was spent on taxes and insurance related to the company's inventory. In addition, an estimated $9000 was lost due to inventory shrinkage, which included damaged goods as well as pilferage. A remaining $15,000 was spent on warehouse overhead, including utility expenses for healing and lighting.
An analysis of the purchasing operation shows that approximately two hours are required to process and coordinate an order for the part regardless of the quantity ordered. Purchasing salaries average $28 per hour, including employee benefits. In addition, a detailed analysis of 125 orders showed that $2375 was spent on telephone, paper, and postage directly related to the ordering process.
A one-week lead time is required to obtain the part from the supplier. An analysis of demand during the lead time shows it is approximately normally distributed with a mean of 64 units and a standard deviation of 10 units. Service level guidelines indicate that one stockout per year is acceptable.
Currently, the company has a contract to purchase the part from a supplier at a cost of $18 per unit. However, over the past few months, the company's production capacity has been expanded. As a result, excess capacity is now available in certain production departments, and the company is considering the alternative of producing the parts itself.
Forecasted utilization of equipment shows that production capacity will be available for the part being considered. The production capacity is available at the rate of 1000 units per month, with up to live months of production time available. Management believes that with a two-week lead time, schedules can be arranged so that the part can be produced whenever needed. The demand during the two-week lead time is approximately normally distributed, with a mean of 128 units and a standard deviation of 20 units. Production costs are expected to be $17 per part.
A concern of management is that setup costs will be significant. The total cost of labor and lost production time is estimated to be $50 per hour, and a full eight-hour shift will be needed to set up the equipment for producing the part.
Managerial Report
Develop a report for management of Wagner Fabricating that will address the question of whether the company should continue to purchase the part from the supplier or begin to produce the part itself. Include the following factors in your report:
1. An analysis of the holding costs, including the appropriate annual holding cost rate
2. An analysis of ordering costs, including the appropriate cost per order from the supplier
3. An analysis of setup costs for the production operation
4. A development of the inventory policy for the following two alternatives:
a. Ordering a fixed quantity Q from the supplier
b. Ordering a fixed quantity Q from in-plant production
5. Include the following in the policies of parts 4(a) and 4(b):
a. Optimal quantity Q *
b. Number of order or production runs per year
c. Cycle time
d. Reorder point
e. Amount of safety stock
f. Expected maximum inventory
g. Average inventory
h. Annual bolding cost
i. Annual ordering cost
j. Annual cost of the units purchased or manufactured
k. Total annual cost of the purchase policy and the total annual cost of the production policy
6. Make a recommendation as to whether the company should purchase or manufacture the part What savings are associated with your recommendation as compared with the other alternative?
Managers at Wagner Fabricating Company are reviewing the economic feasibility of manufacturing a part that it currently purchases from a supplier. Forecasted annual demand for the part is 3200 units. Wagner operates 250 days per year.
Wagner's financial analysts established a cost of capital of 14% for the use of funds for investments within the company. In addition, over the past year $600,000 was the average investment in the company's inventory. Accounting information shows that a total of $24,000 was spent on taxes and insurance related to the company's inventory. In addition, an estimated $9000 was lost due to inventory shrinkage, which included damaged goods as well as pilferage. A remaining $15,000 was spent on warehouse overhead, including utility expenses for healing and lighting.
An analysis of the purchasing operation shows that approximately two hours are required to process and coordinate an order for the part regardless of the quantity ordered. Purchasing salaries average $28 per hour, including employee benefits. In addition, a detailed analysis of 125 orders showed that $2375 was spent on telephone, paper, and postage directly related to the ordering process.
A one-week lead time is required to obtain the part from the supplier. An analysis of demand during the lead time shows it is approximately normally distributed with a mean of 64 units and a standard deviation of 10 units. Service level guidelines indicate that one stockout per year is acceptable.
Currently, the company has a contract to purchase the part from a supplier at a cost of $18 per unit. However, over the past few months, the company's production capacity has been expanded. As a result, excess capacity is now available in certain production departments, and the company is considering the alternative of producing the parts itself.
Forecasted utilization of equipment shows that production capacity will be available for the part being considered. The production capacity is available at the rate of 1000 units per month, with up to live months of production time available. Management believes that with a two-week lead time, schedules can be arranged so that the part can be produced whenever needed. The demand during the two-week lead time is approximately normally distributed, with a mean of 128 units and a standard deviation of 20 units. Production costs are expected to be $17 per part.
A concern of management is that setup costs will be significant. The total cost of labor and lost production time is estimated to be $50 per hour, and a full eight-hour shift will be needed to set up the equipment for producing the part.
Managerial Report
Develop a report for management of Wagner Fabricating that will address the question of whether the company should continue to purchase the part from the supplier or begin to produce the part itself. Include the following factors in your report:
1. An analysis of the holding costs, including the appropriate annual holding cost rate
2. An analysis of ordering costs, including the appropriate cost per order from the supplier
3. An analysis of setup costs for the production operation
4. A development of the inventory policy for the following two alternatives:
a. Ordering a fixed quantity Q from the supplier
b. Ordering a fixed quantity Q from in-plant production
5. Include the following in the policies of parts 4(a) and 4(b):
a. Optimal quantity Q *
b. Number of order or production runs per year
c. Cycle time
d. Reorder point
e. Amount of safety stock
f. Expected maximum inventory
g. Average inventory
h. Annual bolding cost
i. Annual ordering cost
j. Annual cost of the units purchased or manufactured
k. Total annual cost of the purchase policy and the total annual cost of the production policy
6. Make a recommendation as to whether the company should purchase or manufacture the part What savings are associated with your recommendation as compared with the other alternative?
1.
Calculate the annual inventory holding costs given the various components as
• Cost of capital @ 14% of investment in the inventory i.e. 0.14
• Taxes and insurance ($24,000 for an inventory of $600,000)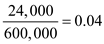 • Inventory shrinkage losses ($9,000 for an inventory of $600,000)
• Inventory shrinkage losses ($9,000 for an inventory of $600,000) 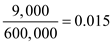 • Warehouse overhead such as utility expenses ($15,000 for inventory of $600,000)
• Warehouse overhead such as utility expenses ($15,000 for inventory of $600,000) 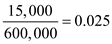 Therefore total inventory holding cost is
Therefore total inventory holding cost is 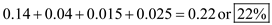 The inventory holding cost rate is 22% per year.
The inventory holding cost rate is 22% per year.
2.
Compute the ordering costs per order, given the various components as
• Two hours of purchasing operation given salary costs @ $28 per hour thus, $56(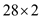 ) for two hours.
) for two hours.
• Additional order processing costs, given that the expenditure was $2,375 for 125 orders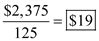 Therefore, the total costs per order is
Therefore, the total costs per order is 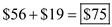 3.
3.
Calculate the production setup costs, given that the cost of labour and lost production time is $50 per hour. Further, given that eight hour shift is required to set up the equipment, the total setup cost is per setup.
per setup.
4.a)Develop a least cost inventory policy model, when the part is outsourced as follows.
a. Derive the Economic Order Quantity, given the demand for the part per year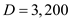 parts, the cost of ordering
parts, the cost of ordering  per order, the holding costs are at 22% and the unit purchase cost ( C ) of the part is $18 by using the formula
per order, the holding costs are at 22% and the unit purchase cost ( C ) of the part is $18 by using the formula 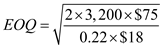 …… (1)Substitute in equation (1), the values of
…… (1)Substitute in equation (1), the values of 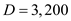 parts,
parts,  per order,
per order, 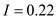 and
and 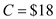 per case to obtain
per case to obtain 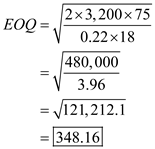 The economic order quantity is 348.16 parts.
The economic order quantity is 348.16 parts.
b. Calculate the number of orders per year ( N ), given that the demand for the part per year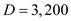 parts and the economic order quantity
parts and the economic order quantity 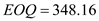 parts per order as shown
parts per order as shown 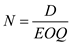 Substitute the values of
Substitute the values of 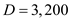 parts and the economic order quantity
parts and the economic order quantity 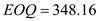 parts to obtain the number of orders per year ( N )
parts to obtain the number of orders per year ( N ) 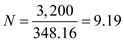 units
units
The number of orders placed per year is 9.19 units.
c. Calculate the cycle time ( T ) given that the company operates 250 days in a year and the number of orders placed per year is 9.19 as shown.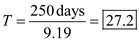 days
days
The cycle time is 27.2 days.
d.
Calculate the reorder point given that the average demand during lead time is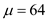 parts, the standard deviation is
parts, the standard deviation is 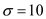 parts and one stockout per year is allowed as per the company policy, by first calculating "the probability of demand being greater than the quantity available" as follows.
parts and one stockout per year is allowed as per the company policy, by first calculating "the probability of demand being greater than the quantity available" as follows.
Out of 9.19 orders placed per year, the stockout allowed is one cycle per year.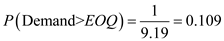 Use the normal distribution tables to arrive at the z value
Use the normal distribution tables to arrive at the z value 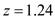 as shown in figure.
as shown in figure. 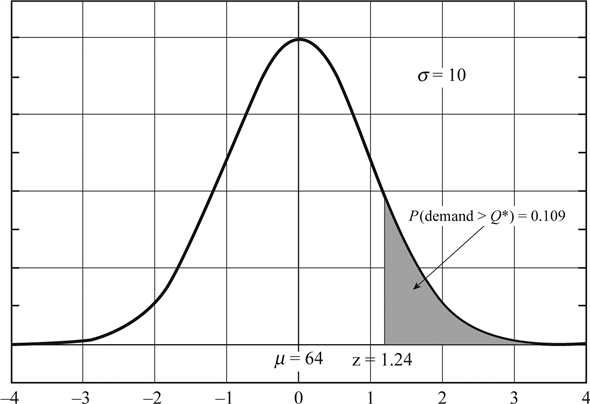 Calculate the reorder point r , by using the formula
Calculate the reorder point r , by using the formula 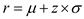 where the mean
where the mean 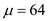 ,
, 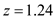 and the standard deviation
and the standard deviation 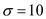 .
.
Substitute the values and obtain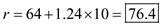 The reorder point is 76.4 parts.
The reorder point is 76.4 parts.
e. Derive the safety stock level ( S ) given the mean demand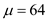 and the reorder level
and the reorder level 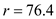 parts, by using the formula
parts, by using the formula 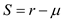 .
.
Substitute the values of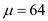 and
and 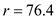 parts, to obtain S.
parts, to obtain S. 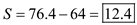 parts.
parts.
The safety stock is 12.4 parts.
f. Calculate the expected maximum inventory , given that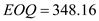 parts and the safety stock level
parts and the safety stock level 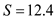 parts as follows.
parts as follows.
The maximum inventory level is reached when the ordered quantity is delivered. There is already the safety stock level of inventory when the ordered quantity is delivered. Therefore, the maximum inventory is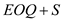 Substitute the values and obtain the expected maximum inventory
Substitute the values and obtain the expected maximum inventory 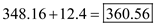 parts.
parts.
g. In each cycle, the inventory level declines from the maximum level of 360.56 parts to the safety stock level of 12.4 parts, just before the ordered quantity is delivered. Therefore, the average inventory is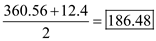 parts
parts
h. Calculate the annual holding costs, given the average inventory is 186.48 parts and the holdings costs are reckoned at 22%, where the unit purchase cost is $18 per part as follows.
Annual holding costs are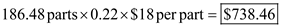 i. Compute the total ordering costs per year, given that the number of orders per year is 9.19 and the cost per order is $75 as follows.
i. Compute the total ordering costs per year, given that the number of orders per year is 9.19 and the cost per order is $75 as follows.
Total ordering costs per year is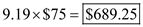 j. Compute the cost of purchasing the part from the supplier, given that the annual requirements are
j. Compute the cost of purchasing the part from the supplier, given that the annual requirements are 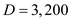 parts and the purchase price is $18 per part as
parts and the purchase price is $18 per part as 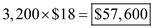 .
.
k. The total annual costs of outsourcing the parts is the purchase cost of 3,200 parts per year @$18 per part plus the annual holding costs of $738.46 plus the total ordering costs per year of $689.25.
Therefore, the total annual costs of outsourcing the parts is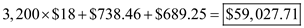 b)
b)
Develop a least cost inventory policy model, when the part is manufactured in-house as follows.
a. Compute the minimum cost production lot size Q , given that the demand during the year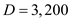 parts per year, the production setup cost is
parts per year, the production setup cost is 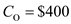 per setup, the holding cost is at 22% per year and the unit cost of one part is $17 and the production rate per year
per setup, the holding cost is at 22% per year and the unit cost of one part is $17 and the production rate per year 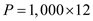 copies, by using the formula
copies, by using the formula 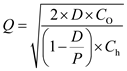 …… (2)Substitute in equation (2), the values of
…… (2)Substitute in equation (2), the values of 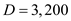 parts per year, the production rate per year
parts per year, the production rate per year 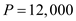 parts per year,
parts per year, 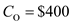 per setup and
per setup and 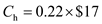 per year to obtain
per year to obtain  The minimum cost production lot size is 966.12 parts.
The minimum cost production lot size is 966.12 parts.
b. Calculate the number of production runs , given the demand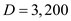 parts per year and the minimum cost production lot size is
parts per year and the minimum cost production lot size is 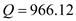 parts by using the formula
parts by using the formula
Number of production runs in a year is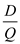 Substitute the values of
Substitute the values of 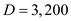 parts per year and
parts per year and 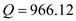 parts, to obtain the number of production runs in a year
parts, to obtain the number of production runs in a year 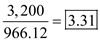 c. Compute the cycle time , given the number of production days in a year is 250 working days and the number of production runs is 3.31 as shown
c. Compute the cycle time , given the number of production days in a year is 250 working days and the number of production runs is 3.31 as shown  The cycle time is 75.53 days.
The cycle time is 75.53 days.
d. To calculate the reorder point , first calculate the probability of a stockout or the probability of the demand being greater than the parts availability, given that the company can accept one stockout cycle in a year, out of the 3.31 cycle runs in a year.
Probability of demand being greater than the parts availability is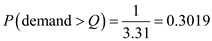 Use the normal distribution tables for deriving the z value
Use the normal distribution tables for deriving the z value 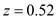 as shown in figure.
as shown in figure. 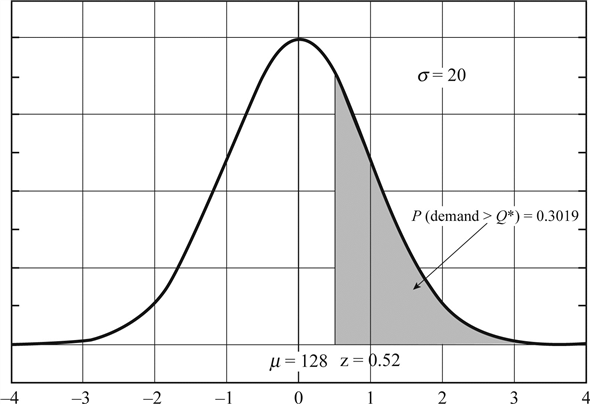 Calculate the reorder point by using the formula
Calculate the reorder point by using the formula 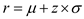 where the mean
where the mean 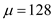 ,
, 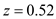 and the standard deviation
and the standard deviation 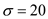 .
.
Substitute the values and obtain the reorder point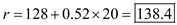 e.
e.
Calculate the safety stock level , given that the mean demand during the two week lead time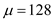 and the reorder point
and the reorder point 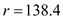 parts,as follows:
parts,as follows:
The safety stock is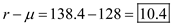 parts.
parts.
f. Derive the expected maximum inventor y, given the demand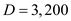 parts, the production capacity
parts, the production capacity 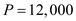 parts per year, the minimum cost production lot is
parts per year, the minimum cost production lot is 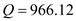 parts and the safety stock level
parts and the safety stock level 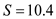 parts, by using the formula.
parts, by using the formula.
Maximum inventory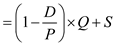 Substitute the values of
Substitute the values of 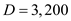 ,
, 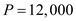 ,
, 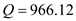 and
and 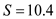 , to obtain the maximum inventory
, to obtain the maximum inventory 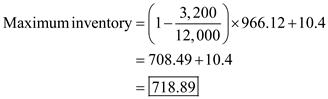 The expected maximum inventory 718.89 parts.
The expected maximum inventory 718.89 parts.
g. Calculate the average inventory , given that the expected maximum inventory is 718.89 parts and the expected minimum inventory is the safety stock of 10.4 parts during each cycle.
Therefore, the average inventory is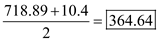 parts.
parts.
h. Compute the annual holding cost, given the average inventory during the year is 364.64 parts, the annual rate of holding is 22% and the unit cost is $17 as follows.
The annual holding cost is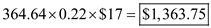 i. Derive the annual setup costs , given that there are 3.31 production runs in a year and the setup costs per production run is $400 as follows.
i. Derive the annual setup costs , given that there are 3.31 production runs in a year and the setup costs per production run is $400 as follows.
The annual setup cost is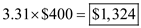 j. Compute the cost of manufacturing in-house , given that the annual requirements are
j. Compute the cost of manufacturing in-house , given that the annual requirements are 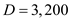 parts and the manufacturing cost is $17 per part as
parts and the manufacturing cost is $17 per part as 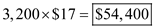 .
.
k. The total annual cost of manufacturing the parts is the production cost of 3,200 parts @ $17 per part plus the annual holding costs plus the annual setup costs.
Therefore, the total annual cost of manufacturing the parts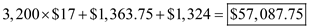 6.
6.
Compare the total cost of outsourcing, which is higher at $59,027.71 as against the total cost of in house production which is at $57,087.75.
The total cost of inhouse production is cheaper by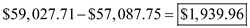 Therefore, recommend for in-house production of the part.
Therefore, recommend for in-house production of the part.
Calculate the annual inventory holding costs given the various components as
• Cost of capital @ 14% of investment in the inventory i.e. 0.14
• Taxes and insurance ($24,000 for an inventory of $600,000)
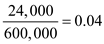 • Inventory shrinkage losses ($9,000 for an inventory of $600,000)
• Inventory shrinkage losses ($9,000 for an inventory of $600,000) 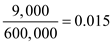 • Warehouse overhead such as utility expenses ($15,000 for inventory of $600,000)
• Warehouse overhead such as utility expenses ($15,000 for inventory of $600,000) 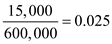 Therefore total inventory holding cost is
Therefore total inventory holding cost is 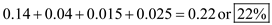 The inventory holding cost rate is 22% per year.
The inventory holding cost rate is 22% per year.2.
Compute the ordering costs per order, given the various components as
• Two hours of purchasing operation given salary costs @ $28 per hour thus, $56(
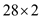 ) for two hours.
) for two hours. • Additional order processing costs, given that the expenditure was $2,375 for 125 orders
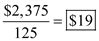 Therefore, the total costs per order is
Therefore, the total costs per order is 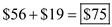 3.
3.Calculate the production setup costs, given that the cost of labour and lost production time is $50 per hour. Further, given that eight hour shift is required to set up the equipment, the total setup cost is
 per setup.
per setup.4.a)Develop a least cost inventory policy model, when the part is outsourced as follows.
a. Derive the Economic Order Quantity, given the demand for the part per year
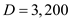 parts, the cost of ordering
parts, the cost of ordering  per order, the holding costs are at 22% and the unit purchase cost ( C ) of the part is $18 by using the formula
per order, the holding costs are at 22% and the unit purchase cost ( C ) of the part is $18 by using the formula 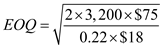 …… (1)Substitute in equation (1), the values of
…… (1)Substitute in equation (1), the values of 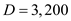 parts,
parts,  per order,
per order, 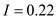 and
and 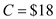 per case to obtain
per case to obtain 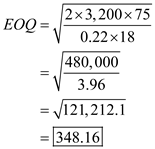 The economic order quantity is 348.16 parts.
The economic order quantity is 348.16 parts. b. Calculate the number of orders per year ( N ), given that the demand for the part per year
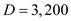 parts and the economic order quantity
parts and the economic order quantity 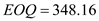 parts per order as shown
parts per order as shown 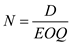 Substitute the values of
Substitute the values of 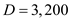 parts and the economic order quantity
parts and the economic order quantity 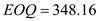 parts to obtain the number of orders per year ( N )
parts to obtain the number of orders per year ( N ) 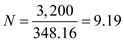 units
unitsThe number of orders placed per year is 9.19 units.
c. Calculate the cycle time ( T ) given that the company operates 250 days in a year and the number of orders placed per year is 9.19 as shown.
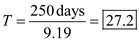 days
daysThe cycle time is 27.2 days.
d.
Calculate the reorder point given that the average demand during lead time is
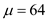 parts, the standard deviation is
parts, the standard deviation is 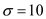 parts and one stockout per year is allowed as per the company policy, by first calculating "the probability of demand being greater than the quantity available" as follows.
parts and one stockout per year is allowed as per the company policy, by first calculating "the probability of demand being greater than the quantity available" as follows. Out of 9.19 orders placed per year, the stockout allowed is one cycle per year.
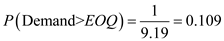 Use the normal distribution tables to arrive at the z value
Use the normal distribution tables to arrive at the z value 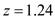 as shown in figure.
as shown in figure.  Calculate the reorder point r , by using the formula
Calculate the reorder point r , by using the formula 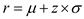 where the mean
where the mean 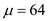 ,
, 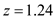 and the standard deviation
and the standard deviation 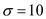 .
.Substitute the values and obtain
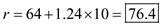 The reorder point is 76.4 parts.
The reorder point is 76.4 parts. e. Derive the safety stock level ( S ) given the mean demand
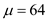 and the reorder level
and the reorder level 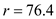 parts, by using the formula
parts, by using the formula 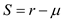 .
.Substitute the values of
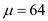 and
and 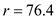 parts, to obtain S.
parts, to obtain S. 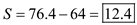 parts.
parts.The safety stock is 12.4 parts.
f. Calculate the expected maximum inventory , given that
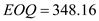 parts and the safety stock level
parts and the safety stock level 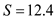 parts as follows.
parts as follows.The maximum inventory level is reached when the ordered quantity is delivered. There is already the safety stock level of inventory when the ordered quantity is delivered. Therefore, the maximum inventory is
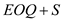 Substitute the values and obtain the expected maximum inventory
Substitute the values and obtain the expected maximum inventory 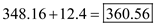 parts.
parts.g. In each cycle, the inventory level declines from the maximum level of 360.56 parts to the safety stock level of 12.4 parts, just before the ordered quantity is delivered. Therefore, the average inventory is
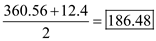 parts
partsh. Calculate the annual holding costs, given the average inventory is 186.48 parts and the holdings costs are reckoned at 22%, where the unit purchase cost is $18 per part as follows.
Annual holding costs are
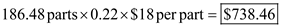 i. Compute the total ordering costs per year, given that the number of orders per year is 9.19 and the cost per order is $75 as follows.
i. Compute the total ordering costs per year, given that the number of orders per year is 9.19 and the cost per order is $75 as follows.Total ordering costs per year is
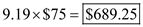 j. Compute the cost of purchasing the part from the supplier, given that the annual requirements are
j. Compute the cost of purchasing the part from the supplier, given that the annual requirements are 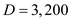 parts and the purchase price is $18 per part as
parts and the purchase price is $18 per part as 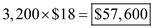 .
.k. The total annual costs of outsourcing the parts is the purchase cost of 3,200 parts per year @$18 per part plus the annual holding costs of $738.46 plus the total ordering costs per year of $689.25.
Therefore, the total annual costs of outsourcing the parts is
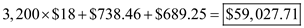 b)
b) Develop a least cost inventory policy model, when the part is manufactured in-house as follows.
a. Compute the minimum cost production lot size Q , given that the demand during the year
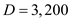 parts per year, the production setup cost is
parts per year, the production setup cost is 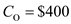 per setup, the holding cost is at 22% per year and the unit cost of one part is $17 and the production rate per year
per setup, the holding cost is at 22% per year and the unit cost of one part is $17 and the production rate per year 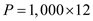 copies, by using the formula
copies, by using the formula 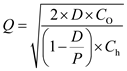 …… (2)Substitute in equation (2), the values of
…… (2)Substitute in equation (2), the values of 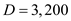 parts per year, the production rate per year
parts per year, the production rate per year 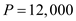 parts per year,
parts per year, 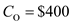 per setup and
per setup and 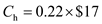 per year to obtain
per year to obtain  The minimum cost production lot size is 966.12 parts.
The minimum cost production lot size is 966.12 parts. b. Calculate the number of production runs , given the demand
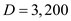 parts per year and the minimum cost production lot size is
parts per year and the minimum cost production lot size is 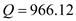 parts by using the formula
parts by using the formulaNumber of production runs in a year is
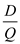 Substitute the values of
Substitute the values of 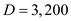 parts per year and
parts per year and 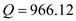 parts, to obtain the number of production runs in a year
parts, to obtain the number of production runs in a year 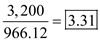 c. Compute the cycle time , given the number of production days in a year is 250 working days and the number of production runs is 3.31 as shown
c. Compute the cycle time , given the number of production days in a year is 250 working days and the number of production runs is 3.31 as shown  The cycle time is 75.53 days.
The cycle time is 75.53 days.d. To calculate the reorder point , first calculate the probability of a stockout or the probability of the demand being greater than the parts availability, given that the company can accept one stockout cycle in a year, out of the 3.31 cycle runs in a year.
Probability of demand being greater than the parts availability is
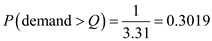 Use the normal distribution tables for deriving the z value
Use the normal distribution tables for deriving the z value 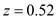 as shown in figure.
as shown in figure.  Calculate the reorder point by using the formula
Calculate the reorder point by using the formula 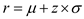 where the mean
where the mean 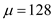 ,
, 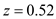 and the standard deviation
and the standard deviation 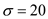 .
.Substitute the values and obtain the reorder point
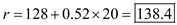 e.
e. Calculate the safety stock level , given that the mean demand during the two week lead time
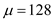 and the reorder point
and the reorder point 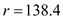 parts,as follows:
parts,as follows: The safety stock is
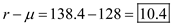 parts.
parts.f. Derive the expected maximum inventor y, given the demand
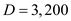 parts, the production capacity
parts, the production capacity 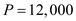 parts per year, the minimum cost production lot is
parts per year, the minimum cost production lot is 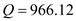 parts and the safety stock level
parts and the safety stock level 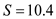 parts, by using the formula.
parts, by using the formula.Maximum inventory
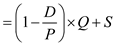 Substitute the values of
Substitute the values of 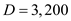 ,
, 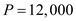 ,
, 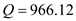 and
and 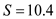 , to obtain the maximum inventory
, to obtain the maximum inventory 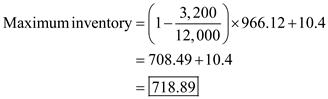 The expected maximum inventory 718.89 parts.
The expected maximum inventory 718.89 parts. g. Calculate the average inventory , given that the expected maximum inventory is 718.89 parts and the expected minimum inventory is the safety stock of 10.4 parts during each cycle.
Therefore, the average inventory is
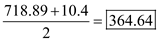 parts.
parts.h. Compute the annual holding cost, given the average inventory during the year is 364.64 parts, the annual rate of holding is 22% and the unit cost is $17 as follows.
The annual holding cost is
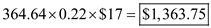 i. Derive the annual setup costs , given that there are 3.31 production runs in a year and the setup costs per production run is $400 as follows.
i. Derive the annual setup costs , given that there are 3.31 production runs in a year and the setup costs per production run is $400 as follows.The annual setup cost is
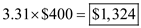 j. Compute the cost of manufacturing in-house , given that the annual requirements are
j. Compute the cost of manufacturing in-house , given that the annual requirements are 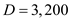 parts and the manufacturing cost is $17 per part as
parts and the manufacturing cost is $17 per part as 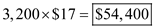 .
.k. The total annual cost of manufacturing the parts is the production cost of 3,200 parts @ $17 per part plus the annual holding costs plus the annual setup costs.
Therefore, the total annual cost of manufacturing the parts
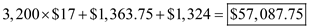 6.
6.Compare the total cost of outsourcing, which is higher at $59,027.71 as against the total cost of in house production which is at $57,087.75.
The total cost of inhouse production is cheaper by
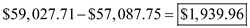 Therefore, recommend for in-house production of the part.
Therefore, recommend for in-house production of the part. 4
Suppose that Westside Auto of Problem 4, with D = 12,000 units per year. C h = (2.50)(0.20) = $0.50, and C o = $25, decided to operate with a backorder inventory policy. Backorder costs are estimated to be $5 per unit per year. Identify the following:
a. Minimum cost order quantity
b. Maximum number of backorders
c. Maximum inventory
d. Cycle time
e. Total annual cost
a. Minimum cost order quantity
b. Maximum number of backorders
c. Maximum inventory
d. Cycle time
e. Total annual cost

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
5
A product with an annual demand of 1000 units has C O = $25.50 and C h = $8, The demand exhibits some variability such that the lead-time demand follows a normal probability distribution with ? = 25 and ? = 5.
a. What is the recommended order quantity?
b. What are the reorder point and safety stock if the firm desires at most a 2% probability of stockout on any given order cycle?
c. If a manager sets the reorder point at 30, what is the probability of a stockout on any given order cycle? How many times would you expect a stockout during the year if this reorder point were used?
a. What is the recommended order quantity?
b. What are the reorder point and safety stock if the firm desires at most a 2% probability of stockout on any given order cycle?
c. If a manager sets the reorder point at 30, what is the probability of a stockout on any given order cycle? How many times would you expect a stockout during the year if this reorder point were used?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose that the R B Beverage Company has a soft drink product that shows a constant annual demand rate of 3600 cases. A case of the soft drink costs R B $3. Ordering costs are $20 per order and holding costs are 25% of the value of the inventory. R B has 250 working days per year, and the lead time is 5 days. Identify the following aspects of the inventory policy:
a. Economic order quantity
b. Reorder point
c. Cycle time
d. Total annual cost
a. Economic order quantity
b. Reorder point
c. Cycle time
d. Total annual cost

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
7
Assuming 250 days of operation per year and a lead time of 5 days, what is the reorder point for Westside Auto in Problem 15? Show the general formula for the reorder point for the EOQ model with backorders. In general, is the reorder point when backorder are allowed greater than or less than the reorder point when backorders are not allowed? Explain.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
8
The B S Novelty and Craft Shop in Bennington, Vermont, sells a variety of quality handmade items to tourists. B S will sell 300 hand-carved miniature replicas of a Colonial soldier each year, but the demand pattern during the year is uncertain. The replicas sell for $20 each, and B S uses a 15% annual inventory holding cost rate. Ordering costs are $5 per order, and demand during the lead time follows a normal probability distribution with ? = 15 and ? = 6.
a. What is the recommended order quantity?
b. If B S is willing to accept a stockout roughly twice a year, what reorder point would you recommend? What is the probability that B S will have a stockout in any one order cycle?
c. What are the safety stock and annual safety stock costs for this product?
a. What is the recommended order quantity?
b. If B S is willing to accept a stockout roughly twice a year, what reorder point would you recommend? What is the probability that B S will have a stockout in any one order cycle?
c. What are the safety stock and annual safety stock costs for this product?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
9
RIVER CITY FIRE DEPARTMENT
The River City Fire Department (RCPD) fights fires and provides a variety of rescue operations in the River City metropolitan area. The RCFD staffs 13 ladder companies, 26 pumper companies, and several rescue units and ambulances. Normal staffing requires 186 firefighters to be on duty every day.
RCFD is organized with three firefighting units. Each unit works a full 24-hour day and then has two days (48 hours) off. For example, Unit 1 covers Monday, Unit 2 covers Tuesday, and Unit 3 covers Wednesday. Then Unit 1 returns on Thursday, and so on. Over a three-week (21-day) scheduling period, each unit will be scheduled for seven days. On a rotational basis, firefighters within each unit are given one of the seven regularly scheduled days off. This day off is referred to as a Kelley day. Thus, over a three-week scheduling period, each firefighter in a unit works six of the seven scheduled unit days and gets one Kelley day off.
Determining the number of firefighters to be assigned to each unit includes the 186 firefighters who must be on duty plus the number of firefighters in the unit who are off for a Kelly day. Futhermore, each unit needs additional staffing to cover firefighter absences due to injury, sick leave, vacations, or personal time. This additional staffing involves finding the nest mix of adding full-time firefighters to each unit and the selective use of overtime. If the number of absences on a particular day brings the number of available firefighters below the required 186, firefighters who are currently off (e.g. on a Kelley day) must be scheduled to work overtime. Overtime is compensated at 1.55 times the regular pay rate.
Analysis of the records maintained over the last several years concerning the number of daily absences shows a normal probability distribution. A mean of 20 and a standard deviation of 5 provide a good approximation of the probability distribution for the number of daily absences.
Managerial Report
Develop a report that will enable Fire Chief O.E. Smith to determine the necessary numbers for the Fire Department. Include, at a minimum, the following items in your report:
1. Assuming no daily absences and taking into account the need to staff Kelley days, determine the base number of firefighters needed by each unit.
2. Using a minimum cost criterion, how many additional firefighters should be added to each unit in order to cover the daily absences? These extra daily needs will be filled by the additional firefighters and, when necessary, the more expensive use of overtime by off-duty firefighters.
3. On a given day, what is the probability that Kelley-day firefighters will be called in to work overtime?
4. Based on the three-unit organization, how many firefighters should be assigned to each unit? What is the total number of full-time firefighters required for the River City Fire Department?
The River City Fire Department (RCPD) fights fires and provides a variety of rescue operations in the River City metropolitan area. The RCFD staffs 13 ladder companies, 26 pumper companies, and several rescue units and ambulances. Normal staffing requires 186 firefighters to be on duty every day.
RCFD is organized with three firefighting units. Each unit works a full 24-hour day and then has two days (48 hours) off. For example, Unit 1 covers Monday, Unit 2 covers Tuesday, and Unit 3 covers Wednesday. Then Unit 1 returns on Thursday, and so on. Over a three-week (21-day) scheduling period, each unit will be scheduled for seven days. On a rotational basis, firefighters within each unit are given one of the seven regularly scheduled days off. This day off is referred to as a Kelley day. Thus, over a three-week scheduling period, each firefighter in a unit works six of the seven scheduled unit days and gets one Kelley day off.
Determining the number of firefighters to be assigned to each unit includes the 186 firefighters who must be on duty plus the number of firefighters in the unit who are off for a Kelly day. Futhermore, each unit needs additional staffing to cover firefighter absences due to injury, sick leave, vacations, or personal time. This additional staffing involves finding the nest mix of adding full-time firefighters to each unit and the selective use of overtime. If the number of absences on a particular day brings the number of available firefighters below the required 186, firefighters who are currently off (e.g. on a Kelley day) must be scheduled to work overtime. Overtime is compensated at 1.55 times the regular pay rate.
Analysis of the records maintained over the last several years concerning the number of daily absences shows a normal probability distribution. A mean of 20 and a standard deviation of 5 provide a good approximation of the probability distribution for the number of daily absences.
Managerial Report
Develop a report that will enable Fire Chief O.E. Smith to determine the necessary numbers for the Fire Department. Include, at a minimum, the following items in your report:
1. Assuming no daily absences and taking into account the need to staff Kelley days, determine the base number of firefighters needed by each unit.
2. Using a minimum cost criterion, how many additional firefighters should be added to each unit in order to cover the daily absences? These extra daily needs will be filled by the additional firefighters and, when necessary, the more expensive use of overtime by off-duty firefighters.
3. On a given day, what is the probability that Kelley-day firefighters will be called in to work overtime?
4. Based on the three-unit organization, how many firefighters should be assigned to each unit? What is the total number of full-time firefighters required for the River City Fire Department?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
10
A manager of an inventory system believes that inventory models are important decision-making aids. Even though often using an EOQ policy, the manager never considered a backorder model because of the assumption that backorders were "bad" and should be avoided. However, with upper management's continued pressure for cost reduction, you have been asked to analyze the economics of the backorder policy for some products that can possibly be backordered. For a specific product with D = 800 units per year, C O = $150, C h = $3, and C b = $20, what is the difference in total annual cost between the EOQ model and the planned shortage or backorder model? If the manager adds constraints that no more than 25% of the units can be backordered and that no customer will have to wait more than 15 days for an order, should the backorder inventory policy be adopted? Assume 250 working days per year.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
11
A firm uses a one-week periodic review inventory system. A two-day lead time is needed for any order, and the firm is willing to tolerate an average of one stockout per year.
a. Using the firm's service guideline, what is the probability of a stockout associated with each replenishment decision?
b. What is the replenishment level if demand during the review period plus lead-time period is normally distributed with a mean of 60 units and a standard deviation of 12 units?
c. What is the replenishment level if demand during the review period plus lead-time period is uniformly distributed between 35 and 85 units?
a. Using the firm's service guideline, what is the probability of a stockout associated with each replenishment decision?
b. What is the replenishment level if demand during the review period plus lead-time period is normally distributed with a mean of 60 units and a standard deviation of 12 units?
c. What is the replenishment level if demand during the review period plus lead-time period is uniformly distributed between 35 and 85 units?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
12
A general property of the EOQ inventory model is that total inventory holding and total ordering costs are equal at the optimal solution. Use the data in Problem 1 to show that this result is true. Use equations (10.2), (10.3), and (10.5) to show that, in general, total holding costs and total ordering costs are equal whenever Q * is used.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
13
If the lead time for new orders is 20 days for the inventory system discussed in Problem 17, find the reorder point for both the EOQ and the backorder models.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
14
Foster Drugs, Inc., handles a variety of health and beauty aid product. A particular hair conditioner product costs Hosier Drugs $2.95 per unit. The annual holding cost 20%. An order-quantity, reorder point inventory model recommends an order quantity 300 units per order.
a. Lead time is one week and the lead-time demand is normally distributed with a mean or 150 units and a standard deviation of 40 units. What is the reorder points if the firm is willing to tolerate a 1% chance stockout on any one cycle?
b. What safety stock and annual safety stock costs are associated with your recommendation in part (a)?
c. The order-quantity, reorder point model require a continuous review system. Management is considering making a transition to a periodic review system in an attempt to coordinate ordering for many of its products. The demand during the proposed two-week review period and the one-week lead-lime period is normally distributed with a mean of 450 units and a standard deviation of 70 units. What is the recommended replenishment level for this periodic review system if the firm is willing to tolerate the same 1% chance of stockout associated will, any replenishment decision?
d. What safety stock and annual safety costs are associated with your recommendation in part (c)?
e. Compare your answer to parts (b) and (d). The company is seriously considering the periodic review system. Would you support this decision? Explain.
f. Would you tend to favor the continuous in the preceding example sold for $295 per unit. Explain
a. Lead time is one week and the lead-time demand is normally distributed with a mean or 150 units and a standard deviation of 40 units. What is the reorder points if the firm is willing to tolerate a 1% chance stockout on any one cycle?
b. What safety stock and annual safety stock costs are associated with your recommendation in part (a)?
c. The order-quantity, reorder point model require a continuous review system. Management is considering making a transition to a periodic review system in an attempt to coordinate ordering for many of its products. The demand during the proposed two-week review period and the one-week lead-lime period is normally distributed with a mean of 450 units and a standard deviation of 70 units. What is the recommended replenishment level for this periodic review system if the firm is willing to tolerate the same 1% chance of stockout associated will, any replenishment decision?
d. What safety stock and annual safety costs are associated with your recommendation in part (c)?
e. Compare your answer to parts (b) and (d). The company is seriously considering the periodic review system. Would you support this decision? Explain.
f. Would you tend to favor the continuous in the preceding example sold for $295 per unit. Explain

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
15
The reorder point [see equation (10.6)1 is defined as the lead-time demand for an item. In cases ol long lead times, the lead-time demand and thus the reorder point may exceed the economic order quantity Q *. In such cases, the inventory position will not equal the inventory on hand when an order is placed, and the reorder point may be expressed in terms of either the inventory position or the inventory on hand. Consider the economic order quantity model with D = 5000, C o = $32, C h = $2, and 250 working days per year. Identify the reorder point in terms of the inventory position and in terms of the inventory on hand for each of the following lead times:
a. 5 clays
b. 15 days
c. 25 days
d. 45 days
a. 5 clays
b. 15 days
c. 25 days
d. 45 days

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
16
The A M Hobby Shop carries a line of radio-controlled model racing cars. Demand for the cars is assumed to be constant at a rate of 40 cars per month. The cars cost $60 each, and ordering costs are approximately $15 per order, regardless of the order size. The annual holding cost rate is 20%.
a. Determine the economic order quantity and total annual cost under the assumption that no backorders are permitted.
b. Using a $45 per-unit per-year backorder cost, determine the minimum cost inventory policy and total annual cost for the model racing cars.
c. What is the maximum number of days a customer would have to wait for a backorder under the policy in part (b)? Assume that the Hobby Shop is open for business 300 days per year.
d. Would you recommend a no-backorder or a backorder inventory policy for this product? Explain.
e. If the lead time is six days, what is the reorder point for both the no-backorder and backorder inventory policies?
a. Determine the economic order quantity and total annual cost under the assumption that no backorders are permitted.
b. Using a $45 per-unit per-year backorder cost, determine the minimum cost inventory policy and total annual cost for the model racing cars.
c. What is the maximum number of days a customer would have to wait for a backorder under the policy in part (b)? Assume that the Hobby Shop is open for business 300 days per year.
d. Would you recommend a no-backorder or a backorder inventory policy for this product? Explain.
e. If the lead time is six days, what is the reorder point for both the no-backorder and backorder inventory policies?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
17
Statewide Auto Parts uses a four-week periodic review system to reorder parts for its inventory stock. A one-week lead-time is required to fill the order. Demand for one particular part during the five-week replenishment period is normally distributed with a mean of 18 units and a standard deviation of 6 units.
a. At a particular review, 8 units are in inventory. The parts manager places an order for 16 units. What is the probability that this part will have a stockout before an order that is placed at the next four-week review period arrives?
b. Assume that the company is willing to tolerate a 2.5% chance of a stockout associated with a replenishment decision. How parts should he manager have ordered in part(a)? What is the replenishment level for the four-week periodic review system?
a. At a particular review, 8 units are in inventory. The parts manager places an order for 16 units. What is the probability that this part will have a stockout before an order that is placed at the next four-week review period arrives?
b. Assume that the company is willing to tolerate a 2.5% chance of a stockout associated with a replenishment decision. How parts should he manager have ordered in part(a)? What is the replenishment level for the four-week periodic review system?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
18
Westside Auto purchases a component used in the manufacture of automobile generators directly from the supplier. Westside's generator production operation, which is operated at a constant rate, will require 1000 components per month throughout the year (12,000 units annually). Assume that the ordering costs are $25 per order, the unit cost is $2.50 per component, and annual holding costs are 20% of the value of the inventory. Westside has 250 working days per year and a lead time of 5 days. Answer the following inventory policy
a. What is the EOQ for this component?
b. What is the reorder point?
c. What is the cycle time?
d. What are the total annual holding and ordering costs associated with your recommended EOQ
a. What is the EOQ for this component?
b. What is the reorder point?
c. What is the cycle time?
d. What are the total annual holding and ordering costs associated with your recommended EOQ

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
19
Assume that the following quantity discount schedule is appropriate. If annual demand is 120 units, ordering costs are $20 per order, and the annual holding cost rate is 25%, what order quantity would you recommend? 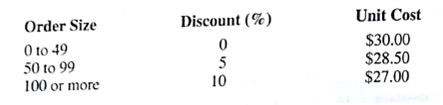
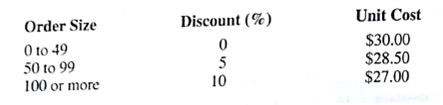

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
20
Rose Office Supplies, Inc., which is open six days a week, uses a two-week periodic review for its store inventory. On alternating Monday, mornings, the store manager fills out an order sheet requiring a shipment of various items from the company's warehouse. A particular three-ring notebook sells at an average rate of 16 notebooks per week. The standard deviation in sales is 5 notebooks per week. The lead time for a new shipment is three days. The mean lead-time demand is 8 notebooks with a standard deviation of 3.5.
a. What is the mean or expected demand during the review period plus the lead-time period?
b. Under the assumption of independent demand from week to week, the variances in demands are additive. Thus, the variance of the demand during the review period plus the lead-time period is equal to the variance of demand during the first week plus the variance of demand during the second week plus the variance of demand during the lead-time period. What is the variance of demand during the review period plus the lead-time period? What is the standard deviation of demand during the review period plus the lead-time period?
c. Assuming that demand has a normal probability distribution, what is the replenishment level that will provide an expected stockout rate of one per year?
d. On Monday, March 22, 18 notebooks remain in inventory at the store. How many notebooks should the store manager order?
a. What is the mean or expected demand during the review period plus the lead-time period?
b. Under the assumption of independent demand from week to week, the variances in demands are additive. Thus, the variance of the demand during the review period plus the lead-time period is equal to the variance of demand during the first week plus the variance of demand during the second week plus the variance of demand during the lead-time period. What is the variance of demand during the review period plus the lead-time period? What is the standard deviation of demand during the review period plus the lead-time period?
c. Assuming that demand has a normal probability distribution, what is the replenishment level that will provide an expected stockout rate of one per year?
d. On Monday, March 22, 18 notebooks remain in inventory at the store. How many notebooks should the store manager order?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose that Westside's management in Problem 4 likes the operational efficiency of ordering once each month and in quantities of 1000 units. How much more expensive would this policy be than your EOQ recommendation? Would you recommend in favour of the 1000-unit order quantity? Explain. What would the reorder point be if the 1000-unit quantity were acceptable?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
22
Apply the EOQ model to the following quantity discount situation in which D = 500 units per year, C O = $40, and the annual holding cost rate is 20%. What order quantity do you recommend? 


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
23
Tele-Reco is a new specialty store that sells television sets, videotape recorders, videogames, and other television-related products. A new Japanese-manufactured videotape recorder costs Tele-Reco $600 per unit. Tele-Reco's annual holding cost rate is 22%. Ordering costs are estimated to be $70 per order.
a. If demand for the new videotape recorder is expected to be constant with a rate of 20 units per month, what is the recommended order quantity for the videotape reorder?
b. What are the estimated annual inventory holding and ordering costs associated with this product?
c. How many orders will be placed per year?
d. With 250 working days per year, what is the cycle time for this product?
a. If demand for the new videotape recorder is expected to be constant with a rate of 20 units per month, what is the recommended order quantity for the videotape reorder?
b. What are the estimated annual inventory holding and ordering costs associated with this product?
c. How many orders will be placed per year?
d. With 250 working days per year, what is the cycle time for this product?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
24
Keith Shoe Stores carries a basic black men's dress shoe that sells at an approximate constant rate of 500 pairs of shoes every three months. Keith's current buying policy is to order 500 pairs each time an order is placed. It costs Keith $30 to place an order. The annual holding cost rate is 20%. With the order quantity of 500, Keith obtains the shoes at the lowest possible unit cost of $28 per pair. Other quantity discounts offered by the manufacturer are as follows. What is the minimum cost order quantity for the shoes? What are the annual savings of your inventory policy over the policy currently being used by Keith? 


Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
25
A large distributor of oil-well drilling equipment operated over the past two years with EOQ policies based on an annual holding cost rate of 22%. Under the EOQ policy, a particular product has been ordered with a Q * = 80. A recent evaluation of holding costs shows that because of an increase in the interest rate associated with bank loans, the annual holding cost rate should be 27%.
a. What is the new economic order quantity for the product?
b. Develop a general expression showing how the economic order quantity changes which the annual holding cost rate is changed from I to I ?.
a. What is the new economic order quantity for the product?
b. Develop a general expression showing how the economic order quantity changes which the annual holding cost rate is changed from I to I ?.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
26
In the EOQ model with quantity discounts, we stated that if the Q * for a price category is larger than necessary to qualify for the category price, the category cannot be optimal. Use the two discount categories in Problem 21 to show that this statement is true. That is, plot total cost curves for the two categories and show that if the category 2 minimum cost Q is an acceptable solution, we do not have to consider category 1.

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
27
Nation-Wide Bus Lines is proud of its six-week bus driver training program that it conducts for all new Nation-wide drivers. As long as the class size remains less than or equal to 35, a six-week training program costs Nation-Wide $22,000 for instructors, equipment, and so on. The Nation-Wide training program must provide the company with approximately five new drivers per month. After completing the training program, new drivers are paid $1600 per month but do not work until a full-time driver position is open. Nation-Wide views the $1600 per month paid to each idle new driver as a holding cost necessary to maintain a supply of newly trained drivers available for immediate service. Viewing new drivers as inventory-type units, how large should the training and new driver idle-time costs? How many training classes should the company hold each year? What is the total annual cost associated with your recommendation?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
28
The J B Card Shop sells calendars depicting a different Colonial scene each month. The once-a-year order for each year's calendar arrives in September. From past experience, the September-to-July demand for the calendars can be approximated by a normal probability distribution with ? = 500 and ? = 120. The calendars cost $1.50 each, and J B sells them for $3 each.
a. If J B throws out all unsold calendars at the end of July (i.e., salvage value is zero), how many calendars should be ordered?
b. If J B reduces the calendar price to $1 at the end of July and can sell a surplus calendars at this price, how many calendars should be ordered?
a. If J B throws out all unsold calendars at the end of July (i.e., salvage value is zero), how many calendars should be ordered?
b. If J B reduces the calendar price to $1 at the end of July and can sell a surplus calendars at this price, how many calendars should be ordered?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
29
Cress Electronic Products manufactures components used in the automotive industry. Cress purchases parts for use in its manufacturing operation from a variety of different suppliers. One particular supplier provides a part where the assumptions of the EOQ model are realistic. The annual demand is 5000 units, the ordering cost is $80 per order, and the annual holding cost rate is 25%.
a. If the cost of the part is $20 per unit, what is the economic order quantity?
b. Assume 250 days of operation per year. If the lead time for an order is 12 days) what is the reorder point?
c. If the lead time for the part is seven weeks (35 days), what is the reorder point?
d. What is the reorder point for part (c) if the reorder point is expressed in terms of the inventory on hand rather than the inventory position?
a. If the cost of the part is $20 per unit, what is the economic order quantity?
b. Assume 250 days of operation per year. If the lead time for an order is 12 days) what is the reorder point?
c. If the lead time for the part is seven weeks (35 days), what is the reorder point?
d. What is the reorder point for part (c) if the reorder point is expressed in terms of the inventory on hand rather than the inventory position?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
30
The Gilbert Air-Conditioning Company is considering the purchase of a special shipment of portable air conditioners manufactured in Japan. Each unit will cost Gilbert $80, and it will be sold for $125. Gilbert does not want to carry surplus air conditioners over until the following year. Thus, all surplus air conditioners will be sold to a wholesaler for $50 per unit. Assume that the air conditioner demand follows a normal probability distribution with ? = 20 and ? = 8.
a. What is the recommended order quantity?
b. What is the probability that Gilbert will sell all units it orders?
a. What is the recommended order quantity?
b. What is the probability that Gilbert will sell all units it orders?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
31
All-Star Bat Manufacturing, Inc., supplies baseball bats to major and minor league baseball teams. After an initial order in January, demand over the six-month baseball season is approximately constant at 1000 bats per month. Assuming that the bat production process can handle up to 4000 bats per month, the bat production setup costs are $150 per setup, the production cost is $10 per bat, and the holding costs have a monthly rate of 2%, what production lot size would you recommend to meet the demand during the baseball season? If All-Star operates 20 days per month, how often will the production process operate, and what is the length of a production run?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
32
The Bridgeport city manager and the chief of police agreed on the size of the police force necessary for normal daily operations. However, they need assistance in determining the number of additional police officers needed to cover daily absences due to injuries, sickness, vacations, and personal leave. Records over the past three years show that the daily demand for additional police officers is normally distributed with a mean of 50 officers and a standard deviation of 10 officers. The cost of an additional police officer is based on the average pay rate of $150 per day. If the daily demand for additional police officers exceeds the number of additional officers available, the excess demand will be covered by overtime at the pay rate of $240 per day for each overtime officer.
a. If the number of additional police officers available is greater than demand, the city will have to pay for more additional police officers than needed. What is the cost of overestimating demand?
b. If the number of additional police officers available is less than demand, the city will have to use overtime to meet the demand. What is the cost of underestimating demand?
c. What is the optimal number of additional police officers that should be included in the police force?
d. On a typical day, what is the probability that overtime will be necessary?
a. If the number of additional police officers available is greater than demand, the city will have to pay for more additional police officers than needed. What is the cost of overestimating demand?
b. If the number of additional police officers available is less than demand, the city will have to use overtime to meet the demand. What is the cost of underestimating demand?
c. What is the optimal number of additional police officers that should be included in the police force?
d. On a typical day, what is the probability that overtime will be necessary?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
33
Assume that a production line operates such that the production lot size model of Section 10.2 is applicable. Given D = 6400 units per year, C o = $100, and C o = $2 per unit per year, compute the minimum cost production lot size for each of the following production rate:
a. 8000 units per year
b. 10,000 units per year
c. 32,000 units per year
d. 100,000 units per year
Compare the EOQ recommended lot size using equation (10.5). What two observations can you make about relationship between the EOQ model and the production lot size model?
a. 8000 units per year
b. 10,000 units per year
c. 32,000 units per year
d. 100,000 units per year
Compare the EOQ recommended lot size using equation (10.5). What two observations can you make about relationship between the EOQ model and the production lot size model?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
34
A perishable dairy product is ordered daily at a particular supermarket. The product, which costs $1.19 per unit, sells for $1.65 per unit. If units are unsold at the end of the day, the supplier takes them back at a rebate of $1 per unit. Assume that daily demand is approximately normally distributed with ? = 150 and ? = 30.
a. What is your recommended daily order quantity for the supermarket?
b. What is the probability that the supermarket will sell all the units it orders?
c. In problems such as these, why would the supplier offer a rebate as high as $1? For example, why not offer a nominal rebate of, say, 25¢ per unit? What happens to the supermarket order quantity as the rebate is reduced?
a. What is your recommended daily order quantity for the supermarket?
b. What is the probability that the supermarket will sell all the units it orders?
c. In problems such as these, why would the supplier offer a rebate as high as $1? For example, why not offer a nominal rebate of, say, 25¢ per unit? What happens to the supermarket order quantity as the rebate is reduced?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
35
Assume that you are reviewing the production lot size decision associated with a production operation where P = 8000 units per year, D = 2000 units per year. C o = $300, and C h = $1.60 per unit per year. Also assume that current practice calls for production runs of 500 units every three months. Would you recommend changing the current production lot size? Why or why not? How much could be saved by converting to your production lot size recommendation?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
36
A retail outlet sells a seasonal product for $10 per unit. The cost of the product is $8 per unit. All units not sold during the regular season are sold for half the retail price in an end-of-season clearance sale. Assume that demand for the product is uniformly distributed between 200 and 800.
a. What is the recommended order quantity?
b. What is the probability that at least some customers will ask to purchase the product after the outlet is sold out? That is, what is the probability of a stockout using your order quantity in part (a)?
c. To keep customers happy and returning to the store later, the owner feels that stockouts should be avoided if at all possible. What is your recommended order quantity if the owner is willing to tolerate a 0.15 probability of a stockout?
d. Using your answer to part (c), what is the goodwill cost you are assigning to a stockout?
a. What is the recommended order quantity?
b. What is the probability that at least some customers will ask to purchase the product after the outlet is sold out? That is, what is the probability of a stockout using your order quantity in part (a)?
c. To keep customers happy and returning to the store later, the owner feels that stockouts should be avoided if at all possible. What is your recommended order quantity if the owner is willing to tolerate a 0.15 probability of a stockout?
d. Using your answer to part (c), what is the goodwill cost you are assigning to a stockout?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
37
Wilson Publishing Company produces books for the retail market. Demand for a current book is excepted to occur at a constant annual rate of 7200 copies. The cost of one copy of is $ 14.50. The holding cost is based on an 18% annual rate, and production setup costs are $ 150 per setup. The equipment on which the book is produced has an annual production volume of 25,000 copies. Wilson has 250 working days per year, and the lead time or a production run is 15 days. Use the production lot size model to compute the following values:
a. Minimum cost production lot size
b. Number of production runs per year
c. Cycle time
d. Length of a production run
e. Maximum inventory
f. Total annual cost
g. Reorder point
a. Minimum cost production lot size
b. Number of production runs per year
c. Cycle time
d. Length of a production run
e. Maximum inventory
f. Total annual cost
g. Reorder point

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck
38
Floyd Distributors, Inc., provides a variety of auto parts to small local garages. Floyd purchases parts from manufacturers according to the EOQ model and then ships the parts from a regional warehouse direct to its customers. For a particular type of muffler, Floyd's EOQ analysis recommends orders with Q * = 25 to satisfy an annual demand of 200 mufflers. Floyd's has 250 working days per year, and the lead time averages 15 days.
a. What is the reorder point if Floyd assumes a constant demand rate?
b. Suppose that an analysis of Floyd's muffler demand shows that the lead-time demand follows a normal probability distribution with ? = 12 and ? = 2.5. If Floyd's management can tolerate one stockout per year, what is the revised reorder point?
c. What is the safety stock for part (b)? If C h = $5/unit/year, what is the extra cost due to the uncertainty of demand?
a. What is the reorder point if Floyd assumes a constant demand rate?
b. Suppose that an analysis of Floyd's muffler demand shows that the lead-time demand follows a normal probability distribution with ? = 12 and ? = 2.5. If Floyd's management can tolerate one stockout per year, what is the revised reorder point?
c. What is the safety stock for part (b)? If C h = $5/unit/year, what is the extra cost due to the uncertainty of demand?

Unlock Deck
Unlock for access to all 38 flashcards in this deck.
Unlock Deck
k this deck


