Deck 4: The Meaning of Interest Rates
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 4: The Meaning of Interest Rates
1
Calculate the present value of a $1,000 discount bond with five years to maturity if the yield to maturity is 6%.
To find the present value of a future payment, we must discount that payment by the current interest rate. "Discounting" means to calculate the value of this payment in the future back in today's dollars, since we know that a dollar today is worth more than a dollar tomorrow because we are able to invest that dollar to generate returns in the future that exceed a dollar.
Suppose the yield to maturity is 6% and a $1,000 discount bond has 5 years to maturity. The formula to find the present value of this discount bond is given as: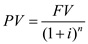 , where PV is the present value of this discount bond, i is the yield to maturity, n is the time to maturity, and FV is the face value of the discount bond.
, where PV is the present value of this discount bond, i is the yield to maturity, n is the time to maturity, and FV is the face value of the discount bond.
Using the above formula, the present value of this discount bond is calculated as follows: The present value of this discount bond is
The present value of this discount bond is 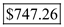 .
.
Suppose the yield to maturity is 6% and a $1,000 discount bond has 5 years to maturity. The formula to find the present value of this discount bond is given as:
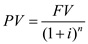 , where PV is the present value of this discount bond, i is the yield to maturity, n is the time to maturity, and FV is the face value of the discount bond.
, where PV is the present value of this discount bond, i is the yield to maturity, n is the time to maturity, and FV is the face value of the discount bond.Using the above formula, the present value of this discount bond is calculated as follows:
 The present value of this discount bond is
The present value of this discount bond is 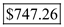 .
. 2
A lottery claims its grand prize is $10 million, payable over 5 years at $2,000,000 per year. If the first payment is made immediately, what is this grand prize really worth? Use an interest rate of 6%.
To find the present value of a stream of cash flows, we must discount each year's payment by the current interest rate. "Discounting," means to calculate the value of a future cash flow back in today's dollars, since we know that a dollar today is worth more than a dollar tomorrow because we are able to invest that dollar to generate returns in the future that exceed a dollar.
Suppose the interest rate today is 6% and a lottery grand prize pays $2,000,000 each year for 5 years. The formula to discount this future stream of cash flows is given as: , where PV is the present value of this stream of payments, i is the interest rate today, and P n is the payment in time n ; P 0 is the payment made today.
, where PV is the present value of this stream of payments, i is the interest rate today, and P n is the payment in time n ; P 0 is the payment made today.
Using the above formula, the present value of this stream of payments from the lottery grand prize is calculated as follows: This grand prize of $10,000,000 is really worth only
This grand prize of $10,000,000 is really worth only 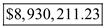 .
.
Suppose the interest rate today is 6% and a lottery grand prize pays $2,000,000 each year for 5 years. The formula to discount this future stream of cash flows is given as:
 , where PV is the present value of this stream of payments, i is the interest rate today, and P n is the payment in time n ; P 0 is the payment made today.
, where PV is the present value of this stream of payments, i is the interest rate today, and P n is the payment in time n ; P 0 is the payment made today.Using the above formula, the present value of this stream of payments from the lottery grand prize is calculated as follows:
 This grand prize of $10,000,000 is really worth only
This grand prize of $10,000,000 is really worth only 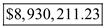 .
. 3
Would a dollar tomorrow be worth more to you today when the interest rate iS₂0% or when it iS₁0%?
Calculate present worth of dollar, when the interest rate iS₂0%:
Formula of present worth: Where,
Where,
Present worth is represented as PW ,
Future worth is represented as FW ,
Interest rate is represented as i.
Calculate present worth: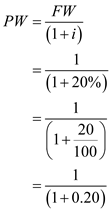
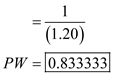 Therefore, present worth of dollar, when the interest rate iS₂0% is 0.83.
Therefore, present worth of dollar, when the interest rate iS₂0% is 0.83.
Calculate present worth of dollar, when the interest rate iS₁0%:
Calculate present worth:
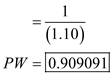 Therefore, present worth of dollar, when the interest rate iS₁0% is 0.91.
Therefore, present worth of dollar, when the interest rate iS₁0% is 0.91.
Thus, this shows that 10% interest rate has a higher value.
Formula of present worth:
 Where,
Where,Present worth is represented as PW ,
Future worth is represented as FW ,
Interest rate is represented as i.
Calculate present worth:
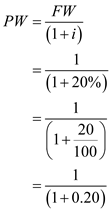
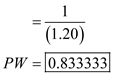 Therefore, present worth of dollar, when the interest rate iS₂0% is 0.83.
Therefore, present worth of dollar, when the interest rate iS₂0% is 0.83.Calculate present worth of dollar, when the interest rate iS₁0%:
Calculate present worth:

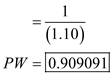 Therefore, present worth of dollar, when the interest rate iS₁0% is 0.91.
Therefore, present worth of dollar, when the interest rate iS₁0% is 0.91.Thus, this shows that 10% interest rate has a higher value.
4
What is the yield to maturity on a $ 1,000-face-value discount bond maturing in one year that sells for $800?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
In this chapter, we discussed long-term bonds as if there were only one type, coupon bonds. In fact, investors can also purchase long-term discount bonds. A discount bond is sold at a low price, and the whole return comes in the form of a price appreciation. You can easily compute the current price of a discount bond by using the financial calculator at http://www.treasurydirect.gov/indiv/tools/tools_savingsbondcalc.htm.
To compute the values for savings bonds, read the instructions on the page and click on Get Started. Fill in the information (you do not need to fill in the Bond Serial Number field) and click on Calculate.
To compute the values for savings bonds, read the instructions on the page and click on Get Started. Fill in the information (you do not need to fill in the Bond Serial Number field) and click on Calculate.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
What is the yield to maturity on a simple loan for $1 million that requires a repayment of $2 million in five years' time?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Write down the formula that is used to calculate the yield to maturity on a 20-year 10% coupon bond with $1,000 face value that sells for $2,000.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Which $1,000 bond has the higher yield to maturity, a twenty-year bond selling for $800 with a current yield of 15% or a one-year bond selling for $800 with a current yield of 5%?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
To help pay for college, you have just taken out a $1,000 government loan that makes you pay $126 per year for 25 years. However, you don't have to start making these payments until you graduate from college two years from now. Why is the yield to maturity necessarily less than 12%? (This is the yield to maturity on a normal $1,000 fixed-payment loan on which you pay $126 per year for 25 years.)

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
Consider a bond with a 4% annual coupon and a face value of $1,000. Complete the following table. What relationships do you observe between years to maturity, yield to maturity, and the current price? 


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
A financial adviser has just given you the following advice: "Long-term bonds are a great investment because their interest rate is over 20%." Is the financial adviser necessarily right?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
Consider a coupon bond that has a $1,000 par value and a coupon rate of 10%. The bond is currently selling for $1,044.89 and has two years to maturity. What is the bond's yield to maturity?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
If mortgage rates rise from 5% to 10% but the expected rate of increase in housing prices rises from 2% to 9%, are people more or less likely to buy houses?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
What is the price of a perpetuity that has a coupon of $50 per year and a yield to maturity of 2.5%? If the yield to maturity doubles, what will happen to the perpetuity's price?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
When is the current yield a good approximation of the yield to maturity?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Property taxes in a particular district are 4% of the purchase price of a home every year. If you just purchased a $250,000 home, what is the present value of all the future property tax payments? Assume that the house remains worth $250,000 forever, property tax rates never change, and a 6% interest rate is used for discounting.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Why would a government choose to issue a perpetuity, which requires payments forever, instead of a terminal loan, such as a fixed-payment loan, discount bond, or coupon bond?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
A $1000-face-value bond has a 10% coupon rate, its current price is $960, and its price is expected to increase to $980 next year. Calculate the current yield, the expected rate of capital gain, and the expected rate of return.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
Under what conditions will a discount bond have a negative nominal interest rate? Is it possible for a coupon bond or a perpetuity to have a negative nominal interest rate?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Assume you just deposited $1,000 into a bank account. The current real interest rate iS₂%, and inflation is expected to be 6% over the next year. What nominal rate would you require from the bank over the next year? How much money will you have at the end of one year? If you are saving to buy a fancy bicycle that currently sells for $1,050, will you have enough money to buy it?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
With a discount bond, the return on the bond is equal to the rate of capital gain.

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
If there is a decline in interest rates, which would you rather be holding, long-term bonds or short-term bonds? Why? Which type of bond has the greater interest-rate risk?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Interest rates were lower in the mid-1980s than in the late 1970s, yet many economists have commented that real interest rates were actually much higher in the mid-1980s than in the late 1970s. Does this make sense? Do you think that these economists are right?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Retired persons often have much of their wealth placed in savings accounts and other interest-bearing investments, and complain whenever interest rates are low. Do they have a valid complaint?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
If the interest rate iS₁0%, what is the present value of a security that pays you $1,100 next year, $1,210 the year after, and $1,331 the year after that?

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck


